Laboratorio di Didattica di elaborazione dati – 4B
IL TEOREMA LIMITE CENTRALE E LA DISTRIBUZIONE NORMALE
Ora ci occupiamo per un attimo con il teorema limite centrale. La sua formulazione è la seguente:
Sia Sn una variabile aleatoria somma di n variabili aleatorie indipendenti Xi aventi ciascuna la
stessa distribuzione di probabilità, speranza matematica μ e varianza σ2; al crescere di n, Sn tende
ad assumere una distribuzione normale con media nμ e varianza nσ2.
1. Lanciamo un dado 30 volte, sommando i resultati. Qual è la probabilità di ottenere una
somma tra 100 e 110 (inclusivo)?
Usando i risultati dell'esercizio 4A, calcola la speranza matematica e la deviazione standard per un
singolo lancio (ci sino solo sei valori possibili...). Poi, usando il teorema limite centrale calcola la
speranza matematica della somma di 30 lanci e la sua deviazione standard. Passa alla distribuzione
N(0, 1) è calcola la probabilità. Io ho ottenuto 40.70%. A dire la verità, questo risultato è solo quasi
credibile. La causa vedremo in un attimo. Prima, facciamo una simulazione. Come hai già fatto
nell'esercizio 2, genera un campione dei 30 lanci del dado, nelle colonne seguenti, nella stessa riga.
Nella colonna precedente (o seguente, come vuoi) calcola la somma. Incolla la stessa riga 1000 volte
(nelle righe seguenti). Abbiamo ottenuto 1000 risultati (somme) di un esperimento numerico.
Ricorda come possiamo contare il numero dei valori compresi fra 100 e 110 (inclusivo!, usa <= e
>=), utilizzando la funzione SE() (non CONTA.SE()!) e una formula in modalità array (formula in
forma di matrice). Se non ricordi, vedi il primo esercizio. Conta i numeri. Se la probabilità calcolata
appena è credibile, ci aspettiamo più o meno 407 valori compresi fra 100 e 110. Puoi ripetere il
nostro esperimento premendo F9.
Credo che il risultato di un esperimento non sia d'accordo con la probabilità calcolata. La causa è la
seguente. La distribuzione normale è una distribuzione continua, mentre la somma dei valori discreti
segue una distribuzione discrete. Quando si vuole aprossimare una distribuzione discrete con un una
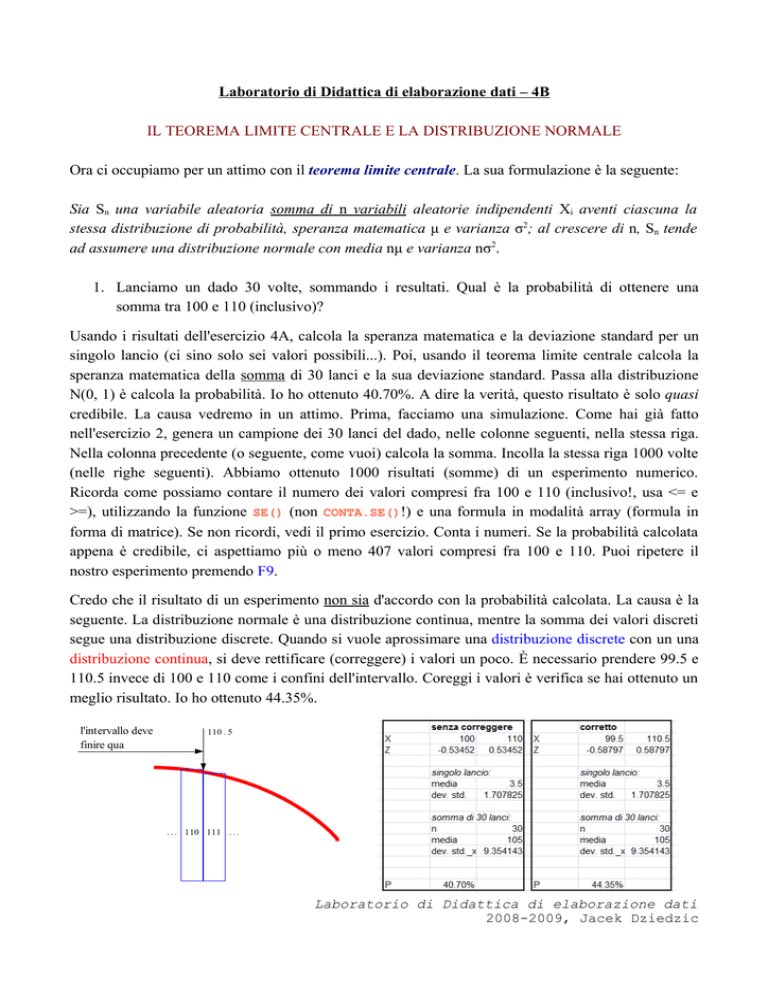
distribuzione continua, si deve rettificare (correggere) i valori un poco. È necessario prendere 99.5 e
110.5 invece di 100 e 110 come i confini dell'intervallo. Coreggi i valori è verifica se hai ottenuto un
meglio risultato. Io ho ottenuto 44.35%.
l'intervallo deve
finire qua
110 . 5
. . . 110 111 . . .
Laboratorio di Didattica di elaborazione dati
2008-2009, Jacek Dziedzic
2. Una scatola contiene 50 pastiglie. Il peso di ciascuna pastiglia è una variabile con un valor
medio 1.2 gr e varianza 0.09 gr. Usando il teorema limite centrale, determina la probabilità
che la scatola abbia un peso netto
a) superiore a 62 gr;
b) inferiore a 59 gr;
c) compreso tra 56 e 64 gr.
L'approsimazione di continuità non la dobbiamo usare qua – il peso è un valore continuo.
Io ho ottenuto: a) 17.29%; b) 31.87%; c) 94.07%.
3. Si lancia 10 volte una moneta. Determina la probabilità che si presenti un numero di teste
minore di 4. Verifica se si deve usare l'approsimazione di continuità. Finalmente calcola la
stessa probabilità usando la distribuzione di Bernoulli.
4. Se senti ambizioso (e vuoi finire tra poco), cerca di ripetere l'esercizio con i condensatori (del
laboratorio precedente), ma per campioni di tre condensatori. L'unica difficoltà sarebbe
generare tre colonne con numeri ordinali di capacità (da 1 1 1 a 4 4 4), ma se capisci bene la
funzione SE(), ci riuscirai. Verifica che abbia ottenuto x =
.
3
Laboratorio di Didattica di elaborazione dati
2008-2009, Jacek Dziedzic











