Il Modello a 4 Spaziotempi della Realtà

Il Modello a 4 Spaziotempi della Realtà
Giorgio Fontana
University of Trento, I-38050 Povo, Italy
+39-0461-883906; [email protected]
Abstract. Noi viviamo in uno spaziotempo 3+1 che è inteso come una descrizione dell’universo con tre dimensioni
spazio ed una dimensione tempo. La dimensionalità dello spaziotempo sembra così naturale da essere raramente
criticata. Gli esperimenti e le teorie relativistiche ci insegnano che ci sono quattro dimensioni fondamentali, tra queste
il tempo è trattato come una dimensione speciale. La specialità del tempo può essere rimossa, per arrivare al concetto
che il tempo è semplicemente una funzione di quattro nuove dimensioni fondamentali, che hanno ora proprietà
identiche, in combinazione con l’invarianza di Lorentz. Si deduce quindi un modello nel quale un quadrispazio,
caratterizzato da quattro coordinate spaziali, può ospitare quattro “equivalenti ed ortogonali” spaziotempi, ciascuno con
tre coordinate spaziali ed una coordinata temporale. Le coordinate sono condivise; perciò il quadrispazio ed i quattro
spaziotempi sono tutti in uno. L’interazione elettromagnetica è confinata in ciascuno spaziotempo ed il ruolo della
velocità della luce sembra essere quello di barriera per l’interazione elettromagnetica. Il moto degli oggetti può essere
descritto da un’ottica quadridimensionale nel quadrispazio. Ciascuno dei quattro spaziotempi può ospitare un universo
e, in accordo con le recenti osservazioni, il modello proposto può essere direttamente applicato a problemi quali
l’asimmetria cosmologica tra materia ed antimateria e la natura della materia oscura. Anche i viaggi spaziali possono
trarre beneficio dai concetti presentati.
INTRODUZIONE
Uno dei misteri irrisolti che la scienza sta affrontando e cercando di risolvere è l’origine dell’asimmetria materiaantimateria (Dine, 2004), nonostante il più semplice modello di origine dell’universo sia a favore di una perfetta
simmetria, osservata negli esperimenti con gli acceleratori.
Il mistero dell’antimateria non è il solo. L’osservazione dell’universo locale e profondo con ogni possibile strumento
ottico mostra solamente la presenza di vuoto, radiazione elettromagnetica e materia, più precisamente materia
barionica (che consiste di fermioni, quali i protoni, neutroni, elettroni).
Tenendo in considerazione i fenomeni gravitazionali, è stata fatta una scoperta difficile da spiegare. La materia
barionica è solamente il 5% della densità di energia totale dell’universo , meno di ¼ è un qualche tipo di materia non
barionica, e ¾ è in una forma di pressione negativa, chiamata costante cosmologica (Peebles, 2003; Deffayet, 2002).
La materia oscura sembra composta da un qualche tipo di oggetti invisibili di dimensione sconosciuta, che hanno
massa ma restano diluiti e non si accumulano gravitazionalmente a formare stelle o pianeti. Questi oggetti di fatto si
accumulano su scala galattica, dove è stata dedotta la loro esistenza; essi potrebbero anche indurre la formazione
delle stesse galassie. Come può accadere tutto ciò? Essendo la materia non barionica qui tra noi, perché non
possiamo vederla, ne direttamente, ne mediante un insieme di sensori già costruiti, ne mediante effetti di eclisse su
scala galattica? Perché l’esatta natura della materia non barionica non è gia prevista da un modello delle particelle
che è sostanzialmente assai accurato? Esiste realmente nel “nostro” universo locale/visibile ? Potrebbe la
comprensione del problema della materia oscura portare ad un corretto approccio al problema della costante
cosmologica o divenire la base della meccanica quantistica?
CP746, Space Technology and Applications International Forum—STAIF 2005, edited by M. S. El-Genk
© 2005 American Institute of Physics 0-7354-0230-2/05/$22.50
1
Il nuovo paradigma considerato è che la materia barionica “visibile” è un fenomeno che accade nello spaziotempo in
cui noi viviamo, dove “vivere” significa “produrre fenomeni elettromagnetici”. Al contrario, la materia oscura
popola uno o più universi paralleli che condividono una o più dimensioni spaziotemporali con il “nostro” universo
locale, che è racchiuso dal nostro spaziotempo locale. La materia oscura è perciò materia visibile nel “suo” universo
locale. Anche la gravità secondo Einstein (Misner, 1973) può collegare gli spaziotempi paralleli. Infatti la curvatura
in un dato spaziotempo può essere osservata dai differenti universi paralleli che condividono la stessa dimensione e
la totalità degli universi paralleli forma ciò che da ora in poi considereremo l’intero universo, o più semplicemente,
l’universo. Se l’intero universo contiene la sovrapposizione di un certo numero di spaziotempi differenti che sono
elettromagneticamente ortogonali, cioè spaziotempi in cui l’interazione elettromagnetica è confinata nel proprio
spaziotempo, allora c’è più “spazio” per differenti forme di materia, che potrebbero essere reciprocamente
“incompatibili” se mescolate direttamente. L’antimateria potrebbe essere confinata in un universo parallelo, e lo
stesso potrebbe verificarsi per altre forme di particelle con massa. In accordo con le misure del rapporto di massa tra
la materia visibile e quella oscura ottenuto dalle osservazioni della dinamica di una vasto campione di galassie, è una
ragionevole ipotesi che la materia barionica sia circa 1/5 della massa totale dell’intero universo materiale. Il
problema della materia oscura è perciò risolto dalla possibile esistenza di quattro o cinque universi paralleli,
ciascuno con circa la stessa massa totale. Spaziotempi con dimensionalità più elevata sono spesso studiati in fisica
teorica; essi appaiono nella teoria di Kaluza-Klein, nella teoria delle stringhe e nelle brane theories. In molte teorie
le dimensioni aggiuntive sono arrotolate a dimensioni dell’ordine della lunghezza di Planck e perciò inaccessibili
all’osservazione diretta. Nella teoria delle Brane (Germani, 2002) sono spesso predette dimensioni aggiuntive
macroscopiche, ma gli esperimenti condotti fino ad ora non hanno confermato la reale esistenza di “grandi”
dimensioni aggiuntive oltre alle solite quattro. Per mantenere pieno accordo con questi fatti e con la ben nota
Relatività Speciale, il modello proposto in questo lavoro cambia la nostra visione della realtà dando al “tempo” il
ruolo secondario di coordinata derivata da altre più fondamentali. Il numero complessivo di grandi dimensioni
fondamentali è ancora uguale alle quattro osservate, che ora hanno tutte le proprietà di dimensioni di spazio.
DEDUZIONE DEL MODELLO
Il modello proposto è stato studiato per la prima volta dell’autore cercando di scrivere la funzione d’onda di
gravitoni in spaziotempi con una costante cosmologica. Imponendo l’unitarietà della funzione d’onda (la proprietà
che definisce pari a uno la probabilità di trovare la particella in uno spaziotempo) sotto tutte le possibili condizioni
energetiche porta a dedurre la possibile esistenza di un iperspazio con quattro dimensioni spazio, che perciò viene
chiamato quadrispazio. La possibilità che la costante cosmologica dipenda dalle coordinate (Modanese, 2004), in
modo da riportare il gravitone indietro in uno spazitempo 3+1, apre la possibilità di scelta tra quattro spaziotempi
con tre dimensioni spazio ed una di tempo, perciò dovrebbero esistere quattro spaziotempi 3+1. Noi certamente
viviamo in uno di questi spaziotempi 3+1; si possono poi formulare ipotesi sul ruolo ed il contenuto dei rimenenti
tre spaziotempi, ed esperimenti potranno discriminare tra queste. Per mostrare indipendentemente che esistono
quattro spaziotempi 3+1 è necessario capire cos’è uno spaziotempo 3+1 e, più specificamente, quale sia la differenza
tra “spazio” e “tempo”. Sfortunatamente questo non è semplice. In Relatività Generale (GR) (Misner, 1973) la
differenze tra spazio e tempo è codificata nel segno + o – della metrica. E’ compito nostro definire il problema.
Si deve alla Relatività Speciale la prima chiara differenziazione teorica tra spazio e tempo. La differenza è legata
alla costanza della velocità della luce ed alla sua invarianza per tutti gli osservatori (l’invarianza di Lorentz), che è
un fatto sperimentale. Ed è anche un fatto sperimentale il fatto che il numero delle grandi dimensioni spazio sia tre,
ed a questo numero le teorie si devo adattare. E’ lo scopo di questo articolo proporre che la realtà può essere
differente. Se la differenza tra spazio e tempo è modellizzata dall’invarianza di Lorentz, una formulazione differente
ma equivalente della Relatività Speciale può fornire qualche indicazione. Infatti il concetto di trattare lo spazio ed il
tempo allo stesso modo è lo scopo della Relatività Speciale Euclidea (ESR). La metrica dello spaziotempo piatto in
ESR ha la segnatura ++++, perciò il nostro spaziotempo 3+1 è descritto racchiuso nel quadrispazio. Una visione più
approfondita della ESR farà emergere con facilità i quattro spaziotempi, e riconoscere questa possibilità è uno dei
contributi dati da questo articolo.
CP746, Space Technology and Applications International Forum—STAIF 2005, edited by M. S. El-Genk
© 2005 American Institute of Physics 0-7354-0230-2/05/$22.50
2
LA RELATIVITA` SPECIALE EUCLIDEA
Storicamente la Relatività Speciale Euclidea venne prima proposta da Montanus (2001) e poi successivamente
sviluppata da Gersten (2003). Almeida (2001) ha recentemente e indipendentemente sviluppato gli stessi concetti,
derivando una teoria chiamata ottica quadridimensionale “4-dimensional optics” (4DO). Gersten ed Almeida hanno
riconosciuto che la teoria è un’estensione dell’ottica geometrica e dell’ottica delle onde. Recentemente Almeida
(2004b) ha fatto l’interessante tentativo di costruire una teoria 4DO della gravitazione.
La Relatività Speciale (SR) venne sviluppata per descrivere matematicamente l’osservazione che la velocità della
luce è la stessa per tutti gli osservatori. Questo fatto ha portato all’abbandono della trasformazione di Galileo in
favore di quella di Lorentz. Divenne allora ovvio che spazio e tempo erano entrambi parte di una singola entità
chiamata “spaziotempo”, del quale la SR prediceva le rilevanti proprietà della dilatazione temporale ed incremento
della massa. Questi effetti sono confermati da molti esperimenti. Nonostante il suo successo, SR è spesso affetta da
ambiguità di interpretazione dei risultati. In SR, la grandezza:
(dτ )2 = c 2 (dt )2 − (dx )2 − (dy )2 − (dz )2 ,
(1)
con c uguale alla velocità della luce, è invariante rispetto ad una trasformazione di Lorentz. Minkowski propose di
considerare t, x, y, e z come le coordinate dello spaziotempo, essendo poi τ una misura della distanza, chiamata
tempo proprio. L’equazione (1) è la metrica dello spaziotempo piatto; essa è una descrizione “locale” delle
proprietà dello spaziotempo in assenza di gravità. In ESR l’equazione (1) è riscritta e discussa:
2
2
2
2
2
c 2 (dt ) = (dτ ) + (dx ) + (dy ) + (dz ) .
(2)
Nell’equazione (2) τ, x, y e z sono le coordinate del quadrispazio e t è il parametro usato per valutare la velocità e
l’accelerazione; sostanzialmente l’equazione (2) è la definizione del tempo. Il tempo t è una funzione integrale
locale dei cambiamenti delle quattro coordinate del quadrispazio, dimensionalmente allineate da c. Il tempo t esiste
se c’è movimento nel quadrispazio, e in ESR un orologio è perciò comparabile ad un contachilometri per viaggi nel
quadrispazio. In ESR la misurabilità del tempo t, che è una funzione di τ, x, y e z, implica l’esistenza di una
interazione tra lo strumento di misura e l’ambiente. La trasformazione di Lorentz viene poi descritta da una
rotazione nel gruppo SO(4) (Gersten, 2003).
Nella presente interpretazione della ESR le grandezze che appaiono a destra dell’uguale nell’equazione (2) sono
omogenee ed hanno la dimensione di coordinate spazio. Con τ coordinata spazio, è certamente possibile esplorare
questa coordinata con qualche metodo tecnologico. Per scoprirlo osserviamo che nello spazio piatto Euclideo c’è un
invariante , il quadrato della quadrivelocità, ottenuto dall’equazione (2) dividendo per (dt)2:
2
2
2
2
 dτ   dx   dy   dz 
  +   +   +   = c2 .
 dt   dt   dt   dt 
(3)
In ESR c’è un singolo quadrispazio in cui tutte le particelle, per le quali vale la trasformazione di Lorentz, viaggiano
alla velocità della luce. Gersten ha infatti riconosciuto che l’equazione (3) è una restrizione nel quadrispazio cioè
essa definisce un sottospazio in cui la trasformazione di Lorentz può avvenire per una particella. Prendendo il
Lagrangiano per una particella libera in ESR (Montanus, 2001):
 dτ  2  dx  2  dy  2  dz  2
L = m   +   +   +    = mc 2 ,
 dt   dt   dt   dt  
(4)
essendo L=K-U, energia cinetica meno energia potenziale, abbiamo per una particella libera con massa E=mc2.
L’espressione è semplice perché in ESR (in assenza di gravità) la massa non dipende dalla velocità e la velocità è
una costante universale: E è una costante del moto. Poiché E ∝ m, E può essere facilmente interpretata come
l’energia richiesta per “lanciare” letteralmente una particella nell’esistenza. Per particelle con velocità nel trispazio
uguale a zero, è il primo termine a sinistra nell’equazione (3) che è uguale al quadrato della velocità della luce. E lo
stesso si applica alle altre tre possibilità in cui particelle viaggiano a bassa velocità (rispetto a c) nei trispazi (τ , x, y),
CP746, Space Technology and Applications International Forum—STAIF 2005, edited by M. S. El-Genk
© 2005 American Institute of Physics 0-7354-0230-2/05/$22.50
3
(τ , x, z) and (τ , y, z). E’ solamente necessario mostrare che i fotoni viaggiano solamente in un trispazio per
concludere che possono esistere nel quadrispazio quattro insiemi di particelle (universi locali ai quali si applica
l’invarianza di Lorentz) elettromagneticamente ortogonali (cioè reciprocamente invisibili per osservatori fermi in
ciascuno di essi). L’esistenza di quattro insiemi ortogonali di particelle, che possiamo considerare ospitati da quattro
spaziotempi, è motivata dal principio di simmetria: tutte le dimensioni spazio hanno proprietà identiche, esattamente
come suggerisce l’equazione (2). Gli universi locali viaggiano alla velocità della luce lungo le quattro coordinate
ortogonali di un sistema di riferimento in cui “direzione” e “velocità” sono univocamente definite. Dentro ciascun
universo locale, la SR mantiene la sua validità.
I fotoni viaggiano solo in un trispazio perché per i fotoni in un universo locale, per esempio in (x, y, z), abbiamo:
2
2
2
 dx   dy   dz 
  +   +   = c2 ,
 dt   dt   dt 
(5)
che rappresenta la costanza della velocità della luce. Perciò considerando gli stessi fotoni in un quadrispazio
abbiamo:
2
 dτ 
  = 0.
 dt 
(6)
Questi fotoni non possono viaggiare lungo la coordinata spazio τ, mentre il rispettivo universo materiale corre via
lungo τ con velocità c. Lo stesso si applica ai rimanenti tre spaziotempi. Quando la materia incrementa la sua
velocità in un trispazio e si avvicina alla velocità della luce, essa si sposta verso un altro universo parallelo, come
mostrato dall’equazione (3). Una nave spaziale che viaggia in un trispazio a circa metà della velocità della luce
dovrebbe essere in grado di osservare uno o più universi paralleli e in linea di principio essere in grado di
raggiungerli. Sembra inoltre abbastanza naturale attribuire lo stesso comportamento agli oggetti stellari che
osserviamo ai confini del nostro universo visibile, oggetti che sembrano cadere verso una frontiera indefinita.
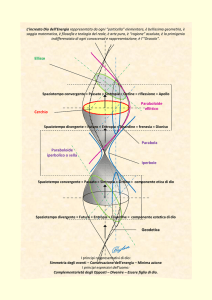
FIGURE 1. Rappresentazione Locale dei Quattro Spaziotempi 3+1.
La figura (1) rappresenta i quattro spaziotempi in un quadrispazio localmente euclideo. Particelle che sono ferme
(nel loro proprio spaziotempo) viaggiano a velocità c lungo la loro coordinata “tempo proprio” del quadrispazio. Il
CP746, Space Technology and Applications International Forum—STAIF 2005, edited by M. S. El-Genk
© 2005 American Institute of Physics 0-7354-0230-2/05/$22.50
4
nostro spaziotempo è fatto simbolicamente di mattoni e consiste in un numero infinito (un continuum) di τ-frames,
alcuni sono mostrati come linee di contorno. La particella P può raggiungere un altro spaziotempo (P->P’) con
l’aiuto di una trasformazione di Lorentz, una rotazione SO4. Viaggiare tra τ-frames differenti richiede un
cambiamento locale della velocità della luce, che richiede un indice di rifrazione non unitario per la propagazione
delle particelle con massa, e l’effetto è prodotto dalla presenza di un campo gravitazionale.
L’ESR ha i propri paradossi, che sono differenti da quelli della SR. Per esempio, se io compio l’azione di accendere
una lampada, l’equazione (6) mostra che i fotoni emessi dalla lampada nel mio trispazio non raggiungeranno mai i
miei occhi. Infatti la mia velocità lungo la dimensione spaziale τ è c, e la velocità dei fotoni emessi lungo la
dimensione spaziale τ è zero. Perciò i fotoni viaggiano veramente nel trispazio, verso di me, a velocità c ma essi
raggiungeranno il mio “fantasma” in un τ-frame passato. La soluzione è che i fotoni che raggiungono i miei occhi
sono emessi in qualche τ-frame futuro, e la mia azione di accendere la lampada “sembra solamente” essere
puramente deliberata nel mio τ-frame presente. Il quadrispazio codifica passato, presente e futuro nelle sue quattro
dimensioni.
Per gli essere senzienti, come noi, tutta l’informazione è trasportata dai fotoni, questo fatto spiega perché noi
possiamo agire solo nel nostro presente. Noi siamo parte di un universo che “viaggia” nello spazio verso il futuro
lungo la coordinata τ, la nostra attività nel presente “elabora” il futuro che arriva e produce il passato lungo la
coordinata τ. Il fatto che noi vediamo fotoni arrivare dai futuri τ-frames e da distanze differenti nel trispazio, ci
insegna che c’è un numero infinito di τ-frames prima e dopo il nostro frame e che ciascun frame è il presente di
un’altra esistenza materiale. I τ-frames sono tutti vivi allo stesso modo: τ-frames passati e futuri sono reali come il
nostro presente nel quadrispazio, perciò è il quadrispazio che contiene l’informazione, la materia è solamente un
processo. L’impatto filosofico di questa interpretazione della ESR verrà discusso più avanti.
La causalità non è una proprietà generale del quadrispazio, perché non c’è un unico parametro temporale calcolabile
dall’equazione (2). La causalità è una proprietà di linee temporali non intersecanti (sequenze di τ frames), che sono
traiettorie non intersecanti seguite dalle particelle a cui è applicabile l’invarianza di Lorentz. In questo quadro, gli
universi locali seguono traiettorie rettilinee, libere da cicli nelle linee temporali.
PARTICELLE, FORZE E GRAVITAZIONE NEL QUADRISPAZIO.
La ESR è stata derivata dalla SR, perciò essa eredita una parziale verifica sperimentale dalla stessa SR. La 4DO, che
è una teoria della gravità nel quadrispazio, eredita una parziale verifica sperimentale dalla GR. Infatti è possibile
convertire le metriche della GR in indici di rifrazione ed entrambe le teorie possono dare risultati equivalenti o
comparabili (Almeida, 2004b; Montanus, 2001). Ovviamente l’interpretazione dei risultati è differente da quella
della GR. Nuovi esperimenti permetteranno quindi di discriminare tra i due differenti approcci.
Secondo Almeida (2001), nello spazio Euclideo è possibile scrivere:
2
c 2 (dt ) = g αβ d xα d x β ,
(7)
è gia stato dimostrato che in ESR il tensore metrico è:
g αβ = δ αβ .
(8)
Partendo dallo studio della propagazione dei fotoni dalle equazioni (5) e (6) otteniamo:
g 0α = g α 0 = 0, g ab = n 2 δ ab , ( a, b ≠ 0),
(9)
con n indice di rifrazione, funzione delle coordinate (n=1 senza gravità). Poi:
[
]
2
2
2
2
c 2 (dt ) = n 2 (dx ) + (dy ) + (dz ) ,
CP746, Space Technology and Applications International Forum—STAIF 2005, edited by M. S. El-Genk
© 2005 American Institute of Physics 0-7354-0230-2/05/$22.50
(10)
5
introducendo il principio variazionale:
δ ∫ ndσ = 0,
(11)
con
dσ =
(dx )2 + (dy )2 + (dz )2 ,
(12)
si ha il principio di Fermat della propagazione ottica. Perciò si può concludere che i fotoni viaggiano come onde con
velocità |c/n| e lunghezza d’onda λ=h/(|n|E). Più in generale, estendendo lo studio al quadrispazio, le equazioni (7),
(8) e (11) danno:
[
]
2
2
2
2
2
c 2 (dt ) = n 2 (dτ ) + (dx ) + (dy ) + (dz ) , n ≠ 0,
(13)
dopo essere passati in coordinate sferiche, con dϕ=0 e dθ=0, scrivendo ds2=n(dτ2) e sostituendo:
1  2Gm 
= 1 −
,
n 
r 
(14)
si può ottenere la metrica di Schwarzschild della Relatività Generale (Almeida, 2001). Un simile modello è stato
proposto da Montanus (2001), impiegando indici di rifrazione esponenziali, che sono in accordo con la GR usando
uno sviluppo in serie. E’ la possibilità di fare questi collegamenti tra 4DO e GR che da alla 4DO una possibilità di
soddisfare i vari test della GR, quelli che hanno gia passato la verifica sperimentale. L’interpretazione degli
esperimenti è ovviamente differente. Esperimenti futuri potranno mettere alla sbarra le due teorie.
L’indice di rifrazione descrive perciò le proprietà del quadrispazio, d’altro canto la sostituzione ds2=n(dτ2) indica
che con la presenza di materia e assumendo GR pienamente valida, l’indice di rifrazione non è isotropico, con
componenti che dipendono dalle quattro direzioni, ciò si può mostrare meglio con una trasformazione di coordinate
(d’Inverno, 1996) e con un calcolo rigoroso dei due indici di rifrazione (Almeida, 2004a). Le relazioni tra GR e 4DO
indicano che la gravità si propaga in quattro dimensioni, questo vale ovviamente anche per le onde gravitazionali
deboli, che viaggiano con velocità c (lontano da un campo gravitazionale) nel quadrispazio. L’indice di rifrazione
del quadrispazio appare come un quadrato nella metrica euclidea dell’equazione (13) e con |n|<1, cioè per Gm>r, la
velocità nel quadrispazio è più alta della velocità della luce. Infatti confrontando l’equazione (2) con l’equazione
(13) la velocità di tutte le particelle in un quadrispazio con indice di rifrazione, cioè in presenza di gravità è v=c/|n|.
In questa situazione la teoria euclidea è più facile da interpretare della Relatività Generale. La soluzione per le
traiettorie nel quadrispazio si ottiene applicando il principio di Fermat in quattro dimensioni, il nome 4DO nasce da
questo approccio.
Le particelle sono descritte da onde nel quadrispazio, perché tutte le particelle sono in movimento ad una qualche
velocità finita. Almeida (2001) ha suggerito di identificare queste onde con le onde di materia della Meccanica
Quantistica. L’equazione (7) ammette la soluzione in forma di onde parametrizzate lungo t:
& 2 = g αβ ∂α ∂ β Φ = δ αβ Φ.
Φ
(15)
Perciò delle onde appaiono non appena una direzione è definita, ed il processo è ovviamente una “lettura” nel
quadrispazio. Infatti, se l’indice di rifrazione del quadrispazio codifica un sequenza di informazioni, allora il moto
dell’onda/particella riproduce l’informazione codificata. D’altro canto la “lettura” influenza il quadrispazio come
nell’esempio dell’equazione (14), dove la massa di una particella associata ad un’onda modifica l’indice di
rifrazione del quadrispazio.
Combinando v=c/|n| con l’equazione (14) abbiamo:
 2Gm 
v = c 1 −
.
r 

CP746, Space Technology and Applications International Forum—STAIF 2005, edited by M. S. El-Genk
© 2005 American Institute of Physics 0-7354-0230-2/05/$22.50
(16)
6
Per piccole masse e grandi distanze, la presenza di una massa riduce la velocità locale della luce, che in accordo con
E=mc2 ed assumendo la conservazione dell’energia, cambia la massa locale di una seconda particella nel vicino
quadrispazio a m(c2/v2). Perciò la massa può divergere se la densità di massa va oltre un certo limite e l’energia è
conservata. Senza entrare in ulteriori dettagli sembra che la 4DO sia non lineare come la GR e perciò capace di
offrire molti ed interessanti sviluppi. Il sommarsi non lineare della massa può essere attribuito ad un effetto di
reazione positiva, nonostante il fatto che l’universo locale viaggi a velocità c lungo la sua quarta dimensione, infatti
la gravità si propaga in quattro dimensioni ed n non è soggetto a ritardi. I fotoni viaggiano in tre dimensioni ed un
loop di propagazione tra due fotoni in τ-frames differenti e in quattro dimensioni non è possibile:
l’elettromagnetismo è lineare.
L’ESR e la nozione di indice di rifrazione del quadrispazio sono una dipartita significativa dai concetti della
Relatività Generale: il quadrispazio è piatto, ha un indice di rifrazione, tutto ciò che non è indice di rifrazione è in
movimento e la velocità è una funzione dell’indice di rifrazione. Le forze sono associate a cambiamenti di traiettoria
delle particelle dovute all’indice di rifrazione.
Il concetto di forza in uno spaziotempo 3+1 inteso come proiezione di traiettorie nel quadrispazio suggerisce un
approccio al problema semplice ed unificato. Le differenti forze naturali, che obbediscono a regole differenti nello
spaziotempo 3+1, sono naturalmente associate a particelle differenti ed a proprietà differenti dell’indice di
rifrazione. Se una particella risponde a più di una forza, essa deve essere una particella composta. In piena analogia
con i materiali ottici, l’indice di rifrazione può essere una funzione della frequenza, permettendo perciò la creazione
di un modello 4DO di tutte le interazioni e spiegando le differenti intensità delle varie forze conosciute. Modulando
in frequenza la funzione d’onda di una particella (con vibrazioni a velocità relativistiche in un trispazio) si dovrebbe
poter modificare il suo spettro in frequenza e controllare l’intensità delle forze naturali. Per studiare le proprietà
dell’indice di rifrazione del quadrispazio si possono suggerire esperimenti molto simili a quelli pensati per studiare
le onde gravitazionali ad alta frequenza (HFGW) (Fontana, 2004 and 2003b; Baker, 2004).
Si è speculato sulla possibilità che l’universo possa essere una gigantesca simulazione (Bostrom, 2003). Dopo aver
familiarizzato con la ESR e la 4DO, si può essere tentati ad identificare l’indice di rifrazione con un dispositivo di
memoria nel quale le onde/particelle giocano il ruolo di segnali che fluiscono attraverso i circuiti quadridimensionali
dell’universo.
PROSPETTIVE PER I VIAGGI SPAZIALI E LA PROPULSIONE
La visione euclidea della dimensionalità può offrire una nuova prospettiva ai viaggi spaziali. Interazioni basate
sull’elettromagnetismo sono confinate nel trispazio e tutte le tecniche di propulsione note, eccetto una, sono legate
all’interazione elettromagnetica, spesso a livello molecolare o chimico. Con tre gradi di libertà, serve una grande
quantità di energia per dare energia cinetica ad un oggetto nel trispazio. Al contrario, le tecniche di propulsione
gravitazionale possono operare direttamente nel quadrispazio, ed un ben noto esempio di propulsione gravitazionale
e’ la cosiddetta “fionda gravitazionale”. Nel quadrispazio tutte le particelle viaggiano alla velocità della luce, perciò
la capacità di viaggiare può essere definita come la capacità di sterzare nel quadrispazio, che è la capacità di fare
trasformazioni di Lorentz. Infatti per la “fionda gravitazionale” non è richiesta alcuna propulsione, ma solo la
capacità di sterzare. Le onde gravitazionali ad alta frequenza (HFGW) sono state studiate in GR e possono essere
usate per una forma di “fionda gravitazionale artificiale” (Fontana, 2000 and 2003; Baker, 2004), e tecniche simili
possono essere interamente sviluppate in ESR and 4DO. I viaggi spaziali tra τ-frames differenti sembrano anche
possibili cambiando localmente l’indice di rifrazione e l’effetto è prodotto dalla presenza di un campo
gravitazionale.
Il quadrispazio non soffre delle distorsioni metriche della relatività Generale che portano ad una difficile
interpretazione e visualizzazione dei risultati in quella teoria. Nel quadrispazio la gravità è codificata dall’indice di
rifrazione e si può facilmente dimostrare che all’interno dell’orizzonte degli eventi di un buco nero di Schwarzschild
la quadrivelocità di ogni particella è maggiore della velocità della luce. Questo fatto non è associato a paradossi o
difficoltà concettuali. Sfortunatamente la controparte delle equazioni di Einstein per la 4DO non è stata ancora
scoperta, se non in alcuni semplici casi derivati dalla stessa Relatività Generale. E’ possibile che una combinazione
CP746, Space Technology and Applications International Forum—STAIF 2005, edited by M. S. El-Genk
© 2005 American Institute of Physics 0-7354-0230-2/05/$22.50
7
di proprietà del quadrispazio possa contribuire a cambiare l’indice di rifrazione n(τ, x, y, z), e queste proprietà
dovrebbero coinvolgere particelle che appartengono ai quattro universi paralleli.
CONCLUSIONE
Le proprietà del gravitone in spaziotempi con una costante cosmologica e alcune varianti della Relatività Speciale
suggeriscono nettamente che il nostro spaziotempo 3+1 sia un caso particolare in un quadrispazio più fondamentale.
Il quadrispazio può ospitare quattro spaziotempi elettromagneticamente ortogonali, uno dei quali è il nostro
spaziotempo, nel quale noi possiamo fisicamente operare solo in un singolo frame lungo τ, che è il “presente”. I
fenomeni gravitazionali possono permettere la navigazione nel quadrispazio, e non appena la tecnologia lo
permetterà, sarà possibile scoprire la possibile reale esistenza e la natura dei rimanenti tre spaziotempi. I fenomeni
gravitazionali osservati hanno gia mostrato che la massa totale dell’universo è quattro/cinque volte la massa
dell’universo visibile. Questa osservazione è incoraggiante per l’approccio presentato. In aggiunta, richiamando
l’introduzione, alcuni universi paralleli potrebbero essere universi di antimateria, perciò potrebbero diventare
preziose sorgenti di combustibile per astronavi equipaggiate di dispositivi o motori in grado di produrre campi
gravitazionali abbastanza intensi da catturare anche un limitato flusso di atomi da un universo parallelo.
Nel quadrispazio euclideo, esteso con la soluzione di Schwarzschild, che suggerisce l’esistenza di un indice di
rifrazione, le particelle possono viaggiare a velocità superiori a quella della luce senza produrre paradossi.
In base al modello più semplice, la proprietà più sconcertante del quadrispazio è che il “flusso del tempo” così come
percepito, è ovviamente un processo di “lettura/modifica” di una storia predeterminata o preregistrata, codificata
nell’indice di rifrazione. La visione dell’universo qui presentata “pressoché statica ma reattiva” differisce dalla
prima interpretazione della cosmologia in GR che era statica e senza eventi o possibilità di scelta. Abbandonando il
“tempo t” come principale dimensione in favore di quattro dimensioni spazio siamo portati a interpretare la realtà
come un “viaggio” in una sequenza preregistrata di possibilità nella quale gli oggetti materiali seguono le leggi della
fisica e gli essere senzienti possono agire scegliendo il loro percorso. E’ implicito che la sequenza preregistrata può
essere modificata tutte le volte che si effettua una “lettura”. Di conseguenza, ed in generale, ciò può accadere nel
“presente”, ma può anche accadere nel “futuro” e nel “passato” lungo la coordinata spazio τ rispetto al nostro
spaziotempo.
Come in Relatività Generale, il modello euclideo della realtà qui presentato è compatibile con un concetto simile ai
viaggi nel tempo. Non si tratta invero di viaggi nel tempo, bensì di viaggi-τ. Il tempo t locale (personale) non può
essere modificato perché dipende dall’invarianza di Lorentz, un viaggiatore τ può saltare dentro linee temporali
differenti (sequenze di τ frames) e ne può seguire attivamente lo svolgimento non appena la macchina per i viaggi-τ
si ferma. Nel quadrispazio questi sono comunque viaggi spaziali.
RINGRAZIAMENTI
L’autore desidera ringraziare Robert M. L. Baker jr. per utili discussioni.
BIBLIOGRAFIA
Almeida, J.B., “An alternative to Minkowski space-time,” v2, http://arxiv.org/abs/gr-qc/0407022 (2001), accessed July 16, 2004.
Almeida, J.B., “An Hypersphere model of the Universe – The dismissal of dark matter,” v3, http://arxiv.org/abs/Physics/0402075
(2004a), accessed July 16, 2004.
Almeida, J.B., “Euclidean formulation of general relativity,” v1, http://arxiv.org/abs/Physics/0406026 (2004b), accessed July 16,
2004.
Baker, R. M. L. Jr., “Precursor Proof-of-Concept Experiments for Various Categories of High-Frequency Gravitational Wave
(HFGW) Generators,” in Proceedings of Space Technology and Applications International Forum (STAIF-2004), edited by
M. S. El-Genk, AIP Conference Proceedings 699, Melville, NY, 2004, pp. 1093-1097.
Bostrom, N.,”Are you living in a computer simulation?” Philosophical Quarterly, 53, No. 211, pp. 243-255, (2003)
CP746, Space Technology and Applications International Forum—STAIF 2005, edited by M. S. El-Genk
© 2005 American Institute of Physics 0-7354-0230-2/05/$22.50
8
Deffayet, C., Dvali G., Gabadaze G., “Accelerated universe from gravity leaking to extra dimensions,” Physical Review D, 65,
044023-1 – 044023-9 (2002)
Dine, M., Kusenko A., “Origin of the matter-antimatter asymmetry,” Reviews of Modern Physics, 76, 1 – 30 (2004)
D’Inverno, R., Introducing Einstein’s Relativity, Clarendon Press, Oxford, (1996).
Fontana, G., “Gravitational Radiation and its Application to Space Travel,” in Proceedings of Space Technology and
Applications International Forum (STAIF-2000), edited by M. S. El-Genk, AIP Conference Proceedings 504, Melville, NY,
2000, pp. 1085-1092.
Fontana, G., “Gravitational Radiation Applied to Space Travel,” in Proceedings of the Gravitational-Wave Conference, edited by
P. Murad and R. Baker, The MITRE Corporation, Mclean, Virginia, May 6-9, Paper HFGW-03-111, 2003a.
Fontana, G. and Baker, R. M. L. Jr., “The High-Temperature Superconductor (HTSC) Gravitational Laser (GASER),” in
Proceedings of the Gravitational-Wave Conference, edited by P. Murad and R. Baker, The MITRE Corporation, Mclean,
Virginia, May 6-9, Paper HFGW-03-107, 2003b.
Fontana, G., “Design of a Quantum Source of High-Frequency Gravitational Waves (HFGW) and Test Methodology,” in
Proceedings of Space Technology and Applications International Forum (STAIF-2004), edited by M. S. El-Genk, AIP
Conference Proceedings 699, Melville, NY, 2004, pp. 1114-1121.
Germani, C., Sopuerta C. F., “String Inspired Brane World Cosmology,” Physical Review Letters, 88, 231101-1..4 (2002)
Gersten, A., “Euclidean Special Relativity,” Foundation of Physics, 33, 1237-1251 (2003)
Misner, C. W., Thorne, K. S. and Wheeler, J. A., Gravitation, Freeman, New York, 1973.
Montanus, J.M.C., “Proper-Time Formulation of Relativistic Dynamics,” Foundation of Physics, 31, 1357-1399 (2001)
Modanese, G., Fontana, G., “Effect of the Vacuum Energy Density on Graviton Propagation,” in Proceedings of Space
Technology and Applications International Forum (STAIF-2004) , edited by M. S. El-Genk, AIP Conference Proceedings
699, Melville, NY, 2004, pp. 1198-1205.
Peebles, P. J. E., Ratra B., “The cosmological constant and dark energy,” Reviews of Modern Physics, 75, 559 – 606 (2003)
Giorgio illustra il Modello a 4 Spaziotempi della Realtà alla Conferenza STAIF 2005. Titolo originale “The Four Spacetimes
Model of Reality”.
CP746, Space Technology and Applications International Forum—STAIF 2005, edited by M. S. El-Genk
© 2005 American Institute of Physics 0-7354-0230-2/05/$22.50
9
- Gravitational Wave Propulsion
Giorgio Fontana, University of Trento, Povo, Italy
[F04.] Near Term Propulsion Concepts-the Air-Breathing Mission
Chairs: Robert H. Frisbee, Jet Propulsion Laboratory, Pasadena, CA, USA
David Goodwin, US Department of Energy, Washington, DC, USA
- Combining MHD Airbreathing and Fusion Rocket Propulsion for Earth-to-Orbit for Earth-to-Orbit Flight
H.D. Froning, Jr., Flight Unlimited, Flagstaff, AZ; G.H. Miley, Nie Luo, Yang Yang, E. Burton, University of Illinois, Urbana, IL; H. Momota,
NPL Associates, Champaign,
- Concept for Space Technology Advancement
Jeremiah J. Hansen, Fredrecksburg, VA
- Regenerative Aerobraking
Robert W. Moses, NASA Langley Research Center, Hampton, VA
- Tweaking Flux Capacitors
J.F. Woodward, California State University, Fullerton, CA
[F05.] Far Term Propulsion Concepts - the Deep Space Mission
Chairs: Glen A. (Tony) Robertson, NASA Marshall Space Flight Center, Marshall Space Flight Center, AL, USA
H. David Froning, Jr., Flight Unlimited, Flagstaff, AZ, USA
- Manipulating the Vacuum Scalar Field with Superconductors: A Search for Exotic Material
Glen A. Robertson, Gravi Atomi Research, Madison, AL
- Overview of Theories and Experiments of Electromagnetic Inertia Manipulation Propulsion
H.H. Brito, Instituto Universitario Aeronautico, Cordoba, Argentina; S.A. Elaskar, Universidad Nacional de Cordoba
- Quantum Vacuum Pathway Theory
Eric Habegger, Davis Systems, Lakeport, CA
- Extracting Energy from Cosmic Electromagnetic Fields and Plasmas by a Chaotic Gun Effect for Relativistic
Charged Particles
Ciprian Ciubotariu, Universite Laval, Quebec, Canada; Carmen-Iuliana Ciubotariu, University of Calgary, Canada; Corneliu Ciubotariu,
Technical University of Iasi, Romania
[F07.] Theoretical Considerations, Warp Drives Faster than Light Speed Travel and Other Concepts - I
Chairs: Frank Mead, Air Force Research Laboratory, Edwards AFB, CA, USA
Paul Murad, U.S. Department of Defense, Vienna, VA, USA
- Heim Quantum Theory for Space Propulsion Physics
Walter Droscher, Jochem Hauser, Institut fur grenzgebiete der Wissenschaft, Austria
- Warp Drives: The Dreams and the Realities - Part II: Potential Solutions
P.A. Murad, Department of Defense
- A Perspective of Practical Interstellar Exploration: Using Field Propulsion and Hyper-Space Navigation
Y. Minami, NEC Patent Service, Ltd., Tokyo, Japan
- The Four Spacetimes Model of Reality
Girogio Fontana, University of Trento, Povo, Italy
17