momento

Prof. Fernando D’Angelo. classe 5BS . a.s. 2012/2013
Il momento torcente su una spira percorsa da corrente posta in campo magnetico.
Il momento torcente è innanzitutto un vettore.
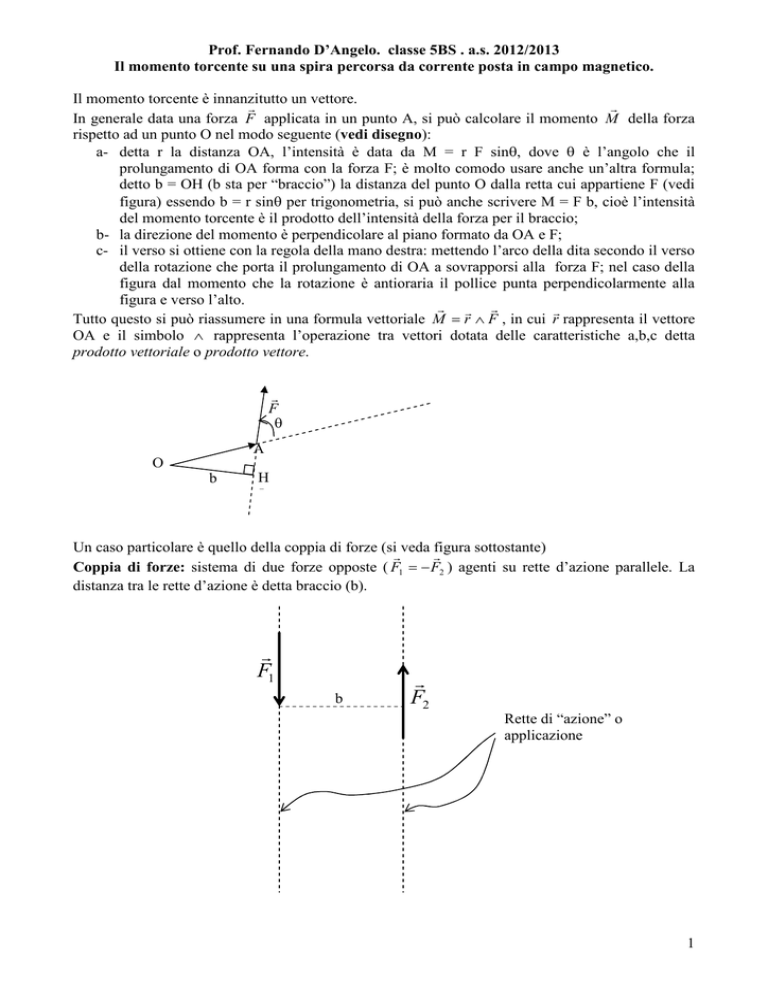
In generale data una forza F applicata in un punto A, si può calcolare il momento M della forza
rispetto ad un punto O nel modo seguente (vedi disegno):
a- detta r la distanza OA, l’intensità è data da M = r F sinθ, dove θ è l’angolo che il
prolungamento di OA forma con la forza F; è molto comodo usare anche un’altra formula;
detto b = OH (b sta per “braccio”) la distanza del punto O dalla retta cui appartiene F (vedi
figura) essendo b = r sinθ per trigonometria, si può anche scrivere M = F b, cioè l’intensità
del momento torcente è il prodotto dell’intensità della forza per il braccio;
b- la direzione del momento è perpendicolare al piano formato da OA e F;
c- il verso si ottiene con la regola della mano destra: mettendo l’arco della dita secondo il verso
della rotazione che porta il prolungamento di OA a sovrapporsi alla forza F; nel caso della
figura dal momento che la rotazione è antioraria il pollice punta perpendicolarmente alla
figura e verso l’alto.
Tutto questo si può riassumere in una formula vettoriale M = r ∧ F , in cui r rappresenta il vettore
OA e il simbolo ∧ rappresenta l’operazione tra vettori dotata delle caratteristiche a,b,c detta
prodotto vettoriale o prodotto vettore.
F
θ
A
O
b
H
J
Un caso particolare è quello della coppia di forze (si veda figura sottostante)
Coppia di forze: sistema di due forze opposte ( F1 = − F2 ) agenti su rette d’azione parallele. La
distanza tra le rette d’azione è detta braccio (b).
F1
b
F2
Rette di “azione” o
applicazione
1
Calcolo del momento di una coppia di forze.
Quando si calcola il momento di una coppia di forze si sceglie per comodità come punto di
riferimento uno dei punti di applicazione delle forze. Ad esempio in relazione alla figura sottostante
il punto A. Calcolando separatamente il momento delle due forze rispetto al punto A si vede che:
a- il momento della forza F1 rispetto al punto A è zero perché è zero il braccio della forza F1
(il punto A appartiene alla retta di azione della forza F1 !!);
b- il momento della forza F2 ha intensità data da : M 2 = F b , essendo F il valore comune
dell’intensità delle due forze.
F2
A
b
O
B
F1
L’intensità del momento totale di una coppia di forze è dunque data da M = F b
Per quanto riguarda direzione e verso, la direzione è perpendicolare al piano della coppia di forze, il
verso si ottiene con la regola della mano destra.
Il momento di una coppia di forze viene detto comunemente momento torcente (in inglese
“torque”) perché il suo effetto è quello di mettere in rotazione il corpo a cui la coppia di forze
è applicata.
Osservazione. Se si fossero calcolati i momenti delle due forze rispetto al punto medio O i calcoli
sarebbero stati:
M1 = F b / 2
M2 = F b/2
ma essendo i due momenti concordi, l’intensità del momento totale sarebbe ancora data da
M = M1 + M 2 = F b / 2 + F b / 2 = F b .
Da qui la comodità di scegliere come punto di riferimento uno dei punti applicazione delle forze.
2
Passiamo adesso alla spira rettangolare percorsa da corrente immersa in un campo magnetico
uniforme (vedi pag 692 del libro di testo).
Su due lati della spira, quando il piano della spira è parallelo al campo magnetico, agiscono due
forze di uguale intensità F = I L B (coppia di forze), essendo L la lunghezza dei lati. Il braccio della
coppia di forze è w; quindi il momento torcente indicato con τ ha intensità pari a
τ = Fw = I B Lw = I A B
essendo A= L w l’area della spira.
Quando la spira inizia a ruotare, si vedano le figure del testo, le forze hanno la stessa intensità ma il
valore del braccio dipende dall’angolo e allora il momento torcente è dato da:
τ = I A B sin θ
Questa formula si può scrivere elegantemente
usando una notazione vettoriale. Vediamo come.
Definiamo momento magnetico µ della spira il
vettore che ha direzione perpendicolare al piano
della spira, il verso dato dalla regola della mano
destra e l’intensità data dalla formula µ = I A ,
essendo I la corrente e A l’area della spira. Il
vettore momento magnetico si può pensare
applicato al centro della spira (vedi figura a lato).
I
Allora il momento torcente si può scrivere
vettorialmente nel modo seguente:
τ = µ ∧B
dove ∧ rappresenta l’operazione di prodotto
vettoriale tra i vettori momento magnetico e campo magnetico.
Quando si calcola l’intensità si usa la formula τ = µ B sin θ = I A B sin θ , dove θ è l’angolo formato
µ
dai vettori µ e B , cioè dalla normale al piano della spira e dal campo magnetico.
3