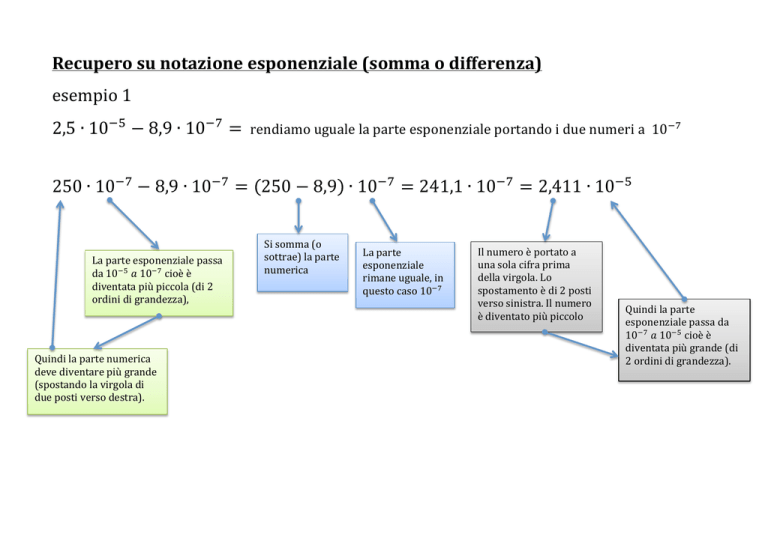
Recupero su notazione esponenziale (somma o differenza) esempio 1 2,5 ∙ 10!! − 8,9 ∙ 10!! = rendiamo uguale la parte esponenziale portando i due numeri a 10!! 250 ∙ 10!! − 8,9 ∙ 10!! = 250 − 8,9 ∙ 10!! = 241,1 ∙ 10!! = 2,411 ∙ 10!! La parte esponenziale passa da 10!! 𝑎 10!! cioè è diventata più piccola (di 2 ordini di grandezza), Quindi la parte numerica deve diventare più grande (spostando la virgola di due posti verso destra). Si somma (o sottrae) la parte numerica La parte esponenziale rimane uguale, in questo caso 10!! Il numero è portato a una sola cifra prima della virgola. Lo spostamento è di 2 posti verso sinistra. Il numero è diventato più piccolo Quindi la parte esponenziale passa da 10!! 𝑎 10!! cioè è diventata più grande (di 2 ordini di grandezza). Recupero su notazione esponenziale (somma o differenza) esempio 2 2,5 ∙ 10!! + 8,9 ∙ 10!! = rendiamo uguale la parte esponenziale portando i due numeri a 10!! 2,5 ∙ 10!! + 0,089 ∙ 10!! = 2,5 + 0,089 ∙ 10!! = 2,589 ∙ 10!! Quindi la parte numerica deve diventare più piccola (spostando la virgola di due posti verso sinistra). La parte esponenziale passa da 10!! 𝑎 10!! cioè è diventata più grande (di 2 ordini di grandezza), Si somma (o sottrae) la parte numerica La parte esponenziale rimane uguale, in questo caso 10!! Recupero su notazione esponenziale (moltiplicazione) esempio 3 2,5 ∙ 10!! ∙ 8,9 ∙ 10! = è sufficiente moltiplicare tra loro la parte numerica e la parte esponenziale 2,5 ∙ 8,9 ∙ 10!! ∙ 10! = 22,25 ∙ 10(!!!!) = 22,25 ∙ 10! = 2,225 ∙ 10! Moltiplicazione tra le parti numeriche Moltiplicazione tra le parti esponenziali Prodotto della parte numerica Gli esponenti vengono sommati algebricamente Il numero è portato a una sola cifra prima della virgola. Lo spostamento è di un posto verso sinistra. Il numero è diventato più piccolo Quindi la parte esponenziale passa da 10! 𝑎 10! cioè è diventata più grande (di un ordine di grandezza). Recupero su notazione esponenziale (divisione) esempio 4 !,!∙!"!!
!,!∙!"!
= è sufficiente dividere tra loro la parte numerica e la parte esponenziale !,! !"!!
!,!
∙
!"!
Valore della divisione tra le parti numeriche divisione tra le parti esponenziali Divisione tra le parti numeriche = 0,281 ∙ 10!! ∙ 10!! = 0,281 ∙ 10
Portiamo al numeratore la parte esponenziale che era al denominatore, cambiando il segno dell’esponente. In questo caso da 10! 𝑎 10!! !!!!
= 0,281 ∙ 10!!" = 2,81 ∙ 10!!" Gli esponenti vengono sommati algebricamente Il numero è portato a una sola cifra (diversa da zero) prima della virgola. Lo spostamento è di un posto verso destra. Il numero è diventato più grande Quindi la parte esponenziale passa da 10!!" 𝑎 10!!" cioè è diventata più piccola (di un ordine di grandezza). Esercizi (da svolgere facendo tutti i passaggi come visto negli esempi) 1,25 ∙ 10! ∙ 2,91 ∙ 10! = 𝑟𝑖𝑠𝑢𝑙𝑡𝑎𝑡𝑜 3,64 ∙ 10!" 8,25 ∙ 10!!" ∙ 9,91 ∙ 10! = 𝑟𝑖𝑠𝑢𝑙𝑡𝑎𝑡𝑜 8,18 ∙ 10!!! 6,21 ∙ 10! ∙ 6,11 ∙ 10!! = 𝑟𝑖𝑠𝑢𝑙𝑡𝑎𝑡𝑜 3,79 ∙ 10!! 6,5 ∙ 10!"
!!
=
𝑟𝑖𝑠𝑢𝑙𝑡𝑎𝑡𝑜 1,33
∙
10
4,9 ∙ 10!!
3,5 ∙ 10!!
= 𝑟𝑖𝑠𝑢𝑙𝑡𝑎𝑡𝑜 3,93 ∙ 10!!" !
8,9 ∙ 10
1,3 ∙ 10!"
!
=
𝑟𝑖𝑠𝑢𝑙𝑡𝑎𝑡𝑜 1,65
∙
10
7,9 ∙ 10!
1,25 ∙ 10! − 2,91 ∙ 10! = 𝑟𝑖𝑠𝑢𝑙𝑡𝑎𝑡𝑜 − 2,90 ∙ 10! 8,25 ∙ 10!!" + 9,91 ∙ 10!!" = 𝑟𝑖𝑠𝑢𝑙𝑡𝑎𝑡𝑜 9,99 ∙ 10!!" 6,21 ∙ 10!! + 6,11 ∙ 10! = 𝑟𝑖𝑠𝑢𝑙𝑡𝑎𝑡𝑜 6,27 ∙ 10!!









