Un triangolo equilatero con lato uguale a BC - 4Bclasse2-0

Quesiti di matematica
1.
Nella disequazione (𝑎 + 𝑏)2 − (𝑎 − 𝑏)2 > 0 , i termini a e b NON devono essere:
-
Concordi
Maggiori di 0
Minori di 0
Discordi
Risoluzione: 4ab > 0
4: discordi, perché se sarebbero concordi 4 si moltiplicherebbe SEMPRE per un
numero positivo e sarebbe maggiore di 0; mentre se fossero discordi 4 si
moltiplicherebbe per un numero NEGATIVO, minore di 0
2.
Nella figura OA è uguale a 27 unità e OB a 36. Ricavare la lunghezza di AB.
B
O
-
55 unità
63 unità
45 unità
60 unità
A
Risoluzione:
45 unità: infatti, applicando il teorema di Pitagora si scopre che il raggio della
circonferenza è di 45 unità, e le due diagonali del rettangolo sono uguali.
3.
Il numero 6637₈ è uguale a … in base 10
-
3766
3487
5773
3852
Risoluzione:
3487: infatti 7 × 1 = 7; 3 × 8 = 24; 6 × 82 = 384; 6 × 83 = 3072, che sommati
fanno 3487
4.
Nel parallelogramma in figura BD è perpendicolare ai due lati paralleli AB e CD, e gli
angoli BÂD e DĈB sono uguali a 60°. Il suo perimetro è uguale a quello di:
-
Un triangolo equilatero con lato uguale a BC
Un quadrato con lato uguale a BC
Un rettangolo con lati uguali ad AB e BC
Un triangolo equilatero con lato BD
D
A
B
C
Risoluzione:
- Un triangolo equilatero con lato uguale a BC
Infatti se si capovolgesse verticalmente il triangolo rettangolo BCD si otterrebbe un
triangolo equilatero (infatti gli angoli ADB e DBC sono di 30°, perché 180° (somma
angoli interni triangolo) – 60° (BÂD e DĈB) = 30°, e due angoli di 30° sommati
formano un angolo di 60°, uguale agli altri due), e il perimetro sarebbe uguale a
quello del triangolo equilatero di lato AD.
5.
Nell’equazione di secondo grado parametrica 𝑥 2 − 𝑘𝑥 + 1 = 0, il parametro k
sarebbe uguale a … se la somma delle radici fosse uguale a 2 (senza considerare la
condizione di realtà)
-
-2
1
-1
2
𝑏
Risoluzione: 2, infatti la somma delle radici 𝑥1 + 𝑥2 è uguale a - , ovvero k =2
𝑎
6.
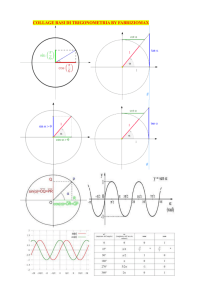
Nel SI gli angoli si misurano in radianti, non in gradi sessagesimali.
Un arco di circonferenza con lunghezza uguale al raggio della stessa descrive un
angolo di un radiante. Un angolo retto è uguale a ... radianti.
-
𝜋
𝜋/2
𝜋/4
2𝜋
Risoluzione: 𝝅/2, infatti la misura della circonferenza è uguale a 2𝜋r, quindi a 2𝜋
radianti. Un angolo retto è uguale a ¼ di circonferenza, quindi
2𝜋
4
=
𝜋
2
7.
In un sacchetto sono contenute 50 biglie, tra cui 20 bianche, 15 rosse e 15 verdi.
Se si togliessero 13 biglie rosse, quale sarebbe la probabilità di estrarre una biglia
rossa ?
-
1 su 20
1 su 13
1 su 15
1 su 17,5
Risoluzione: 1 su 17,5, infatti se si tolgono 13 biglie, 37 ne restano nel sacchetto, tra
cui ci sono anche le due biglie rosse, e 2/37 = 1/17,5
8.
Un quadrato e un rettangolo sono isoperimetrici (hanno lo stesso perimetro).
Possono avere anche la stessa area?
-
Si
No
Si, solo in un caso
Si, solo in 2 casi.
Risoluzione:
NO, ad esempio un quadrato con lato 4 ha perimetro uguale a 16 e area uguale a 16.
Un rettangolo con area 16 può avere lati uguali a 2 e 8 o 1 e 16, ma non avrà mai il
perimetro uguale a 16 (nel primo è uguale a 20, nel secondo a 34)
9. Nella disequazione fratta
-
𝑥
𝑥
𝑥
𝑥
< −5 ∨ 𝑥 > 6
< −6 ∨ 𝑥 > 5
< −5 ∨ 𝑥 > −6
<5∨𝑥 >6
58𝑥−2(𝑥+29𝑥−5)
𝑥−6
>0…
Risoluzione:
𝒙 < −𝟓 ∨ 𝒙 > 𝟔 è la soluzione che si ottiene studiando il segno della disequazione
in forma normale
−2𝑥−10
>
𝑥−6
0
10.
Nel piano cartesiano i punti A (4;1), B (7;2) e C (5;4) formano un triangolo.
Il triangolo 1 è descritto dai punti A1 (1;5), B1 (4;6) e C1 (2;8) e il triangolo 2 dai
punti A2 (9;4), B2 (10;7) e C2 (7;6).
-
TR1 rappresenta una traslazione e TR2 una simmetria assiale
TR1 rappresenta una traslazione e TR2 una rotazione
TR1 rappresenta una rotazione e TR2 una simmetria assiale
TR1 e TR2 rappresentano due rotazioni
Risoluzione:
TR1 rappresenta una traslazione e TR2 una simmetria assiale, che si vedono
chiaramente costruendo le due figure.
TR1
TR2
TR
r