Esercizi e Complementi cap 1

TEORIA DELLA STIMA E DELLA DESCISIONE STATISTICA
STIMA A MASSIMA VEROSIMIGLIANZA
Per determinare la stima a massima verosimiglianza di un parametro θ, partendo da un campione di dati X,
bisogna scrivere la densità di probabilità f(x;θ) dipendente dal parametro incognito θ . Successivamente si
ricava la funzione di verosimiglianza oppure il suo logaritmo:
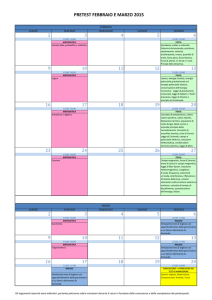
N
L(θ ) = ∏ f ( xi ;θ )
i =1
N
ln[ L(θ )] = ∑ ln[ f ( xi ;θ )]
i =1
Per procedere nella stima a massima verosimiglianza, basta semplicemente verificare che ln[L(θ)] sia
derivabile, calcolare la derivata prima e ricavare il valore di θ per cui si annulla:
∂ ln[ L(θ )]
=0
∂θ
θ =θˆML
Le stime a massima verosimiglianza vengono in genere indicate con Θ̂ ML . Le principali proprietà di cui
godono sono:
‰ Le stime Θ̂ ML sono consistenti;
‰ Le stime Θ̂ ML sono asintoticamente efficienti;
‰ Se per il problema in esame esiste uno stimatore efficiente, esso è proprio lo stimatore Θ̂ ML
Inoltre se ϕ(θ) è una funzione invertibile del parametro θ, la stima a massima verosimiglianza di ϕ(θ), sarà
proprio ϕ (θˆML ) .
2
Esercizi e Complementi
Esercizio 1.1
Determinare la stima a massima verosimiglianza del valor medio e della varianza di un campione di dati
X =(x1, x2, …, xN) gaussiano N(μ,σ2)
Il primo passo è di scrivere la funzione di verosimiglianza:
N
N
L( μ ,σ ) = ∏ f ( xi ;θ ) =∏
1
2
i =1
i =1
2πσ 2
−
e
( xi − μ )2
2σ 2
passando al logaritmo:
ln[ L( μ , σ 2 )] = −
1
N
N
ln(2π ) − ln(σ 2 ) −
2
2
2σ 2
N
∑ (x
i =1
i
− μ)2
le derivate parziali valgono:
∂ ln[ L( μ ,σ 2 )] 1 N
= 2 ∑ ( xi − μ )
∂μ
σ i =1
∂ ln[ L( μ ,σ 2 )]
N
1 N
=
−
+
∑ ( xi − μ ) 2
∂σ 2
2σ 2 2σ 4 i =1
I valori per cui si annullano sono le stime a massima verosimiglianza dei parametri, rispettivamente:
μ̂ ML =
1 N
∑ xi
N i =1
2
σˆ ML
=
1 N
( xi − μˆ ML ) 2
∑
N i =1
che corrispondono alla media e alla varianza campionaria.
Modelli e Metodi per la Simulazione
3
Complemento 1.1
Per verificare la bontà della stima ottenuta bisogna verificare che le stime siano corrette. Per il valor
medio si ha:
E[ μˆ ML ] =
1
N
N
∑ E[ x ] = μ
i
i =1
Poiché il valor medio dello stimatore coincide con il parametro da stimare, la stima si definisce non
polarizzata. Per verificare se la stima del valor medio μ̂ ML è una stima efficiente bisogna confrontare la
varianza della stima con il limite di Cramer-Rao, a tal proposito è necessario ricordare la disuguaglianza di
Cramer-Rao che nel caso specifico vale:
Var[ μˆ ML ] ≥
1
⎡⎛ ∂ ln[ f ( x; μ , σ 2 )] ⎞ 2 ⎤
⎟ ⎥
E ⎢⎜⎜
⎟ ⎥
∂μ
⎢⎝
⎠ ⎦
⎣
=
σ2
N
Per calcolare la varianza della stima μ̂ ML bisogna eseguire la seguente operazione:
⎡1
Var[ μˆ ML ] = Var ⎢
⎣N
N
∑
i =1
⎤ σ2
xi ⎥ =
⎦ N
Poiché la varianza della stima coincide con il limite di Cramer-Rao, possiamo concludere che la media
campionaria μ̂ ML ottenuta dalla stima a massima verosimiglianza del valor medio di un campione dati
gaussiano è una stima efficiente. Inoltre per quanto visto prima è anche una stima non polarizzata e
consistente, in definitiva è la migliore stima possibile che possiamo ottenere per questo tipo di parametro.
Questo risultato è valido sia se la varianza del campione è nota, e sia se è incognita come in questo caso.
Complemento 1.2
Le stesse verifiche effettuate per la stima del valor medio possono essere effettuate per la stima della
2
. Il risultato della stima a massima verosimiglianza suggerisce di utilizzare la
varianza del campione σˆ ML
varianza campionaria come stima della varianza di un campione gaussiano. Purtroppo la varianza
campionaria non è una stima corretta infatti:
4
Esercizi e Complementi
[ ]
2
E σˆ ML
=
1
N
∑ E [( x
N
i
]
− μˆ ML ) 2 =
i =1
N −1 2
σ
N
In questo caso la stima si dice polarizzata, e la sua polarizzazione b vale:
[ ]
2
b = E σˆ ML
−σ 2 = −
σ2
N
uno stima non polarizzata è ad esempio:
2
σˆ NP
=
N
2
σˆ ML
N −1
Il limite di Cramer-Rao, richiede un calcolo più laborioso:
2
Var[σˆ ML
]≥
2
⎛
∂b(σˆ ML
)⎞
⎟
⎜1 +
2
⎟
⎜
∂σ
⎠
⎝
⎡⎛ ∂ ln[ f ( x; μ , σ 2 )] ⎞ 2 ⎤
⎟ ⎥
E ⎢⎜⎜
⎟ ⎥
⎢⎝
∂σ 2
⎠ ⎦
⎣
=
2σ 4
N
1⎞
⎛
⎜1 − ⎟
N
⎝
⎠
2
2
Per calcolare la varianza di σˆ ML
. Consideriamo la seguente variabile:
χ2 =
N −1
σ2
2
σˆ NP
Si dimostra che questa variabile ha una densità di probabilità del Chi-quadro con N – 1 gradi di libertà, e
la sua varianza vale:
[ ]
Var χ 2 = 2( N − 1)
pertanto:
Modelli e Metodi per la Simulazione
[ ]
Var σ
2
ˆ ML
2
[ ]
⎡ N −1 2 ⎤ ⎛ N −1⎞
⎛ N −1⎞
2
= Var ⎢
σˆ NP ⎥ = ⎜
⎟ Var σˆ NP = ⎜
⎟
⎣ N
⎦ ⎝ N ⎠
⎝ N ⎠
2
2
5
[ ]
⎛ σ2 ⎞
2
⎜
⎟
⎜ N − 1 ⎟ Var χ
⎝
⎠
In definitiva:
[ ]
⎛ N −1⎞
2
Var σˆ ML
=⎜
⎟
⎝ N ⎠
2
2
2
⎛ σ2 ⎞
N − 1 ⎞ 2σ 4 2σ 4
⎟ 2( N − 1) = ⎛⎜
⎜
=
⎟
⎜ N −1⎟
N
⎝ N ⎠ N −1
⎝
⎠
1⎞
⎛
⎜1 − ⎟
N⎠
⎝
Confrontando questa espressione con il limite di Cramer-Rao, appare evidente che la varianza
campionaria ha una varianza di stima sempre superiore al limite di Cramer-Rao, quindi la stima a massima
verosimiglianza della varianza di un campione dati non è una stima efficiente, ma tende al limite di
Cramer-Rao solo per N → ∞. In questo caso la stima si dice asintoticamente efficiente. Possiamo
riepilogare quanto detto dicendo che la stima a massima verosimiglianza di un campione dati gaussiano è
2
la varianza campionaria di σˆ ML
, la quale risulta essere una stima consistente(in quanto stima ML), una
stima non corretta (perché polarizzata), ed una stima asintoticamente efficiente. A questo punto è
interessante confrontare le proprietà della varianza campionaria con quelle della stima non polarizzata
2
determinata in precedenza σˆ NP
:
[ ]
2
=
Var σˆ NP
2σ 4
N −1
2
Poiché la varianza di questa stima è maggiore della varianza della stima σˆ ML
, dobbiamo concludere che la
stima a massima verosimiglianza della varianza di un campione di dati gaussiano, sebbene sia una stima
polarizzata, ha una bontà maggiore di qualsiasi altra stima, poiché è quella a varianza minore.
6
Esercizi e Complementi
Esercizio 1.2
Determinare la stima a massima verosimiglianza del valor medio di una v.a. esponenziale negativa
utilizzando il campione di dati X =(x1, x2, …, xN)
Il primo passo è di scrivere la funzione di verosimiglianza:
L( μ ) =
N
∏
f ( xi ; μ ) =
i =1
1
μ
N
−
e
1
μ
( x1 + x2 +L+ x N )
passando al logaritmo:
ln[ L( μ )] = − N ln(μ ) −
1
μ
(x1 + x 2 + L + x N )
la derivata vale:
∂ ln[ L( μ )]
1
N
= − + 2 (x1 + x 2 + L + x N )
∂μ
μ μ
Il valore per cui si annulla è la stima a massima verosimiglianza del parametro:
μ̂ ML =
(x1 + x 2 + L + x N )
N
che corrispondono alla media campionaria. Anche la media campionaria è una stima non polarizzata,
consistente ed efficiente, quindi la miglior stima per il valor medio di una v.a. esponenziale negativa
Modelli e Metodi per la Simulazione
7
Esercizio 1.3
Sia λ il numero medio di chiamate ricevute in un’ora in una centrale telefonica. Ipotizzando che il numero
effettivo di chiamate orarie sia modellabile con una variabile aleatoria discreta di Poisson, con valor
medio pari a λ, e di avere a disposizione N osservazioni indipendenti del fenomeno, determinare:
‰ La stima a massima verosimiglianza del parametroλ.
‰ La polarizzazione della stima ottenuta;
‰ Verificare la consistenza e l’efficienza della stima ottenuta
Ricordiamo che una v.a. discreta di Poisson a funzione massa di probabilità pari a :
pn =
λn
n!
e −λ
inoltre:
E[ n] = Var[n] = λ
Il primo passo è di scrivere la funzione di verosimiglianza, sostituendo opportunamente la funzione
densità di probabilità con la funzione massa di probabilità, perché questa volta il problema riguarda una
v.a. discreta, ed il campione delle osservazioni è (n1,n2…,nN):
L (λ ) =
N
λni
N
∏ p λ =∏ n ! e
i,
i =1
i =1
λ∑i =1
N
−λ
i
=
ni
N
∏n !
e − Nλ
i
i =1
passando al logaritmo:
ln[ L( μ )] = ln(λ )
N
∑
i =1
la derivata vale:
ni −
N
∑ ln(n !) − Nλ
i
i =1
8
Esercizi e Complementi
∂ ln[ L(λ )] 1
=
∂λ
λ
N
∑n
i
−N
i =1
Il valore per cui si annulla è la stima a massima verosimiglianza del parametro:
λ̂ ML =
1
N
N
∑n
i
i =1
Per verificare se la stima è corretta (non polarizzata):
[ ]
1
E λˆML =
N
N
∑ E[ n ] = λ
i
i =1
La stima ottenuta mediante la tecnica a massima verosimiglianza è la media campionaria, e risulta essere
una stima corretta. Poiché si tratta di una stima ML è anche consistente. Per verificare se la stima è
efficiente bisogna calcolare la varianza della stima e confrontarla con il limite di Cramer-Rao. Poiché per
ipotesi le N osservazioni sono indipendenti, la varianza si può calcolare come il prodotto delle singole
varianze:
[ ]
Var λˆML =
1
N2
λ
N
∑ Var[n ] = N
i
i =1
Il limite di Cramer-Rao è:
Var[λˆML ] ≥
1
⎡⎛ ∂ ln p , ] ⎞
iλ
⎟⎟
E ⎢⎜⎜
λ
∂
⎢⎝
⎠
⎣
2
⎤
⎥
⎥
⎦
=
1
⎡ ∂ ⎛1
E ⎢ ⎜⎜
⎢⎣ ∂λ ⎝ λ
N
∑n
i =1
i
⎞⎤
− N ⎟⎟⎥
⎠⎥⎦
=
1
⎡1
E⎢ 2
⎣λ
⎤
N
∑ n ⎥⎦
i
i =1
=
1
⎛ 1
⎜
⎜ λ2
⎝
⎞
N
∑ E[n ]⎟⎟⎠
=
i
i =1
Poiché la varianza della stima coincide con il limite di Cramer-Rao la stima è efficiente.
λ
N
Modelli e Metodi per la Simulazione
9
Esercizio 1.4
Si consideri un esperimento che può avere solo due risultati: “successo” o “insuccesso” e che essere
ripetuto N volte. Ipotizzando che la probabilità dell’evento “successo” sia pari a p, e che durante le N
prove dell’ esperimento l’evento favorevole si è verificato k volte, determinare una stima non polarizzata
del parametro p e verificarne la consistenza.
La variabile aleatoria discreta che descrive l’esercizio è una v.a. binomiale la cui funzione massa di
probabilità vale:
⎛N⎞
p k = ⎜⎜ ⎟⎟ p k (1 − p ) ( N − k )
⎝k⎠
Chiaramente la funzione massa di probabilità è funzione del parametro p, inoltre è anche la funzione di
verosimiglianza, quindi per determinare la stima ML è sufficiente derivare pk.:
⎛ N ⎞ k −1
⎛N⎞
dL( p) dp k
d ⎡⎛ N ⎞ k
( N −k ) ⎤
( N −k )
=
=
− ⎜⎜ ⎟⎟( N − k ) p k (1 − p ) ( N − k −1)
⎢⎜⎜ ⎟⎟ p (1 − p )
⎥ = ⎜⎜ ⎟⎟kp (1 − p )
dp
dp dp ⎣⎝ k ⎠
⎝k⎠
⎦ ⎝k⎠
la derivata si annulla per
dL( p )
dp
= 0 ⇒ pˆ ML =
p = pˆ ML
k
N
poiché si tratta di una v.a. binomiale il valor medio e la varianza di k sono:
E[ k ] =
N
∑ kp
k
=Np
k =0
Var[k ] = E[k 2 ] − E 2 [k ] = Np(1 − p)
Verifichiamo se la stima ML è una stima polarizzata:
10
Esercizi e Complementi
E[ pˆ ML ] =
E[k ]
=p
N
La stima ML del parametro p è una stima corretta.
Var[ pˆ ML ] =
Var[k ] p(1 − p)
=
N
N2
Poiché:
lim Var[ pˆ ML ] = 0
N →∞
La stima ML del parametro p è una stima consistente.
Modelli e Metodi per la Simulazione
11
DISTRIBUZIONE NORMALE STANDARD
La distribuzione normale standard si indica con Φ(z), e la sua espressione vale:
z
1
Φ( z ) =
2π
∫e
−
x2
2
dx
−∞
La funzione Φ(z), rappresenta l’area sottesa ad una curva gaussiana di valor medio nullo, e varianza
unitaria. Questa espressione permette di calcolare la probabilità degli eventi X ≤ z, quando X è appunto,
una v.a. gaussiana a media nulla, e varianza unitaria.
Φ (z)
-3.5
0.4
z
3.5
x
Ogni v.a. gaussiana X ∈ N(μ,σ2), può essere normalizzata alla v.a. gaussiana standard Z mediante la
trasformazione:
Z=
X −μ
σ2
In appendice, nella tavola A.1, viene riportata la tabella con i valori di Φ(z). Anche se la curva è definita
nell’intervallo ]-∞,+∞[ , in pratica assume valori significati nell’intervallo [-3.5, +3.5]. Per questo motivo
nelle tabelle vengono riportati soltanto in questo intervallo. Inoltre poiché la curva gaussiana è una
funzione simmetrica, la funzione Φ(z), gode della seguente proprietà:
Φ (− z ) = 1 − Φ ( z )
Pertanto la tabella riporta soltanto i valori nell’intervallo [0, +3.5].
12
Esercizi e Complementi
Esercizio 1.5
Mediante l’utilizzo della tavola statistica Tav. A1 (che riporta i valori della distribuzione normale
standard), calcolare la probabilità che la v.a. gaussiana X ∈ N(4,4), assuma valori tra 3 e 5.
La prima operazione da effettuare è normalizzare la v.a. X alla gaussiana standard, e successivamente e
seguire il calcolo della probabilità. In pratica:
⎛5− 4⎞
⎛3− 4⎞
Pr{3 < X < 5} = Φ⎜
⎟ − Φ⎜
⎟ = Φ (0.5) − Φ (−0.5) = Φ (0.5) − [1 − Φ (0.5)]
⎝ 2 ⎠
⎝ 2 ⎠
Dalla tabella si ha: Φ(0.5) = 0.6915, si ha:
Pr{3 < X < 5} = 0.383
Esercizio 1.6
La quantità di carburante, in migliaia di litri, richiesta settimanalmente ad una stazione di servizio, può
essere schematizzata come una v.a. gaussiana X ∈ N(20,16). Sapendo che la stazione viene
completamente rifornita all’inizio di ogni settimana, si chiede di calcolare la capacità C del serbatoio, in
modo che la probabilità di esaurire il carburante nella settimana risulti 0.01
Poiché la probabilità che il carburante richiesto dalla stazione superi la capacità del deposito deve essere
0.01, si ha:
Pr{X > C } = 0.01
e poiché:
⎛ C − 20 ⎞
Pr{X > C} = 1 − Pr{X < C} = 1 − Φ⎜
⎟ = 0.01
⎝ 4 ⎠
da cui:
Modelli e Metodi per la Simulazione
13
⎛ C − 20 ⎞
Φ⎜
⎟ = 0.99
⎝ 4 ⎠
Dalla tabella si ha:
C − 20
≈ 2.33 ⇒ C ≈ 29,32
4
Quindi la capacità del serbatoio deve essere circa di 29,32 migliaia di litri.
Complemento 1.3
Le variabili aleatorie gaussiane godono di alcune importanti proprietà, tra le quali, ricordiamo che due v.a.
gaussiane incorrelate sono anche indipendenti. Un’altra proprietà riguarda la somma di due v.a. gaussiane
In particolare se una v.a. V è combinazione lineare di due v.a. gaussiane X e Y incorrelate
V = aX + bY
E’ una v.a. gaussiana con i seguenti parametri:
μ V = aμ X + bμ Y
σ V2 = aσ X2 + bσ Y2
Questo risultato può essere esteso anche alla combinazione lineare di N v.a. gaussiane.
Se invece le due v.a. non sono incorrelate, le relazioni date sopra non sono valide. Nel caso di due v.a.
gaussiane correlate con grado di correlazione pari a ρ può essere interessante calcolare le probabilità
condizionate X|Y e Y|X. In questo caso valgono le seguenti relazioni:
E [X Y = y ] = μ X + ρ
σX
( y − μY )
σY
(
Var [X Y = y ] = σ X2 1 − ρ 2
)
14
Esercizi e Complementi
E [Y X = x ] = μ Y + ρ
σY
(x − μ X )
σX
(
Var [Y X = x ] = σ Y2 1 − ρ 2
)
Esercizio 1.7
Un operaio A per compiere un lavoro impiega un certo tempo( in minuti) TA schematizzabile con
una v.a. gaussiana con parametri (102,9). Un secondo operaio impiega un tempo( in minuti) TB
B
schematizzabile con una v.a. gaussiana con parametri (100,16). I due operai inizano il lavoro
contemporaneamente ed in maniera indipendente.Quale è la probabilità che l’operaio A finisca il
lavoro prima dell’operaio B
La coppia di variabili TA e TA sono due una coppia di v.a. gaussiane indipendenti. Pertanto la
variabile D = TA - TA è ancora una v.a. gaussiana con parametri (8,25):
⎛− 2⎞
Pr{T A < TB } = Pr{(T A − TB ) ≤ 0} = Pr{D ≤ 0} = Φ⎜
⎟ ≈ 0.334
⎝ 5 ⎠
Esercizio 1.8
Si supponga che l’altezza(cm) di un gruppo molto numero sia una v.a gaussiana X ∈ N(170,100).
Mentre il peso(Kg) sia espresso da una v.a gaussiana Y ∈ N(75,100). Poiché le v.a. X e Y si
riferiscono allo stesso gruppo di persone sono correlate (ρ = 0.8) Quale è la probabilità che scelta
una persona a caso pesi meno di 75 Kg?. Quale il peso medio delle persone alte 180 cm? Quale
è la probabilità che una persona alta 180 cm pesi meno di 75 Kg?
La prima domanda riguarda soltanto la v.a. Y pertanto:
Pr{Y ≤ 75} = Φ (0 ) = 0.5
Modelli e Metodi per la Simulazione
La seconda domanda implica il calcolo del valor medio condizionato E[Y|X = 180]
E [Y X = 180] = μ Y + 0.8
σY
(180 − μ X ) = 75 + 0.8(180 − 170) = 83 Kg
σX
La deviazione standard della v.a. condizionata Y|X, vale:
(
)
σ Y2 X = σ Y2 1 − ρ 2 = 10 1 − 0.64 = 6
Quindi la risposta alla terza domanda è :
⎛ 4⎞
⎛ 75 − 83 ⎞
Pr{(Y X = 180) ≤ 75} = Φ⎜
⎟ = Φ⎜ − ⎟ ≈ 0.0912
⎝ 6 ⎠
⎝ 3⎠
15
16
Esercizi e Complementi
STIMA PER INTERVALLI
La stima per intervalli, consiste nel determinare se il valore del parametro θ da stimare ricade in un certo
intervallo, che viene definito intervallo di fiducia della stima. Il problema viene formulato nel seguente
modo
Pr{B1 < θ < B2 } = 1 − γ
Dove B1 e B2 sono due variabili statistiche, il cui valore è completamente determinato dal campione dati X,
B
B
mentre γ viene detto livello di incertezza.
Ricordiamo due risultati importanti della teoria della stima:
1) Quando il parametro da stimare è il valor medio μ di un campione dati gaussiano, la stima per
intervalli viene formulata nel seguente modo:
t1
t2
⎧
⎫
Pr ⎨ X −
S<μ<X +
S ⎬ = 1− γ
N −1
N −1 ⎭
⎩
dove X e S2 sono rispettivamente la media e la varianza campionaria. Le variabili B1 e B2 nel caso
B
specifico sono variabili t-Student con N – 1 gradi di libertà (N dimensione del campione).
2)Quando il parametro da stimare è la varianza del campione il problema viene formulato nel seguente
modo:
⎧ NS 2
NS 2 ⎫
Pr ⎨
<σ 2 <
⎬ = 1− γ
x1 ⎭
⎩ x2
I valori x1 e x2 si determinano facilmente dalle tavole del χ2 imponendo le condizioni:
{
}
Pr χ 2 ≥ x2 =
γ
2
{
}
Pr χ 2 ≥ x1 = 1 −
γ
2
Modelli e Metodi per la Simulazione
17
Esercizio 1.9
Dato un campione di dati X di dimensione N = 100, estratto da una popolazione avente scarto
quadratico medio σ = 5.1. Ipotizzando che la media campionaria sia X =21.6 costruire un
intervallo di fiducia al 95% per la stima del valor medio della popolazione.
L’esercizio consiste nel determinare un intervallo entro quale ritenere accettabile la stima del parametro μ,
con un livello di incertezza γ = 0.05. Poiché la varianza del campione è nota il problema può essere
formulato semplicemente nella forma:
Pr{z1 < μ < z 2 } = 0.95
Graficamente si ha la seguente situazione:
re g io n e d i
a c c e tta z io n e
re g io n e d i rifiu to
X
zγ
σ
μ
N
X + z
γ
σ
N
Per determinare la regione di accettazione [z1,z2] bisogna quindi calcolare la variabile zγ mediante la
conoscenza del livello di incertezza γ. Dalla tabella della distribuzione normale standard, si ricava:
{
}
[
]
Pr − z γ < Z < z γ = Φ ( z γ ) − 1 − Φ ( z γ ) = 2Φ ( z γ ) − 1 = 0.95 ⇒ Φ ( z γ ) = 0.975 ⇒ z γ = 1.96
Dal valore di zγ si ottiene il seguente intervallo di fiducia:
⎧
5 .1
5 .1 ⎫
σ
σ ⎫
⎧
< μ < X + zγ
< μ < 21.6 + 1.96
Pr ⎨ X − z γ
⎬ = Pr ⎨21.6 − 1.96
⎬ = 0.95 ⇒ 20.6 ≤ μ ≤ 22.6
10
10 ⎭
⎩
N
N⎭
⎩
18
Esercizi e Complementi
Esercizio 1.10
Considerato il campione dati X (N = 80), riportato in tabella, determinare un intervallo di
fiducia al 99% per la stima del valor medio.
15.8
26.4
17.3
11.2
23.9
24.8
18.7
13.9
9.0
13.2
22.7
9.8
6.2
14.7
17.5
26.1
12.8
28.6
17.6
23.7
26.8
22.7
18.0
20.5
11.0
20.9
15.5
19.4
16.7
10.7
19.1
15.2
22.9
16.6
20.4
21.4
19.2
21.6
16.9
19.0
18.5
23.0
24.6
20.1
16.2
18
7.7
13.5
23.5
14.5
14.4
29.6
19.4
17.0
20.8
24.3
22.5
24.6
18.4
18.1
8.3
21.9
12.3
22.3
13.3
11.8
19.3
20.0
25.7
31.8
25.9
10.5
15.9
27.5
18.1
17.9
9.4
24.1
20.1
28.5
L’esercizio è molto simile a quello precedente, bisogna però fare attenzione al fatto che questa volta la
varianza non è nota. La prima operazione da compiere è calcolare la media e la varianza campionaria:
X=
S2 =
1
N
1
N
N
∑x
i
= 18.8
i =1
N
∑ (x
i
− X ) 2 = 31.96
i =1
Il problema viene formulato nel seguente modo:
⎧
Pr ⎨ X −
⎩
tγ
N −1
S<μ<X +
⎫
S⎬ =1− γ
N −1 ⎭
tγ
(2 – 40)
Anche in questo caso il problema si riconduce al calcolo di una variabile tγ, mediante le tavole statistiche.
Questa volta bisogna utilizzare le tavole della distribuzione t-Student, poiché la varianza del campione dati
non è nota.
{
}
Pr − tγ < T < tγ = 1 − γ = 0.01
Poiché N = 80, è necessario conoscere la distribuzione t- Student con 79 gradi di libertà. Nella tabella a
disposizione, questo valore non è riportato. Quindi si può procedere in diversi modi, il primo è utilizzare il
Modelli e Metodi per la Simulazione
19
valore più vicino riportato nella tabella, e quindi dalla riga della distribuzione con 80 gradi di libertà si
legge tγ = 2.638, di conseguenza si ricavo l’intervallo:
⎫
⎧
2.638
2.638
Pr ⎨18.8 −
31.96 < μ < 18.8 +
31.96 ⎬ = 0.01 ⇒ 17.3 ≤ μ ≤ 20.47
79
79
⎭
⎩
Un secondo metodo è l’approssimazione gaussiana, tanto più valida quanto più grande è N. Per N = 79, è
ragionevole poter utilizzare tale approssimazione:
{
}
[
]
Pr − z γ < Z < zγ = Φ ( z γ ) − 1 − Φ ( z γ ) = 2Φ ( z γ ) − 1 = 0.99 ⇒ z γ = 2.5758
⎧⎪
31.96
31.96 ⎫⎪
Pr ⎨18.8 − 2.5758
< μ < 18.8 − 2.5758
⎬ = 0.99 ⇒ 17.1 ≤ μ ≤ 20.5
80 ⎪⎭
80
⎪⎩
Esercizio 1.11
Si consideri il seguente campione dati X (N = 15):
[0.060, 0.082, 0.056, 0.075, 0.091, 0.074, 0.072, 0.074, 0.080, 0.064, 0.068, 0.085, 0.078, 0.071]
Si determini un intervallo di fiducia al 95% per la stima del valor medio e della deviazione standard.
Calcolo della media e della varianza campionaria:
X=
S2 =
1
N
1
N
N
∑x
i
= 0.074
i =1
N
∑ (x
i
− X ) 2 = 0.000081
i =1
Per la stima del valor medio utilizziamo le tavole della distribuzione t-Student con 14 gradi di libertà,
poiché il livello di incertezza è γ = 0.05, si ha tγ = 2.145:
⎧
⎫
2.145
2.145
Pr ⎨0.074 −
0.009 < μ < 0.074 +
0.009⎬ = 0.05 ⇒ 0.069 ≤ μ ≤ 0.079
14
14
⎩
⎭
20
Esercizi e Complementi
Per la stima della varianza, si ha:
⎧ NS 2
NS 2 ⎫
2
Pr ⎨
<σ <
⎬ = 1− γ
x1 ⎭
⎩ x2
I valori x1 e x2 si determinano dalla tabella del χ2 facilmente imponendo le condizioni:
{
}
Pr χ 2 ≥ x 2 =
{
γ
}
Pr χ 2 ≥ x1 = 1 −
2
γ
2
Pertanto x2 = 26.119 e x1 = 5.629, da cui:
⎧⎪ NS 2
<σ <
Pr ⎨
⎪⎩ x 2
NS 2
x1
⎫⎪
⎧⎪
15 ⎫⎪
15
< σ < 0.009
⎬ = 1 − γ = Pr ⎨0.09
⎬ = 0.95 ⇒ 0.007 ≤ σ ≤ 0.015
5.629 ⎪⎭
26.119
⎪⎩
⎪⎭
Complemento 1.4
E’ importante notare, che se diminuisce il livello di incertezza γ, l’intervallo di fiducia aumenta. Questo
che apparentemente è un risultato positivo, deve far riflettere. Perché l’aumento della fiducia nella stima,
significa che la stima è poco attendibile, perché più è ampio l’intervallo in cui si cerca un parametro, e più
facile è trovarlo. Quindi una buona stima, è una stima con un livello di incertezza basso ed un intervallo di
fiducia molto stretto.
Modelli e Metodi per la Simulazione
21
TEST DI IPOTESI STATISTICHE
Si chiamano test di ipotesi statistiche (o prove d’accordo) tutti quei procedimenti atti a verificare, per
mezzo dello studio di campioni, se sono accettabili o meno delle ipotesi fatte sulla legge di distribuzione
di una variabile. Nella sua forma più generale il test delle ipotesi statistiche viene formulato nel seguente
modo:
‰ Si definisce una variabile H (funzione del campione dati X) detta statistica del test;
‰ Si definisce un intervallo di fiducia entro il quale devono essere verificate le ipotesi;
‰ Se in corrispondenza del particolare campione osservato la variabile H assume un valore esterno
all’intervallo di fiducia, l’ipotesi fatta viene rifiutata.
Quindi formalmente il problema viene formulato in maniera analoga al calcolo dell’intervallo di fiducia
per la stima dei parametri:
Pr{h1 < H < h2 } = 1 − γ
Se il valore di H, ottenuto dal campione in esame, cade all’interno dell’intervallo [h1,h2] non è ragionevole
rifiutare l’ipotesi, che può essere accetta con una certa cautela derivante dal livello di incertezza γ.
Un test molto importate è il test del χ2 (Chi-quadro), che viene utilizzato, per verificare se un campione
dati X osservato segue una distribuzione uniforme. Per condurre il test si suddivide l’intervallo della
variabile uniforme ipotizzata in s parti e si determina la variabile Ri che rappresenta il numero di elementi
del campione che assumono un valore compreso nella i-esima parte, i valori (R1, R2, R3, … RS).
Poiché sulla variabile in esame viene fatta l’ipotesi sulla sua distribuzione, in ogni intervallo dovrebbe
cadere un numero di valori pari a : (p1, p2, p3, …, pS). La statistica del test V viene calcolata nel seguente
modo:
V =
S
(Ri − Npi )2
i =1
Npi
∑
Fissato un certo livello di incertezza γ, dalle tabelle del χ2 con s-1 gradi di libertà, si può ricavare xγ tale
che
{
}
Pr χ 2 ≥ xγ = γ
22
Esercizi e Complementi
A questo punto possiamo formulare un test di ipotesi statistiche del tipo:
Pr {0 < V < xγ } = 1 − γ
dove l’intervallo [0, xγ] definisce la regione di accettazione. L’ipotesi verrà rifiutata se il valore di V
ottenuto da un particolare campione, è esterno alla regione di accettazione.
Esercizio 1.11
Gli incidenti di auto avvenuti in un anno su un tratto di strada sono indicati per ogni mese nella seguente
tabella:
MESE
GEN
FEB
MAR APR
MAG GIU LUG
AGO SET
OTT
NOV
DIC
n° incidenti
19
16
20
33
35
18
30
21
22
30
34
22
Si vuole provare con un livello di incertezza γ = 0.01, l’ipotesi che la probabilità evento incidente non
dipenda dal particolare mese in cui accada.
L’ipotesi che il numero di incidenti non dipenda dal mese, si traduce definendo una v.a. discreta X, che sia
uniformemente distribuita nell’intervallo [1,12], con vettore delle probabilità: p1,= p2,= p3,= …,= pS = 1/12.
Per verificare se il numero degli incidenti segua questa legge di distribuzione utilizziamo il test del χ2
definendo la variabile V:
S
(Ri − Npi )2
i =1
Npi
V =∑
L’intervallo dei definizione della distribuzione in esame, viene suddiviso chiaramente in dodici parti s=12
Al posto di Ri sostituiamo il relativo numero di incidenti nel relativo mese, mentre la dimensione del
campione si ottiene sommando tutti i valori della tabella:
12
N = ∑ Ri = 300 ⇒ Npi = 25
i =1
A questo punto siamo in grado di calcolare il valore di V:
Modelli e Metodi per la Simulazione
V=
12
(Ri − 25)2
i =1
25
∑
23
≅ 20.8
Dalle tabelle del χ2 ricaviamo xγ tale che:
{
}
Pr χ 2 ≥ xγ = γ = 0.01 ⇒ xγ = 24.72
Poiché V < xγ, l’ipotesi fatta è vera con un livello di fiducia pari al 99%.
Esercizio 1.12
Si supponga di effettuare 100 lanci con una moneta e di ottenere 45 volte testa. Verificare mediante il test
del χ2 che la moneta non sia truccata.
Se la moneta è perfettamente simmetrica la variabile X che esprime il risultato del lancio, può assumere
due valori con probabilità pari a pi = 0.5, i = 1,2. Associamo ad 1 il risultato testa e a 2 il risultato croce:
N=
2
∑R
i
= 100 ⇒ Np i = 50
i =1
V=
S
(Ri − Npi )2
i =1
Np i
∑
=
(45 − 50) 2 (55 − 50) 2
(5) 2
+
=2
=1
50
50
50
Dalle tabelle del χ2 con 1 grado di libertà, si ricava che xγ è sempre maggiore di 1, per ogni γ >0.3. Quindi
l’ipotesi di simmetria sulla moneta può essere accettata con un livello di incertezza pari a 0.3
24
Esercizi e Complementi
Esercizio 1.13
Si supponga di effettuare al calcolatore l’esperimento del lancio di un dado. L’esperimento viene ripetuto
120 volte ottenendo i seguenti risultati:
Valore
1
2
3
4
5
6
Risultato
25
17
15
23
24
16
Per poter verificare se la simulazione condotta riproduce fedelmente la realtà, analizziamo il risultati
ottenuti. Mediante il test del χ2 si vuole verificare che la sequenza di dati ottenuti sia uniforme
nell’intervallo [1,6] con un livello di incertezza γ = 5%
Questo tipo di verifica è molto frequente, nell’analisi degli Input di un simulazione. In pratica lo scopo è
verificare che la sequenza casuale generata al calcolatore segua la distribuzione desiderata. Nel caso
specifica bisogna verificare che la sequenza si uniforme nell’intervallo [1,6]
N=
6
∑R
i
= 120 ⇒ Np i = 20
i =1
V=
S
(Ri − Npi )2
i =1
Np i
∑
=
(25 − 20) 2 (17 − 20) 2 (15 − 20) 2 ( 23 − 20) 2 (24 − 20) 2 (16 − 20) 2
+
+
+
+
+
=5
20
20
20
20
20
20
Dalle tabelle del χ2 con 5 gradi di libertà ricaviamo xγ tale che:
{
}
Pr χ 2 ≥ xγ = γ = 0.05 ⇒ xγ = 11.071
Poiché V < xγ, l’ipotesi fatta è vera con un livello di fiducia pari al 95%.
Modelli e Metodi per la Simulazione
25
Esercizio 1.14
Durante l’esecuzione di una simulazione è previsto generare una sequenza di 250 numeri casuali tra
[0,9]. Per poter verificare la corretta generazione della sequenza casuale, viene suddiviso l’intervallo
[0,9] in 10 parti e si effettua il conteggio di quanti valori cadono nel singolo intervallo, e si ottiene la
seguente tabella:
Valore
0
1
2
3
4
5
6
7
8
9
Risultato
17
31
29
18
14
20
35
30
20
36
Mediante il test del χ2 si vuole verificare che la sequenza di dati ottenuti sia uniforme nell’intervallo [0,9]
Analogamente all’esercizio precedente:
N=
10
∑R
i
= 250 ⇒ Np i = 25
i =1
V=
S
(Ri − Npi )2
i =1
Np i
∑
=
10
(Ri − 25)2
i =1
25
∑
= 23.28
Poiché non viene fatta nessun riferimento al livello di incertezza scegliamo due valori γ = (5%,1%) Dalle
tabelle del χ2 con 9 gradi di libertà ricaviamo xγ tale che:
{
}
{
}
Pr χ 2 ≥ xγ = γ = 0.05 ⇒ xγ = 16.919
Pr χ 2 ≥ xγ = γ = 0.01 ⇒ xγ = 21.666
In entrambi i casi non è possibile accettare il test.
Se si analizza attentamente la tabella si vede che per γ =0.5%, si ottiene xγ = 23.589. Il test in questo caso
può essere accettato anche se lo scarto è minimo. E’ opportuno ricordare, che in questo caso è poco
significativo accettare il test, in primo luogo perché lo scarto è minimo, ma soprattutto perché l’ipotesi è
verificata con un livello di incertezza molto basso, e quindi con un intervallo di fiducia molto ampio.
Abbiamo più volte ribadito, che quando l’intervallo di fiducia è molto ampio è poco significativo accettare
un test di ipotesi statistiche.
26
Esercizi e Complementi
Esercizio 1.15
Nell’analisi dell’ accadimento di un certo evento, si è misurato che l’evento nelle ultime 90 settimane si è
verificato secondo il seguente campione dati:
N° di eventi per settimana
0
1
2
3 o più
N° di settimane in cui si è verificato
52
32
6
0
Dalla tabella, si evince che sono 52 le settimane in cui non si è verificato, mentre sono 32 le settimane in
cui si è verificato una volta, e 6 le settimane in cui si è verificato 2 volte, etc. Verificare mediante il test
del χ2 che la frequenza degli evento segua una distribuzione di Poisson con parametro λ = 0.4 con livello
di incertezza γ = 5%
L’esperimento in esame consiste nell’osservare, in un intervallo temporale ben definito (0,t) pari ad una
settimana il verificarsi di un dato evento. In generale ogni osservazione è indipendente dalle altre, e quindi
ogni occorrenza dell’evento è indipendente dalle altre, inoltre dai dati osservarti la frequenza delle
occorrenze dell’evento sembra piuttosto regolare Quindi è lecito supporre, che l’occorrenza di questo
evento segua una distribuzione di Poisson. Per calcolare i valori delle probabilità pi bisogna utilizzare la
formula di Poisson:
pn =
λn
n!
e −λ
da cui:
p0 =
0.4 0 −0.4
e
= 0.6703
0!
p1 =
0 . 4 1 − 0 .4
e
= 0.2681
1!
p2 =
0.4 2 −0.4
e
= 0.0536
2!
p 3 = 1 − ( p 0 + p1 + p 2 ) = 0.0080
Chiaramente nel nostro caso sebbene l’indice parte da zero (p0, p1, p2, p3), queste probabilità vanno lette
come (p1, p2, p3, p4) perché l’indice della sommatoria del calcolo della statistica del test V parte da 1:
Modelli e Metodi per la Simulazione
V=
3
∑
i =1
(Ri − Npi )2 (52 − 60.33)2 (32 − 24.13)2 (6 − 5.54)2
=
+
+
Np i
60.33
24.13
5.54
27
= 3.76
Le ultime due probabilità sono state accorpate, poiché la somma delle loro probabilità assolute è minore di
5 è quindi sono ininfluenti per il test (Np3 = 0.0536*90=4.824, Np4 = 0.0536*90=0.72) le abbiamo
sommate e considerate come un unico caso (Np3+4 = 5.54). Questa è una regola empirica per assicurarsi
che la statistica del test sia una v.a. del χ2.
Dalle tabelle del χ2 con 2 gradi di libertà ricaviamo xγ tale che:
{
}
Pr χ 2 ≥ xγ = γ = 0.05 ⇒ xγ = 5.991
Poiché V < xγ, l’ipotesi fatta è vera con un livello di fiducia pari al 95%.
Esercizio 1.16
Si ipotizza che il numero di difetti di presenti su un circuito stampato segue una legge di Poisson. Su un
campione di 60 circuiti presi a caso si misurano le seguenti frequenze di difetti:
N° difetti
0
1
2
3 o più
N° di circuiti in cui è sono presenti i difetti
32
15
9
4
Verificare mediante il test del χ2 che la frequenza degli evento segua una distribuzione di Poisson con
livello di incertezza γ = 5%
Poiché in questo caso non viene fatta nessuna ipotesi sul parametro della distribuzione utilizzimo un
valore stimato. Dalla teoria è noto che la media campionaria è corrisponde alla stima a massima
verosimiglianza del valor medio di un v.a. di Poisson, pertanto:
λˆ =
0 ⋅ 32 + 1 ⋅ 15 + 2 ⋅ 9 + 3 ⋅ 4
= 0.75
60
da cui:
28
Esercizi e Complementi
p0 =
0.75 0 −0.75
e
= 0.4724
0!
p1 =
0.751 −0.75
e
= 0.3543
1!
p2 =
0.75 2 −0.75
e
= 0.1329
2!
p 3 = 1 − ( p 0 + p1 + p 2 ) = 0.0404
Anche in questo caso conviene accorpare le ultime due probabilità. Questo si poteva anche vedere , dalla
tabella iniziale, infatti perché il test sia significativo, in ogni intervallo i-esimo, in cui si divide il campione
dati è bene che cadano al meno 10 valori. Unendo le ultime due colonne otteniamo : 9+4 =13
V=
3
∑
i =1
(Ri − Npi )2 (32 − 28.34)2 (15 − 21.26)2 (13 − 10.39)2
=
+
+
Np i
28.34
21.26
10.39
= 2.97
Poiché il valor medio della variabile di Poisson è stato stimato dal campione, non bisogna utilizzare la
distribuzione del χ2 con 2 gradi di libertà ( come si dovrebbe perché la statistica del test è stata calcolato
con s = 3), ma quella con un grado di libertà, perché bisogna anche considerare l’incertezza della stima
effettuata, quindi diminuire i gradi di libertà del numero di parametri stimati dal campione dati (in questo
caso solo il valor medio), pertanto ricaviamo xγ tale che
{
}
Pr χ 2 ≥ xγ = γ = 0.05 ⇒ xγ = 3.841
Poiché V < xγ, l’ipotesi fatta è vera con un livello di fiducia pari al 95%.
Modelli e Metodi per la Simulazione
29
Esercizio 1.17
Osservando gli arrivi in un centro di servizio, si registrano i seguenti valori:
0.87
2.57
3.23
3.94
0.06
0.95
2.48
1.43
1.63
15.80
1.50
1.36
3.43
0.25
1.04
5.53
0.54
1.41
2.68
0.80
3.86
2.23
2.00
1.88
2.73
0.17
0.01
0.55
3.48
0.77
che rappresentano i tempi di inter-arrivo delle richieste di servizio al sistema. Verificare mediante il test
del χ2 che la distribuzione dei tempi di inter-arrivo segua una legge esponenziale negativa.
Nell’analisi dei sistemi a coda, questo tipo di verifica è necessaria per poter decidere di adottare un
modello markoviano per descrive il sistema. Poiché abbiamo soltanto un campione dati X osservato senza
nessuna ipotesi calcoliamo la media e varianza campionaria:
X=
S=
1
N
N
∑x
1
N
i
= 2.31
i =1
N
∑ (x
i
− X ) 2 = 2.88
i =1
Se i tempi di inter-arrivo fossero esponenziali, ogni arrivo è indipendente dal precedente, è si può
ipotizzare che gli arrivi sono uniformemente distribuiti all’interno dell’intervallo di osservazione. Questo
significa che se suddividiamo la sequenza complessiva di 30 valori in s = 6 intervalli, in ogni intervallo
devono cadere 5 valori della sequenza. Se suddividiamo l’intervallo [0,1] in 6 parti otteniamo i seguenti
sottointervalli con i rispettivi valori di soglia:
5
5
5
5
5
5
* * * * * * * ** * * * ** *
* *** *
* ** * * * * * * *
0.00
0.167
0.333
0.500
0.667
0.883
1.00
30
Esercizi e Complementi
Il problema va trasportato ad una distribuzione esponenziale, quindi dobbiamo traslare i valori di soglia
secondo la formula:
E ( x ) = −2.31 ln[1 − U ( x )]
E contare in ogni intervallo quanti valori cadono:
4
5
6
5
* ** * ** ** * * * * * * * * *
0.00 0.421 0.935
1.599
* * *
2
8
* * ** * ** * *
2.534
4.133
*
15.95
chiaramente per effetto della trasformazione di variabile gli intervalli non sono della stessa lunghezza, ma
in ogni caso dovrebbero cadere 5 valori in ogni intervallo (ipotesi di uniformità). Poiché si osservano dei
valori diversi in ogni intervallo, effettuiamo il test del χ2 con un livello d’incertezza del 5% per verificare
l’ipotesi:
N=
6
∑R
i
= 30 ⇒ Np i = 5
i =1
V=
6
∑
i =1
(Ri − Npi )2 (4 − 5)2 (5 − 5)2 (6 − 5)2 (5 − 5)2 (8 − 5)2 (2 − 5)2
=
+
+
+
+
+
Np i
5
5
5
5
5
5
=4
Poiché abbiamo utilizzato, un valore stimato del valor medio della distribuzione esponenziale, bisogna
utilizzare la tavola del χ2 con 4 gradi di libertà:
{
}
Pr χ 2 ≥ xγ = γ = 0.05 ⇒ xγ = 9.488
Poiché V < xγ, l’ipotesi fatta è vera con un livello di fiducia pari al 95%.
NUMERI PSEUDO-CASUALI
GENERATORI DI SEQUENZE PSEUDO-CASUALI
Un generatore congruente lineare, ha la seguente espressione
X n+1 = (aX n + c)
mod m
Il parametro a è detto moltiplicatore mentre c incremento, m è il valore rispetto al quale si esegue
l’operazione di modulo. In particolare se c = 0, il generatore viene detto moltiplicativo. Il termine iniziale
dell’algoritmo X0 è detto seme ed è un numero intero. Per ottenere dalla sequenza numerica Xn una
sequenza di valori distribuita tra [0,1] è sufficiente la seguente operazione
Un =
Xn
m
La sequenza ottenuta è periodica al più di periodo m, in particolare si dice che ha periodo pieno se il suo
periodo è proprio m, e ciò si verifica quando sono verificate le seguenti condizioni:
‰ Se m e c sono primi tra loro;
‰ Se m è divisibile per un numero primo b, per il quale deve essere divisibile anche a – 1;
‰ Se m è divisibile per 4, allora anche a – 1 deve essere divisibile per 4.
Oltre a queste verifiche è necessario anche verificare l’uniformità della sequenza mediante l’istogramma
(analisi qualitativa) e mediante il test del χ2 (analisi quantitativa).
Dopo aver ottenuto una sequenza pseudo-casuale è possibile ottenere altre distribuzioni mediante le
trasformazioni di variabili aleatorie, o mediante il metodo della reiezione-accettazione.
Appare evidente che maggiore è il periodo della sequenza ottenuta, e maggiori sono le probabilità di aver
ottenuto un buon generatore. Poiché per ottenere un periodo molto elevato bisogna utilizzare valori di m
molto elevati, almeno m ≥ 235, e di conseguenza anche valori di a molto grandi, questo significa che
bisogna avere elaboratori elettronici con notevoli capacità di calcolo. Bisogna anche considerare lo scopo
per cui si svolge la simulazione, infatti se non sono necessarie sequenze molto numerose si possono
utilizzare anche generatori con valori più bassi.
32
Esercizi e Complementi
Esercizio 2.1
Dato il seguente generatore congruente lineare (LCG), calcolare la sequenza pseudo-randomica generata
e verificare l’uniformità,mediante la tecnica dell’istogramma. LCG = (a = 3, X0 = 3, m = 7).
Calcoliamo la sequenza Xn:
X1 = 3X 0
mod(7) = 2
X 2 = 3X1
mod(7) = 6
X 3 = 3X 2
mod(7) = 4
X 4 = 3X 3
mod(7) = 5
X 5 = 3X 4
mod(7) = 1
X 6 = 3X 5
mod(7) = 3
X 7 = 3X 6
mod(7) = 2
Un =
Xn
= [0.285 0.857 0.571 0.142 0.428 0.428 0.285]
7
suddividiamo l’intervallo [0,1] in 6 intervalli e contiamo quanti valori cadono in ogni singolo intervallo:
I= [0, 0.167, 0.333, 0.500, 0.667, 0.833, 1]
R = [2, 2, 1, 1, 0, 1]
2
1.8
1.6
1.4
1.2
1
0.8
0.6
0.4
0.2
0
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
Modelli e Metodi per la Simulazione
33
Esercizio 2.2
Ripetere l’esercizio precedente con m = 14
Calcoliamo la sequenza Xn:
X 1 = 3X 0
mod(14) = 9
X 8 = 3X 7
mod(14) = 13
X 2 = 3X 1
mod(14) = 13
X 9 = 3X 8
mod(14) = 11
X 3 = 3X 2
mod(14) = 11
X 10 = 3 X 9
mod(14) = 5
X 4 = 3X 3
mod(14) = 5
X 11 = 3 X 10
mod(14) = 1
X 5 = 3X 4
mod(14) = 1
X 12 = 3 X 11
mod(14) = 3
X 6 = 3X 5
mod(14) = 3
X 13 = 3 X 12
mod(14) = 9
X 7 = 3X 6
mod(14) = 9
X 13 = 3 X 14
mod(14) = 13
Un = [0.6429, 0.9286, 0.7857, 0.3571, 0.0714, 0.2143, 0.6429, 0.9286, 0.7857, 0.3571, 0.0714,
0.2143, 0.6429, 0.9286]
R = [4, 2, 0, 3, 2, 3]
4
3.5
3
2.5
2
1.5
1
0.5
0
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
Il risultato non è molto incoraggiante, quindi la scelta di aumentare il periodo non basta per migliorare, il
generatore, infatti abbiamo ottenuto una sequenza con un periodo molto basso, infatti il numero primo per
cui è divisibile m è 7, mentre a-1 non è divisibile per 7.
34
Esercizi e Complementi
Esercizio 2.3
Dato il seguente generatore congruente lineare (LCG: a = 17, c = 43, X0 = 27, m = 100), verificare al
calcolatore, l’uniformità mediante la tecnica dell’istogramma e il test del χ2 con un livello di incertezza
del 5%
Prima di generare la sequenza al calcolatore bisogna fare alcune verifiche preliminari sui parametri del
LCG:
‰ Se m e c sono non hanno divisori comuni, sebbene m non sia un numero primo;
‰ Sia m = 100 che a – 1 = 16 sono divisibili per 2 (numero primo)
‰ Sia m = 100 che a – 1 = 16 sono divisibili per 4
Quindi possiamo concludere che la sequenza generata avrà periodo pieno. Di seguito riportiamo i primi 3
(la sequenza completa ha lunghezza N = 100):
X n+1 = (aX n + c)
mod m
X1
= 0.02
m
X 1 = 17 X 0 + 43
mod(100) = 2 ⇒ U 1 =
X 2 = 17 X 1 + 43
mod(100) = 77 ⇒ U 2 =
X2
= 0.77
m
X 3 = 17 X 2 + 43
mod(100) = 53 ⇒ U 3 =
X3
= 0.52
m
Per implementare il test del χ2 è possibile suddividere l’intervallo [0,1] in s = 10 parti, per ognuna di
queste parti pi = 0.1:
N=
10
∑R
i
= 100 ⇒ Np i = 10
i =1
Il vettore delle variabili Ri = [25, 0, 0, 25, 0, 0, 25, 0,0, 25]
Poiché ci sono geli intervalli in cui non cadono valori, effettuiamo l’aggregazione, calcolando il test su 4
con 25 valori:
Modelli e Metodi per la Simulazione
V=
4
∑
i =1
(Ri − Npi )2 (25 − 25)2 (25 − 25)2 (25 − 25)2 (25 − 25)2
=
+
+
+
Npi
25
25
25
25
35
=0
Mediante la tavola del χ2 con 3 gradi di libertà:
{
}
Pr χ 2 ≥ xγ = γ = 0.05 ⇒ xγ = 7.185
Poiché V < xγ, l’ipotesi fatta è vera con un livello di fiducia pari al 95%. Bisogna in questo caso fare
attenzione perché il test del χ2 condotto in questo modo è falsato. Infatti osservando il vettore Ri è
possibile notare che ci sono degli intervalli in cui sono concentrati molti valori, ed altri vuoti, questo basta
per concludere che la sequenza generata non può essere utilizzata come sequenza pseudocasuale in una
simulazione perché il generatore LCG scelto non è affidabile:
25
20
15
10
5
0
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
Istogramma della sequenza casuale di 100 con s =10
Questo esercizio mette in risalto un forte limite del test del χ2 , quando viene utilizzato per verificare il
comportamento di un generatore LCG per questo motivo, la verifica si accompagna molto spesso con
l’istogramma e ad altri tipi di verifiche più significative che saranno illustrate nelle pagine seguenti.
36
Esercizi e Complementi
Esercizio 2.4
Data la seguente sequenza di numeri pseudocasuali Un = [0.44, 0.81, 0.14, 0.05, 0.93] verificare
l’uniformità mediante il test di Kolmogorov-Smirnov con un livello di incertezza pari al 5%
Il campione dati disponibile è molto piccolo ( N = 5), quindi il test del χ2 non può essere condotto in
maniera significativa. In questo caso si preferisce il test KS:
La prima operazione da compiere è ordinare i valori del campione osservato:
F 0 (0.05) = 0.20, F 0 (0.14) = 0.40 F 0 (0.44) = 0.60 F 0 (0.81) = 0.80 F 0 (0.93) = 1
E’ opportuno ricordare che una variabile aleatoria che segue una legge di distribuzione uniforme
nell’intervallo [0,1] è descritta dalle seguenti curve:
F(x)
f(x)
X
X
1
1
0
1
x
0
Densità di
Probabilità
1
x
Distribuzione di
Probabilità
Per implementare il test KS bisogna utilizzare la curva Distribuzione di Probabilità (la curva di destra):
F 0 ( X (i ) )
FX ( X (i ) )
F 0 ( X ( i ) ) − FX ( X ( i ) )
0.20
0.05
0.15
0.40
0.14
0.26
0.60
0.44
0..16
0.80
0.81
0.01
1.00
0.93
0.07
Il punto di massima distanza dalla curva ipotizzata è il 2° della tabella quindi X(2) = 0.14, per cui la
statistica del test è D = 0.26. Se poniamo un livello di incertezza pari a γ = 0.05, le tabelle (K – S) curva
Modelli e Metodi per la Simulazione
37
forniscono per N = 5, un valore dγ = 0.56, poiché la statistica del test D è minore di questo valore, l’ipotesi
fatta (sequenza osservata uniforme) può essere accettata.
Tes t di K olm ogorov-S m irnov
1
0.9
0.8
Curva os servata ->
0.7
< - Curva teoric a
F(x )
0.6
0.5
0.4
0.3
0.2
0.1
0
0
0.1
0.2
0.3
0.4
0.5
x
0.6
0.7
0.8
0.9
1
Interpretazione grafica del test di Kolmogorov-Smirnov
Complemento 2.1
Il test di Kolmogorov-Smirnov, a differenza del test del χ2, analizza la forma della legge di distribuzione,
pertanto è più potente nel caso di campioni con pochi valori. Il test del χ2 è più idoneo ad analizzare la
densità dei punti all’interno degli intervalli in cui suddividiamo l’intervallo di definizione della variabile, e
molto spesso è necessario accompagnare questo test mediante un’analisi fatta con l’istogramma. Quando
la sequenza pseudocasuale è molto numerosa il test KS diventa molto laborioso ma con l’attuale
disponibilità di calcolatori elettronici, è possibile implementare entrambi i test al calcolatore, pertanto
quando si genera una sequenza pseudocasuale uniforme, è consigliabile effettuare tutte le verifiche prima
di accettare il generatore ed utilizzarlo per una simulazione.
38
Esercizi e Complementi
Complemento 2.2
La verifica dell’uniformità della sequenza pseudocasuale non è l’unica verifica da effettuare, per accettare
un LCG. Una verifica molto importante e necessaria è quella della correlazione tra i valori della sequenza.
Questo tipo di verifica è molto più complessa, ma è necessaria perché un generatore LCG che supera i test
di uniformità non può essere utilizzato se i valori della sequenza non sono incorrelati. Questa condizione
non si può ottenere e quindi è sufficiente che la correlazione sia molto bassa. Un test molto potente che
viene condotto per verificare la bontà dei generatori LCG è il test spettrale, che sfrutta una particolare
proprietà dei generatori LCG. Questi generatori presentano una struttura a reticolo, se ad esempio
suddividiamo la sequenza in triple, ed analizziamo la disposizione dei valori in uno spazio tridimensionale
osserviamo una figura del tipo:
Generatore moltiplicativo IBM RANDU( LCG: a = 65539, c = 0, X0 = 1, m = 231), 1968
Il generatore LCG in figura è noto come RANDU, ed è stato implementato dalla IBM sui propri sistemi
nel 1968.
Come si vede dalla figura, i valori della sequenza si dispongono su dei piani ( questa è una diretta
conseguenza della struttura a reticolo dei generatori congruenti lineari). Se i piani non sono equidistanti,
significa che vi sono delle zone dell’intervallo [0,1] a maggiore densità di valori, e soprattutto che c’è una
elevato correlazione tra i valori della sequenza. Pensiamo ad esempio ad un generatore che simuli il lancio
del dado, se prendiamo i risultati a valori singoli è auspicabile che ogni valore abbia una percentuale pari
ad 1/6, mentre se prendiamo i valori della sequenza a coppie desideriamo che ogni coppia abbia una
percentuale pari a 1/36 e cosi via. Da questa considerazione nasce l’idea di verificare la correlazione e
l’uniformità della sequenza mediante la distanza tra i piani di cui è formato il reticolo. Se l’analisi è
condotta su due dimensioni i piani si riducono a delle rette, mentre se l’analisi viene condotta per
dimensioni k > 3, i piani diventano degli iperpiani non più rappresentabili graficamente, ma in ogni caso la
Modelli e Metodi per la Simulazione
39
distanza è calcolabile. Il test spettrale, consiste nel calcolare per ogni dimensione k > 1, la distanza
minima tra i paini e di effettuare una normalizzazione tale che si ottiene una variabile 0<S<1. Se S è molto
vicino ad 1, la correlazione è abbastanza bassa perché gli iperpiani sono quasi equidistanti, se invece S è
molto vicino a zero allora ci degli iperpiani molto vicini tra loro e quindi la sequenza generata ha una
elevata correlazione. Un risultato molto interessante del test spettrale, è che S non ha lo stesso valore per
tutte le dimensioni. Di seguito si riportano alcuni esempi di LCG molto comuni ed i rispettivi test spettrali.
LCG: a = 477211307, c = 0, X0 = 1, m = 232
Il test spettrale è stato condotto fino ad 8 dimensioni (k = 8) con il seguente risultato:
k
2
3
4
5
6
7
8
S
0.6581
0.0095
0.0500
0.1367
0.2608
0.4103
0.5660
Questo generatore analizzato in 2 dimensioni sembra buono, ma poi presenta un’elevata correlazione già
per valori della sequenza distanti più di due valori (k > 3). Graficamente:
Sui generatori LCG vengono fatte numerose prove ed poiché questi generatori dipendono molto
dai loro parametri tanto che un piccolo cambiamento di uno di essi può provocare la totale
modifica della sequenza generata il parametri (a, c, X0, m) vengono nella pratica determinati in
maniera esaustiva ripetendo per ogni scelta, il test spettrale ed i test di uniformità.
40
Esercizi e Complementi
Unix ANSI-C : LCG: a = 1103515245, c = 12345, X0 = 12345, m = 231
Il test spettrale è stato condotto fino ad 8 dimensioni (k = 8) con il seguente risultato:
k
2
3
4
5
6
7
8
S
0.84
0.52
0.63
0.49
0.68
0.43
0.54
BCSLIB: LCG: a = 515, c = 0, X0 = 1, m = 235
Implementato nel linguaggio SIMULA :
k
2
3
4
5
6
7
8
S
0.5809
0.4145
0.8004
0.6401
0.6951
0.6379
0.7473
Modelli e Metodi per la Simulazione
APPLE: LCG: a = 513, c = 0, X0 = 1, m = 235
Implementato da Apple Computers :
k
2
3
4
5
6
7
8
S
0.4746
0.3715
0.6376
0.6124
0.7416
0.6781
0.7473
Fishman-Moore: LCG: a = 742938285, c = 0, X0 = 1, m = 231-1
Implementato da Apple Computers :
k
2
3
4
5
6
7
8
S
0.8672
0.8607
0.8627
0.8319
0.8340
0.6239
0.7067
41
42
Esercizi e Complementi
Complemento 2.3
Un’altra importante classe di generatori di sequenze pseudocasuale è costituita dai generatori congruenti
inversi denominati ICG (proposti da Euchenauer e Lehr nel 1986), la cui formula è:
X n +1 = (a
1
+ c)
Xn
Un =
mod m
Xn
m
Questa classe di generatori è molto meno sensibile alla variazione dei parametri rispetto ai generatori
LCG. Purtroppo non avendo una struttura regolare non è possibile implementare il test spettrale, possiamo
in ogni caso analizzare una figura bidimensionale che ci dà una misura della correlazione, prendendo i
punti a coppia e disponendoli su di un piano. Questa operazione è analoga a quella vista in precedenza per
i generatori LCG, per i quali è stato possibile misurare la correlazione grazie alla struttura a reticolo ( che
in un piano ha come effetto di disporre le coppie di valori su delle rette parallele), per un generatore ICG
si ottiene una figura del tipo:
Oltre ai classici test illustrati, esistono molti altri tipi di test empirici che si effettuano sui generatori di
sequenze pseudocasuali per verificarne le prestazioni: come ad esempio verificare che un generatore
uniforme simuli correttamente delle variabili aleatorie indipendenti ed identicamente distribuite in [0,1]
Modelli e Metodi per la Simulazione
43
SEQUENZE PSEUDO-CASUALI NON UNIFORMI
La generazione di sequenze pseudocasuale uniformi in[0,1], è soltanto il primo passo della generazione di
numeri casuali. Infatti una volta ottenuta una sequenza che simuli in maniera accettabile una v.a. uniforme
in [0,1] bisogna determinare delle sequenze che rappresentino bene anche altre variabili aleatorie. Esistono
diverse tecniche per ottenere variabili aleatorie con densità di probabilità nota da una sequenza numerica
pseudocasuale. Negli esercizi proposti di seguito saranno illustrati alcuni esempi.
Esercizio 2.5
Data una sequenza di numeri pseudocasuali Un in [0,1], determinare una sequenza di numeri
pseudocasuale che segua una distribuzione uniforme in [b,b+a]
Consideriamo la seguente variabile Y
Y = aU + b
la funzione inversa è :
U = g −1 (Y ) =
Y −b
a
Quindi la distribuzione della v.a. uniforme in [a,b]:
⎧0
⎪⎪ y
FY ( y ) = ⎨
⎪a
⎪⎩ 1
−∞< y<b
b< y<b+a
y>b
44
Esercizi e Complementi
Esercizio 2.6
Data una sequenza di numeri pseudocasuali Un in [0,1], determinare una sequenza di numeri
pseudocasuale che segua una distribuzione esponenziale negativa
Indichiamo con E la v.a. esponenziale, e riflettiamo sulla seguente legge di corrispondenza:
E = − ln(1 − U )
la funzione inversa è :
U = g −1 ( E ) = 1 − e − E
Quindi la distribuzione della v.a. esponenziale:
FE ( y ) = 1 − e − y y ≥ 0
Sebbene siamo ceri di aver utilizzano un generatore molto affidabile per generare la sequenza
pseudocasuale Un conviene sempre effettuare dei test di verifica, come il test del χ2 oppure il test di
Kolmogorov-Smirnov per verificare che la v.a. generata segua la curva desiderata, molto semplice è
sufficiente una verifica mediante istogramma:
600
500
400
300
200
100
0
0
1
2
3
4
5
6
7
8
Modelli e Metodi per la Simulazione
45
Esercizio 2.7
Data una sequenza di numeri pseudocasuali Un in [0,1], determinare una sequenza di numeri
pseudocasuale che segua una distribuzione di Weibull con parametri (β,δ )
Questo esercizio è molto simile al precedente. La funzione densità di probabilità della v.a. di
Weibull è:
f X ( x) = e
β
⎛x⎞
−⎜ ⎟
⎝δ ⎠
β
δ
⎛x⎞
⎜ ⎟
⎝δ ⎠
β −1
La funzione distribuzione di probabilità vale:
FX ( x) = 1 − e
β
⎛x⎞
−⎜ ⎟
⎝δ ⎠
ponendo
U = g −1 ( X ) ⇒ X = δ [− ln(1 − U )] β
1
Confrontiamo l’istogramma con parametri (δ = 1, β = 2) con la curva reale (δ = 1, β = 2) per un’analisi
qualitativa, ma è possibile anche effettuare analisi più consistenti mediante il test del χ2 oppure il test di
Kolmogorov-Smirnov:
Densità di probabilità della v.a. di W eibull
250
1.8
1.6
200
1.4
b=0.8
1.2
150
f(x )
1
0.8
100
0.6
b=2
b=1
0.4
50
0.2
0
0
0
0.5
1
1.5
2
2.5
3
0
0.5
1
1.5
2
x
2.5
3
3.5
4
46
Esercizi e Complementi
Complemento 2.4
Con il metodo della trasformazione di variabili aleatorie è possibile anche generare variabili aleatorie
gaussiane. Osservando la probabilità congiunta di due v.a. gaussiane indipendenti X e Y si ha:
⎛ x2 + y 2
⎜
2
1 −⎜⎝
f XY ( x, y ) = f X ( x) f Y ( y ) =
e
2π
⎞
⎟
⎟
⎠
Consideriamo la seguente trasformazione in coordinate polari:
R = X 2 +Y2
⎛Y ⎞
Θ = arctan g ⎜ ⎟
⎝X⎠
Le variabili X e Y si ottengono dalle variabili R e Θ mediante la seguente trasformazione inversa:
X = R cos Θ
Y = R sin Θ
La densità di probabilità congiunta di R e Θ è:
r
f RΘ (r , θ ) =
e
2π
⎛ r2
−⎜
⎜ 2
⎝
⎞
⎟
⎟
⎠
con le singole densità di probabilità marginali :
f R (r ) = re
f Θ (θ ) =
⎛ r2
−⎜
⎜ 2
⎝
1
2π
⎞
⎟
⎟
⎠
r≥0
0 ≤ θ ≤ 2π
Modelli e Metodi per la Simulazione
47
In definitiva R è una variabile aleatoria di Rayleigh mentre Θ è una variabile aleatoria uniforme in [0,2π].
Poiché siamo in grado di generare solo variabili aleatorie uniformi in [0,1] il nostro obiettivo è di
manipolare le espressioni appena calcolate per ricavare una legge di trasformazione che permetta di
ricavare le v.a. gaussiane X e Y da v.a. uniformi U in [0,1]. La densità di Rayleigh è una legge
esponenziale quindi è molto semplice verificare che dalla distribuzione di probabilità di R:
r
FR (r ) =
∫f
R ( r )dr
=1− e
⎛ r2
−⎜
⎜ 2
⎝
⎞
⎟
⎟
⎠
r≥0
0
si ricava la seguente trasformazione, che permette di esprimere una v.a. R di Rayleigh in funzione di una
v.a. uniforme in [0,1] :
R = − 2 ln (1 − U )
la variabile Θ è uniforme in [0,2π], e nell’esercizio 2.5 abbiamo visto come si operano le trasformazioni di
v.a. uniformi, quindi definite due v.a. uniformi in [0,1] U1 e U2 la trasformazione che consente di ottenere
due v.a. gaussiane indipendenti X e Y è:
X = − 2 ln (1 − U 1 ) cos(2πU 2 )
Y = − 2 ln (1 − U 1 ) sin (2πU 2 )
48
Esercizi e Complementi
SEQUENZE PSEUDO-CASUALI DISCRETE
La generazione di variabili aleatorie discrete è molto semplice, basta ricordare la definizione di una v.a. di
Bernoulli. Questa v.a. può assumere solo due valori 0 ed 1, rispettivamente con probabilità (1 – p)
e p. L’idea è quella di determinare una regola che ci aiuti a passare da una variabile continua
uniforme in [0,1] alla v.a. di Bernoulli. Se fissiamo un valore di soglia pari a p ed eseguiamo un
test definendo una variabile B tale che:
⎧0 U > p
B=⎨
⎩1 U ≤ p
Otteniamo una v.a. di Bernoulli. Allo stesso modo si procede per qualsiasi v.a. discreta come vedremo
negli esercizi che seguono.
Esercizio 2.7
Data una sequenza di numeri pseudocasuali uniforme in [0,1] U, determinare una sequenza di numeri
pseudocasuale che segua una distribuzione discreta pn = [0.5, 0.3, 0.2]
La v.a discreta definita nella traccia dell’esercizio può assumere solo tre valori [0,1,2] e rispettivamente
con probabilità p0 = 0.5, p1 = 0.3, p2 = 0.2, partendo da una v.a. uniforme si può ottenere semplicemente
con seguente test:
⎧ 0 0 < U ≤ 0.5
⎪
Bn = ⎨1 0.5 < U ≤ 0.8
⎪ 2 0.8 < U ≤ 1
⎩
Modelli e Metodi per la Simulazione
49
Esercizio 2.8
Data una sequenza di numeri pseudocasuali uniforme in [0,1] U, determinare una sequenza di numeri
pseudocasuale che segua una distribuzione binomiale con parametri p e N
La v.a Binomiale ha funzione massa di probabilità:
⎛N⎞
p n = ⎜⎜ ⎟⎟ p n q ( N − n )
⎝n⎠
p + q =1
Massa di probabilità della v.a. binomiale
0.35
0.3
0.25
Pn
0.2
0.15
0.1
0.05
0
0
2
4
6
8
10
12
14
16
18
Xn
Massa di probabilità della v.a. Binomiale per N=15, p=0.8
Ed esprime la probabilità che un evento si realizzi n volte in un esperimento ripetuto N volte. Per N = 1, la
v.a. binomiale si riduce ad una v.a. di Bernoulli. Questo ci suggerisce di generare una v.a. di Bernoulli e di
ripetere l’esperimento N e contare il numero di volte che si verifica l’evento favorevole. Un possibile
algoritmo è riportato di seguito:
Binomiale (N,p)
for i=1:100
sum=0;%inizializzazione
for j=1:N
if(U < p);%generazione di una v.a. di Bernoulli
sum=sum+1;
end
end
B=sum+1;%B rappresenta una v.a. Binomiale
h(B)=h(B)+1;%compilazione dell’istogramma
end
50
Esercizi e Complementi
Esercizio 2.9
Data una sequenza di numeri pseudocasuali uniforme in [0,1] U, determinare una sequenza di numeri
pseudocasuale che segua una distribuzione geometrica con parametro p
La v.a. discreta geometrica è definita come il numero di prove k da effettuare prima che si abbia l’evento
favorevole, il quale ha probabilità p di accadere.
prove) = p(1 − p) k
Pr( successo dopo k
Massa di probabilità della v.a. geometrica
0.35
0.3
0.25
Pn
0.2
0.15
0.1
0.05
0
0
1
2
3
4
5
Xn
6
7
8
9
10
- Distribuzione geometrica (k = 10, p = 0.3)
Quindi per generare una v.a. geometrica basta semplicemente, generare una v.a. U, definire
l’evento favorevole come: U < p e contare il numero prove del test fino al primo evento
favorevole (ricordiamo che il primo campione della v.a. geometrica vale p: p0 = p).
for i=1:1000
geo= 0; %initializione
while U>p & geo+1<k
%stepping through the distribution
geo=geo+1; %geo è la v.a. geometrica
end
h(geo+1)=h(geo+1)+1; %compiliazione istogramma
end
La v.a. geometrica è definita per n = 0,1,…,∞. In realtà la sequenza viene generata per un numero
finito di valori k. Poiché la somma di tutti elementi della sequenza deve essere 1, è possibile
soprattutto negli ultimi termini (coda della distribuzione) che i valori della sequenza generata non
coincidano con quella teorica.
Modelli e Metodi per la Simulazione
51
Complemento 2.5
Alle volte per generare una v.a. discreta occorre esaminare attentamente le sue proprietà. Ad esempio la
v.a. di Poisson ha funzione massa di probabilità:
pn =
λn
n!
e −λ
Massa di probabilità della v.a. di Poisson
0.25
0.2
Pn
0.15
0.1
0.05
0
0
2
4
6
8
10
Xn
12
14
16
18
20
Massa di probabilità di una v.a. binomiale negativa con λ = 7
Partire dalla funzione massa di probabilità per generare la v.a. può essere complicato, quindi è opportuno
sfruttare alcune proprietà. Ad esempio una proprietà molto importante di cui gode una v.a. di Poisson è la
proprietà dell’uniformità degli eventi. Tutti gli eventi che si susseguono nell’intervallo di osservazione
(0,t) hanno inter-tempi esponenziali, quindi indicando con ei una successione di v.a. esponenziali con
valor medio 1/λ si ha:
n
∑
ei ≤ t <
i =1
n +1
∑e
i
i =1
il valore di n esprime il numero di eventi accaduti nell’intervallo (0,t) e quindi segue una distribuzione di
Poisson. Ricordando l’espressione che lega la v.a. esponenziale a quella uniforme, si può generare la v.a.
di Poisson direttamente da sequenze uniformi in [0,1] Ui
n +1
∏
i =1
U i < e − λt ≤
n
∏U
i =1
i
METODO MONTE CARLO
CALCOLO INTEGRALE
Il metodo Monte Carlo consiste nel ripetere numerose volte un esperimento per conteggiare il numero di
volte che si verifica un evento (un particolare risultato dell’esperimento) rispetto al numero totale di volte
che si ripete l’esperimento. In questo modo è possibile calcolare una stima della probabilità dell’evento:
Pr{ε } =
N (ε )
N tot
Dove con N(ε) abbiamo indicato il numero di volte che si verifica l’evento ε.
Questo metodo è molto usato nei problemi, ove si conosce una formulazione matematica, ma non riesce a
determinare una soluzione per via analitica. Il metodo Monte Carlo, può essere impiegato sia in problemi
di natura probabilistica, e sia in problemi di natura non aleatoria. Infatti grazie al forte impulso che ha
avuto l’informatica negli ultimi decenni, e alla possibilità di generare variabili casuali al calcolatore, negli
ultimi decenni questo metodo è stato molto impiegato per determinare soluzioni approssimati di equazioni
non risolvibili per via analitica. L’idea che è alla base, nasce dalla relazione integrale che definisce la
probabilità di un evento:
Pr{ε } = Pr{X (ε ) ≤ x} =
x
∫f
X
( x) dx
−∞
Da un esperimento definito su uno spazio campione Ω, è sempre possibile definire una variabile aleatoria
X con funzione di densità di probabilità fX(x), tale che la probabilità dell’evento ε, possa essere
determinata mediante il calcolo di un integrale definito. Questo significa calcolare la probabilità di un
evento mediante il calcolo di un’area.
1
0
1
Modelli e Metodi per la Simulazione
53
La possibilità di generare sequenze pseudo-casuali al calcolatore suggerisce di risolvere il problema
inverso, cioè conoscendo la probabilità di un determinato evento stabilire la stima dell’area a cui
corrisponde. Come si vede dalla figura, per calcolare l’area tratteggiata, è necessario risolvere un integrale
definito
x2
A=
∫ f ( x)dx
x1
che può essere molto complicato da risolvere per via analitica. Mediante il metodo Monte Carlo è
possibile generare delle sequenze pseudo-casuali, è contare quanti di questi valori cadono nell’area di
interesse, in questo modo si ottiene una stima dell’area cercata. Poiché questo procedimento è una vera e
propria simulazione utilizzata per ottenere un risultato che non è possibile ottenere per altre vie, bisogna
fare attenzione ad alcuni aspetti. In particolare considerare quelle operazioni necessarie in tutte le
simulazioni:
‰ Analisi degli Input
‰ Analisi degli Output
In questo tipo di simulazione l’input è costituito delle sequenze pseudo-casuali generate al calcolatore,
quindi occorre verificare la bontà delle sequenze affinché il risultato non sia falsato proprio da dati di
input non corretti. L’analisi degli output è necessaria per analizzare correttamente le variabili di stima per
ottenere un risultato quanto più vicino a quello reale.
Chiaramente questo procedimento può essere esteso anche agli integrali di superficie e agli integrali di
volume, in questo caso bisogna fare molta attenzione ai generatori LCG, poiché la disposizione sui piani
dei valori delle sequenze generate, potrebbe vanificare la simulazione. Infatti la struttura a reticolo dei
LCG, ha come conseguenza che delle regioni dello spazio sono più dense di punti di altre, e questo
potrebbe condurre ad una stima errata del volume d’interesse. Per questo motivo prima di utilizzare un
generatore LCG, per il calcolo dei volumi è necessario condurre il test spettrale sulla sequenza generata.
Quanto detto chiaramente può essere esteso al calcolo di ipervolumi di N dimensioni. Infine è importante
notare che le variabili di stato dei sistemi studiati nelle applicazioni scientifiche ed industriali sono sempre
esprimibili mediante relazioni integrali più o meno complesse, pertanto stimare il loro valore mediante la
simulazione ci riconduce quasi sempre al problema del calcolo di ipervolumi mediante il metodo Monte
Carlo.
54
Esercizi e Complementi
Esercizio 3.1
Determinare una stima del valore di π mediante il metodo Monte Carlo
Poiché l’area del cerchio vale A = πr2, possiamo considerare un cerchio di raggio unitario sul piano
cartesiano, o meglio il settore circolare del primo quadrante. Generando due v.a. uniformi in [0,1]: X, Y,
possiamo contare il numero di punti tali che: X2 + Y2 < 1:
π
4
1
-1
1
-1
Bisogna scegliere la lunghezza delle sequenze M, ed il numero di volte che si ripete la simulazione N. In
questo modo si ottiene una sequenza di Output A di N valori:
A = [a1 , a 2 , K a N ]
Ogni singolo valore ai è ottenuto dividendo il numero di valori che appartengono all’area, per M. Ed il
valore stimato dell’area sarà la media campionaria della sequenza A.
Effettuando la simulazione per M = 100, ed N = 10 si ottiene la seguente sequenza di Output:
A = [ 0.79, 0.78, 0.77, 0.82, 0.71, 0.79, 0.74, 0.77, 0.74, 0.78].
1
Aˆ =
N
N
∑A
i
i =1
mentre:
π
4
= 0.7854
= 0.7690
Modelli e Metodi per la Simulazione
55
Complemento 3.1
La stima ottenuta non è molto soddisfacente. Per cercare di capire il perché è necessario condurre l’analisi
degli Input delle sequenze generate, in questo caso bisogna effettuare i test per verificare l’uniformità,
quindi il test del χ2 e l’istogramma. Mentre per gli Output è necessario verificare che la sequenza di uscita
sia un campione dati gaussiano (test di Kolmogorov-Smirnov). Infatti in questo modo siamo sicuri che la
media campionaria calcolata sia la stima a massima verosimiglianza dell’area cercata. Inoltre bisogna
anche verificare che la varianza della sequenza di output sia molo piccola e che diminuisca all’aumentare
di N. Poiché per una buona simulazione occorre generare un numero elevato di punti, è necessario
implementare i test al calcolatore. Ad esempio eseguendo la simulazione dell’esercizio 3.1 si ottengono i
seguenti istogrammi per gli Input:
120
120
100
100
80
80
60
60
40
40
20
20
0
0
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
Istogramma delle sequenze X e Y con M = 1000
Per quantificare l’analisi occorre eseguire il test del χ2. Poiché la simulazione viene eseguita più volte, nel
nostro caso N volte, il test del χ2 andrebbe eseguito ad ogni run della simulazione. In questo modo per
ogni sequenza di Input si ottiene un vettore di N elementi che contiene la statistica del test V. Nel caso
specifico con un livello di incertezza γ = 5%, e dividendo l’intervallo della sequenza in s = 10 intervalli,
dalle tabelle del χ2 con s-1 = 9 gradi di libertà si ottiene xγ = 16,92. Se ad ogni run della simulazione la
statistica del test è al di sotto di questo valore, le sequenze generata X e Y, possono essere utilizzate per la
simulazione, altrimenti bisogna generare altre sequenza ed annullare la simulazione. Questo modo di
procedere è molto laborioso perché si concentra sull’analisi della singola sequenza di Input. Quando la
sequenza di Input di una simulazione è ottenuta della generazione al calcolatore di numeri pseudo-casuali,
è preferibile analizzare il generatore che si utilizza mediante il test spettrale o altri tipi di test. In questo
modo si concentra l’attenzione sul generatore, ed una volta accertata la bontà del generatore, si possono
56
Esercizi e Complementi
tranquillamente utilizzare tutte le sequenze ottenuto da esso, senza verifiche puntuali che possono essere
molto dispendiose per run di simulazione molto lunghi e con numerosi campioni.
Sulla sequenza di Output che è unica si può condurre il test di Kolmogorov-Smirnov, per verificare se ha
un andamento gaussiano attorno alla media campionaria. In figura viene riportato il test eseguito durante
la simulazione del esercizio 3.1
Test di Kolmogorov-Smirnov
1
0.9
Curva osservata ->
0.8
0.7
F(x)
0.6
0.5
0.4
0.3
<- Curva teorica
0.2
0.1
0
0.75
0.76
0.77
0.78
0.79
0.8
0.81
0.82
x
Il test viene superato anche se la stima ottenuta non è molto buona. Questo significa che il
campione dati ottenuto è gaussiano, e poiché la varianza campionaria che si ottiene vale:
σˆ 2 =
1
N
N
∑(A
i
− Aˆ ) 2 = 1.72 * 10 − 4
i =1
è molto piccola, può darsi che la stima non sia molto precisa a causa del numero esiguo di
campioni utilizzati (M = 100), se ripetiamo l’esercizio 3.1 con M = 10000, e N = 100 si ottiene:
1
Aˆ =
N
π
4
N
∑A
i
= 0.7856
i =1
= 0.7854
Notiamo infine che i valori di M ed N sono il costo della simulazione in termini di impiego delle
risorse del sistema, e di durata della simulazione. La scelta di un buon generatore di sequenze
pseudo-casuali può ridurre notevolmente i costi e la durata della simulazione.
Modelli e Metodi per la Simulazione
Esercizio 3.2
Mediante la simulazione Monte Carlo stimare il valore dei seguenti integrali definiti:
1⎤
⎡
R : ⎢I = ⎥
2⎦
⎣
1
∫
I = xdx
0
⎡ π⎤
R : ⎢I = ⎥
4⎦
⎣
1
I=
dx
1+ x2
0
∫
1/ 2
I=
dx
∫
1− x2
0
1
I=
⎡ π⎤
R : ⎢I = ⎥
6⎦
⎣
R : [I = log 2]
dx
∫1+ x
0
e − 1⎤
⎡
R : ⎢I =
3 ⎥⎦
⎣
1
∫
I = e 3 dx
0
Esercizio 3.3
Mediante la simulazione Monte Carlo stimare il valore della seguente area:
y
1
⎡
π ⎞⎤
⎛
R : ⎢ A = ⎜ π − ⎟⎥
4 ⎠⎦
⎝
⎣
2
x
57
58
Esercizi e Complementi
Esercizio 3.4
Mediante la simulazione Monte Carlo stimare il valore dell’ area racchiusa dalla curva:y2 = x3(2-x)
y
2
R : [A = π ]
x
SIMULAZIONE DI SISTEMI AD EVENTI DISCRETI
MODELLI E SIMULAZIONE
Simulare il comportamento di un sistema significa stimare il valore delle variabili di stato del sistema, e di
altre grandezze che descrivono le prestazioni del sistema. I dati di ingresso di una simulazione sono detti
Input, che possono appartenere a distribuzioni empiriche, teoriche, oppure pseudo-casuali. Sicuramente
questa terza classe di Input è la più utilizzata, perché permette di caratterizzare i fenomeni aleatori al
calcolatore. Le stime dei parametri del sistema vengono ottenute dai dati di uscita della simulazione
denominati Output. Per condurre correttamente una simulazione è molto importante la scelta del modello
che descrive il sistema. Negli esercizi che seguono analizzeremo in dettaglio alcuni modelli elementari
come i sistemi a coda M/M/1, che rappresentano il mattone elementare di molti sistemi complessi. La
grandezza specifica che si analizza di un sistema a coda M/M/1 è il tempo medio di coda in funzione del
carico di lavoro del sistema, ma è possibile anche stimare grandezze diverse come il numero medio di
utenti nel sistema, oppure il coefficiente di utilizzazione del servente. Questo indice in simulazioni più
complesse permette di stimare l’utilizzazione delle risorse durante l’impiego di un sistema. I sistemi a
coda appartengono alla famiglia dei sistemi ad eventi discreti, pertanto viene utilizzata questo tipo di
simulazione per stimarne i parametri. La simulazione ad eventi discreti può essere condotta con due
tecniche differenti: modalità sincrona, comunemente detta time driven simulation, e la modalità asincrona
comunemente detta event driven simulation. La scelta della tecnica appropriata dipende dalle
caratteristiche del sistema, per i sistemi a coda si predilige la simulazione asincrona (event driven).
60
Esercizi e Complementi
Esercizio 4.1
Nella seguente tabella sono riportati i tempi di arrivo e di servizio espressi in minuti di un sistema a coda
M/M/1. Effettuare una simulazione ad eventi discreti (con tempo simulato pari a 20 minuti) del sistema a
coda M/M/1 e stimare il tempo medio di coda, il numero medio di utenti nel sistema, ed il coefficiente di
utilizzazione del servente
Arrivi
1
4
2
1
8
2
4
3
Servizio
2
5
4
1
3
2
1
3
A scopo didattico viene condotta in maniera manuale la simulazione. In ogni caso il lettore può
implementare una simulazione al calcolatore per confrontarla con i risultati ottenuti in questo esercizio. La
prima operazione da compiere è la verifica del modello. Nel testo dell’esercizio viene suggerito di
effettuare una simulazione a eventi discreti di un sistema M/M/1. Affinché il modello sia valido bisogna
verificare che i tempi di inter-arrivo seguano una distribuzione esponenziale, e che i tempi di servizio
seguano una distribuzione esponenziale. In questo particolare esercizio ci viene fornita una sequenza di
dati di ingresso derivata direttamente dall’osservazione di un sistema reale, pertanto siamo in presenza di
una distribuzione empirica di Input. In particolare abbiamo due sequenze di Input XA = tempi di arrivo, XS
= tempi di servizio. Dato il numero esiguo di campioni ( N = 8) si suggerisce di condurre il test di
Kolmogorov-Smirnov (livello di incertezza γ = 5%) per verificare che le due sequenze siano esponenziali.
Senza riportare i dettagli del test più volte illustrati, verifichiamo che per la prima sequenza XA la statistica
del test vale D = 0.1530, dalla tabella non è possibile risalire direttamente al valore di dγ per N = 8, quindi
bisogna procedere per interpolazione, dalla tabella abbiamo in fatti i valori di dγ per N = 5, e N = 10,
quindi sicuramente si avrà : 0.56 ≤ dγ ≤ 0.41, quindi possiamo accettare l’ipotesi che la sequenza di Input
XA segua una distribuzione esponenziale. Analogamente si procede per la sequenza XS ottenendo la
statistica del test pari D = 0.1980. Seguendo le stesse osservazioni fatte in precedenza possiamo accettare
l’ipotesi che la sequenza di Input XS segua una distribuzione esponenziale. A questo punto è possibile
procedere con la simulazione, che viene condotta ad eventi discreti in modalità asincrona (event driven
simulation) pertanto è necessario definire la lista degli eventi, che nel caso specifico è costituita soltanto
da due tipi di eventi: arrivi e partenze. Indichiamo il tempo simulato con TSIM. Questo valore temporale
viene aggiornato ad ogni esecuzione del ciclo principale della simulazione (main control loop). La
simulazione si arresta dopo che si è verificato l’ultimo evento. Per calcolare i parametri del sistema
costruiamo una tabella che riporta per ogni arrivo ed ogni partenza riportata i rispettivi tempi di arrivo di
partenza è di coda:
Modelli e Metodi per la Simulazione
Arrivi
Partenze
1
TAR
TPA
TCODA (D)
1
61
TSIM
1
Il primo evento è sicuramente un arrivo, perché il sistema è vuoto. Il primo utente del sistema viene
accolto subito nel centro di servizio. Per definire il secondo evento bisogna verificare la differenza tra il
tempo di servizio del primo utente (2 min) ed il tempo di arrivo del secondo utente (4 min). Pertanto
l’evento successivo è una partenza:
Arrivi
Partenze
1
TAR
TPA
TCODA (D)
1
1
TSIM
1
2
2
3
A questo punto il tempo simulato vale TSIM = 3 min, e si ripete il ciclo principale della simulazione
aggiornando la lista degli eventi. Poiché il sistema è nuovamente vuoto, il prossimo evento sarà
sicuramente un arrivo:
Arrivi
Partenze
1
TAR
TPA
TCODA (D)
1
1
2
TSIM
1
2
2
5
3
5
Anche questo utente viene subito accolto nel centro di servizio. Dalla sequenza di Input XS si vede che il
tempo di servizio del secondo utente è di 5 min, pertanto uscirà dal sistema quando il tempo simulato sarà
pari a TSIM = 10 min. Chiaramente questa riflessione non è necessaria perché confrontando ad ogni ciclo
tempi di arrivo e tempi di servizio si ottiene lo stesso risultato:
Arrivi
Partenze
1
TAR
TPA
TCODA (D)
1
1
TSIM
1
2
2
3
2
5
5
3
7
7
4
8
8
62
Esercizi e Complementi
Confrontando il tempo di inter-arrivo del 5° utente (8 min) e il tempo di servizio del secondo utente (5
min) si evince che l’evento successivo è una partenza:
Arrivi
Partenze
1
TAR
TPA
TCODA (D)
1
1
TSIM
1
2
2
3
2
5
5
3
7
7
4
8
8
2
10
5
10
TPA
TCODA (D)
TSIM
Il prossimo evento è ancora una partenza:
Arrivi
Partenze
1
TAR
1
1
1
2
2
3
2
5
5
3
7
7
4
8
8
2
10
5
10
3
14
7
14
Il terzo utente è entrato nel sistema quando il tempo simulato aveva valore TSIM = 7 min, ma entra nel
centro di servizio quando esce dal sistema il secondo utente (TSIM = 10 min). Poiché il tempo di servizio
del terzo utente è pari a 4 min, il suo temo complessivo di coda è D = 7 min.
Modelli e Metodi per la Simulazione
A questo punto entra nel centro di servizio il quarto utente, che ha tempo di servizio pari a 1 min:
Arrivi
Partenze
1
TAR
TPA
TCODA (D)
1
1
TSIM
1
2
2
3
2
5
5
3
7
7
4
8
8
2
10
5
10
3
14
7
14
4
15
7
15
TPA
TCODA (D)
TSIM
Il sistema è vuoto, quindi l’evento successivo è un arrivo:
Arrivi
Partenze
1
TAR
1
1
1
2
2
3
2
5
5
3
7
7
4
8
8
5
2
10
5
10
3
14
7
14
4
15
7
15
16
16
63
64
Esercizi e Complementi
Il prossimo evento è ancora un arrivo:
Arrivi
Partenze
1
TAR
TPA
TCODA (D)
1
1
TSIM
1
2
2
3
2
5
5
3
7
7
4
8
8
2
10
5
10
3
14
7
14
4
15
7
15
5
16
16
6
18
18
Seguito da una partenza:
Arrivi
Partenze
1
TAR
TPA
TCODA (D)
1
1
TSIM
1
2
2
3
2
5
5
3
7
7
4
8
8
2
10
5
10
3
14
7
14
4
15
7
15
5
16
16
6
18
18
5
Il prossimo evento è la partenza del sesto utente
19
3
19
Modelli e Metodi per la Simulazione
Arrivi
Partenze
1
TAR
TPA
TCODA (D)
1
1
TSIM
1
2
2
3
2
5
5
3
7
7
4
8
8
2
10
5
10
3
14
7
14
4
15
7
15
5
16
16
6
18
18
5
19
3
19
6
21
3
21
TCODA (D)
TSIM
A questo punto è facile verificare la tabella riepilogativa della simulazione:
Arrivi
Partenze
1
TAR
TPA
1
1
1
2
2
3
2
5
5
3
7
7
4
8
8
2
10
5
10
3
14
7
14
4
15
7
15
5
16
16
6
18
18
5
19
3
19
6
21
3
21
7
22
7
8
22
23
1
26
8
23
26
29
3
29
65
66
Esercizi e Complementi
La sequenza di Output della simulazione è il vettore D = [2, 5, 7, 7, 3, 3, 1, 3]. Poiché viene richiesta
l’analisi per un tempo simulato pari a 20 min la simulazione poteva essere arrestata 1 dopo la partenza del 5
utente ( TSIM = 19 min). Quindi ci limitiamo a stimare il tempo medio di coda sulla sequenza troncata di 5
elementi D* = [2, 5, 7, 7, 3]. Poiché nei sistemi M/M/1 il tempo di coda è una v.a. esponenziale, la stima
del suo valor medio può essere ottenuta mediante la media campionaria:
2+5+7+7+3
Dˆ =
= 4.8
5
Mentre per calcolare il coefficiente di utilizzazione del servente ρ verifichiamo per quanto tempo è stato
impiegato il servente rispetto al tempo totale di osservazione (20 min). Nel grafico riportato di sotto
vengono riportati i due stati in cui può trovarsi il servente (S0 = non attivo, S1 = attivo)
S1
S0
1
2
3
4
5
6
7
8
9
10 11 12 13 14 15 16 17 18 19 20 t
Dall’area tratteggiata si risale al tempo totale di attività del servente 2 (16 min), pertanto il valore stimato di
ρ è:
ρˆ =
1
16
= 0.8
20
Molto spesso queste simulazioni vengono condotte definendo un tempo limite (Tmax) per il tempo simulato. Questo
significa aggiungere un controllo all’inizio del ciclo principale della simulazione (main control loop). Se il tempo
simulato è inferiore a Tmax la simulazione procede, altrimenti si arresta.
2
Questo valore nei sistemi M/M/1 corrisponde anche al Throughput.
Modelli e Metodi per la Simulazione
67
Allo stesso modo si procede per il numero di utenti nel sistema:
n(t)
3
2
1
0
1
2
3
4
5
6
7
8
9
10 11 12 13 14 15 16 17 18 19 20 t
Dall’area tratteggiata si risale al numero medio di utenti nel sistema:
20
nˆ =
1
26
n(t )dt =
= 1 .3
20 0
20
∫
Tutti questi risultati sono delle stime dei parametri del sistema, perché ottenuti mediante una simulazione.
Dalla tabella riepilogativa della simulazione, è possibile verificare come il tempo simulato abbia degli
incrementi irregolare, da questa osservazione discende il nome che si dà a questo tipo di simulazione ad
eventi discreti, cioè asincrona.
68
Esercizi e Complementi
Complemento 4.1
Un’ importante risultato della teoria delle code è il teorema di Burke, che descrive il processo di uscita di
un sistema a coda M/M/1, come un processo di Poisson della stessa intensità λ del processo di arrivo.
Questo significa che un’ utile verifica del corretto funzionamento della simulazione, è la verifica che i
tempi di inter-partenza seguano una distribuzione esponenziale con valor medio pari a 1/λ. Un altro
risultato importante della teoria delle code è che il tempo di coda è una v.a. esponenziale negativa con
valor medio pari a:
E[D] =
1
(μ − λ )
Complemento 4.2
Quando viene effettuata una simulazione vengono effettuate due operazioni molto importati
prima di accettare il risultato: la verifica della simulazione, e la validazione della simulazione. La
verifica della simulazione consiste nel accertare che il modello della simulazione funzioni nel
modo appropriato, secondo quelli che sono gli intendimenti di chi realizza la simulazione. Ad
esempio nel caso specifico dell’esercizio 4.1. la verifica consiste nel accertamento che il modello
della simulazione si comporti realmente con un sistema M/M/1. La validazione della simulazione
consiste nel confermare che il modello della simulazione si comporti nella maniera più simile al
sistema reale oggetto di studio. La validazione può essere condotta in maniera qualitativa, per
sistemi che non hanno un elevato grado di complessità, mentre per sistemi molto complessi
possono essere necessarie delle verifiche sperimentali, che si ottengono sollecitando il sistema ed
il modello della simulazione con gli stessi input e verificando che hanno la stessa risposta agli
input e producono lo stesso risultato. Questo tipo di validazione è anche chiamata verifica
sperimentale della simulazione ed è un procedimento molto costoso ma alle volte necessario.
Modelli e Metodi per la Simulazione
69
Esercizio 4.2
Effettuare una simulazione ad eventi discreti di un sistema a coda M/M/1, con frequenza media de
processo di arrivo pari a λ = 4 arrivi al minuto, frequenza media di servizio pari a μ = 5 partenze al
minuto.Calcolare il tempo medio di coda, ed il coefficiente di utilizzazione dei serventi, dopo un’ora di
osservazione.
Ripetere la simulazione con tempo di servizio deterministico con valore pariμ = 5 partenze al minuto, e
confrontare i risultati ottenuti.
Complemento 4.3
La simulazione negli ultimi anni ha avuto un forte impulso, grazie alle sue enorme potenzialità possiamo
riassumere i vantaggi dell’utilizzo della simulazione rispetto alla progettazione tradizionale nei seguenti
punti:
‰ E’ possibile analizzare sistemi complessi, la cui rappresentazione analitica è impraticabile;
‰ E’ possibile ripetere a costo nullo, molte volte l’esperimento, e sollecitare il sistema con una
gamma molto ampia di Input, non realizzabili in esperimenti reali;
‰ Permette di capire a fondo le relazioni tra le variabili di stato,e gli indici di prestazione di un
sistema, mediante la registrazione della simulazione ed un’analisi dettagliata di tutte le iterazioni tra
le varie parti del modello.
Altresì è importante ricordare alcuni aspetti negativi:
‰ Il risultato di una simulazione è una stima del comportamento del sistema, quindi la simulazione
non produce risultati esatti;
‰ E’ necessario utilizzare strumenti statistici per verificare e validare una simulazione, prima di
accettare un risultato;
‰ Per implementare una simulazione è necessario individuare un modello del sistema reale oggetto
di studio. La scelta di un modello significa molto spesso effettuare delle semplificazioni, per poter
riprodurre al calcolatore determinati esperimenti. Questo significa che spesso le simulazioni
forniscono solo un indicazione del comportamento del sistema, e quindi bisogna fare attenzione
all’utilizzo dei risultati.
In definitiva la simulazione, nel campo della progettazione, o in altri campi può essere uno strumento
molto valido se utilizzato nella maniera appropriata.