Document

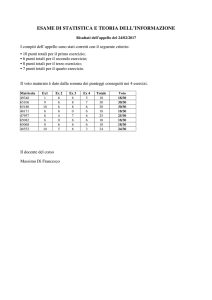
Probabilità Condizionata
• Definizione
– Dato uno spazio di probabilità (S, A, P[.]) si
definisce probabilità condizionata dell’evento E
dato l’evento F, con E ed F eventi qualunque di A,
il rapporto:
PEF 
PE F  
PF 
con PF   0
Esempio
Consideriamo il lancio di una coppia di dadi
– Sia l’evento E=“la somma dei numeri dei due dadi
non sia superiore a 8”
– Sia l’evento F=“compaia almeno un 5”
1
2
3
4
5
6
1
2
3
4
5
6
7
2
3
4
5
6
7
8
3
4
5
6
7
8
9
4
5
6
7
8
9
10
5
6
7
8
9
10
11
6
7
8
9
10
11
12
Risultato del dado
evento E
evento F
26
PE  
36
11
PF  
36
Esempio
Se si volesse calcolare quale sia la probabilità
dell’evento E=“la somma dei numeri dei due dadi
non sia superiore a 8” condizionato all’evento
F=“compaia almeno un 5”, allora
1
2
3
4
5
6
6
1
2
3
4
5
6
7
PE F  
2
3
4
5
6
7
8
3
4
5
6
7
8
9
11
4
5
6
5
6
7
6
7
8
7
8
9
8
9
10
9
10
11
Risultato del dado
evento E
evento F
10
11
12
6
PEF  36 6
PE F  


PF  11 11
36
Formula delle probabilità totali
• Esempio
Una ditta produttrice di autovetture riceve da quattro fornitori
le pastiglie dei freni da installare sulle auto prodotte nelle
seguenti percentuali: 65%, 20%, 10%, 5%.
Sapendo che i quattro fornitori producono le pastiglie con una
difettosità rispettivamente del 2%, 2.5%, 4%, 10%,
si vuole sapere la probabilità che ha la ditta produttrice di
automobili di ricevere un componente difettoso.
S
B1
B4
A
B3
B2
Evidentemente si ha che:
con Bi  B j   i  j
B1  B2  B3  B4  S
e quindi:
A  AB1  B2  B3  B4   AB1  AB2  AB3  AB4
da cui, sfruttando il terzo assioma di Kolmogoroff si ha:
4
P A   P ABi 
i 1
S
B1
B4
A
B3
B2
Ricordando la definizione di probabilità condizionata:
P ABi 
PA Bi  
PBi 
 P ABi   PA Bi  PBi 
e quindi sostituendo si ha:
P A   PA Bi  PBi 
4
i 1
Questa relazione prende il nome di
FORMULA DELLE PROBABILITÀ TOTALI
Formula delle probabilità totali
• Teorema
Sia E1, E2, .. En una collezione di eventi incompatibili tali per
cui
n
S   Ei
i 1
e
PEi   0 i
cioè eventi esaustivi, qualsiasi sia F (sottoinsieme di S) si ha:
PF    PF Ei  PEi 
n
i 1
Formula delle probabilità totali
rappresentazione ad albero
PF    PF Ei  PEi 
n
i 1
PF E1 
PE1 
PE2 
PF E2 
F
F
F
PEn 
PF En 
F
F
Tornando all’esempio presentato si ha:
PB1  PA B1   0.65  0.02
PB2  PA B2   0.20  0.025
PB3  PA B3   0.10  0.04
PB4  PA B4   0.05  0.10
e quindi:
P A  0.027
 2.7%
Formula di Bayes
• Esempio (continuazione)
A questo punto potrebbe essere interessante chiedersi quale
sia la probabilità che, una volta selezionata una pastiglia fra
tutte quelle difettose, questa provenga dal secondo fornitore.
PB2 A PA B2  PB2 
PB2 A 
 n
P A
 PA Bi  PBi 
i 1
S
B1
B4
A
B3
B2
Tornando all’esempio presentato si ha:
PB2  PA B2   0.20  0.025
PA  0.027
e quindi:
PA B2  PB2 
PB2 A
0.005
PB2 A 
 n

 0.1852
PA
0.027
 PA Bi  PBi 
i 1
PB2 A  18.52%
Analogamente per gli altri fornitori si ha:
PB1 A 0.65  0.02
PB1 A 

 0.4815
PA
0.027
PB3 A 0.10  0.04
PB3 A 

 0.1481
PA
0.027
PB4 A 0.05  0.10
PB4 A 

 0.1852
PA
0.027
Formula di Bayes
• Teorema
Sia E1, E2, .. En una collezione di eventi incompatibili ed
esaustivi, cioè
Ei  E j   i  j
n
S   Ei
i 1
e
qualsiasi sia F (sottoinsieme di S) si ha:
PEk F  
PF Ek  PEk 
 PF Ei  PEi 
n
i 1
PEi   0 i
Indipendenza stocastica
• Definizione
Due eventi E ed F appartenenti allo stesso spazio degli eventi
si dicono indipendenti (o stocasticamente indipendenti) se e
soltanto se una delle seguenti condizioni è soddisfatta:
PEF   PE  PF 
PE F   PE 
PF E   PF 
se PF   0
se PE   0
La proprietà di indipendenza stocastica e di incompatibilità
sono due proprietà distinte da non confondere