2009-10 Prof. G. Galeotti – Materiali
5.
Equilibrio del consumatore e domanda dei beni
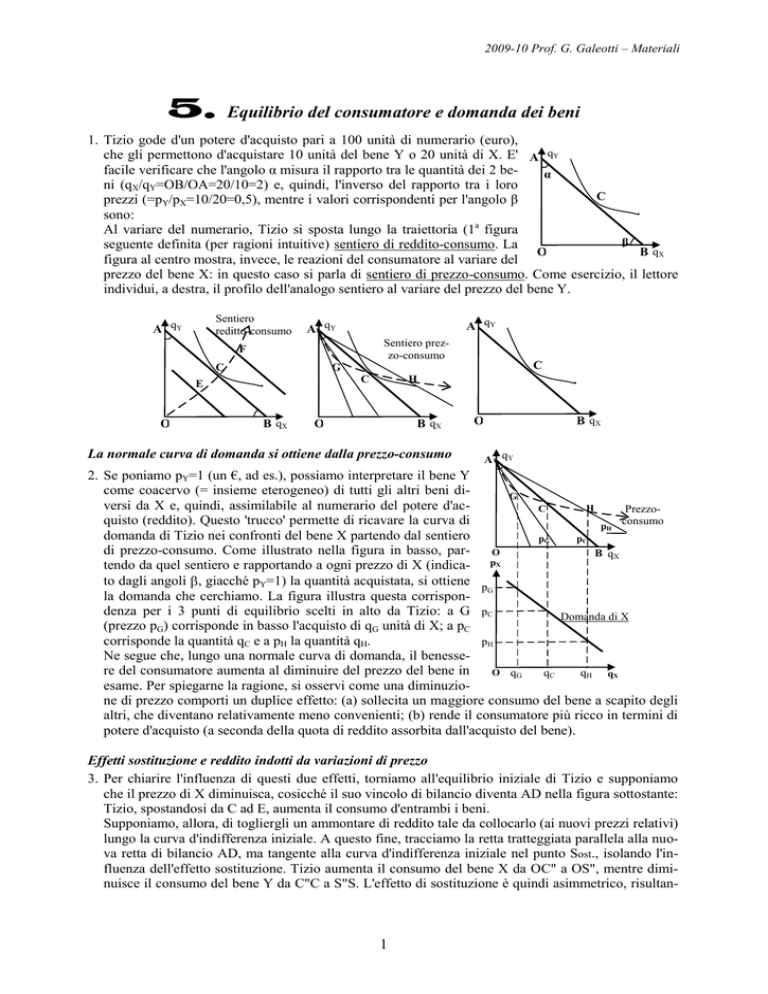
1. Tizio gode d'un potere d'acquisto pari a 100 unità di numerario (euro),
che gli permettono d'acquistare 10 unità del bene Y o 20 unità di X. E' A qY
facile verificare che l'angolo α misura il rapporto tra le quantità dei 2 beα
ni (qX/qY=OB/OA=20/10=2) e, quindi, l'inverso del rapporto tra i loro
C
prezzi (=pY/pX=10/20=0,5), mentre i valori corrispondenti per l'angolo β
sono:
Al variare del numerario, Tizio si sposta lungo la traiettoria (1a figura
β
seguente definita (per ragioni intuitive) sentiero di reddito-consumo. La
O
B qX
figura al centro mostra, invece, le reazioni del consumatore al variare del
prezzo del bene X: in questo caso si parla di sentiero di prezzo-consumo. Come esercizio, il lettore
individui, a destra, il profilo dell'analogo sentiero al variare del prezzo del bene Y.
Sentiero
reditto-consumo
A qY
A qY
A qY
Sentiero prezzo-consumo
F
H
C
E
O
C
G
C
B qX
O
B qX
La normale curva di domanda si ottiene dalla prezzo-consumo
O
B qX
A qY
2. Se poniamo pY=1 (un €, ad es.), possiamo interpretare il bene Y
come coacervo (= insieme eterogeneo) di tutti gli altri beni diG
versi da X e, quindi, assimilabile al numerario del potere d'acH
C
Prezzoquisto (reddito). Questo 'trucco' permette di ricavare la curva di
consumo
pH
domanda di Tizio nei confronti del bene X partendo dal sentiero
pG
pC
di prezzo-consumo. Come illustrato nella figura in basso, parO
B qX
tendo da quel sentiero e rapportando a ogni prezzo di X (indica- pX
to dagli angoli , giacché pY=1) la quantità acquistata, si ottiene p
G
la domanda che cerchiamo. La figura illustra questa corrispondenza per i 3 punti di equilibrio scelti in alto da Tizio: a G pC
Domanda di X
(prezzo pG) corrisponde in basso l'acquisto di qG unità di X; a pC
corrisponde la quantità qC e a pH la quantità qH.
pH
Ne segue che, lungo una normale curva di domanda, il benessere del consumatore aumenta al diminuire del prezzo del bene in
O qG
qC
qH qX
esame. Per spiegarne la ragione, si osservi come una diminuzione di prezzo comporti un duplice effetto: (a) sollecita un maggiore consumo del bene a scapito degli
altri, che diventano relativamente meno convenienti; (b) rende il consumatore più ricco in termini di
potere d'acquisto (a seconda della quota di reddito assorbita dall'acquisto del bene).
Effetti sostituzione e reddito indotti da variazioni di prezzo
3. Per chiarire l'influenza di questi due effetti, torniamo all'equilibrio iniziale di Tizio e supponiamo
che il prezzo di X diminuisca, cosicché il suo vincolo di bilancio diventa AD nella figura sottostante:
Tizio, spostandosi da C ad E, aumenta il consumo d'entrambi i beni.
Supponiamo, allora, di togliergli un ammontare di reddito tale da collocarlo (ai nuovi prezzi relativi)
lungo la curva d'indifferenza iniziale. A questo fine, tracciamo la retta tratteggiata parallela alla nuova retta di bilancio AD, ma tangente alla curva d'indifferenza iniziale nel punto Sost., isolando l'influenza dell'effetto sostituzione. Tizio aumenta il consumo del bene X da OC" a OS", mentre diminuisce il consumo del bene Y da C"C a S"S. L'effetto di sostituzione è quindi asimmetrico, risultan-
1
2009-10 Prof. G. Galeotti – Materiali
qY
do favorevole al bene X (il cui prezzo è diminuito), e conA
trario al consumo del bene Y, il cui prezzo relativo è aumentato.
Quanto all'effetto reddito (passaggio da S ad E), la sua influenza è simmetrica, giacché è favorevole al consumo di
A'
E
entrambi i beni: il consumo di X aumenta ulteriormente (per E'
C
C'
l'ammontare S"E"), mentre il consumo di Y aumenta di un
ammontare che (in questo caso) più che compensa l'influenSost.
za negativa dell'effetto sostituzione, aumentandone il con- S'
sumo da C"C a E"E: se l'effetto reddito fosse inferiore all'efD
D'
qX
fetto di sostituzione, Y sarebbe un bene 'inferiore' (se ne
C" S" E"
1
consuma meno quando si è più 'ricchi') .
SE DIMINUISCE IL PREZZO RELATIVO DI X:
Importante: l'effetto reddito della variazione di prezzo di un
il passaggio da C a S mostra l'effetto di
bene è significativo solo quando quel bene assorbe una quosostituzione, favorevole a X (+C"S") e
ta rilevante del potere di acquisto del consumatore2.
contrario al bene Y (-C'S');
il passaggio da S a E mostra che l'effetto reddito è favorevole al consumo
d'entrambi i beni, se non si tratta di beni inferiori.
Quindi, il passaggio da C ad E esprime
l'effetto totale della variazione di prezzo.
Un esempio d'effetto reddito rilevante: la scelta tra consumo
oggi e consumo domani (=risparmio oggi)
4. Consideriamo un modello a due periodi – oggi e domani
(tra un anno, ad es.) – definendo risparmio quanto non è
consumato oggi. La scelta sul come distribuire i consumi tra oggi e domani dipende dalle preferenze
intertemporali individuali, che possono variare dal preoccuparsi solo dell'oggi (cicala) al preoccuparsi soprattutto del domani (formica). Se misuriamo il consumo attuale lungo l'asse orizzontale e quello
di domani lungo l'asse verticale, le curve d'indifferenza della cicala – caratterizzata da una totale
miopia intertemporale – si presenterebbero come rette verticali, mentre quelle della formica come
rette orizzontali (la sua ipermetropia temporale la porta ad apprezzare solo il consumo futuro). Se
supponiamo ragionevolmente che consumo attuale e consumo futuro presentino rendimenti marginali
decrescenti, avremo le normali curve di indifferenza dal profilo concavo.
Consumo domani
Tasso di rendimento nullo: il soggetto
risparmia EA, assicurandosi domani
un consumo OD.
E
L
Se il tasso di rendimento è positivo,
il risparmio aumenta se l'effetto sostituzione è maggiore
dell'effetto reddito.
A
H
Eliminando l'effetto reddito,
l'effetto di sostituzione è favorevole al risparmio
H'
L'
C
C
45°=1
O
H
B
B
D
Consumo domani
Consumo domani
_L
C
2
ConsuConsumo
45°
2
! F
mo oggi
oggi
O S
A
E
A
E
Il risparmio (FA) diminuisce
SE = aumento del risparmio doperché l'effetto sostituzione (pro
vuto all'effetto di sostituzione
risparmio) è minore dell'effetto
reddito (contrario al risparmio)
Consumo
oggi
O
EA= risparmio= non
consumo oggi
Quanto alla retta di bilancio, se poniamo che il potere d'acquisto di 'oggi' sia pari a OA, il potere
d'acquisto di 'domani' dipende (a) da quanto si risparmia oggi e (b) da quanto renderà domani il risparmio d'oggi. La 1a figura mostra il caso in cui questo rendimento sia nullo: se il risparmio è conservato sotto il materasso, la retta di bilancio presenta un'inclinazione di 45°, vale a dire il reddito disponibile domani è pari al risparmio d'oggi (OB=OA). La figura centrale presenta, invece, il caso di
un rendimento del 100%: se oggi non si consuma, domani si disporrà di OH pari al doppio di OA.
1
2
Se, partendo da E, si suppone che il prezzo di X aumenti, l'influenza di entrambi gli effetti è in direzione opposta.
In questo senso, le nostre consuete presentazioni grafiche a 2 beni tendono a sovrastimare l'influenza dell'effetto reddito.
2
2009-10 Prof. G. Galeotti – Materiali
5. L'equilibrio della prima ipotesi mostra un consumo attuale pari ad OE ed un consumo futuro pari ad
OD. Il costo opportunità di quel consumo futuro è dato da EA1. Ci chiediamo: quando aumenta il
rendimento del capitale risparmiato, Tizio risparmierà di più o di meno? Per rispondere, passiamo alla figura centrale e consideriamo il nuovo equilibrio L, lungo la nuova retta di bilancio HA: il risparmio diminuisce, risultando pari ad FA, come spiegano le didascalie dell'ultima figura.
La curva di domanda compensata (a benessere
Y
costante)
Curva d'indifferenza tra i
6. Nel nostro studio è preferibile considerare
beni Y(=R) e X.
funzioni di domanda che non includano l'effetSe pR=1, R si presenta coto reddito, ma tengano solo conto dell'effetto
TSA=10
me numerario (= reddito o
A
L
di sostituzione: si parla di domanda compenpotere d'acquisto)
sata proprio perché compensata da variazioni
B
TSB=7
di reddito di segno opposto che lasciano il benessere del consumatore immutato. In concreC
TSC=2
N
to, si tratta solo di ricavare la domanda dalla
curva d'indifferenza sulla quale è inizialmente
collocato il consumatore. In questo modo, i
suoi prezzi di domanda esprimono la disponiO
X
XA
XC
bilità marginale a spendere per il bene (o servizio), cosicché l'area sottesa alla domanda
La distanza LN in alA'
to esprime lo stesso
pA=10
esprime la sua disponibilità totale a spendere
valore (ammontare di
(con pY=1, il bene Y esprime sempre il potere
euro) dell'area del
B'
pB=7
d'acquisto di Tizio).
trapezio ombreggiato
XAA'C'XC
7. Lungo la curva d'indifferenza in alto, se Tizio
C'
è collocato in A (con coordinate OL e OXA), il
pC=2
suo tasso di sostituzione (- Y/ X)A è eguale
all'inverso dei prezzi pX/pY e (con pY=1) abO
X
XC
XA
XB
biamo (- Y/ X)A=pX= 10 €. Riportiamo questi 10 € lungo l'asse verticale in basso, come
coordinata del punto A': la quantità OXA è identica nelle due figure. In A', quindi, pX esprime la sua
disponibilità marginale a spendere (=rinuncia marginale a Y) per un incremento di X. Replicando
quest'operazione per tutti i punti successivi della curva d'indifferenza (esemplificati in B e in C, cui
corrispondono i punti B' e C'), otteniamo la disponibilità marginale a spendere di Tizio per incrementi successivi di X. Non dovrebbe essere difficile intuire, allora, che il valore numerico di LN è
eguale, nella figura in basso, all'area del trapezio (ombreggiato) sotteso alla curva di domanda nel
tratto da A' a C'. Quest'area, infatti, equivale alla somma di tutte quelle rinunce marginali ad Y, qui
direttamente espresse come prezzi. Ponendo XA=5 e XC=15, il lettore calcoli l'area del trapezio e
rifichi se la disponibilità totale a spendere di Tizio sia o meno eguale a 60 € (=LN = XAA'C'Xc).
8. Possiamo seguire un ragionamento analogo per ricavare la curva di offerta compensata dell'impegno
che Caio (artigiano o professionista) mette nella prestazione da eseguire. In questo caso, i prezzi
d'offerta esprimono disponibilità marginali ad impegnarsi con accuratezza crescente, in cambio di
una remunerazione crescente.
Consideriamo una curva d'indifferenza di Caio, misurando in verticale il bene Y, come già definito
(pY=1), e in orizzontale il livello d'impegno, che gli comporta un costo crescente2.
Movendosi lungo la curva, nel punto 1 il suo tasso di sostituzione tra incremento di R e incremento
d'impegno è pari a 20 €, mentre nel punto 2, il maggiore impegno marginale compensato da 70 €.
1
Anche un raddoppio del reddito di oggi comporta una riduzione di risparmio.
Trattandosi di un costo (un 'male') le curve d'indifferenza presentano un profilo concavo verso sinistra, in quanto il costo di
un maggiore livello d'accuratezza dovrà essere compensato da ammontari di Y crescenti più che proporzionalmente al livello
d'impegno: nei dintorni dell'origine (impegno pressoché nullo) il tasso di sostituzione è prossimo a zero.
2
3
2009-10 Prof. G. Galeotti – Materiali
Curva d'indifferenza tra il
bene R e impegno adempimento. Se pR=1, R si presenta come numerario del
potere d'acquisto.
Y
Riportando queste valutazioni marginali lungo l'asse verticale in basso, in corrispondenza dei livelli
crescenti d'impegno, siamo in grado d'identificare
2
E
la sua curva d'offerta compensata.
La distanza OE esprime
TS2=70
lo stesso valore (euro)
9. Anche in questo caso, il passaggio da 0 a 1 prima,
dell'area del triangolo
e da 1 a 2 poi, è scomposto in tante variazioni
OFA2 in basso
marginali successive, cosicché OE (in alto) esprime il totale degli incrementi marginali di Y neces1
D
sari a lasciare immutato il benessere di Caio
all'aumentare del suo impegno. Come nel caso delTS1=20
la domanda, l'ammontare OE di R è eguale all'area
Impegno neldel triangolo sotteso (siamo partiti dall'origine),
A2
O
A1
l'adempimento
nella figura in basso, alla curva d'offerta OF.
Ponendo OA2=100 (senza indagare sull'unità di
p2=70
misura!), il lettore calcoli la remunerazione totale
F
(l'area del triangolo OFA2) richiesta per quel livello d'impegno.
p1=20
10. Il vantaggio di questa presentazione in termini di
aree sottese alla curve di domanda e offerta è nel
mostrare il 'valore sociale' della divisione sociale
Impegno nelO
del lavoro e l'efficienza paretiana perseguita impliA1
A2 l'Adempimento
citamente dalla normativa civilistica di default che
incoraggia la rivelazione delle preferenze dei contraenti, dalle quali dipende la creazione di valore
assicurata dal contratto. E' sufficiente, infatti, notare come un impegno minore (OXm, nella figura a
destra) comporterebbe per il committente una perdita di benessere maggiore dei costi risparmiati
dall'agente (trapezio XmCEXE); il viceversa avviene per un impegno maggiore (per OXM, gli ulteriori
costi totali del costruttore sono maggiori che benessere che forniscono a Etro). I triangoli quadrettati
indicano le perdite secche di benessere sociale di questi equilibri inefficienti.
11. Secondo il criterio di Pareto, il passaggio da un equilibrio (come Xm o XM) ad un altro (es., XE) è efficiente quando migliora il benessere di almeno un soggetto, senza detrimento del benessere di altri.
Attenzione: quando nel passaggio il miglioramento di qualcuno accompagnato dal peggioramento di
almeno un altro soggetto, i due equilibri sono inconfrontabili, non esistendo parametri oggettivi per
confrontare il benessere di soggetti diversi. Non si può, tuttavia, affermare che un equilibrio efficiente è sempre preferibile a un equilibrio inefficiente (come suggerirebbe la grammatica!), se prima non
si accerta che i due equilibri siano confrontabili. Nel caso in esame, lo sono per una ragione immediata: nel passaggio da Xm a XE il committente è disposto a rimborsare i maggiori costi dell'agente,
migliorando il proprio benessere (viceversa, nel passaggio da XM a XE).
Disponibilità
marginali
A
OAE = valore netto massimo creato
dall'adempimento
concordato OXE
Disponibilità
marginali
Perdite secche di valore (=benessere) per
A
difetto (CDE) o per
Domanda
eccesso (EFG)
d'impegno
Offerta
dell'agente
F
C
E
E
D
Domanda del
committente
G
Offerta
impegno
B
O
XE
X=impegno nell'adempiere O
4
Xm
XE
XM












