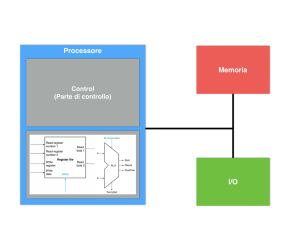
Calcolatori Elettronici
Nell’unità di calcolo
L’unità aritmetico-logica (ALU)
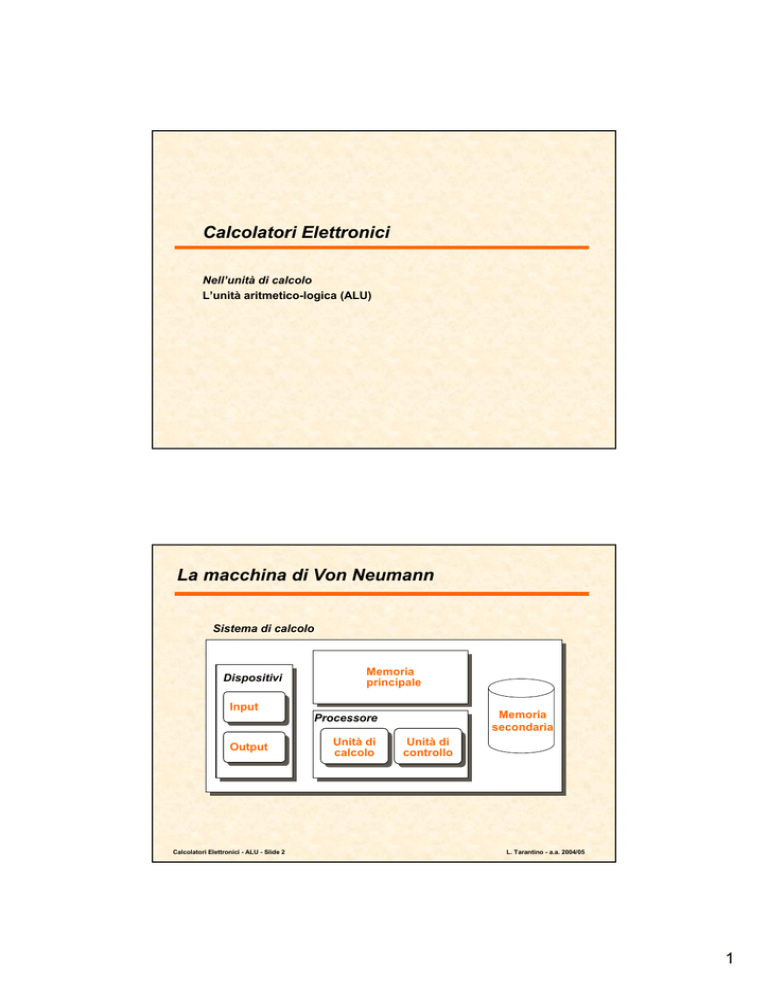
La macchina di Von Neumann
Sistema di calcolo
Dispositivi
Memoria
principale
Input
Memoria
secondaria
Processore
Output
Calcolatori Elettronici - ALU - Slide 2
Unità di
calcolo
Unità di
controllo
L. Tarantino - a.a. 2004/05
1
L’unità di calcolo
Processore
Unità di
controllo
Unità di
calcolo
Unità di calcolo
Elementi di
memoria
(registri)
Elementi di
calcolo
Calcolatori Elettronici - ALU - Slide 3
L. Tarantino - a.a. 2004/05
Elementi di calcolo
Operazioni aritmetiche
addizione/sottrazione
moltiplicazione/divisione
AND
OR
NOT
Operazioni logiche
necessaria per determinare
il complemento a 2
Unità aritmetico-logica
Arithmetic - Logic Unit
ALU
Calcolatori Elettronici - ALU - Slide 4
L. Tarantino - a.a. 2004/05
2
ALU - il progetto
operandi da 32 bit
costruisco una ALU per operandi da 1 bit
integro opportunamente 32 ALU da 1 bit per ottenere una ALU da 32
bit
Operazione
a
ALU a 1 bit
b
Risultato
1 bit
Calcolatori Elettronici - ALU - Slide 5
L. Tarantino - a.a. 2004/05
Elementi costitutivi di base
Porta AND
a
b
a
b
Porta NOT
c
a
0
0
1
1
b
0
1
0
1
c
0
0
0
1
Porta OR
a
C
d
Calcolatori Elettronici - ALU - Slide 6
a
0
0
1
1
b
0
1
0
1
c
0
1
1
1
c
1
0
d
0
1
c
a
b
Multiplexer
c
a
0
1
a
0
b
1
C
L. Tarantino - a.a. 2004/05
3
ALU a 1 bit - prima versione (1)
inseriamo AND, OR, somma aritmetica
Operazione
Risultato = a AND b
oppure
Risultato = a OR b
Multiplexer
oppure
Risultato = a + b
a AND b
0
a OR b
1
a + b
2
Risultato
ci serve un sommatore
Calcolatori Elettronici - ALU - Slide 7
L. Tarantino - a.a. 2004/05
Il sommatore (a 1 bit)
Contesto
somma di operandi da 32 bit
rn-1 rn-2
r1 r0
xn-1 xn-2 … x1 x0 +
yn-1 yn-2 … y1 y0 =
sn sn-1 sn-2 … s1 s0
devo considerare il riporto
proveniente dalla coppia
di bit precedente
riporto “interno”
CarryIn
a
+
somma
b
CarryOut
riporto “esterno”
Calcolatori Elettronici - ALU - Slide 8
L. Tarantino - a.a. 2004/05
4
ALU a 1 bit - prima versione (2)
Op
CarryIn
Op
a
a AND b
0
a OR b
1
a + b
2
0
1
Ris
+
b
Ris
2
ALU a 1 bit
CarryOut
Calcolatori Elettronici - ALU - Slide 9
L. Tarantino - a.a. 2004/05
ALU a 32 bit
CarryIn0 = 0
A ≡ an-1 an-2 … a1 a0
Operazione
CarryIn
a0
B ≡ bn-1 bn-2 … b1 b0
ALU0
bo
B
A
Ris0
CarryOut
CarryIn
a1
ALU1
b1
ALU a n bit
Ris1
CarryOut
Op
CarryIn
a31
ALU3\
Ris
Calcolatori Elettronici - ALU - Slide 10
b31
Ris31
CarryOut
L. Tarantino - a.a. 2004/05
5
ALU a 1 bit - seconda versione (1)
inseriamo la sottrazione: a - b = a + (-b)
a-b=a+b+1
-b=b+1
Osservazione
se mando a e b in ingresso al sommatore e pongo CarryIn = 1
ottengo in uscita a + b + 1
CarryIn = 1
a
a + b + 1
+
b
CarryOut
Calcolatori Elettronici - ALU - Slide 11
L. Tarantino - a.a. 2004/05
ALU a 1 bit - seconda versione (2)
Op
Inverti
CarryIn
a
0
1
b
Ris
0
+
2
1
CarryOut
Calcolatori Elettronici - ALU - Slide 12
L. Tarantino - a.a. 2004/05
6
ALU a 32 bit
stesso schema
quando devo fare una sottrazione pongo CarryIn0 = 1
CarryIn0
rn-1 rn-2
r1 r0 r-1
xn-1 xn-2 … x1 x0 +
yn-1 yn-2 … y1 y0 =
sn sn-1 sn-2 … s1 s0
la linea inverti è una qualche elaborazione della linea Operazione
Calcolatori Elettronici - ALU - Slide 13
L. Tarantino - a.a. 2004/05
Gestione dell’overflow
overflow = f (an-1 , bn-1, sn-1 )
Op
Inverti
CarryIn
a
0
1
b
Ris
0
+
2
1
CarryOut
Overflow
detection
Calcolatori Elettronici - ALU - Slide 14
Overflow
L. Tarantino - a.a. 2004/05
7