Ottica Geometrica
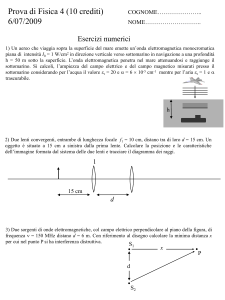
Diottro
Sistema Ottico con sup.
sferica tra due dielettrici
Rifrazione in ap.pa.
raggi omocentrici
Equazione del diottro o dei punti coniugati o
formula di Gauss per una superficie sferica
Ottica Astronomica AA1617
Ottica Geometrica
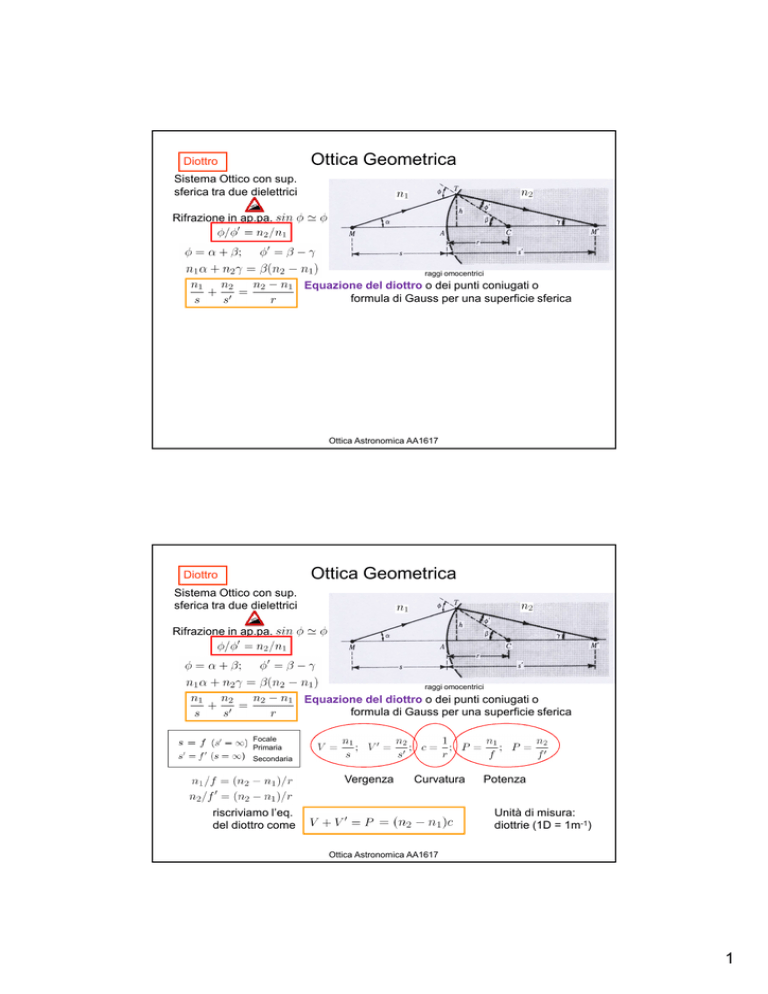
Diottro
Sistema Ottico con sup.
sferica tra due dielettrici
Rifrazione in ap.pa.
raggi omocentrici
Equazione del diottro o dei punti coniugati o
formula di Gauss per una superficie sferica
Focale
Primaria
Secondaria
Vergenza
Curvatura
riscriviamo l’eq.
del diottro come
Potenza
Unità di misura:
diottrie (1D = 1m-1)
Ottica Astronomica AA1617
1
Ottica Geometrica
Diottro
Convesso
Convergente
Concavo
Divergente
C a DX di V
C a SX di V
Fuochi
primari
Fuochi
secondari
centro di curvatura
fuoco
vertice
Ottica Astronomica AA1617
Diottro
Ottica Geometrica
Magnificazione Laterale o Trasversa
Magnificazione Angolare
dalla quale si ricava che
Invariante di Lagrange o di Helmoltz o, semplicemente, Invariante Ottico
Valido sempre in sistemi privi di aberrazioni e
ricorda la Condizione di Abbe del seno
Quadrando e moltiplicando per
la conservazione del throughput
otteniamo
Ottica Astronomica AA1617
2
Specchio
sferico
Ottica Geometrica
Riflessione in ap.pa.
riscriviamo l’eq. del diottro con
Ottica Astronomica AA1617
Lente sottile (caso ideale):
Ottica Geometrica
Sistema Ottico Centrato
composto da 2 diottri
separati da distanza trascurabile rispetto alle
altre distanze in gioco
dalla reversibilità…
nel caso di lente (n1) nello stesso n2 abbiamo
Formula della lente in (*)
forma gaussiana
forma newtoniana
(*) ricavate da similitudini tra triangoli
Ray tracing: metodo dei raggi
Ottica Astronomica AA1617
paralleli o dei fuochi
3
Lente sottile (caso ideale):
Ottica Geometrica
Sistema Ottico Centrato
composto da 2 diottri
separati da distanza trascurabile rispetto alle
altre distanze in gioco
dalla reversibilità…
nel caso di lente (n1) nello stesso n2 abbiamo
Formula della lente in (*)
forma gaussiana
forma newtoniana
Formula del “fabbricante di lenti”
(*) ricavate da similitudini tra triangoli
Ray tracing: metodo dei raggi
Ottica Astronomica AA1617
paralleli o dei fuochi
Lente sottile (caso ideale)
Ottica Geometrica
Lente divergente
∀s
f<0 e f’<0
F’
Immagine
virtuale, dritta e
rimpicciolita
F
s
biconcava
Ottica Astronomica AA1617
4
Lente sottile (caso ideale)
Ottica Geometrica
Lente divergente
∀s
f<0 e f’<0
F’
Immagine
virtuale, dritta e
rimpicciolita
F
s
biconcava
Lente convergente
s>2f
f>0 e f’>0
s=2f
F
F’
f<s<2f
s
biconvessa
0<s<f
Ottica Astronomica AA1617
Immagine reale,
capovolta e
rimpicciolita
Immagine reale,
capovolta e
uguale
Immagine reale,
capovolta e
ingrandita
Immagine
virtuale, dritta e
ingrandita
Ottica Geometrica
2 Lenti sottili
L1
L2
F1
F’1
s
F2
d
F’2
s'
1) relazioni ogg-imm delle 2 lenti sottili + 2) ogg = ∞ e poi imm = ∞
Posizione Fuoco secondario
(distanza da V di L2)
,
Posizione Fuoco primario
(distanza da V di L1)
Ottica Astronomica AA1617
5
Ottica Geometrica
2 Lenti sottili
L1
L2
F1
F’1
s
F2
d
F’2
s'
1) relazioni ogg-imm delle 2 lenti sottili + 2) ogg = ∞ e poi imm = ∞
Posizione Fuoco secondario
(distanza da V di L2)
Caso: 2 lenti incollate (d=0)
,
Posizione Fuoco primario
(distanza da V di L1)
Ottica Astronomica AA1617
6