SISTEMA SEMPLICE
Il sistema semplice è costituito da una sostanza pura il cui stato intensivo sia
individuato da due proprietà interne intensive indipendenti.
Il sistema semplice comprimibile o sistema p,v,T è detto così quando il suo stato
intensivo è descrivibile con le proprietà pressione, volume specifico e temperatura,
due delle quali saranno considerate indipendenti.
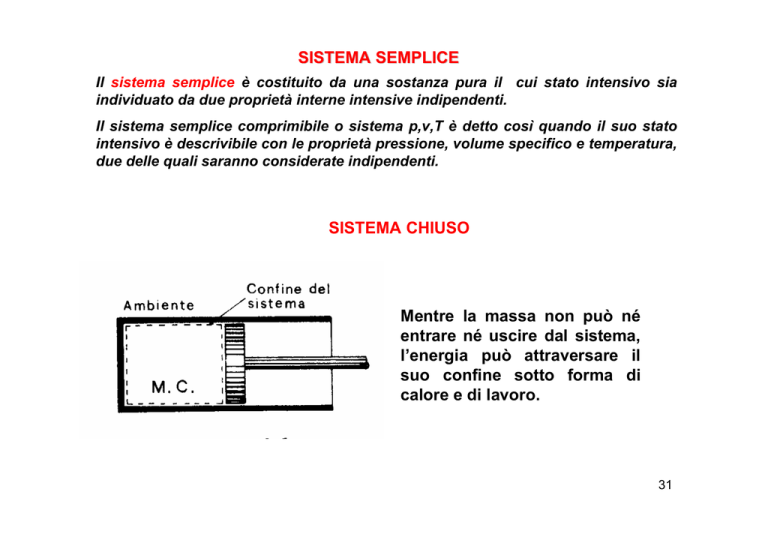
SISTEMA CHIUSO
Mentre la massa non può né
entrare né uscire dal sistema,
l’energia può attraversare il
suo confine sotto forma di
calore e di lavoro.
31
PRIMA LEGGE DELLA TERMODINAMICA
PER SISTEMI CHIUSI
Postulato-1: Un sistema semplice composto isolato in evoluzione in seguito alla
rimozione di vincoli interni raggiungerà un unico stato di equilibrio che, per un
sistema comprimibile ad un componente di massa assegnata, è completamente
determinato dai valori dell’energia U e del volume V.
L’evoluzione di sistemi isolati comporta una ridistribuzione dell’energia.
L’evoluzione di sistemi non isolati comporta l’interazione energetica di
questi con l’ambiente circostante.
L’energia è una delle proprietà fondamentali
nel campo della termodinamica.
32
PRIMA LEGGE DELLA TERMODINAMICA
PER SISTEMI CHIUSI
Postulato-2: Per un sistema termodinamico semplice comprimibile di massa
assegnata in equilibrio, è definibile una proprietà estensiva detta energia, E, che
gode della proprietà additiva; per un sistema isolato l’energia non può variare.
∆E S.I . = 0
PRIMA LEGGE DELLA TERMODINAMICA PER SISTEMI ISOLATI:
enuncia una proprietà dei sistemi isolati, ma non fornisce criteri per la
sua misurabilità; inoltre non consente alcuna analisi per sistemi che
interagiscono con l’ambiente.
33
Uno dei modi per far variare l’energia di un sistema è quello di farla
fluire attraverso il confine nella modalità lavoro, “L”.
Def. del LAVORO: il trasferimento di energia come lavoro tra due sistemi si ha
quando l’interazione è tale che l’effetto conseguente di ciascuno avrebbe potuto
essere ottenuto, per entrambi, con il solo cambiamento di quota di un peso in un
campo gravitazionale.
ATTENZIONE: il lavoro varia dipendentemente dal processo specifico (lavoro di
variazione di volume, lavoro d’elica, lavoro di pulsione) per cui contribuirà in maniera
differente alla variazione di energia del sistema tra due stati di equilibrio.
IL LAVORO NON E’ UNA PROPRIETA’ DEL SISTEMA.
DIMENSIONALMENTE IL LAVORO E’ OMOGENEO AD UN’ENERGIA.
34
Se il sistema non è isolato e, quindi, interagisce con l’ambiente circostante
nella sola modalità lavoro (il sistema è dunque adiabatico: Q=0), il lavoro è
proprio pari alla variazione di energia interna, quindi il suo valore dipende
solo dagli stati arbitrari prefissati.
Lad
sistema
ambiente
Per convenzione il lavoro è positivo se è il
sistema che compie lavoro sull’ambiente:
∆E = − L ad
Per L ad < 0 (lavoro fatto sul sistema) ⇒ E 2 > E1
Per L ad > 0 (il sistema compie lavoro) ⇒ E 2 < E1
Se il lavoro adiabatico è fatto sul sistema, l’energia del sistema
aumenterà; se è invece il sistema a cedere energia meccanica
all’ambiente, l’energia del sistema diminuirà.
35
Nello studio della Termodinamica classica è consueta la divisione dell’energia in
energia potenziale, energia cinetica (entrambe direttamente misurabili dall’esterno
del sistema in relazione alla posizione e allo stato di moto del campo
gravitazionale del sistema nel suo complesso) e in energia interna (non connessa
ad alcun riferimento esterno e conservativa) che rappresenta la somma di tutti i
contributi microscopici di energia associati alle particelle elementari che
costituiscono il sistema:
E = Ep + Ec + U
∆E = ∆E p + ∆E c + ∆U = -Lad
36
Nello studio dei sistemi chiusi si ipotizzeranno sempre nulle le
variazioni di energia potenziale e energia cinetica
∆E = ∆E p + ∆E c + ∆U = -Lad
Lad
sistema
ambiente
∆U = − L ad
37
Cosa accade se entra in gioco anche il calore Q?
Stiamo parlando di un sistema in grado di interagire nella modalità calore con
l’ambiente (sistema confinato da pareti diatermane)
IL CALORE NON E’ UNA PROPRIETA’ DEL SISTEMA.
DIMENSIONALMENTE IL CALORE E’ OMOGENEO AD UN’ENERGIA.
Per convenzione il calore è positivo se è
l’ambiente a fornire calore al sistema
L
sistema
Q
ambiente
Per Q < 0 ⇒ E 2 < E1
Per Q > 0 ⇒ E 2 > E1
∆E = ∆E p + ∆E c + ∆U = Q − L
∆U = Q − L
38
∆U = Q − L
Rappresenta
la
prima
legge
della
termodinamica per sistemi chiusi per i quali
non varino le energie cinetica e potenziale.
Stiamo considerando il caso in cui il nostro sistema è confinato da pareti
diatermane, per cui l’energia può variare in entrambe le modalità calore e lavoro.
Supponiamo che il sistema in esame si trovi in uno stato “i” iniziale di equilibrio e
che, in un secondo momento, interagisca con l’ambiente circostante facendo
fluire attraverso i confini calore e lavoro.
La sua energia interna Ui è variata passando ad un valore pari ad Uf, dove con f
si è indicato lo stato finale di equilibrio raggiunto dal sistema in seguito
all’interazione.
LIMITE DELLA PRIMA LEGGE
Qual è l’aliquota di ∆U imputabile al trasferimento di energia nella
modalità calore e quale imputabile a quello nella modalità lavoro?
39
Attenzione:
Attenzione il calore è legato ad una fenomenologia del tutto indipendente da
quella che determina il lavoro.
Se si considera un sistema confinato da pareti diatermane attraverso cui non
sono possibili flussi come lavoro, si noterà che lo stato del sistema cambia se la
temperatura del sistema è differente da quella dell’ambiente:
CAUSA DI TRASFERIMENTO DI ENERGIA NEL MODO CALORE E’ LA
DIFFERENZA DI TEMPERATURA TRA IL SISTEMA E L’AMBIENTE.
Se si considera il caso generale in cui, attraverso pareti diatermane, fluiscono sia
calore che lavoro, fissati gli stati termodinamici 1 e 2, il lavoro non è sempre lo
stesso, ma dipenderà dalle quantità di calore trasferite nel passare dallo stato1
allo stato2.
In base al postulato-2 che asserisce la conservazione dell’energia è
possibile dire che:
∆U = Q − L
Con Q si è indicato il calore che globalmente
attraversa il confine del sistema che è positivo, per
convenzione, se è in ingresso al sistema.
40
Considerando il SI in figura, costituito dai due sottosistemi A e B, con TA>TB, il verso di
trasferimento dell’energia nel modo calore è da A verso B: l’energia di A diminuisce,
quella di B aumenta dello stesso ammontare, quella del SI resterà costante.
SC1
∆Ε = 0 per SC1
SC2
SC3
∆Ε = − Q per SC 2
∆Ε = Q per SC 3
A
Q
B
Se, per assurdo, l’interazione avvenisse in senso opposto, si avrebbe:
∆Ε = 0 per SC1
∆Ε = Q per SC 2
∆Ε = − Q per SC 3
La prima legge non può fornire informazioni sul verso
dell’interazione, ma sancisce solo il Principio di conservazione
dell’energia. Tale informazione ci verrà fornita dalla seconda
legge della termodinamica che si fonda sul principio di non
conservazione della proprietà entropia.
41
Il primo principio della termodinamica
Supponiamo
Il gas assorbeche
dall’ambiente
le pareti delesterno
cilindro una
e il pistone
quantitàsiano
di calore
perfettamente
Q
Clic
per
continuare
isolanti,
e, conseguentemente,
mentre la basela
del
sua
cilindro
energia
siainterna
un conduttore
aumenta
di di
calore.
una
quantità:
Clic per iniziare
∆U=Q
Nell’espansione, il gas compie un lavoro L sull’ambiente esterno
e, conseguentemente, la sua energia interna diminuisce di una
quantità:
s
∆U=L
La variazione totale di energia interna del gas sarà dunque:
F
∆U=Q-L
PRIMO PRINCIPIO DELLA
TERMODINAMICA
42
Equazione di bilancio
Esprimiamo la prima legge della termodinamica per un sistema chiuso
mediante la seguente Equazione di bilancio per una generica proprietà
estensiva P:
Quantità di P in
ingresso al sistema
nel tempo ∆θ
+
Quantità di P generata
nel sistema nel tempo
∆θ
Quantità di P in uscita
dal sistema nel tempo
∆θ
+
=
Variazione della quantità
di P nel sistema nel
tempo ∆θ
In particolare la grandezza estensiva è l’energia.
43
Equazione di bilancio
In particolare la grandezza estensiva è l’energia che è una grandezza
conservativa per cui il termine di generazione è nullo:
Quantità di P in
ingresso al sistema
nel tempo ∆θ
Quantità di P in uscita
dal sistema nel tempo
∆θ
+
+
Quantità di P generata
nel sistema nel tempo
∆θ
=
Variazione della quantità
di P nel sistema nel
tempo ∆θ
44
Equazione di bilancio
Indichiamo con e tutte le grandezze entranti e con u tutte quelle uscenti,
l’equazione di bilancio si può così esprimere:
∑ Q+∑ L =∑
e
e
u
Q + ∑u L + ∆U
∆U = ∑e Q − ∑u Q + ∑e L − ∑u L
Qu
∆U = Q − L
Lu
Le
ambiente
che diventa
sistema
Qe
ambiente
Se Q e > Q u ⇒ Q netta > 0 essendo fornita dall' ambiente al sistema
Se L e > L u ⇒ L netta < 0 essendo l' ambiente che compie lavoro sul sistema
45
Può accadere che il flusso di energia possa essere classificato sia come
calore sia come lavoro e che si parli impropriamente di energia generata.
Esempio
Gen.
Consideriamo un resistore immerso in olio contenuto all’interno
di un recipiente adiabatico (Q=0). Il generatore fa in modo
che ci sia circolazione di corrente attraverso il resistore.
Supponendo assenza di attriti, che sia il generatori che i fili
abbiano resistenza nulla e che la massa del resistore è
trascurabile rispetto alla massa dell’olio, si otterrà:
1. Se si sceglie come sistema termodinamico l’olio ed il
resistore si può pensare che lo stato di questo sistema sia
fatto mutare con il cambiamento di quota di un peso che
metta in rotazione il generatore il flusso d’energia è
classificabile come lavoro;
2. Se si sceglie come sistema termodinamico l’olio, il resistore diventa parte
dell’ambiente ed il sistema non è più adiabatico. La differenza di temperatura che
si genera tra sistema ed ambiente farà in modo che del calore fluisca verso il
sistema;
3. Si può impropriamente pensare che non vi sia energia in ingresso, ma che vi sia
una generazione dovuta all’effetto dissipativo (Joule) del passaggio di corrente I
attraverso la resistenza elettrica R.
46
Può accadere che il flusso di energia possa essere classificato sia come
calore sia come lavoro e che si parli impropriamente di energia generata.
Esempio
Gen.
Nel primo caso, in cui il flusso di energia era classificabile
come lavoro, la prima legge della termodinamica si scrive:
∆U = − L el (lavoro ottenuto con mezzi elettrici )
Nel secondo caso, in cui il flusso di energia era classificabile
come calore, la prima legge della termodinamica si scrive:
∆U = Q
Nel terzo caso, in cui il flusso di energia era classificabile come
generazione, la prima legge della termodinamica si scrive:
dalla legge di Ohm
∆U = RI 2 ∆θ
Tempo di osservazione del fenomeno.
47
Forme differenziali della prima legge per un sistema chiuso
Per una trasformazione quasi statica ha senso parlare di cammino della
trasformazione, per cui la prima legge si può scrivere per un tratto infinitesimo di
trasformazione quasi statica:
dU = δQ − δL
in termini specifici:
du = δq − δl
lavoro elementare e calore elementare non sono differenziali esatti
48
Forme differenziali della prima legge per un sistema chiuso
Si introduce una coordinata termodinamica estensiva detta entalpia così definita:
H = U + pV
in termini specifici:
h = u + pv
Sempre con riferimento ad un tratto infinitesimo di trasformazione quasi statica,
differenziando l’espressione dell’entalpia si ottiene:
dh − vdp = du + pdv
dh = δq + (pdv − δl) + vdp
Che rappresenta la prima legge della termodinamica, per un tratto
infinitesimo di trasformazione quasi statica, in termini di variazione di
entalpia.
49












