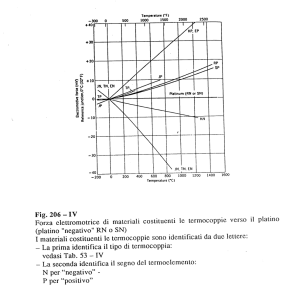
UNIVERSITA’ DEGLI STUDI DI ROMA
“TOR VERGATA”
FACOLTA’ DI INGEGNERIA
Dipartimento di Ingegneria Meccanica
DISPENSE
PER IL CORSO DI
FISICA TECNICA (AUTOMAZIONE)
Anno Accademico 2004-2005
SOMMARIO
INTRODUZIONE
1
CAP 1. TEMPERATURA
2
1.1.
EQUILIBRIO TERMICO E “PRINCIPIO ZERO” DELLA TERMODINAMICA
2
1.2.
CONCETTO DI TEMPERATURA
3
1.3.
1.4.
1.2.1.
METODO USATO FINO AL 1954
4
1.2.2.
METODO USATO DOPO IL 1954
4
LA SCALA INTERNAZIONALE DI TEMPERATURA DEL 1990 (ITS-90)
4
1.3.1.
UNITÀ DI TEMPERATURA
5
1.3.2.
DEFINIZIONE DELLA SCALA
6
STRUMENTI DI MISURA DELLA TEMPERATURA
6
1.4.1.
TERMOMETRO A GAS A VOLUME COSTANTE
6
1.4.2.
TERMOMETRO A RESISTENZA
8
1.4.3.
TERMOMETRO A RADIAZIONE
9
CAP 2. ANEMOMETRIA A FILO CALDO
12
2.1.
PRINCIPI DI FUNZIONAMENTO
12
2.2.
LA SONDA
13
2.3.
LO SCAMBIO TERMICO
14
2.4.
LE MISURE
16
TESTI CONSULTATI
18
INTRODUZIONE
Queste dispense sono destinate agli studenti del corso di FISICA TECNICA per Automazione
dell’anno accademico 2004-2005.
Si tratta di appunti che integrano e riassumono, ma non sostituiscono, le lezioni tenute in aula dal
docente per quella parte del programma definita come “applicazioni”.
Nel capitolo primo si introduce il concetto di equilibrio termico attraverso un approccio proprio
della termodinamica classica, per giungere, poi, alla definizione della temperatura e della sua scala
internazionale di misura (ITS-90). L’analisi dei principi di funzionamento dei termometri di
riferimento della ITS-90 chiude la breve trattazione.
Nel secondo capitolo, l’anemometria a filo caldo è descritta come efficace applicazione dei
principi di trasmissione del calore, specie la convezione, in uno strumento utilizzato per misure
fluidodinamiche.
Per maggiori dettagli si può fare riferimento all’elenco dei testi consultati.
IL DOCENTE
TEMPERATURA
La Termodinamica classica studia, da un punto di vista macroscopico, le interazioni tra un
sistema termodinamico e l’ambiente esterno, e gli effetti che queste determinano sul sistema stesso.
Le interazioni sono rappresentate dagli scambi di massa, lavoro e calore che avvengono, tramite il
contorno, tra il sistema e l’ambiente esterno.
Lo stato termodinamico di un sistema è definito macroscopicamente dalle seguenti variabili:
massa;
composizione chimica;
variabili interne (pressione, volume e temperatura);
variabili esterne (quota e velocità del baricentro).
Si tratta di grandezze che si riferiscono alle caratteristiche globali di un sistema, grandezze
suggerite dai nostri sensi ed, in generale, misurabili direttamente.
Nelle principali applicazioni, oggetto di studio del corso di FISICA TECNICA, per semplicità, ci
si limita a considerare sistemi con massa e composizione chimica costanti, descrivibili con una sola
coppia di coordinate termodinamiche indipendenti, determinando le altre variabili con equazioni
aggiuntive di natura sperimentale, note come equazioni costitutive o di stato (esempio: equazione di
stato dei gas perfetti).
Riguardo agli stati termodinamici, la termodinamica classica si occupa di stati di equilibrio, ovvero
di stati in cui il sistema raggiunge un equilibrio interno ed esterno di tipo meccanico, chimico e
termico.
1.1.
EQUILIBRIO TERMICO E “PRINCIPIO ZERO” DELLA TERMODINAMICA
Gli esperimenti mostrano che l’esistenza di uno stato di equilibrio in un sistema dipende dal fatto
che questo abbia vicino altri sistemi, e dalla natura delle pareti che li separano.
Detta (x,y) la coppia di coordinate che descrive lo stato termodinamico, considerando due sistemi
A, con stato (x1,y1), e B, con (x2,y2), a contatto attraverso una parete che li separa, possono
verificarsi due situazioni:
1. le coordinate termodinamiche non variano (la parete viene detta adiabatica);
2. le coordinate termodinamiche dei due sistemi cambiano spontaneamente sino a raggiungere
dei valori di equilibrio per tutto il sistema (la parete viene detta diatermica o conduttrice).
Fisica Tecnica (Automazione)
CAP 1 - Temperatura
3
Quindi, l’equilibrio termico è quello stato, caratterizzato da certi valori delle coordinate, che due o
più sistemi raggiungono quando sono messi in comunicazione tra loro tramite una parete
conduttrice.
Consideriamo ora due sistemi A e B, separati da una parete adiabatica, ciascuno dei quali è a
contatto, tramite una parete conduttrice, con un terzo sistema C. Supponiamo l’insieme contenuto
entro pareti adiabatiche. L’esperienza mostra che i due sistemi raggiungono l’equilibrio con il terzo e
che non si ha poi alcun cambiamento se la parete adiabatica tra A e B è sostituita con una
conduttrice.
Tale risultato può essere sintetizzato con l’enunciato del principio zero della termodinamica:
“due sistemi in equilibrio termico con un terzo sono in equilibrio termico tra loro”.
1.2.
CONCETTO DI TEMPERATURA
La condizione di equilibrio termico si può caratterizzare facendo riferimento ad un’unica
proprietà chiamata temperatura.
Definendo con isoterma il luogo di tutti i punti che rappresentano stati in cui il sistema si trova in
equilibrio termico con uno stesso stato di un altro sistema, si può affermare che tutti gli stati che
appartengono a isoterme corrispondenti dei vari sistemi hanno in comune la proprietà di essere in
equilibrio termico l’uno con l’altro. Questo stesso concetto, in formulazione matematica, diventa:
t = f A ( x, y ) = f B ( x ', y ') = f C ( x '', y '') ,
dove il valore comune di queste equazioni è detto temperatura empirica dei tre sistemi considerati e
la relazione t = f A ( x, y ) non rappresenta altro che l’equazione di un isoterma del sistema A.
Per definire la temperatura come grandezza fondamentale, è necessario un segno di maggiore o
minore quando i valori non sono uguali. Tale segno è dato dal secondo principio della termodinamica:
“un sistema ha una temperatura maggiore di quella dell’altro sistema quando dal primo al secondo si ha una
trasmissione spontanea del calore”.
Per rappresentare la temperatura con un numero occorre fissarne una scala empirica, scegliendo
come campione un qualunque sistema di coordinate (X,Y), definito termometro, ed adottando un
insieme di regole e procedure per associare un valore numerico alla temperatura corrispondente ad
ognuna delle isoterme del sistema scelto. Lo stesso numero sarà poi associato alla temperatura di
qualunque altro sistema si trovi in equilibrio termico con il termometro.
Come conseguenza, si possono avere differenti scale di temperatura in relazione allo strumento
utilizzato per misurarla. Per semplicità, si scelgono termometri in cui è una sola la coordinata che
varia con le isoterme, rimanendo costante la seconda. In tale caso, supponendo la temperatura
funzione della coordinata X, la X prende il nome di caratteristica termometrica e la scala di temperatura è
fissata dalla forma della funzione termometrica θ(X).
Tabella 1.1. -
Termometri e caratteristiche termometriche.
Termometro
Termometro a gas (volume costante)
Resistore elettrico (d.d.p. costante)
Termocoppia (d.d.p. costante)
Termometro a dilatazione (liquido o solido)
Vapore di elio (saturo)
Termometro a radiazione
Sale paramagnetico
Caratteristica termometrica
Pressione
Resistenza elettrica
F.e.m termoelettrica
Lunghezza (volume)
Pressione
Potere emissivo
Suscettività magnetica
Nella tabella 1.1 sono elencati alcuni importanti tipi di termometro, assieme alle rispettive
caratteristiche termometriche, ovvero le proprietà (o grandezze) usate per la misura della
temperatura. Indichiamo con X una qualunque delle caratteristiche termometriche riportate in
Fisica Tecnica (Automazione)
CAP 1 - Temperatura
4
tabella 1 e definiamo la scala di temperatura in modo che la temperatura θ sia direttamente
proporzionale a X.
Supponendo, arbitrariamente, una relazione lineare tra temperatura e coordinata X, si scrive (con
Y=cost):
ϑ( X ) = a ⋅ X
(1.1)
con a costante arbitraria. Dunque, prendendo due temperature T1 e T2 , vale la seguente relazione
ϑ( X1 ) X1
=
(1.2)
ϑ( X 2 ) X 2
Per determinare la temperatura θ(X) di un sistema si può seguire uno dei seguenti procedimenti.
1.2.1.
METODO USATO FINO AL 1954
Occorre innanzitutto definire due punti fissi, ovvero due stati termodinamici facilmente
riproducibili di un sistema campione. Candidati ad essere punti fissi sono:
la temperatura alla quale il ghiaccio puro è in equilibrio con acqua satura d’aria alla
pressione di una atmosfera (punto del ghiaccio);
la temperatura di equilibrio tra acqua pura e vapor d’acqua puro alla pressione di una
atmosfera (punto del vapor d’acqua).
Applicando la (1.2), il termometro è messo dapprima in contatto col sistema del quale si vuole
conoscere la temperatura θ(X), e poi con il sistema campione ad uno dei due punti fissi:
ϑ( X1 ) X1
(1.3)
=
ϑ( X )
X
Successivamente, sempre per la stessa temperatura θ(X) e per l’altro punto fisso, si ha:
ϑ( X 2 ) X 2
(1.4)
=
ϑ( X )
X
Sottraendo la (1.4) dalla (1.3), ricavando θ(X) si ottiene:
ϑ( X1 ) − ϑ( X 2 )
=X
ϑ( X ) =
(1.5)
X1 − X 2
Attribuendo un numero arbitrario di gradi all’intervallo di temperatura θ ( X 1 ) − θ ( X 2 ) (ad
esempio 100 gradi), ne segue che il valore di temperatura cercato può essere calcolato con la (1.5)
misurando i tre valori X, X1 e X2.
1.2.2.
METODO USATO DOPO IL 1954
Dal 1954 si utilizza un solo punto fisso: il cosiddetto punto triplo dell’acqua, cioè quello stato
dell’acqua pura in cui si ha equilibrio fra ghiaccio, liquido e vapore. Alla temperatura di questo stato
viene attribuito per convenzione il valore di 273.16 K.
Indicando con l’indice 3 il punto triplo dell’acqua, si scrive:
ϑ( X )
X
(1.6)
=
ϑ( X 3 ) X 3
con ϑ ( X 3) = 273.16 K e quindi
X
ϑ ( X ) = 273.16
(1.7)
X3
1.3.
LA SCALA INTERNAZIONALE DI TEMPERATURA DEL 1990 (ITS-90)
I punti fissi, tra i quali quelli introdotti al paragrafo precedente, sono sistemi in cui la temperatura
rimane stabile per tempi lunghi, fino a quando le condizioni esterne non cambiano la natura del
sistema stesso. In genere sono punti tripli di sostanze pure, oppure punti di solidificazione,
condizione in cui la temperatura dipende debolmente dalla pressione.
Fisica Tecnica (Automazione)
CAP 1 - Temperatura
5
I punti fissi (vedere figura 1.1) e gli strumenti di riferimento da utilizzare nelle misure di temperatura
sono stati previsti dalla ITS90 (International Scale Temperature of 1990), norma pubblicata dal
CIPM (Comitato Internazionale di Pesi e Misure).
Figura 1.1. - Punti fissi di alcune sostanze più comunemente usati.
1.3.1.
UNITÀ DI TEMPERATURA
Secondo la ITS90 il Kelvin (K) è definito come 1/273,16 della temperatura termodinamica del
punto triplo dell’acqua.
Il grado Celsius (°C) è definito dalla relazione t (°C)= T (K) – 273,15 e 0°C corrisponde alla
temperatura di fusione del ghiaccio.
Fisica Tecnica (Automazione)
1.3.2.
CAP 1 - Temperatura
6
DEFINIZIONE DELLA SCALA
L’ITS90 prevede di misurare la temperatura con i seguenti strumenti nei seguenti intervalli:
Tabella 1.2. -
Scala Internazionale di Temperatura: intervalli e termometri.
Intervallo
Termometro
0.65 K ÷ 5.0 K
3.0 K ÷ 24.5561 K
(punto triplo del neon)
Caratteristica termometrica
Equazione dell’equilibrio temperaturapressione di vapore dell’elio
Termometro a gas
Pressione
Termometro a resistenza al platino
Resistenza elettrica
(punto triplo dell’idrogeno)
13.8003 K ÷ 961.78 °C
(punto di solidificazione dell’argento)
Pirometro monocromatico, tarato ad
Al di sopra di 961.78°C
uno dei seguenti punti di solidificazione:
Ag (961.78°C)
Au (1064,18°C)
Potere emissivo
Cu (1084,62°C)
1.4.
STRUMENTI DI MISURA DELLA TEMPERATURA
Nei paragrafi seguenti si accennerà brevemente alle caratteristiche ed ai principi di funzionamento
di tre tipi di termometri: il termometro a gas, il termometro a resistenza ed il pirometro.
1.4.1.
TERMOMETRO A GAS A VOLUME COSTANTE
Una scala di temperatura termodinamica completamente indipendente dal tipo di caratteristica
termometrica scelta è quella proposta da Lord Kelvin nel 1848, basata sul ciclo di Carnot. Per questo
ciclo ideale, dalla definizione del rendimento del sistema motore termico reversibile, si ha la
relazione
Q2 T2
=
(1.8)
Q1 T1
dove le quantità di calore scambiate con le due sorgenti e le temperature di queste sono indicate con
i pedici 1 e 2.
Avendo definito il rapporto tra le temperature, scegliendo un punto fisso, la scala di temperatura
sarebbe completamente definita. Questa scala, pur essendo indipendente dalle proprietà dei materiali
(ovvero dal tipo di fluido che evolve nel motore), è, di fatto, irrealizzabile essendo il ciclo di Carnot
solo una astrazione teorica.
Si dimostra, comunque, che una scala di temperatura definita da un termometro a gas ideale è
identica alla scala termodinamica proposta da Kelvin, quindi, fissato lo stesso punto fisso (punto
triplo dell’acqua) come riferimento, le due scale sono anche numericamente identiche.
Il termometro a gas perfetto a volume costante mantiene una fissata massa di gas a volume
costante e misura le variazioni di pressione dovute ai cambiamenti di temperatura, viceversa per
quello a pressione costante, in cui i cambiamenti di volume sono proporzionali a quelli di
temperatura. In ogni caso, dalla equazione di stato dei gas perfetti si deduce che il rapporto tra le
temperature è pari a quello delle pressioni, ovvero, a quello dei volumi.
Tuttavia, anche la condizione di gas perfetto è un modello matematico e non una reale sostanza,
dunque, per ottenere una scala di temperatura fisicamente realizzabile, si devono usare gas reali nei
Fisica Tecnica (Automazione)
CAP 1 - Temperatura
7
termometri. La lettura, sia essa del volume o della pressione, dovrà essere corretta per tener conto
della deviazione dal comportamento di gas ideale.
La figura 1.2 mostra lo schema di principio di un termometro a gas (tipicamente 4He o 3He) a
volume costante. I materiali impiegati, i dettagli costruttivi e le dimensioni variano nei diversi
laboratori o istituti e dipendono dalla natura del gas e dall’intervallo di temperatura in cui si pensa di
utilizzare il termometro.
1
M
2
B
Figura 1.2. - Termometro a gas a volume costante.
La massa di gas, contenuta nel bulbo B, è in comunicazione, tramite un capillare, con un tubo
manometrico contenente mercurio. Il volume del gas viene mantenuto costante alzando o
abbassando il serbatoio M, controllando che l’interfaccia tra mercurio e gas sia su un livello fissato
del tubo, livello individuato in figura dall’indice 1.
Ponendo il bulbo a contatto termico con il sistema di cui si deve misurare la temperatura e poi a
contatto con acqua al punto triplo, dalla misura delle differenze di quota tra i livelli 1 e 2, si ricavano
le due pressioni assolute p e pT, determinate come somma tra la pressione relativa e quella
atmosferica.
La temperatura cercata sarà poi espressa con la relazione (1.7), da cui
ϑ ( p ) = 273,16 ⋅
p
pT
(1.9)
Trattandosi di un gas reale in luogo di uno perfetto, nella relazione (1.9) il rapporto tra le
pressioni dipende dal tipo di sostanza e dalla massa del gas nel bulbo.
La figura 1.3 mostra l’andamento della pressione per termometri, con diversi tipi di gas, posti a
contatto con vapor d’acqua che sta condensando. Fissando l’attenzione ad un solo tipo di gas, si
nota che diminuendone la massa presente nello strumento, la pressione di riferimento pT tende a
diminuire anch’essa. Procedendo per successive sottrazioni di massa ed estrapolando il valore per pT
che tende a zero (assenza di materia), si nota che, indipendentemente dal tipo di gas presente, tutti i
termometri tendono alla stessa temperatura.
Fisica Tecnica (Automazione)
CAP 1 - Temperatura
8
PT,
Figura 1.3. - Risposte di un termometro a gas a volume costante a contatto con del vapor d’acqua in condensazione:
ogni curva riguarda un diverso gas reale impiegato nello strumento.
Da questa osservazione, si può riscrivere la (1.9) con la seguente relazione:
⎛ p ⎞
⎟
pT →0
⎝ pT ⎠
ϑ ( p ) = 273,16 ⋅ lim ⎜
1.4.2.
(1.10)
TERMOMETRO A RESISTENZA
Le termoresistenze sono conduttori metallici (di solito nichel, platino o rame) che cambiano la
loro resistenza elettrica con la temperatura in modo monotono.
Figura 1.4. - Variazione della resistenza R con la temperatura T per alcuni materiali usati nei termometri a resistenza.
L’elemento sensibile può essere messo direttamente a contatto col sistema del quale si vuole
conoscere la temperatura, oppure, specie nelle misure in fluidi, essere protetto da un bulbo in acciaio
inossidabile, per prevenire l’azione della corrosione.
La lettura si effettua con maggiore accuratezza usando la tecnica della misura di resistenza a
quattro terminali, ponendo la resistenza dell’elemento sensibile in serie con un resistore campione.
Facendo passare nel circuito una corrente costante nota (pochi milliampere), dalla misura di caduta
di tensione sul resistore campione si valuta la corrente che scorre nel circuito, dopodiché, misurando
la differenza di potenziale sull’elemento sensibile è possibile ricavarne la resistenza elettrica.
Fisica Tecnica (Automazione)
CAP 1 - Temperatura
9
Dapprima si misura la resistenza di riferimento R0 quando il termometro si trova al punto triplo
dell’acqua (273,16 K) e poi, alla temperatura incognita, la resistenza R. Il rapporto tra le due
resistenze è la resistenza indotta, rappresentata da una equazione del tipo
R
= 1 + a1T + a2T 2 + ... + anT n
R0
(1.11)
Il numero di termini della (1.11) dipende dal materiale, dall’accuratezza richiesta e dall’intervallo
di temperatura coperto. I coefficienti dell’equazione e della sua inversa si ottengono dalla norma
ITS-90 e da un opportuno processo di taratura.
Figura 1.5. - Circuito per misurare la resistenza di un termometro a resistenza percorso da una corrente costante.
Pregi dello strumento:
è uno strumento stabile: è sempre preciso e piuttosto accurato, quindi non va tarato di
continuo;
ha un’uscita elettrica, per questo motivo è particolarmente raccomandato per misure
industriali di precisione in un campo compreso fra i –200°C e +700°C e talvolta pure
fino a 1100°C;
si presta molto bene per esser utilizzato come termografo soprattutto per registrare un
temperatura a distanza o per seguire da un centro di controllo la marcia di uno o più
forni.
Principali difetti:
è piuttosto costoso;
il riscaldamento per effetto Joule può essere consistente (il calore dissipato è Q = R ⋅ I 2 )
e può rovinare il dispositivo;
presenta un’inerzia termica in quanto non è eccessivamente piccolo.
1.4.3.
TERMOMETRO A RADIAZIONE
Il pirometro è uno strumento capace di intercettare e misurare la radiazione termica emessa da un
corpo, al fine di determinarne la temperatura superficiale, senza la necessità di porre il termometro a
contatto con il corpo stesso.
Da un punto di vista costruttivo, il pirometro è costituito essenzialmente da un sistema ottico che
focalizza la radiazione termica su un elemento sensibile, la cui risposta è in genere di natura elettrica.
Al sensore e all’ottica del sistema si aggiungono i filtri e tutte le componenti elettroniche necessarie
all’elaborazione del segnale elettrico.
La base teorica del funzionamento del pirometro è rappresentata dalle ben note leggi
dell’irraggiamento, in particolare quelle di Planck, di Wien e di Kirchhoff.
I pirometri possono essere classificati in:
Fisica Tecnica (Automazione)
CAP 1 - Temperatura
10
termometri a radiazione ampia, sensibili a lunghezze d’onda che vanno da 0.3 μm a 2.5 o 20
μm, in funzione delle caratteristiche del sistema ottico;
termometri a radiazione parziale, in cui la stretta banda delle lunghezze d’onda è scelta in
funzione della sopracitata legge di Wien ed è ottenuta con opportuni filtri;
termometri a rapporto di radiazione, caratterizzati dalla sensibilità a due diverse strette bande
di lunghezze d’onda, dei quali il pirometro a due colori ne rappresenta un caso
particolare;
pirometro ottico, caso particolare di quello a radiazione parziale, caratterizzato dalla
presenza di una lampada a filamento e sensibile sostanzialmente ad una sola lunghezza
d’onda;
termometro a fibre ottiche.
Tenuto conto della classificazione e delle basi teoriche, volendo specificare con maggiore
dettaglio il funzionamento, l’equazione (1.12) rappresenta il flusso termico emesso da un corpo nero
per unità di superficie e di lunghezza d’onda nel vuoto, ovvero il potere emissivo monocromatico:
C1
E nλ (T ) =
(1.12)
⎛ C2 ⎞ ⎤
5 ⎡
λ ⋅ ⎢exp⎜
⎟ − 1⎥
⎣ ⎝ λ ⋅T ⎠ ⎦
con C 1 = 3.741 ⋅ 10 −16 Wm 2 e C 2 = 1.439 ⋅ 10 −2 mK .
Nella realtà, essendo il corpo nero una astrazione matematica, occorre valutare l’emittenza
monocromatica emisferica ελ dei corpi reali che emettono, ed, inoltre, la effettiva radiazione che
giunge sul sensore, considerando i coefficienti di trasmissione (trasmittanza) τλ dei vari mezzi
incontrati dalla radiazione termica (aria, sistema ottico costituito da lenti e specchi, filtri) prima di
giungere al rivelatore sensibile.
E’ necessario, poi, introdurre, rispetto la superficie che riceve la radiazione, l’angolo solido ω ad
essa sotteso e la conseguente dipendenza dall’angolo θ secondo cui la superficie ricevente è vista da
quella emettente. Inoltre, supponendo valido per semplicità il teorema del coseno di Lambert,
l’intensità di radiazione I nλ (o radianza), nel caso di corpi neri, può essere scritta come
E (T )
(1.13)
I nλ ( T ) = nλ
π
mentre per i corpi reali che emettono in un mezzo diverso dal vuoto, tenuto conto della (1.12), si ha
ελ ⋅C1
1
(1.14)
I λ (T ) = ⋅
π 2 5 ⎡ ⎛ C2 ⎞ ⎤
nλ ⋅ λ ⋅ ⎢exp ⎜
⎟ − 1⎥
⎝ nλ ⋅ λ ⋅ T ⎠ ⎦
⎣
dove nλ indica l’indice di rifrazione del mezzo.
Dunque, integrando la (1.14) per la banda Δλ di lunghezze d’onda propria del tipo di pirometro,
per la superficie A dell’emettitore e per l’angolo solido interessato, il segnale S(T) di uscita, in Volt,
del sensore è esprimibile con la relazione
S( T ) = ∫ ∫ ∫ σ λ ( λ , Ts ) ⋅τ λ ( λ , Tm ) ⋅ I λ ( T ) ⋅ cos ϑ ⋅ d ω ⋅ d λ ⋅ dA
(1.15)
A Δλ ω
dove si è indicato con σλ e Ts rispettivamente la risposta spettrale e la temperatura del sensore,
mentre con Tm la temperatura dei mezzi materiali attraversati dalla radiazione.
Nella (1.14), definite le caratteristiche geometriche e costruttive del pirometro, misurato il segnale
in Volt, l’unica incognita è la temperatura cercata.
Per la taratura dello strumento, si sceglie un corpo nero, opportunamente realizzato in
laboratorio, posto ad una temperatura costante nota, ovvero un punto fisso, ad esempio, la
temperatura al punto di solidificazione del rame.
La temperatura incognita T della superficie generica sarà, dunque, individuata dal rapporto
Fisica Tecnica (Automazione)
S(T )
=
S ( TCu )
CAP 1 - Temperatura
∫ ∫ ∫ σ λ ( λ ) ⋅τ λ ( λ ) ⋅ I λ (T ) ⋅ cosϑ ⋅ dω ⋅ d λ ⋅ dA
A ω Δλ
∫∫
∫ σ λ ( λ ) ⋅τ λ ( λ ) ⋅ I nλ (TCu ) ⋅ cosϑ ⋅ d ω ⋅ d λ ⋅ dA
11
(1.16)
A ω Δλ
La soluzione di questa equazione in T è piuttosto complessa, ma con alcune ipotesi
esemplificative è possibile ottenerne una buona approssimazione.
Si considera, infatti, trascurabile la dipendenza della radianza dall’angolo solido e dalla superficie
di emissione, e, puntando lo strumento secondo la stessa inclinazione sia per il corpo nero che per la
superficie reale, sono eguali, in entrambi i casi, la trasmittanza del sistema ottico e la sensibilità del
rilevatore. Infine, occorre definire la lunghezza d’onda equivalente λe in base alla relazione
1
1 λe
=
+
⋅ ln ε λe
(1.17)
T Tλe C 2
dove T è la temperatura termodinamica del corpo, mentre la Tλe è detta temperatura di radianza di
un radiatore reale, equivalente alla temperatura di un corpo nero avente la stessa intensità di
radiazione di quello reale, alla stessa lunghezza d’onda.
Introdotta la lunghezza d’onda equivalente, nella (1.16) si può eliminare anche la dipendenza dalla
banda di lunghezza d’onda del pirometro, per cui si ottiene
⎛ C2 ⎞
exp ⎜
⎟ −1
I λe ( T )
nλ ⋅ λe ⋅ T ⎠
S(T )
⎝
(1.18)
=
=
S ( TCu ) I nλe ( TCu )
⎛
⎞
C2
exp ⎜
⎟ −1
⎝ nλ ⋅ λe ⋅ TCu ⎠
dalla quale è possibile ricavare la temperatura cercata.
Nell’utilizzo dello strumento, uno dei maggiori problemi è rappresentato dalla determinazione
dell’emissività del corpo che emette la radiazione: un semplice foro nella superficie può
rappresentare spesso un’approssimazione più che sufficiente per i calcoli (la differenza da un corpo
nero ideale di un foro con diametro un terzo della profondità è dell’ordine del 1%).
Pregi dello strumento:
è uno strumento senza contatto;
misura temperature termodinamiche molto elevate.
Principali difetti:
per ottenere elevate precisioni sono necessarie laboriose e lunghe tarature, da ripetere
periodicamente;
occorre conoscere (o misurare) l’emissività delle superfici emettenti.
Figura 1.6. - Esempi di pirometri fissi e portatili.
ANEMOMETRIA A FILO CALDO
2.1.
PRINCIPI DI FUNZIONAMENTO
Con il termine anemometria è da intendersi lo studio dei metodi e delle tecniche necessarie per la
misura di velocità di flussi. In particolare, l’anemometria a filo caldo, o più in generale anemometria
termica, si basa sullo scambio termico convettivo tra un elemento sensibile riscaldato e il flusso che
lo investe, flusso del quale si vuole conoscere la velocità.
Figura 2.1. - “Catena delle misure fluidodinamiche”.
L’anemometro termico è costituito da tutto un sistema di strumenti che rende possibile la misura:
sonda, supporti, cavi, filtri e amplificazione.
Il segnale ottenuto dall’anemometro è poi trasferito ad un sistema di acquisizione dati e da questi
ad un personal computer, dove i risultati sono poi processati.
La catena della misura è riportata sinteticamente nello schema di figura 2.1.
Fisica Tecnica (Automazione)
CAP 2 - Anemometria a filo caldo
13
Gli anemometri possono operare secondo due diversi modi:
a corrente costante (CC mode), in cui la temperatura della sonda varia;
a temperatura costante (CT mode), in cui la resistenza della sonda e quindi la sua
temperatura sono mantenute costanti dalla variazione della corrente applicata.
Nella maggior parte delle applicazioni si opera in “CT mode”.
Il sensore utilizzato negli anemometri ha un piccolo elemento a resistenza che è scaldato e
mantenuto ad elevate temperature (intorno ai 250 °C). Le sonde più comuni sono generalmente di
due tipi:
a filo caldo;
a film caldo.
Il sensore, collocato su una sonda a sua volta connessa all’anemometro mediante un cavo coassiale,
costituisce una delle resistenze di un ponte di Wheatstone (figura 2.2), ponte che in principio deve
essere bilanciato a temperatura ambiente.
Figura 2.2. - Il ponte di Wheatstone del circuito dell’anemometro.
Quando l’anemometro è nella fase di acquisizione, il flusso che investe il sensore provoca una
variazione della sua resistenza proporzionale alla velocità del fluido e quindi un aumento del
voltaggio misurato sulla diagonale orizzontale del ponte. Lo strumento avverte questo cambiamento
e risponde applicando una differenza di potenziale sulla diagonale verticale, producendo una
corrente che, fluendo nella sonda, ne provoca un riscaldamento tale da ristabilire di nuovo
l’equilibrio. Come conseguenza, il filo o il film tornano ad avere la temperatura e resistenza iniziali,
mentre il voltaggio del ponte è necessariamente cambiato: questo incremento di d.d.p. rappresenta il
segnale di uscita dell’anemometro, letto poi dal sistema di acquisizione.
Tale differenza di potenziale, previa opportuna taratura, è la misura della velocità del getto.
2.2.
LA SONDA
L’elemento sensibile dello strumento può essere a filo o film caldo.
Le dimensioni standard di un filo sono un diametro di 4-5 μm per una lunghezza di 1.25 mm. I
materiali che costituiscono il singolo filamento sono il tungsteno, il platino, leghe di platino e rodio
(90-10%) e leghe di platino e iridio (80-20%).
Le sonde a film caldo sono, invece, costituite da un film di platino o nickel dello spessore di circa
0.1 μm, depositato, con un processo catodico, su un sottostrato isolante cilindrico di quarzo. Il film
è poi coperto con un sottile strato di 1-2 μm di quarzo, il quale lo protegge da particelle abrasive e lo
isola elettricamente. Il passaggio della corrente nel film è garantito dal collegamento con supporti
rivestiti di oro.
Fisica Tecnica (Automazione)
CAP 2 - Anemometria a filo caldo
14
Inoltre, indipendentemente dal tipo di sensore, ciascuna sonda può essere costituita da uno o più
elementi sensibili, secondo il numero di componenti di velocità che si intendono misurare.
Figura 2.3. - Esempio di sonda anemometrica a film caldo.
2.3.
LO SCAMBIO TERMICO
Supponiamo di riferirci, per semplicità espositiva, al caso di un anemometro ad un filo caldo,
fermo restando che la trattazione è valida anche per trasduttori del tipo film caldo.
Lo scambio termico tra il filo e il fluido dipende sia dalle proprietà termofisiche del fluido
(densità, viscosità, conduttività termica, calore specifico, etc..) che dai parametri propri del flusso
(vettore velocità, pressione, etc…).
Facendo riferimento alla figura 2.4, si può scrivere la seguente equazione di bilancio termico al
tratto dx dell’elemento sensibile dell’anemometro:
(2.1)
dQ e = dQ c + dQ k + dQ r + dQ a
dove i pedici stanno per:
“e”= calore generato dal passaggio di corrente;
“c”= calore ceduto al flusso per convezione;
“k”= calore scambiato per conduzione sui supporti;
“r”= calore scambiato per irraggiamento;
“a”= calore assorbito.
Ciascun contributo può essere quantificato come segue:
I 2χ f
dQe =
dx
(2.2)
Af
(2.3)
dQ = h ⋅ (π ⋅ d ⋅ dx ) ⋅ (T − T )
c
f
a
∂ Tf
dQ k = −κ f A f
dx
∂x 2
dQ r = σ ⋅ ε ⋅ (π ⋅ d ⋅ dx ) ⋅ (T f 4 − Ts 4 )
2
(2.4)
(2.5)
∂T f
dQ a = ρ f ⋅ c f ⋅ Af
dx
(2.6)
∂t
dove si è indicato con
χ f , ρ f , κ f , c f , A f , T f rispettivamente la resistività, la densità, la conducibilità termica, il
calore specifico, la sezione e la temperatura del filo;
Ta la temperatura del flusso;
Ts la temperatura dell’ambiente esterno al filo;
Fisica Tecnica (Automazione)
CAP 2 - Anemometria a filo caldo
15
σ , ε la costante di Stefan-Boltzmann e l’emittenza totale del sensore alla temperatura
del filo.
Figura 2.4. - Geometria di un filo caldo (sopra) e bilancio termico su un suo elemento infinitesimo (sotto).
Considerando che in condizioni stazionarie il termine con pedice “a” scompare, in prima
approssimazione, riferendoci ad un filo di lunghezza infinita, si possono trascurare i contributi
dovuti all’irraggiamento e alle perdite per conduzione sui supporti. Dunque, l’equazione (2.1)
diventa:
(2.7)
I 2 R f ,∞ = h ⋅ π ⋅ d ⋅ l ⋅ (T f ,∞ − Ta )
l
resistenza del filo.
Af
Supponendo un andamento lineare della resistenza del filo rispetto la temperatura cui si trova, si ha
la relazione
con
R f ,∞ = χ f ⋅
Fisica Tecnica (Automazione)
CAP 2 - Anemometria a filo caldo
R f = R0 ⎡⎣1 + α 0 ⋅ (T f − T0 ) ⎤⎦
16
(2.8)
dove α 0 è una costante che dipende dal tipo di materiale del sensore e dalla temperatura di
riferimento T0 .
Dalla (2.8), si ricava
(2.9)
R f − Ra = R0 ⎡⎣1 + α 0 ⋅ (T f − T0 ) ⎤⎦ − R0 ⎡⎣1 + α 0 ⋅ (Ta − T0 ) ⎤⎦ = R0 ⋅ α 0 ⋅ (T f − Ta )
la quale, invertita, fornisce
R f − Ra
= (T − T
)
f
a
α 0 ⋅ R0
Considerando, inoltre, una legge empirica di scambio termico per convezione del tipo
h⋅d
Nu =
= 0.42 Pr 0.20 + 0.57 Pr 0.33 Re0.50
k
la (2.7) si riscrive
I 2 R f ,∞ = h ⋅ d ⋅ π ⋅ l ⋅
R f ,∞ − Ra
α 0 ⋅ R0
= π ⋅ l ⋅κ ⋅
R f ,∞ − Ra
α 0 ⋅ R0
⋅ Nu
(2.10)
(2.11)
(2.12)
ovvero
I 2 R f ,∞
R f ,∞ − Ra
= A + BU 0.5
nella quale
A = 0.42 Pr 0.20 ⋅
B = 0.57 Pr
Re =
ρ dU
μ
0.33
(2.13)
πκ l
α 0 R0
⎡ ρd ⎤
⋅⎢
⎥
⎣ μ ⎦
(2.14)
0.50
⋅
πκ l
α 0 R0
(2.15)
(2.16)
Nel caso di filo di lunghezza finita, le perdite per conduzione ai supporti non possono essere
trascurate. Nella pratica questo è raggiunto modificando la (2.13) in
I 2Rf
= A + BU n
(2.17)
R f − Ra
L’equazione (2.17) può essere infine ricondotta alla relazione
(2.18)
E 2 = A + BU n
nota come legge di King, dove “E” è la tensione letta.
La taratura dello strumento consiste nella determinazione delle costanti A, B ed n. La velocità
sarà poi misurata e calcolata invertendo la relazione (2.18): si misura E e si calcola U.
2.4.
LE MISURE
Nel completare la descrizione dello strumento, va sottolineato che, nel caso di filamento unico,
ciò che si può valutare è il solo valore efficace del vettore velocità, ovvero il suo modulo, senza avere
quindi la possibilità di apprezzarne le sue componenti cartesiane.
In particolare, la velocità misurata con la (2.18) altro non è che la sua componente efficace data
dalla seguente relazione:
Ve = U N2 + k 2 ⋅UT2 + h2 ⋅U B2
dove:
E 2 = A + B ⋅ Ve n → Ve = velocità efficace avvertita dal filo, legata al vettore velocità V ;
(2.19)
Fisica Tecnica (Automazione)
CAP 2 - Anemometria a filo caldo
U N = componente normale al sensore;
U T = componente tangenziale al sensore;
U B = componente binormale al sensore;
k = 0.0 ÷ 0.2 ;
h = 1.0 ÷ 1.2 .
Figura 2.5. - Componenti della velocità nel sistema di riferimento solidale con il filo.
17
TESTI CONSULTATI
[1] F. Gori, “Lezioni di Termodinamica”, CittàStudiEdizioni, (2000)
[2] M. W. Zemansky, “Calore e Termodinamica”, Zanichelli Bologna Editore, (1985)
[3] T. J.Quinn, “Temperature”, Academic Press, (1983)
[4] T. Preston, “The International Temperature Scale of 1990 (ITS-90)”, Metrologia, 27, 3-10 (1990)
[5] E. O. Doebelin, “Measurements Systems Application and Design”, McGraw-Hill, (1990)
[6] F. Kreith, “Principi di trasmissione del calore”, Liguori Editore, (2002)
[7] http://www.omega.com/literature/transactions/volume1/historical1.html, sito internet della
Omega Engineering, Inc. (consultato nel febbraio 2005)
[8] C. E. Gibson, B. K. Tsai, A. C. Parr, “NIST Measurements Services: Radiance Temperature
Calibrations”, Natl. Inst. Stand. Technol. Spec. Publ. 250-43, 123 pages, (Jan. 1998)
[9] H. H. Bruun, “Hot Wire Anemometry Principles and Signal Analysis”, Oxford University Press,
(1995)
[10] “AN-1003 Hot wire & film anemometry system”, manuale d’uso dell’anemometro della TSI, Inc.