modelli di drude e di sommerfeld

MODELLI DI DRUDE E DI SOMMERFELD
BANDE PIENE E SEMIPIENE
In base al principio di Pauli non possono esistere in uno stesso sistema due elettroni con tutti i
numeri quantici uguali. Poiché una banda può ospitare N diversi valori di k, e gli stati di spin
dell'elettrone sono 2, i posti liberi sono 2N. Se ogni atomo può mettere a disposizione 2 elettroni di
valenza (cioè nell'orbitale più esterno) per ogni sito, si formerà nel solido una banda di valenza
completamente piena. Il solido a T=0 sarà un isolante, perché sotto l'azione del campo elettrico
l'elettrone, per potersi muovere, deve poter cambiare il suo vettore d'onda k; ma siccome tutti gli
stati con k diversi sono pieni, ciò non potrà avvenire. La banda vuota superiore infatti (banda di
conduzione) si trova al di là di una gap di stati proibiti. Se però la gap è relativamente piccola, a
temperatura finita le eccitazioni termiche possono promuovere nella banda superiore elettroni che a
quel punto trovano un'abbondanza di stati vuoti e possono condurre. Un tale sistema è un
semiconduttore.
Se gli atomi del cristallo sono monovalenti, come nei metalli alcalini, solo N stati possono venire
riempiti e si formerà una banda semipiena. A T= 0, per il principio di Pauli, tutti gli stati vengono
riempiti a coppie fino a un'energia massima che si chiama energia di Fermi EF. Al di sopra di EF gli
stati sono tutti vuoti e gli elettroni possono cambiare a piacimento il loro vettore d'onda sotto
l'azione del campo elettrico e delle collisioni all'interno del reticolo: il solido è un metallo. Infine,
se il minimo della banda di energia superiore è più basso del massimo della banda di energia
inferiore, anche in una diversa direzione dello spazio reciproco, gli elettroni si possono distribuire
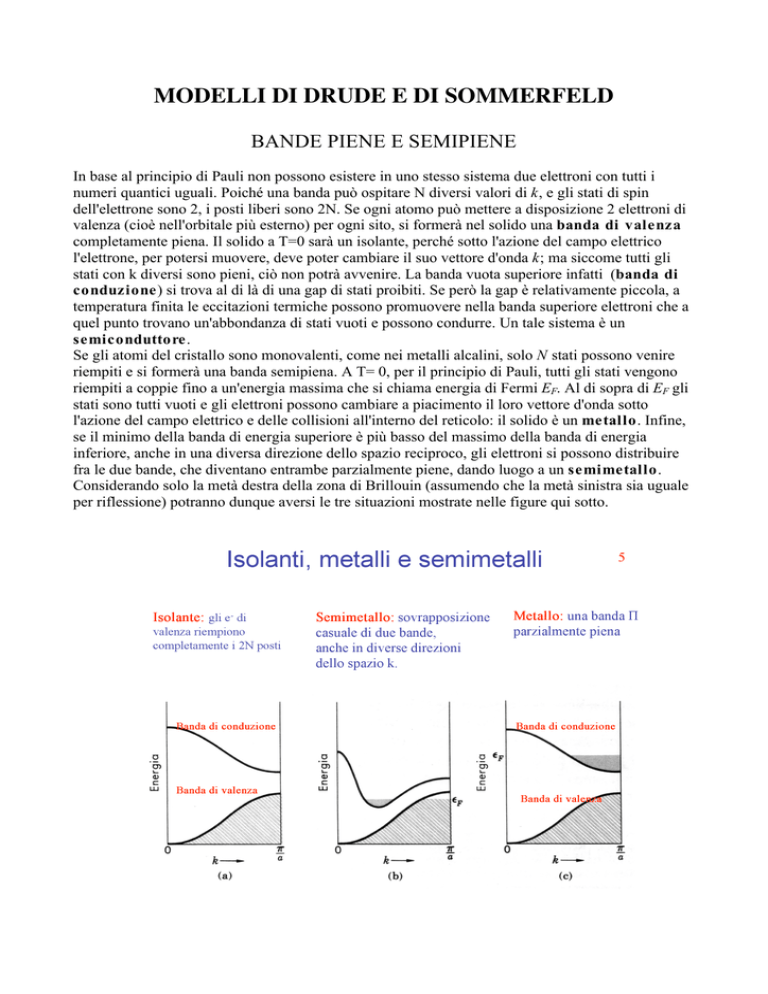
fra le due bande, che diventano entrambe parzialmente piene, dando luogo a un semimetallo.
Considerando solo la metà destra della zona di Brillouin (assumendo che la metà sinistra sia uguale
per riflessione) potranno dunque aversi le tre situazioni mostrate nelle figure qui sotto.
I METALLI IN UN CAMPO ELETTRICO
Il modello di Drude
€
Prima che fosse nota la meccanica quantistica e l'esistenza delle bande nei solidi, il trasporto della
corrente nei metalli veniva spiegato con un modello classico, il modello di Drude.
Nel modello di Drude le cariche positive (ioni) sono fisse e quelle negative sono completamente
r
libere
come in un gas perfetto. La velocità termica media è < v >= 0 ma il campo elettrico
r
r
E accelera gli elettroni a una velocità media di deriva < v deriva > finché dopo un tempo medio τ non
subiscono casualmente un urto con gli ioni in cui perdono memoria dello stato precedente (diremmo
che la funzione di autocorrelazione delle velocità si €
annulla dopo τ).
La forza è
r €dvr
r
−eE = m
= m v deriva / τ
dt
Se n è la densità di elettroni, la densità di corrente (carica totale che passa per una sezione di area
unitaria del conduttore nell’unità di tempo) è, se A è l’area della sezione del conduttore e
€ cariche che la possono attraversare nel tempo τ ,
V = A ⋅ v deriva τ il volume delle
€
r
r q −enA ⋅ v deriva τ
r
j=
=
= −en v
Aτ
Aτ
Per la legge di Ohm,
e quindi la conducibilità elettrica σ è
€
dove
€
deriva
−eτ r
= −en
E
€m
j =σE
σ = ne 2τ /m = neµ
µ=
eτ
m
è la mobilità degli elettroni. €
Conoscendo e, m e valutando n dalla densità del metallo d e il suo peso atomico dell’elemento A e
la sua valenza Z si ottiene la densità di elettroni
€
d
n= Z
A
Di qui, misurando la resistività del metallo
m
ρ= 2
ne τ
€
e ricavando n dal numero di elettroni di valenza e dalla densità del metallo, si ricava il tempo di
rilassamento o tempo medio fra urti τ che risulta dell’ordine di 10-14 o 10-15 s.
Drude immaginava c he gli elettroni€urtassero gli ioni del reticolo. Questo assunto però è sbagliato,
perché gli elettroni, essendo onde, si muovono imperturbati in un potenziale
periodico mentre possono essere scatterati solo dalle impurezze presenti nel cristallo e dai
fononi ((i quanti di vibrazione del reticolo, vedi Parte 4). Infatti, se fosse vero il modello di Drude,
la resistività sarebbe indipendente dalla temperatura mentre si osserva che cresce come T 5 a bassa T
e come T ad alta T (proprio a causa dell’aumento con T della densità dei fononi). L’accordo
qualitativo del modello di Drude con alcuni dati sperimentali derivava in realtà da una fortunata
eliminazione reciproca di errori.
La sfera di Fermi
Nel 1927 Sommerfeld modificò il modello di Drude per renderlo compatibile con la meccanica
quantistica e introdusse il concetto di densità degli stati. Successivamente, il modello fu
completato con l'introduzione della statistica di Fermi.
Come abbiamo visto, l'imposizione delle condizioni cicliche al contorno alla catena di N atomi
lunga L quantizza il vettore d'onda k. Entro l'intervallo 2π /a ci sono N stati; quindi c'è uno stato
possibile per l'elettrone ogni intervallo
2π 2π
€ =
aN
L
Perciò la densità degli stati k in una dimensione è
€
ρ(k) =
L
2π
€
In 2 dimensioni la distribuzione degli stati è presentata in Figura. Passando a 3 dimensioni, nella
zona di B. di un cristallo cubico semplice c'è uno stato k in un volumetto
 2π  3
 
L 
Supponiamo che anche il solido sia un cubo di volume V = L3 . Allora la densità degli stati
nello spazio k è
€
r
V
ρ( k ) =
(2π ) 3
€
Perciò, considerando anche lo spin, se N è il numero totale di elettroni disponibili, il massimo
vettore d'onda k F che in ogni direzione dello spazio isotropo k corrisponde a uno stato pieno a T =
€
0, è fissato dalla condizione
2 ⋅ (4 /3)πkF
€
3
V
V
3
= 2 kF = N
3
(2π )
3π
La sfera di raggio k F si chiama sfera di Fermi e la sua superficie, superficie di Fermi.
Naturalmente, in reticoli con simmetrie più complesse la superficie di Fermi può assumere forme
molto più complicate.
Di qui si ottiene per il vettore d'onda di Fermi
1
 3π 2 N  3
kF = 

 V 
e poiché l'energia di Fermi è
€
EF =
h2 2
kF
2m
si ricava
2
€
h 2  3π 2 N  3
EF =


2m  V 
Infine la velocità di Fermi, cioè la velocità di un elettrone che si muove sulla superficie di
Fermi, è
1
€
hkF h  3π 2 N  3
vF =
= 

m
m V 
Poiché gli elettroni eccitabili dal campo sono quelli che hanno velocità prossime a v F, il cammino
libero medio degli elettroni fra un urto e l’altro è
€
λ ≈ vFτ
Dall’espressione di EF possiamo anche ricavare il numero N degli stati che si trovano al di sotto di
una generica energia E
€
3
V  2mE  2
N = 2 2 
3π  h 
e quindi la densità degli stati per unità di energia
€
3
1
dN
V  2m  2 2
ρ(E) =
=
  E
dE 2π 2  h 2 
Come è noto, a temperature T > 0 la probabilità di occupazione di uno stato fermionico è data
dalla funzione di Fermi
€
1
f (T) =
 E − µ
exp
 +1
 kB T 
€
dove è il potenziale chimico. A E = la probabilità di occupazione è 1/2 a ogni T. Allo zero
assoluto coincide con l'energia di Fermi. Infatti a T =0 f (T) è una funzione gradino con la
discontinuità a . I grafici mostrano l'andamento di f (T) (curva rossa) a diverse temperature per una
energia di Fermi di 5 eV.
€
€
Per gli elettroni di un metallo in banda semipiena, la conducibilità si può ancora calcolare con il
modello di Drude, solo che ora l'effetto del campo elettrico per un tempo t si può vedere nello
spazio k: a spostarsi di una quantità δk = −eEt /h è l'intera sfera di Fermi, come mostra la Figura qui
sotto.
€
In condizioni stazionarie, quando gli elettroni fluiscono con una velocità di deriva
< v deriva >= −eEτ /m, δk = −eEτ /h .
€
IL CALORE SPECIFICO NEI METALLI: IL CONTRIBUTO
DEGLI ELETTRONI DI CONDUZIONE
Come sempre, sia
c v (T) =
∂U
(erg /g ⋅ K)
∂T
il calore specifico a volume costante (ovvero capacità termica per unità di massa). A
differenza degli isolanti, nei metalli è presente, oltre al contributo dei fononi del
reticolo, quello degli elettroni
di conduzione c v el .
€
Alla temperatura T, l’energia totale del gas di elettroni è
U=
•
∫ ε g(ε) f (ε)dε
0
€
dove
g(ε) è la densità degli stati e f (ε,T) =
è il potenziale chimico (che coincide
con EF a T=0).
€ Nel modello di
Sommerfeld (elettroni non interagenti)
per T<< TF (TF ≈103÷104 K), viene
sviluppato in serie di potenze pari di T
(i termini dispari si annullano).
In questo modo, al primo ordine, anche
l'energia cinetica degli elettroni per
unità di volume ha una forma
quadratica
U(T)
π2
u(T) =
≈ u(0) +
(k B T) 2 ρ(E F )
V
6V
come confermano misure ottiche come
quella in Figura.
€
In figura: Peso spettrale,
W (T) =
Ω
∫ σ (ω )dω ∝ u(T)
0
€
(dove σ è la conducibilità ottica e  è una
frequenza di taglio) lineare con T2 per diverse
 in oro e in due superconduttori ad alta Tc
con diverso drogaggio
[Ortolani, Calvani, Lupi, Phys. Rev. Lett.
2005.]
1
e
(ε − µ )/ kB T
+1
Per elettroni liberi in 3D,
3
1
dN
V  2m  2
ρ(E) =
= 2 2  E2
dE 2π  h 
dove è inclusa la degenerazione di spin. E poiché
2
€
h 2  3π 2 N  3
EF =


2m  V 
€
Sostituendo,
€
ρ(E F ) =
3 N 3 nV
=
2 EF 2 EF
u(T) ≅ u(0) +
π2
n
(k B T) 2
4
EF
Derivando rispetto a T si ricava il calore specifico elettronico per unità
di volume
€
 ∂u(T)  π 2  k B T 
3
c ′el v (T) = 
 = 
 nk (erg /cm K)
 ∂T  v 2  E F  B
Il calore specifico totale di un metallo monoatomico (natomi = nelettroni), per
unità di volume, è quindi
€
3


12π 4  T  π 2  k B T 

c ′v (T) = nk B
  + 

2  E F 
 5  TD 
dove TD è la temperatura di Debye. Da esso, moltiplicando per la densità
del solido, si€ottiene c v (T) .
Come si vede, il contributo degli elettroni di conduzione a T<<TF è
lineare con T, mentre quello degli ioni a bassa temperatura è
3
proporzionale
€aT.
La causa di questo effetto sta nel fatto che, mentre i fononi seguono la
distribuzione di Bose-Einstein, che consente eccitazioni di energia
qualunque, gli elettroni seguono quella di Fermi-Dirac che, per il
principio di esclusione di Pauli, consente l'eccitazione solo verso uno
stato vuoto. Di conseguenza soltanto gli elettroni che si trovano in un
sottile strato di spessore kBT intorno a EF possono assorbire un'energia
kBT, perché al di sopra di essi tutti gli
stati sono vuoti:
Sfera di
Fermi
E F − kB T
EF
In formule, partendo dalla situazione a T=0 e riscaldando il metallo, ciò
significa che la variazione di energia cinetica degli elettroni sarà
dell'ordine di
€
∆u0 (T) = u0 (T) − u0 (T = 0) ≈ Stati di partenza possibili × Energia assorbita = ρ(E F )kB T ⋅ k B T =
= ρ(E F )(k B T) 2 µ (1/ E F )(k B T) 2
€
Di qui, dividendo per ∆T = T , si ritrova
c el =
€
€
∆U ∆U k 2 B
=
µ
T
∆T
T
EF