STATISTICA PSICOMETRICA a.a. 2004/2005
Corsi di laurea
Scienze e tecniche neuropsicologiche
Modulo 1
Statistica descrittiva Monovariata
1
Modulo 1
Statistica descrittiva Monovariata
•Distribuzioni semplici di frequenza e loro rappresentazioni
•Operatori di tendenza centrale
•Operatori di dispersione
•Momenti omogenei ed indici di forma (simmetria/curtosi
(simmetria/curtosi))
•Standardizzazione di variabili cardinali
2
1
Statistica descrittiva Monovariata
Distribuzioni semplici di frequenza e loro rappresentazioni
Dalla distribuzione unitaria
alla distribuzione semplice di frequenze
ident
1
2
3
4
5
6
7
8
9
10
11
12
13
genere
1
2
1
1
2
1
1
2
1
2
1
1
2
(sconnessa,ordinata,seriazione)
Matrice CxV:
tante righe quanti
sono i casi (N) !
genere
n
1
2
8
5
Distribuzione di
frequenza : tante
righe quante sono le
modalità della
variabile (K) ! 3
Statistica descrittiva Monovariata
Distribuzioni semplici di frequenza e loro rappresentazioni
Frequenze:
Assolute
nk
K
∑n
k =1
Relative
n
fk = k
N
k
K
∑f
k =1
K
Percentuali
qk = f k • 100
∑q
k =1
k
k
=N
=1
= 100
4
2
Statistica descrittiva Monovariata
Distribuzioni semplici di frequenza e loro rappresentazioni
ident
1
2
3
4
5
6
7
8
9
10
11
12
13
residenza
1
2
1
1
2
3
4
2
1
3
4
3
1
residenza
1
2
3
4
totale
n
f
q
5
3
3
2
0,38
0,23
0,23
0,15
38,5
23,1
23,1
15,4
13
1
100
5
Statistica descrittiva Monovariata
Distribuzioni semplici di frequenza e loro rappresentazioni
Se la variabile è ordinale parliamo di serie ordinata di
frequenze Î posso calcolare le frequenze cumulate
ident
1
2
3
4
5
6
7
8
9
10
11
12
13
titolo di
studio
1
2
1
2
3
2
1
2
3
3
2
1
2
titolo di
studio
1=obbligo
2=med. Sup.
3=laurea
n
4
6
3
f
0,31
0,46
0,23
q
30,8
46,2
23,1
n'
f'
4
10
13
0,31
0,77
1,00
q'
30,8
76,9
100,0
… quanti soggetti hanno al massimo …?
6
3
Statistica descrittiva Monovariata
Distribuzioni semplici di frequenza e loro rappresentazioni
Rappresentazioni Grafiche
n
sud
15%
Serie sconnessa
Îdiagramma a torta (o a barre)
nord
39%
isole
23%
centro
23%
50,0
Serie ordinata
Îistogramma
46,2
45,0
40,0
35,0
30,8
30,0
23,1
25,0
20,0
15,0
10,0
5,0
0,0
1=obbligo
2=med. Sup.
3=laurea
7
Statistica descrittiva Monovariata
Operatori monovariati
Un operatore statistico monovariato è:
un procedimento di calcolo che produce una statistica con
le seguenti caratteristiche
1. È costituita da un unico scalare
2. Si riferisce ad una singola variabile
3. È appropriata al livello di scala
4. È insensibile all’ordine in cui i dati vengono registrati
8
4
Statistica descrittiva Monovariata
Operatori monovariati
Un operatore statistico monovariato può essere
1. Un operatore di tendenza centrale (il valore che rappresenta al
meglio la distribuzione intera)
2. Un operatore di dispersione (il valore che informa circa la
diversità esistente tra le osservazioni)
3. Un operatore di forma (relativi alla simmetria o alla curtosi della
distribuzione)
9
Statistica descrittiva Monovariata
Operatori di tendenza centrale
Î Moda
Î Mediana
Î Media
10
5
Statistica descrittiva Monovariata
Operatori di tendenza centrale: Moda
Moda= modalità della variabile con frequenza più elevata
Idonea per scale nominali, ordinali e cardinali
moda
residenza
nord
centro
isole
sud
n
5
3
3
2
La moda è “Nord” , perché è la modalità della variabile RESIDENZA che
si presenta con la frequenza più elevata (n=5)
11
Statistica descrittiva Monovariata
Operatori di tendenza centrale: Mediana
Mediana= modalità a cui appartiene il caso (caso mediano)
che divide esattamente in due la distribuzione
Idonea per scale ordinali e cardinali
Se N (numero totale dei casi) è dispari il caso mediano sarà
uno solo
C Mdn =
( N + 1)
2
Se N (numero totale dei casi) è pari avremo due casi mediani
1°C Mdn =
N
2
2°C Mdn =
N
+1
2
12
6
Statistica descrittiva Monovariata
Operatori di tendenza centrale: Mediana
I casi sono dispari (13) quindi c’è solo un caso mediamo
C Mdn
( N + 1)
=
2
C Mdn =
titolo di
studio
1=obbligo
2=med. Sup.
3=laurea
n
4
6
3
(13 + 1) 14
=
=7
2
2
f
0,31
0,46
0,23
q
30,8
46,2
23,1
n'
4
10
13
Calcolando le frequenze cumulate vediamo che il 7° caso
cade nella categoria Media superiore.
Media superiore rappresenta quindi la mediana della
distribuzione
13
Statistica descrittiva Monovariata
Operatori di tendenza centrale: Media Aritmetica
Media (aritmetica): la media si ottiene sommando tutti i valori
di X (da 1 a N) e dividendo tale somma per il numero dei
casi (N)
Idonea per scale cardinali
1
x=
N
N
∑x
i =1
i
14
7
Statistica descrittiva Monovariata
Operatori di tendenza centrale: Media Aritmetica
ident
peso
1
2
3
4
5
x=
1
x=
N
72
58
65
78
49
N
∑x
i =1
i
(72 + 58 + 65 + 78 + 49) 322
=
= 64,4
5
5
15
Statistica descrittiva Monovariata
Operatori di tendenza centrale: Media Aritmetica
Proprietà della media
Î La somma algebrica degli scarti dei valori dalla loro media
aritmetica è uguale a zero
N
∑ ( x − x) = 0
i =1
ident
i
peso
1
2
3
4
5
scarto
72
58
65
78
49
somma
7,6
-6,4
0,6
13,6
-15,4
0,0
16
8
Statistica descrittiva Monovariata
Operatori di tendenza centrale: Media Aritmetica
Proprietà della media
Î La somma algebrica dei quadrati degli scarti dei valori
dalla loro media aritmetica è minima
N
∑ ( x − a)
i =1
i
2
= min
se
a=x
17
Statistica descrittiva Monovariata
Operatori di tendenza centrale: Altri indici di posizione
Così come la mediana è la modalità nella quale cade il caso
che divide in 2 parti uguali la distribuzione possiamo
pensare ad indici che dividono in più parti uguali la
distribuzione
Ad esempio i quartili sono le categorie nelle quali cadono i 3
casi che dividono in 4 parti uguali la distribuzione
Idonea per scale ordinali e cardinali
Quartili – decili – centili
quantili
18
9
Statistica descrittiva Monovariata
Operatori di dispersione
Î Mutabilità Categoriale
Î Varibilità non metrica Ordinale
Î Variabilità metrica Cardinale
19
Statistica descrittiva Monovariata
Operatori di dispersione
Un operatore di dispersione produce uno scalare con cui si
valuta sinteticamente la diversità esistente tra le osservazioni
ID
Campione 1
età
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
ID
27
25
32
27
25
27
31
30
32
27
26
26
33
30
25
33
27
34
30
26
età
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
45
34
67
34
25
18
17
6
21
8
24
39
41
15
26
45
10
24
63
11
Campione 2
20
10
Statistica descrittiva Monovariata
Operatori di dispersione
I due campione hanno media identica
ID
età
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
ID
27
25
32
27
25
27
31
30
32
27
26
26
33
30
25
33
27
34
30
26
Media
Campione 1
età
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
21
20
Media
Campione 2
28,65
45
34
67
34
25
18
17
6
21
8
24
39
41
15
26
45
10
24
63
11
Statistica descrittiva Monovariata
Operatori di dispersione
Sono molto diversi invece per quanto riguarda il campo di
variazione
ID
età
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
ID
27
25
32
27
25
27
31
30
32
27
26
26
33
30
25
33
27
34
30
26
25
Campione 1
34
Campione 2
6
67
età
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
22
20
45
34
67
34
25
18
17
6
21
8
24
39
41
15
26
45
10
24
63
11
11
Statistica descrittiva Monovariata
Operatori di dispersione: mutabilità
Per variabili categoriali
Eterogeneità
Omogeneità
Ciascuna modalità
della variabile ha la
medesima frequenza
(N/K)
Capitale preferita
Parigi
Londra
Berlino
Madrid
Praga
Tutte le osservazioni
si riferiscono ad una
sola modalità
Capitale preferita
n
n
Parigi
Londra
Berlino
Madrid
Praga
20
20
20
20
20
0
100
0
0
0
23
Statistica descrittiva Monovariata
Operatori di dispersione: mutabilità
Indice di GINI
Uno meno la sommatoria per k che va da 1 a K del quadrato
delle frequenze relative
K
E1 = 1 − ∑ f k2
k =1
(K-1)/K
Eterogeneità
0
Omogeneità
24
12
Statistica descrittiva Monovariata
Operatori di dispersione: mutabilità
Indice di GINI: esempio
Capitale
preferita
Parigi
Londra
Berlino
Madrid
Praga
n
f2
f
21
18
35
11
15
0,21
0,18
0,35
0,11
0,15
somma=
E1
Praga
15%
0,044
0,032
0,123
0,012
0,023
Capitale preferita
Parigi
Londra
Berlino
Madrid
Praga
n
7
11
15
16
51
0,234
0,766
f2
f
0,07
0,11
0,15
0,16
0,51
0,325
0,675
somma=
E1
Parigi
21%
Parigi
7%
0,005
0,012
0,023
0,026
0,26
Londra
11%
Madrid
11%
Londra
18%
Berlino
15%
Praga
51%
Madrid
16%
Berlino
35%
25
Statistica descrittiva Monovariata
Operatori di dispersione: mutabilità
Indici relativi
Tramite l’operazione di ranging possiamo far variare l’indice
di GINI tra 0 ed 1
Le misure relative (e) si ottengono sottraendo a quelle
assolute (E) il valore minimo che possono raggiungere e
dividendo il risultato per il suo intervallo di variazione
E − min
e=
max − min
26
13
Statistica descrittiva Monovariata
Operatori di dispersione: mutabilità
Indici relativi
Nel caso dell’indice di GINI
e1 =
E1 − 0
E1
K
=
=
E
( K − 1)
( K − 1) K − 1 1
−0
K
K
27
Statistica descrittiva Monovariata
Operatori di dispersione: mutabilità
Altri indici
Nome
Gini
Formula
K
E1 = 1 − ∑ f k2
min
0
k =1
Leti
max
K −1
K
1
E3 =
K
f
∏ fk k
1
K
0
log a K
k =1
Entropia
K
E2 = 1 − ∑ f k log a f k
k =1
28
14
Statistica descrittiva Monovariata
Operatori di dispersione: variabilità non metrica
Per variabili ordinali
In una variabile ordinale è ragionevole considerare come più
simili le osservazioni che cadono in modalità contigue,
piuttosto che osservazioni che cadono in modalità estreme.
L’operatore D* gode di queste proprietà
K −1
[ (
D = 2∑ f k' 1 − f k'
*
)]
k =1
Valore minimo =0
K −1
1
1− 2
Se N è dispari
2 N
Valore massimo =
K −1
2
Se N è pari
29
Statistica descrittiva Monovariata
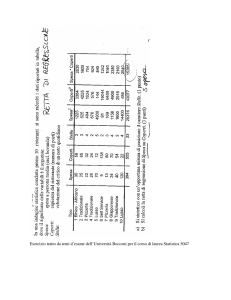
Operatori di dispersione: variabilità non metrica
Per variabili ordinali
Titolo di studio
Elementari
Media inferiore
Media Superiore
Laurea
f
0,3
0,2
0,2
0,3
K −1
[ (
f'
0,3
0,5
0,7
1
D = 2∑ f k' 1 − f k'
*
1-f' f' (1-f' )
0,7 0,21
0,5 0,25
0,3 0,21
0
)]
k =1
D * = 2(0,21 + 0,25 + 0,21) = 2(0,67) = 1,34
30
15
Statistica descrittiva Monovariata
Operatori di dispersione: variabilità metrica
Per variabili cardinali
Prendiamo in considerazione due famiglie di operatori
• intervalli di variazione
•Scarti da un valore centrale
31
Statistica descrittiva Monovariata
Operatori di dispersione: variabilità metrica
Gli intervalli di variazione sono operatori che quantificano la
variabilità misurando la diversità tra due particolari termini
della distribuzione
RANGE
W = Xmax – Xmin
SEMIDIFFERENZA INTERQUARTILE
W’ = Q3 – Q1
32
16
Statistica descrittiva Monovariata
Operatori di dispersione: variabilità metrica
Scarti da un valore centrale
(
N
Devianza
DEV = ∑ xi − x
Varianza
∑ (x − x )
)
2
i =1
2
N
S =
2
i
i =1
N
∑ (x − x )
2
N
Deviazione Standard
S =
Coefficiente di variazione
i
i =1
N
cv =
s
⋅100
x 33
Statistica descrittiva Monovariata
Operatori di dispersione: variabilità metrica
Esempio:range
Campione 1
ID
età
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
27
25
32
27
25
27
31
30
32
27
26
26
33
30
25
33
27
34
30
26
ID
W=34-25=9
W=67-6=61
età
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
45
34
67
34
25
18
17
6
21
8
24
39
41
15
26
45
10
24
63
11
Campione 2
34
17
Statistica descrittiva Monovariata
Operatori di dispersione: variabilità metrica
Esempio.devianza
Campione 1
ID
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
media=
età
scarti
27
-1,65
25
-3,65
32
3,35
27
-1,65
25
-3,65
27
-1,65
31
2,35
30
1,35
32
3,35
27
-1,65
26
-2,65
26
-2,65
33
4,35
30
1,35
25
-3,65
33
4,35
27
-1,65
34
5,35
30
1,35
26
-2,65
28,65 DEV=
2
scarti
2,723
13,323
11,223
2,723
13,323
2,723
5,523
1,823
11,223
2,723
7,022
7,022
18,923
1,823
13,323
18,923
2,723
28,623
1,823
7,022
N
(
DEV = ∑ xi − x
i =1
)
2
35
174,550
Statistica descrittiva Monovariata
Operatori di dispersione: variabilità metrica
Esempio.devianza
Campione 2
ID
età
1
45
2
34
3
67
4
34
5
25
6
18
7
17
8
6
9
21
10
8
11
24
12
39
13
41
14
15
15
26
16
45
17
10
18
24
19
63
20
11
scarti
16,35
5,35
38,35
5,35
-3,65
-10,65
-11,65
-22,65
-7,65
-20,65
-4,65
10,35
12,35
-13,65
-2,65
16,35
-18,65
-4,65
34,35
-17,65
media= 28,65 DEV=
scarti2
267,32
28,62
1470,72
28,62
13,32
113,42
135,72
513,02
58,52
426,42
21,62
107,12
152,52
186,32
7,02
267,32
347,82
21,62
1179,92
311,52
5658,55
N
(
DEV = ∑ xi − x
i =1
)
2
36
18
Statistica descrittiva Monovariata
Operatori di dispersione: variabilità metrica
Esempio: varianza , deviazione standard, coefficiente var.
(
N
DEV = ∑ xi − x
Devianza
i =1
∑ (x
N
Varianza
S2 =
Deviazione
standard
i =1
i
)
2
−x
Coefficiente di
variazione
Campione
2
174,6
5658,6
8,73
282,93
2,95
16,82
10,31
58,71
N
∑ (x − x )
2
N
S =
)
2
Campione
1
i =1
i
N
s
cv = ⋅100
x
37
Statistica descrittiva Monovariata
Momenti omogenei ed indici di forma
Momento omogeneo= media dei valori di una variabile presa
con esponente positivo
r = ordine del momento
r
N
M=
∑ (x )
i
i =1
N
∑ (x − x )
r
N
M =
i =1
i
N
Momento non centrale
Momento centrale
non è uno scarto dalla media
è uno scarto dalla media
38
19
Statistica descrittiva Monovariata
Momenti omogenei ed indici di forma
Ordine
tipo
Informazione
1
non centrale
Esempio
3
centrale
tendenza centrale
della distribuzione
dispersione della
distribuzione
Asimmetria
4
centrale
Curtosi
centrale
2
1
N
x=
S2 =
1
N
N
∑x
i
i =1
∑ (x
N
i =1
i
)
2
−x
β1
β2
39
Statistica descrittiva Monovariata
Momenti omogenei ed indici di forma
β1
Asimmetria
positiva
Asimmetria
negativa
-
0
+
x = mdn = mod
x < mdn < mod
x > mdn > mod
40
20
Statistica descrittiva Monovariata
Momenti omogenei ed indici di forma
Leptocurtica
Platicurtica
β2
-
0
+
41
Statistica descrittiva Monovariata
Standardizzazione di una variabile cardianle
Dispositivo per rendere confrontabili distribuzioni diverse.
Le distribuzioni vengono trasformate in distribuzioni con
media =0 e deviazione standard=1
Centratura
Varaibile X
Scarti dalla media
Uniformazione
Punti Z
Divisione per s
42
21
Statistica descrittiva Monovariata
Standardizzazione di una variabile cardianle
Dispositivo per rendere confrontabili distribuzioni diverse.
Le distribuzioni vengono trasformate in distribuzioni con
media =0 e deviazione standard=1
zi
(
x − x)
=
i
s
43
Statistica descrittiva Monovariata
Standardizzazione di una variabile cardianle
zi =
ident
1
2
3
4
5
media
s
(x − x )
i
s
altezza
peso
1,72
1,65
1,81
1,75
1,82
1,75
0,062
72
65
93
61
73
alezza z peso z
-0,48
-0,07
-1,61
-0,71
0,96
1,83
0,00
-1,07
1,12
0,02
72,8
11,034
44
22