CAPITOLO I,
ELETTROSTATICA NEL VUOTO
I) LA CARICA ELETTRICA E LA LEGGE DI COULOMB
OSSERVAZIONE SPERIMENTALE,
PROPRIETA’ DELLA CARICA ELETTRICA.
1)Esistono due tipi di carica: la carica positiva e la carica negativa. Cariche di uguale segno si
respingono, cariche di segno opposto si attraggono.
2)La carica è conservativa. Questo significa che la carica di un sistema isolato si conserva.
3)La carica è quantizzata. Esiste infatti una quantità minima di carica che non può essere frazionata,
per cui ogni carica è multiplo intero di tale quantità. La carica più piccola è quella dell’elettrone
che, nel sistema internazionale, vale e 1,6 10 19 .
OSSERVAZIONE SPERIMENTALE,
LA LEGGE DI COULOMB. Nel vuoto la forza che la carica puntiforme q1 esercita sulla carica
puntiforme q2 è data da
F 0 r 2 K 0
r 2 r1
r 2 r1
q1 q 2
2
r 2 r1
dove
K 0 9 10 9
N m2
C2
I valori di q1 e q2 si intendono come valori algebrici. Essi possono dunque essere positivi o negativi.
DEFINIZIONE,
IL COULOMB. Nel sistema internazionale il coulomb è un’unità derivata (l’unità elettrica
fondamentale è infatti l’ampere). Esso è definito come la carica che ciascuna di due cariche uguali
possiede quando la forza con cui esse si respingono, alla distanza di un metro, ha modulo
F 9 10 9 N .
DEFINIZIONE,
COSTANTE DIELETTRICA DEL VUOTO. Per ragioni formali si pone
K0
1
4 0
0 8.85 10 12
C2
Nm 2
e la costante 0 prende il nome di costante dielettrica del vuoto.
DEDUZIONE,
FORZE COULOMBIANE PER UNA DISTRIBUZIONE DI CARICHE. Consideriamo n
cariche puntiformi. La forza coulombiana da esse esercitata su una carica q posta nel generico punto
dello spazio è data da
1
q
F0 r
4 0
n
i 1
r ri
qi
2
r ri
r ri
Consideriamo ora una carica distribuita con densità ρ in un volume Ω. In tal caso la forza
coulombiana agente sulla carica q è data da
q
F0 r 2
40
r 2 r1
r 2 r1
2
dV
r 2 r1
II) IL CAMPO ELETTRICO
DEFINIZIONE,
CAMPO ELETTRICO. Definiamo campo elettrico nel vuoto relativo alla carica q il campo
vettoriale E 0 che fornisce il rapporto tra la forza, nel punto P, che la carica q esercita su una carica
q ' posta in P, e il valore della stessa q ' .
DEDUZIONE,
ESPRESSIONE DEL CAMPO ELETTRICO NEL VUOTO. In base alla sua definizione
l’espressione del campo elettrico nel vuoto relativo alla carica q è fornita da
1 q r
E 0 r
4 0 r 2 r
dove si assume che la carica sia nell’origine del sistema di riferimento e che r sia il vettore che
conginge l’origine del sistema di riferimento con il punto nel quale si calcola il campo elettrico.
2
OSSERVAZIONE,
UNITA’ DI MISURA DEL CAMPO ELETTRICO NEL VUOTO. Il campo elettrico nel vuoto
si esprime in
newton
coulomb
metro
massa metro
sec ondo 2
.
coulomb
coulomb sec ondo 2
massa
DEDUZIONE,
CAMPO ELETTRICO DI UNA DISTRIBUZIONE DI CARICHE. Consideriamo n cariche
puntiformi. Il campo elettrico da esse prodotto nello spazio è dato da
1
E 0 r
4 0
n
1
r ri
qi
2
r ri
r ri
Consideriamo ora una carica distribuita con densità ρ in un volume Ω. In tal caso il campo elettrico
è dato da
E 0 r 2
4 0
1
r 2 r1
r 2 r1
2
dV
r 2 r1
III) LA LEGGE DI GAUSS
DEDUZIONE,
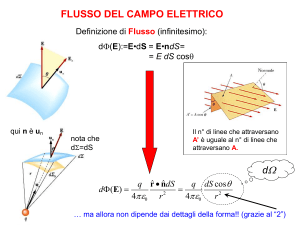
LEGGE DI GAUSS. Una carica puntiforme nel vuoto q sia posta all’interno di una generica
superficie chiusa Ψ. Allora il flusso del campo elettrico attraverso Ψ è dato da
E 0 dS
q
0
.
DIMOSTRAZIONE. Calcoliamo il flusso del campo elettrico attraverso la superficie chiusa Ψ. A
tale scopo indichiamo la generica rappresentazione parametrica di una superficie chiusa in
coordinate sferiche.
x r , sin cos
y r , sin sin
z r , cos
, D , 2 | 0, , 0,2
Il flusso di E 0 attraverso Ψ è dato da
3
A2 B 2 C 2
dS
A, B, C
q r sin cos r sin sin r cos
, 3
,
4 0 r 3 ,
r , r 3 ,
D
A, B, C
E 0 dS E 0
q
4 0
A B C
2
2
2
A 2 B 2 C 2 dd
sin cos
sin sin
cos
A , 2
B , 2
C , dd
2
r ,
r ,
r ,
D
Dove A, B, C sono definite dalla relazione
x y z x y z
,
,
,
,
A, B, C
y
z
r r sen r r sen cos cos r 2 sen 2 cos
z
z
B ,
z
x
r
r
2
2
x r sen cos sin r cos r sen sen
x
C ,
x
y
A ,
y
r r sen 2 r 2 sen cos
y
In base a ciò il flusso si scrive
E 0 dS
q
40
q
4 0
q
0
sin cos
sin sin
cos
A , 2
B , 2
C , dd
2
r ,
r ,
r ,
D
2
q
q
2
0
0
sin dd 4 sin dd 4 cos
D
0
0 0
0
d
q
4 0
2
q
2d 4
0
4
0
.
Con ciò la tesi è dimostrata.
DEDUZIONE,
PRIMA EQUAZIONE DI MAXWELL NEL VUOTO. La divergenza del campo elettrico nel
vuoto è data da
4
div E 0
0
DIMOSTRAZIONE. In base alla legge di Gauss si ha
dV
0
E0 dS
Per il teorema della divergenza si ha
E0 dS div E0 dV
Da queste due relazioni si ottiene, per confronto, che
dV
0
div E0 dV
Poiché questa relazione continua ad essere valida comunque si scelga un sottodominio di Ω, ne
segue che l’uguaglianza fra i due termini integrandi. E dunque la tesi.
DEDUZIONE,
CAMPO ELETTRICO DELLO STRATO PIANO. Si immagini di avere una carica distribuita
con densità uniforme σ su una superficie piana di estensione infinita. Questa distribuzione è detta
strato piano. Calcoliamo il campo elettrico da essa generato nello spazio sfruttando la legge di
Gauss.
Si consideri la superficie cilindirca in figura. Il flusso del campo elettrico generato dalla porzione di
carica da essa racchiusa vale
cilindro E E 0 dS E 0 dS 2 E 0 dS
cilindro
mantello
base
Ora osserviamo che le componenti del campo elettrico, prodotte da
ogni elemento dello strato piano, parallele allo strato piano stesso si
annullano fra loro. Dunque il campo elettrico dello strato piano è, punto
per punto, ortogonale ad esso. Ne segue che il nostro flusso diviene
cilindro E E 0 dS 2 E 0 dS 2 E 0 S
cilindro
base
Ma per la legge di Gauss tale flusso deve essere pari a
2 E0 S
S
0
E0
S
0
. Dunque si ha
2 0
5
DEDUZIONE,
CAMPO ELETTRICO DEL DOPPIO STRATO PIANO.
Consideriamo due strati piani paralleli di densità di carica
uguale in modulo ma di segno opposto. Ebbene il campo
elettrico vale
nello spazio compreso fra i due strati ed è
0
nullo nel resto dello spazio. La sua direzione è ortogonale ai
due piani ed il suo verso è quello che dallo strato con carica
positiva va a quello con carica negativa.
DEDUZIONE,
IL CAMPO ELETTRICO NEL VUOTO E’ UN CAMPO CONSERVATIVO. Ricordiamo che
un campo vettoriale risulta conservativo se e solo se la forma differenziale ad esso associata risulta
esatta.
Scriviamo dunque il campo elettrico nel vuoto rispetto ad un sistema di coordinate cartesiane avente
l’origine coincidente con la posizione della carica q. Si ha
E0
1
40
q x i y j z k
x
y 2 z 2 2
3
2
dove si è posto r x i y j z k .
La forma differenziale ad esso associata è allora
E0
q
xdx ydy zdz .
40 r 3
1
Per verificarne l’esattezza è sufficiente indicarne una primitiva, per definizione stessa di forma
differenziale esatta. Ebbene la funzione
f
1
40
q
x
y 2 z 2 2
1
2
risulta essere tale. Infatti
f
1
x 40
f
1
y 40
f
1
z 40
qx
x
y 2 z 2 2
3
2
qy
x
y 2 z 2 2
3
2
y 2 z 2 2
3
2
E0 y ,
qz
x
E0 x ,
E0 z .
6
OSSERVAZIONE,
IL CAMPO ELETTRICO NEL VUOTO E’ UN CAMPO IRROTAZIONALE. Dire che un
campo è irrotazionale1 equivale a dire che un campo è conservativo. Dunque, in base alla deduzione
I.2, il campo E 0 è irrotazionale.
Verifichiamolo tuttavia direttamente a scopo di ripasso sull’operatore rotore. Lo faremo nei due
modi seguenti:
1)calcolando direttamente il rotore del campo E 0 ;
2)utilizzando il teorema di Stokes.
1)Il rotore di E 0 è dato da
i
rot E 0 , , E 0 E 0
x
x y z
E0 x
E 0 y
E
0 z
z
y
j
y
E0 y
k
z
E0 z
E 0 x E 0 z E 0 y E 0 x
i
j
x x
y
z
k .
In base al teorema di Schwartz ciascuna delle componenti di questo campo vettoriale è
evidentemente nulla.
2)Presa una curva chiusa γ, dalla conservatività del campo E 0 deriva che
E 0 T ds 0.
Dove T è il versore tangente della curva γ.
Ma per il teorema di Stokes si ha pure che
E 0 T ds rot E 0 dS.
S
Dove S è una qualunque superficie avente come bordo la curva γ. E dove è il campo del versore
normale alla superficie S stessa.
Ciò posto si ha
rot E 0 dS 0S rot E 0 0.
S
Che è quanto si voleva provare.
DEFINIZIONE,
SECONDA EQUAZIONE DI MAXWELL NEI CASI STAZIONARI. Si definisce ‘seconda
equazione di Maxwell nei casi stazionari’ l’equazione
1
Un campo si dice irrotazionale quando il suo rotore è nullo.
7
rot E 0 0
Essa si trova espressa anche nella forma equivalente
rot E
ds 0S
0
S
Verbalmente tale equazione si traduce nella affermazione
‘il campo elettrico nel vuoto è un campo conservativo cioè irrotazionale.’
IV) IL POTENZIALE ELETTROSTATICO
DEDUZIONE,
LAVORO DELLE FORZE ELETTRICHE. Il lavoro che le forze del campo prodotto da una
carica q realizzano per portare una carica q ' da una posizione ra ad una posizione rb è fornito dalla
espressione
Lab
1 1
qq '
40
ra rb
1
DIMOSTRAZIONE. Si consideri la curva
x x t
y y t
z z t
t a , b
La carica q sia all’origine del sistema di riferimento. La carica q ' sia invece posta nella posizione
γ(a), individuata dal vettore ra . Calcoliamo il lavoro che le forze del campo debbono fare per
portare la carica nella posizione γ(b), individuata dal vettore rb . Si ha
Lab F T ds q ' E0 T ds
1
40
q ' q x i y j z k
T ds
x
y 2 z 2 2
3
2
x t x t y t y (t ) z t z t
b
'
q'q
dt q q
3
4 0 a
4 0
2
2
2 2
x t y t z t
b
d
dt
a
1
xt
2
y t z t
2
1
2 2
8
b
'
qq
4 0
q'q
4 0
1
xt
2
y t z t
2
1 1 q'q
ra rb 4 0
1
2 2
a
q'q
1
4 0
2
2
2
x a y a z a
xb
1
2
1
2
y b z b
2
1
2 2
1 1
rb ra
DEFINIZIONE,
POTENZIALE ELETTROSTATICO NEL VUOTO. Definisco potenziale elettrostatico nel
vuoto relativo ad una carica puntiforme q il rapporto tra il lavoro che occorre fare contro le forze del
campo per portare una carica puntiforme q ' da una posizione di infinita distanza da q alla posizione
di q, e la carica q ' stessa.
DEDUZIONE,
ESPRESSIONE DEL POTENZIALE ELETTROSTATICO NEL VUOTO. In base alla sua
definizione risulta che il potenziale elettrico nel vuoto relativo alla carica puntiforme q è dato dalla
funzione di punto
V 0 P
1
q
4 0 r P
OSSERVAZIONE,
UNITA’ DI MISURA DEL POTENZIALE ELETTRICO NEL VUOTO. Il potenziale elettrico
nel vuoto si misura in
volt
newton m
coulomb
DEFINIZIONE,
IL VOLT. Definisco volt il seguente rapporto di unità di misura:
volt
newton m
coulomb
DEDUZIONE,
POTENZIALE ELETTROSTATICO DI UNA DISTRIBUZIONE DI
Consideriamo n cariche puntiformi. Il potenziale elettrico ad esse relativo è dato da
1
V0 r
4 0
n
1
CARICHE.
qi
r ri
Consideriamo ora una carica distribuita con densità ρ in un volume Ω. In tal caso il potenziale è
dato da
9
r 1
1
V0 r 2
4 0
dV
r 2 r1
DEDUZIONE,
RELAZIONE FRA POTENZIALE ELETTROSTATICO NEL VUOTO E CAMPO
ELETTRICO NEL VUOTO PER UNA CARICA PUNTIFORME. Consideriamo una carica
puntiforme q posta nel vuoto. Calcoliamo il gradiente del suo potenziale elettrico.
1
1 q
q
q
1 q r
r r
1
grad V0 grad
grad
.
2
4
r
4
r
4
r
r
4
r
r
0
0
0
0
Risulta dunque che grad V0 E 0 .
DEDUZIONE,
PRIMA EQUAZIONE DI MAXWELL E EQUAZIONI DI POISSON E LAPLACE.
La prima equazione di Maxwell si scrive
div E 0
0
D’altra parte la relazione tra potenziale elettrostatico e campo elettrostatico si scrive
E 0 grad V0
Sostituendo la seconda nella prima si ha
10
div grad V0
div grad V0
0
0
2V0 2V0 2V0
2
2
3
0
x
y
z
x, y , z
2V0 x, y , z
0
ottenendo così la così detta equazione di Poisson. Tale equazione si riduce alla così detta equazione
di Laplace in tutti quei punti dello spazio in cui non si abbia distribuzione di cariche (cioè fuori dai
conduttori).
DEFINIZIONE,
PROBLEMA DI DIRICHLET.
Il problema di Dirichlet si pone in questi termini: conosciamo il potenziale elettrostatico dei
conduttori e vogliamo calcolarlo nello spazio intorno ad essi utilizzando la equazione di Laplace.
Si tenga presente che se si ammette che il potenziale elettrostatico tende a zero come 1/r per r che
tende all’infinito, allora la soluzione del problema in questione esiste ed è unica (vedi il terzo
volume degli appunti personali di analisi matematica).
DEFINIZIONE,
PROBLEMA DI NEUMANN.
Il problema di Neumann si pone in questi termini: conosciamo la distribuzione delle cariche sulla
superficie dei conduttori e vogliamo il potenziale elettrostatico nello spazio intorno ad essi
utilizzando la equazione di Laplace.
V) IL DIPOLO ELETTRICO
DEFINIZIONE,
DIPOLO ELETTRICO. Definiamo tale una
coppia di cariche puntiformi di uguale valore
assoluto ma di segno opposto, che siano ad una
piccola distanza fra loro. Tipico esempio di
dipolo elettrico è la molecola dell’acqua.
DEFINIZIONE,
MOMENTO DEL DIPOLO. Dato un dipolo
elettrico definiamo suo momento il vettore
p avente modulo qδ, ove δ è la distanza fra le
cariche del dipolo, è avente verso che va dalla
carica negativa a quella positiva.
DEDUZIONE,
POTENZIALE DEL DIPOLO A GRANDE
DISTANZA DA ESSO. Le considerazioni che seguono sono valide nel caso in cui la dimensione
del dipolo sia trascurabile rispetto alla distanza del punto P da esso.
Il potenziale relativo ad un dipolo elettrico è dato da
11
1 q q
q r2 r1
4 0 r1 r2 4 0 r1 r2
q cos
1 pr cos
1 pz
2
3
4 0 r
4 0
4 0 r 3
r
V 0 P
In genere dunque il potenziale del dipolo si scrive
V 0 P
1
pz
4 0 r 3
DEDUZIONE,
POTENZIALE DEL DIPOLO IN FORMA ALTERNATIVA. Con immediate considerazioni
geometriche si vede che il potenziale del dipolo può scriversi anche
V 0 P
p r
4 0 r 3
1
DEDUZIONE,
POTENZIALE DEL DIPOLO IN FORMA ALTERNATIVA. Proviamo ora che il potenziale
del dipolo può scriversi come
V0 P
1
p grad
4 0
r
1
Si consideri infatti quanto segue.
1
r
1
x y z
grad 3 i 3 j 3 k
r
r
r
r
x2 y2 z2
1
pr cos
pz
1
p grad
3
3
r
r
r
Dunque
V0 P
1 pz
1
p grad
3
4 0
r 4 0 r
1
Questa formulazione del potenziale del dipolo verrà usata nello studio del campo elettrico nei
dielettrici.
DEDUZIONE,
CAMPO ELETTRICO DEL DIPOLO A GRANDE DISTANZA DA ESSO. Calcoliamo il
campo elettrico a partire dal potenziale.
12
E 0 P grad V0 P
1
4 0
p
z
3
4 0 x 2
2
2 2
x
y
z
grad
pz
x
2
y z
2
3
2 2
z
3
i y
x 2 y 2 z 2 2
z
3
j z
x 2 y 2 z 2 2
k
3
1
3 2
2
2
2 2
2
2 2
x y z z 2 x y z 2 z
p 3
2 xz
3
2 yz
i
j
k
5
5
2
2
2 3
4 0 2 2
2 2
2
2 2
2
2 2
x
y
z
x y z
x y z
p 3xz 3 yz r 3 3z 2 r
p
5 i 5 j
k
6
4 0 r
r
r
4 0
3xz 3 yz r 2 3z 2
5 i 5 j
r
r5
r
k
Dunque le componenti cartesiane del campo elettrico del dipolo sono
E 0 x P
p 3xz
4 0 r 5
p 3 yz
E 0 y P
4 0 r 5
p 3z 2 r 2
E 0 z P
4 0
r5
L’espressione vettoriale del campo elettrico del dipolo è invece
1 3 r p 1
E 0 P
r 3 p
4 0 r 5
r
DEDUZIONE,
COMPONENTI POLARI DEL CAMPO ELETTRICO DEL DIPOLO. La componente radiale
del campo elettrico del dipolo è data da
3xz x 3 yz y 3z 2 r 2 z
p 3x 2 z 3 y 2 z 3z 3 zr 2
5 5
6
r
r
r 4 0 r 6
r
r5
r
r6
r
pz
3x 2 3 y 2 3z 2 r 2 pz 6 3r 2 sin 2 3r 2 cos 2 r 2
6
4 0 r
4 0 r
r
p
E 0 r P E 0
r 4 0
pz
4 0 r
6
3r
2
r2
2 p cos
4 0
r3
1
La componente tangenziale è
E 0 P E 2 0 E 2 0 r
p sin
4 0 r 3
1
13
DEDUZIONE,
FORZA RISULTANTE AGENTE SU UN DIPOLO IMMERSO IN UN CAMPO
ELETTRICO ESTERNO. La carica negativa si trovi nel punto A. Quella positiva nel punto B.
L’energia potenziale che compete al bipolo in quanto immerso in un campo elettrico esterno si può
esprimere attraverso il valore del potenziale elettrico nel punto A. Infatti
V A
U qV0 A qV0 B qV0 A qV0 A 0
o
l
V A
q 0
qo
l
Abbiamo indicato l il versore del vettore AB ovvero di quello che chiamammo vettore . Adesso
trascuriamo l’infinitesiomo di ordine superiore rispetto e tiriamo in ballo il mcampo elettrico.
Abbiamo
U q
V0 A
q V0 A l E 0 A l q E 0 A p .
l
Ora passiamo al calcolo della forza risultante agente sul dipolo. Si ha
E 0 y A
E 0 x A
E 0 z A
i
F U E 0 x A p x E 0 y A p y E 0 z A p z p x
py
pz
x
x
x
E 0 y A
E 0 y A
E 0 x A
E 0 z A E 0 x A
E 0 z A
j p x
k
p x
py
pz
py
pz
y
y
y
z
z
z
Si osserva che la forza risultante è nulla nel caso di campo elettrico uniforme, che è probabilmente
quello a cui ci si può sempre rifare nel caso di molecole immerse in un campo elettrico. Senz’altro è
il caso delle molecole del dielettrico di un condensatore.
DEDUZIONE,
MOMENTO RISULTANTE AGENTE SU UN BIPOLO IMMERSO IN UN CAMPO
ELETTRICO ESTERNO. La carica negativa si trovi nel punto A. Quella positiva nel punto B. Il
momento risultante calcolato rispetto al punto B è dato da
B BA F A BA F A q E 0 A p E 0 A
Dunque il momento risultante rispetto al generico punto P si può scrivere ad esempio
P B F BP p E 0 A E 0 A p BP
Se il campo elettrico è uniforme la sollecitazione agente sul dipolo è una coppia di momento
p E 0
14
CAPITOLO II,
IL CAMPO ELETTROSTATICO IN PRESENZA DI
MATERIA
I) GENERALITA’
INTRODUZIONE. Nel precedente capitolo si è considerato il campo elettrico in assenza di corpi
materiali. Quando questi sono presenti essi interagiscono, per mezzo delle particelle cariche che li
costituiscono, con il campo elettrico.
In via qualitativa le cose avvengono in questo modo:
a)il campo elettrico altera la distribuzione delle cariche presenti nei corpi materiali,
b)queste creano a loro volta un campo elettrico che si sovrappone al campo originario e ne altera le
linee di forza.
In questo capitolo si forniscono gli strumenti per trattare questa complicata fenomenologia.
STRUTTURA DELLA MATERIA. Gli atomi che costituiscono un materiale sono neutri perché i
protoni del nucleo, positivi, bilanciano le cariche negative degli elettroni, che circondano il nucleo
stesso.
Le proprietà elettriche di un materiale dipendono dagli elettroni dello strato più esterno di ciascun
atomo che lo costituisce.
Se lo strato esterno è quasi completamente occupato, gli elettroni di tale strato sono fortemente
attratti dal nucleo e il materiale non ha la capacità di condurre corrente. In tale caso si parla di
materiali isolanti o dielettrici.
Se invece lo strato esterno è quasi completamente vuoto, allora si trova che gli elettroni che lo
occupano sono poco legati all’atomo, e qualunque campo elettrico, anche il più debole, è in grado di
spostarli all’interno del materiale. In tal caso si parla di materiali conduttori.
In un buon conduttore un elettrone per atomo è in grado di muoversi all’interno del conduttore
stesso. Per esempio nel rame il numero di elettroni liberi è di
8.4 10 28
e
m3
Si sottolinea che nei conduttori sono gli elettroni i soli portatori di carica. Le cariche positive degli
atomi restano invece immobili.
II) ELETTROSTATICA IN PRESENZA DI CONDUTTORI
OSSERVAZIONE SPERIMENTALE,
CONDUTTORE NEUTRO. Supponiamo di avere un conduttore neutro inserito in uno spazio
privo di campi elettrici esterni. Allora esistono solo i campi elettrici generati dai singoli elettroni
liberi che circolano per il conduttore e quelli generati dagli atomi immobili del reticolo. Si trova che
questi campi si anullano, istante per istante, in ogni punto dello spazio occupato dal conduttore (e
dello spazio esterno al conduttore stesso).
OSSERVAZIONE SPERIMENTALE,
CONDUTTORE NEUTRO IN UN CAMPO ELETTRICO. Supponiamo di avere un conduttore
neutro e di inserirlo in un campo elettrico esterno. Allora si verifica che alcune delle cariche libere
del conduttore vanno a costituire uno strato di pochi angstrom, sulla superficie del conduttore
15
stesso. Il campo elettrico generato da questa distribuzione di cariche è sempre tale da bilanciare il
campo elettrico iniziale, nello spazio occupato dal conduttore.
DEDUZIONE,
CONDUTTORE CARICO. Supponiamo ora di mettere, in qualche modo, degli elettroni in un
conduttore altrimenti neutro. Atteso l’equilibrio, cioè l’assenza di un moto macroscopico di cariche,
allora il campo elettrico all’interno del conduttore deve essere nullo. Se così non fosse si avrebbe
infatti ancora moto macroscopico di cariche.
Se il campo elettrico dentro al conduttore è nullo ne segue, per la legge di Gauss, che l’interno del
conduttore è nuovamente neutro. Ma allora dove sono finiti gli elettroni aggiunti al conduttore?
Per esclusione si deve concludere che essi sono tutti sulla superficie del conduttore 2. Qui tali
elettroni costituiscono una distribuzione tale da costituire un campo elettrico il cui valore è ovunque
nullo all’interno del conduttore.
DEDUZIONE,
IL CONDUTTORE E’ EQUIPOTENZIALE. Poiché il campo elettrostatico è nullo nello spazio
occupato da un conduttore, ne segue che la sua primitiva, il potenziale elettrostatico, è costante in
tale spazio.
DEDUZIONE,
ORTOGONALITA’ DEL CAMPO ELETTROSTATICO ALLA SUPERFICIE. Se lo spazio
occupato da un conduttore è equipotenziale, in particolare la sua superficie è una superficie
equipotenziale. Ricordando che il gradiente di una funzione è ortogonale, punto per punto, ad una
superficie equipotenziale di tale funzione, concludiamo che il campo elettrico, in quanto opposto
del gradiente del potenziale elttrico, è ortogonale punto per punto alla superficie del conduttore.
DEDUZIONE,
TEOREMA DI COULOMB. Vogliamo calcolare il campo elettrico in un punto infinitamente
prossimo alla superficie di un conduttore. Prendiamo allora un
punto P sulla superficie del conduttore. Sia dS un intorno di P.
Costruiamo poi la superficie cilindrica indicata in figura. Se le
dimensioni di tale superficie tendono a zero possiamo scrivere
che
cilindro E E 0 dS
cilindro
E 0 dS
mantello
In base poi alla legge di Gauss tale flusso vale
E 0 P dS
dS
0
E 0 P
base
dS
0
E 0 dS E 0 P dS
E 0 dS
base
e dunque si ha
0
2
Sperimentalmente si constata che le cariche in esubero si ditribuiscono su uno strato di pochi angstrom ai limiti
del conduttore.
16
III) ELETTROSTATICA IN PRESENZA DI DIELETTRICI
OSSERVAZIONE SPERIMENTALE,
STRUTTURA DEI DIELETTRICI. Esistono dielettrici che hanno molecole dotate di momento
di dipolo permanente, tipo NaCl, dette molecole polari, e dielettrici le cui molecole non hanno
momento di dipolo proprio, dette molecole non polari. Su queste ultime è il campo esterno che
induce un momento di dipolo per deformazione.
L’azione di orientamento dei dipoli (o naturalmente presenti nel materiale, o indotti dal campo
esterno) prende il nome di polarizzazione. La polarizzazione può determinare in dielettrici
inizialmente neutri sia una densità di carica superficiale p che una densità di carica volumica p .
Per i dipoli dei dielettrici usiamo la stessa simbologia introdotta nel caso del dipolo astratto già
studiato. Diciamo cioè che essi hanno momento di dipolo p con p q il cui modulo, la cui
direzione ed il cui verso dipende dal campo elettrico esterno.
DEFINIZIONE,
VETTORE INTENSITA’ DI POLARIZZAZIONE. Definisco vettore intensità di polarizzazione
di un dielettrico il vettore
P
N p
V
dove N è il numero di particelle nel volume V e
p è il valore medio del momento di dipolo
delle particelle del dielettrico all’interno di tale volume.
Il volume V deve essere sufficentemente piccolo da fornire per P valori che variano con
continuità e abbastanza grande da consentire una media affidabile3 per p .
OSSERVAZIONE SPERIMENTALE,
DIELETTRICI ISOTROPI. Nel caso in cui il dielettrico sia isotropo si riscontra che P è
proporzionale al campo elettrico esterno (quello che produce la polarizzazione). In questo caso si
dice che il dielettrico ha un comportamento lineare.
DEFINIZIONE,
SUSCETTIVITA’ DIELETTRICA. Nel caso di dielettrico isotropo si pone
P 0 E
La costante prende il nome di suscettività dielettrica del mezzo. Essa è una grandezza
adimensionata ed è positiva, per ogni dielettrico lineare. Il fatto che sia positiva è dovuto al fatto
V 1m 3 10 18 m 3 è certamente abbastanza piccolo da poter essere confuso con
12
un punto, pur contenendo un numero abbastanza alto di atomi (per esempio 10 atomi di idrogeno) da poter
3
Per esempio un volume
fare una media.
17
che i dipoli molecolari si allineano al campo elettrico e dunque P è parallelo ad E . Questo vuole
dire, tra l’altro, che nei dielettrici il campo elettrico esterno tende ad essere smorzato.
IV) DENSITA’ DI CARICA INDOTTA DALLA
POLARIZZAZIONE DEL DIELETTRICO
DEDUZIONE,
POTENZIALE ELETTROSTATICO CREATO
DA UN DIELETTRICO. Consideriamo un
dielettrico di volume V. Un suo volume dV si può
considerare un dipolo di momento N p P dV .
Il potenziale elettrostatico in P determinato da un
volumetto dV risulta dato da
1
N p grad
4 0
r
1
1
P dV grad
4 0
r
dV0 P
1
nel sistema di riferimento indicato in figura.
Se però rototrasliamo il sistema di riferimento in modo che la sua origine vada a coincidere con il
punto P e se con r indichiamo il vettore che va da P al centro del dipolo, l’espressione del
potenziale perde il segno meno4 e si ha
dV0 P
1
P grad dV
40
r
1
Allora il potenziale in P, generato dai dipoli di tutto il volume V di dielettrico, risulta dato da
V 0 P
1
P
grad
dV
4 0 V
r
1
Ricordando ora che F grad g div g F gdiv F si scrive
V 0 P
1
1 1
div
P
div
P
dV
4 0 V r r
4 0
1
1
1
div P dV div PdV
r
r
V
V
In base poi al teorema della divergenza si può concludere
1 r , prima del cambio di sistema di riferimento, ha lo stesso valore su superficie sferiche
di centro O, e punta verso il centro. Il vettore gradiente di 1 r dopo il cambio di sistema di riferimento ha le
4
Il vettore gradiente di
stesse caratteristiche solo che punta il punto P. In pratica dunque i due gradienti hanno stesso valore, stessa
direzione, ma verso opposto.
18
V0 P
1
1
P n dV
4 0 V r
4 0
1
1
div
P
V r dV
DEDUZIONE,
DENSITA’ DI CARICA DI POLARIZZAZIONE. Ora si osserva una cosa curiosa, e cioè che se
considerassimo il dielettrico come una distribuzione continua di cariche con densità di carica
volumica pol e densità di carica superficiale pol allora, rispetto ad un sistema di riferimento con
origine in P il potenziale elettrostatico si scriverebbe
V 0 P
1
4 0
V
pol
r
dV
1
4 0
V
pol
r
dV
Confrontando con l’espressione ottenuta per il potenziale elettrostatico prodotto dal dielettrico si
osserva che in esso si riscontra una densità di carica superficiale ed una densità di carica volumica
di polarizzazione date rispettivamente da
pol P n
pol div P
V) IL CAMPO ELETTRICO IN PRESENZA DI DIELETTRICI
DEDUZIONE,
PRIMA EQUAZIONE DI MAXWELL IN PRESENZA DI DIELETTRICI. La prima
equazione di Maxwell all’interno di un dielettrico diviene
lib pol lib div P
div E
0
0
che possiamo anche scrivere
P
div E
0
lib
0
OSSERVAZIONE,
SECONDA EQUAZIONE DI MAXWELL IN PRESENZA DI DIELETTRICI. La seconda
equazione di Maxwell resta inalterata anche in presenza di dielettrici poiché la natura delle cariche
che originano il campo elettrico non influisce sulle caratteristiche dello stesso. Resta ancora valida
dunque la relazione
rot E 0
19
DEFINIZIONE,
IL VETTORE SPOSTAMENTO ELETTRICO. In genere si usa ragionare, anziché con il
vettore P , con un altro vettore, detto spostamento elettrico, definito dalla relazione seguente
D 0 E P
Si osserva che questo vettore risulta determinato dalle cariche libere, cioè da quelle cariche
direttamente misurabili, infatti si ha evidentemente
div D lib
DEFINIZIONE,
COSTANTE DIELETTRICA RELATIVA E ASSOLUTA. Nel caso di comportamento lineare
del dielettrico si ha
P 0 E D 0 E P
D 1 0 E
La costante 1 prende il nome di costante dielettrica relativa del mezzo e si pone
r 1
Dunque la relazione fra spostamento elettrico e campo elettrico in mezzi isotropi diviene
D r 0 E
Se definiamo poi la costante dielettrica assoluta come
r 0
tale relazione si scrive
D E
OSSERVAZIONE SPERIMENTALE,
VALORI DELLA COSTANTE DIELETTRICA RELATIVA. La costante dielettrica relativa
assume valori compresi da 1 a 10. Per l’acqua ad esempio essa vale 8 (a pressione e temperatura
ordinarie), mentre per l’aria vale 1,00057. Questo fa dell’aria una buona approssimazione, dal punto
di vista del campo elettrostatico, del vuoto assoluto.
20
TABELLA,
PRIMA E SECONDA EQUAZIONE DI MAXWELL NEI DIELETTRICI.
PRIMA EQUAZIONE DI MAXWELL
SECONDA
EQUAZIONE DI
MAXWELL
CASO GENERALE
div 0 E P lib div D lib
rot E 0
ISOTROPIA
div r 0 E lib div E lib div D lib
rot E 0
ISOTROPIA E
OMOGENEITA’
div E
lib
div E lib div D lib
0 r
rot E 0
DEDUZIONE,
CAMPO ELETTRICO DI UNA CARICA PUNTIFORME IN UN DIELETTRICO.
Supponiamo di avere una carica q immersa in un dielettrico omogeneo e isotropo di costante
dielettrica relativa r . Allora il campo elettrico da essa generato si scrive
1 q r
1
q r
E r
2
4 r r 4 0 r r 2 r
DIMOSTRAZIONE. Poiché la legge di Gauss si scrive in queste ipotesi
div E
0 r
dove è la densità della carica considerata, si può ammettere che l’espressione del campo elettrico
sia proprio quella indicata.
DEDUZIONE,
LA LEGGE DI COULOMB NEI MEZZI DIELETTRICI. In un mezzo dielettrico isotropo la
legge di coulomb si scrive
q
F0 r
4 r 0
n
i 1
r ri
r ri
qi
2
r ri
DIMOSTRAZIONE. La dimostrazione è immediata
conseguenza della precedente deduzione.
DEDUZIONE,
SUPERFICIE DI SEPARAZIONE E CAMPO
ELETTRICO. Consideriamo la superficie di separazione fra due dielettrici accostati. Nel
passaggio dall’uno all’altro il campo elettrico conserva la sua componente tangente alla superficie.
Dunque
21
E t1 E t 2
DIMOSTRAZIONE. Nella illustrazione è rappresentata in verde una superficie di separazione fra
due dielettrici diversi. Il rettangolo ABCD sia tale da avere i lati AD e BC paralleli alla superficie
stessa
e gli altri due ortogonali ad essa ed intersecanti la stessa. Si fa presente che ci si considera
nell’intorno di un punto della superficie.
Se calcoliamo la circuitazione del campo elettrico lungo tale rettangolo, in base alla seconda
equazione di Maxwell (conservatività del campo elettrico), si ha
||
||
||
||
||
||
E d l E 1 BC E 1 DA 0 E 1 BC E 2 DA E 1 E 2
dove si è trascurato il contributo della integrazione sui lati AB e CD i quali si possono assumere
molto piccoli rispetto gli altri due.
La tesi è dunque verificata.
DEDUZIONE,
SUPERFICIE DI SEPARAZIONE E SPOSTAMENTO
ELETTRICO. Consideriamo la superficie di separazione fra
due dielettrici accostati. Nel passaggio dall’uno all’altro lo
spostamento elettrico conserva la sua componente normale alla
superficie. Dunque
Dn1 Dn 2
DIMOSTRAZIONE. Nella illustrazione è rappresentata in
verde una superficie di separazione fra due dielettrici diversi.
Consideriamo nell’intorno di un punto di tale superficie la superficie ‘a barattolo’ indicata in figura.
Il flusso del vettore spostamento attraverso tale superficie è dato da
D D1 n S D2 n S D 1 S D 2 S
Ma la prima equazione di Maxwell o, se si vuole, la legge di Gauss, ci dicono anche che D 0 .
Confrontando le due relazioni ottenute otteniamo la tesi.
DEDUZIONE,
SUPERFICIE DI SEPARAZIONE E CAMPO ELETTRICO. Attraverso la superficie di
separazione fra due dielettrici la componente normale del campo elettrico cambia secondo la
seguente legge
1r E 1 2 r E 2
DIMOSTRAZIONE. In base al precedente teorema si ha
D 1 D 2 1 E 1 2 E 2 1r E 1 2 r E 2
DEDUZIONE,
22
RIFRAZIONE DELLE LINEE DI FORZA. Ricaviamo ora un legame fra l’angolo che il campo
elettrico forma con la normale alla superficie di separazione e le costanti dielettriche relative dei
mezzi.
In base a considerazione geometriche (vedi figura) abbiamo
E ||1
tan
1
tan 1 E 2 1r
E 1
||
tan 2 E 1 2 r
tan E 2
2
E 2
VI) CAPACITA’ E CONDENSATORI
DEDUZIONE,
CARICA ELETTRICA E POTENZIALE ELETTROSTATICO.
Si consideri un conduttore di forma qualsiasi isolato nello spazio. Se a questo conduttore viene
fornita una carica Q, la sua superficie si porta ad un potenziale V rispetto ad esempio all’infinito,
dove si può assumere lo zero del potenziale stesso. Si vuole dimostrare che il potenziale assunto dal
conduttore è direttamente proporzionale alla carica ad esso fornita secondo un coefficiente legato
solo alla geometria del conduttore stesso.
DIMOSTRAZIONE. Consideriamo il caso particolare di un conduttore avente la forma di una
sfera piena. Ricaviamo l’espressione del potenziale di tale conduttore quando gli sia attribuita una
carica Q.
Intanto sappiamo che la carica si andrà a distribuire sulla superficie della sfera. Inoltre sappiamo
che, per via della simmetria del conduttore, tale distribuzione sarà uniforme. Chiamiamo σ la
distribuzione uniforme di carica sulla sfera.
L’equazione parametrica della superficie sferica è
x R sin cos
y R sin sin
z R cos
0,
0,2
Il potenziale del conduttore è il valore del potenziale elettrostatico sulla sua superficie, ovvero in
corrispondenza di un pinto qualunque della sua superficie, per esempio il punto P 0,0, R . Si ha
V0 V0 P
1
4 0
PQdS
ove il punto Q è il punto che scorre sulla superficie della sfera. Si ha
23
P 0,0, R
PQ 2 R 1 cos
Q R sin cos , R sin sin , R cos
V0
1
4 0 2 R 1 cos
4 0
2
R 2 sin
2R
1 cos
0 0
dS
2
4 0 2 R
dd
2R 2
4 0
A2 B 2 C 2
1 cos
0 0
2R
0
sin
1 cos
dd
d
1
4R
Q
4 R
4 R
1
2
0
0
Si vede dunque come il potenziale della sfera sia direttamente proporzionale alla carica attraverso
un coefficiente che dipende dal raggio della sfera.
DEFINIZIONE,
CAPACITA’ DEL CONDUTTORE ISOLATO. Si consideri il conduttore isolato di cui nel
teorema precedente. Il coefficiente di proporzionalità fra la carica che esso possiede ed il suo
potenziale viene chiamato capacità ed indicato col simbolo C. Si pone cioè
C
Q
V
La capacità si misura in Farad (simbolo F) e risulta
Farad
Coulomb
.
Volt
DEFINIZIONE,
CONDENSATORE. Consideriamo due conduttori nel vuoto che siano stati caricati con cariche
uguali in modulo, ma di segno opposto. Se la geometria dei due conduttori è tale che tutte le linee di
forza del campo elettrico (generato dalle due distribuzioni di cariche) hanno origine in un
conduttore e termine nell’altro, allora il sitema prende il nome di condensatore.
I due conduttori vengono detti armature del condensatore.
OSSERVAZIONE,
REALIZZAZIONE DEL CONDENSATORE. In
pratica si può realizzare un condensatore procedendo
come segue. Si prende un conduttore e gli si attribuisce
una carica Q. Gli si costruisce attorno un involucro
conduttore. Si collega la superficie esterna
dell’involucro
conduttore
ad
un
conduttore
infinitamente più grande (a terra, come si dice). In
questo modo si realizza la situazione in figura.
Si osserva che al secondo conduttore, quello esterno,
non è stata aggiunta nessuna carica. Esso presenterà alla fine carica –Q poiché, al momento del
collegamento a terra della sua faccia esterna, perde la carica Q indotta su tale faccia dal conduttore
interno.
24
DEDUZIONE,
DIFFERENZA DI POTENZIALE FRA LE ARMATURE DI UN CONDENSATORE. La
differenza di potenziale fra le armature di un condensatore, in valore assoluto, è direttamente
proporzionale al valore assoluto della carica presente su ciascuna delle due armature.
DIMOSTRAZIONE. Consideriamo il caso del dispositivo rappresentato in figura. Abbiamo una
palla conduttrice, di raggio r1 , caricata con una carica complessiva Q; c’è poi un guscio conduttore,
ad essa concentrico, di raggio r2 r1 , la cui superficie esterna sia collegata a terra.
Il campo elettrico compreso fra le due armature, in base alla legge di Gauss e a considerazioni sulla
simmetria del sistema, è dato da
E0
Q
4 0 r 2
dove è il versore radiale di un sistema di riferimento polare
avente centro nel centro del sistema. Ne segue che il potenziale
in tale spazio è
V0 r
Q
4 0 r
2
dr
Q
1
4 0
r
2
dr
Q
4 0
r 1 c
Allora la differenza di potenziale, in modulo, fra le due armature risulta
V0 r1 V0 r2
Q
4 0
1
r1
Q
4 0
r2
1
1 1
Q r2 r1
Q
4 0 r1 r2 4 0 r1 r2
4 0
Q
r2 r1
r
r
12
E la tesi risulta evidentemente dimostrata.
DEFINIZIONE,
CAPACITA’ DEL CONDENSATORE. Definiamo capacità del condensatore il rapporto fra il
modulo delle caricha presente su ciascuna delle due armature, e la differenza, in valore assoluto, fra
i potenziali delle due armature stesse.
La definizione è ben posta in virtù della precedente deduzione.
DEDUZIONE,
CAPACITA’ DEL CONDENSATORE SFERICO. In base alla definizione di capacità del
condensatore, per il condensatore sferico si ha
0 S1 S 2
4 0 r1 r2 0 4r1 4r2
Q
C
r2 r1
r2 r1
d
Q r2 r1
4 0 r1 r2
2
2
DEDUZIONE,
CAPACITA’ DEL CONDENSATORE PIANO. Intanto si parla di condensatore piano quando le
due armature sono due lastre piane che si affacciano una sull’altra. In questo caso il campo elettrico
fra le due armature è quello del doppio strato piano, per cui si ha
25
V0 x dx x c V0 0 V0 d
0
0
0
S
Qd
d
d
0
0S
0S
E0
Allora la capacità di questo genere di condensatore è
C
Q
Qd
0S
0S
d
DEDUZIONE,
CONDENSATORE CON DIELETTRICO. L’inserimento fra le due armature di un condensatore
di un dielettrico ha l’effetto di aumentare la sua capacità di un fattore pari alla costante dielettrica
relativa del materiale.
DIMOSTRAZIONE. Sappiamo che, in caso di mezzo isotropo e omogeneo di costante dielettrica
relativa r la legge di Gauss siscrive
D dS qtot 0 r E dS qtot E dS
qtot
0 r
Se dunque si considera una superficie a forma di parallelepipedo che racchiuda una delle due
armature del condensatore e si calcola il flusso del campo elettrico attraverso di essa si ha
E
dS
E
S
q
S
ES tot ES
E
0 r
0 r
0 r
E dS S
0 r
Procedendo adesso al calcolo della capacità come si è fatto nel caso del condensatore senza
dielettrico si ha
C
Q
Qd
0S
r
0S
d
Ciò che dimostra la tesi.
VII) ENERGIA POTENZIALE E FORZE ELETTROSTATICHE
DEFINIZIONE,
ENERGIA POTENZIALE DI UNA DISTRIBUZIONE DI CARICHE. In ogni distribuzione di
cariche è immagazzinata una energia che corrisponde al lavoro che è stato necessario fare per
costruire il sistema.
26
Questa energia viene restituita dal sistema quando si lasciano libere di muoversi le cariche che lo
compongono. L’energia che viene messa a disposizione quando il sistema si disgrega si chiama
energia potenziale, o energia libera, e si indica con il simbolo U.
DEDUZIONE,
ENERGIA POTENZIALE DI UNA DISTRIBUZIONE DISCRETA DI CARICHE. L’energia
potenziale di una distribuzione discreta di n cariche è data da
U0
1 n
2 i j
qi q j
4 0 r i r
1 n
qi
2 i 1 i j
j
qj
4 0 r i r
j
1 n
r
q
V
i 0i i
2 i 1
dove con V0i indichiamo il potenziale elettrostatico determinato da tutte le cariche della
distribuzione, ad eccezione della carica i-ma.
DIMOSTRAZIONE. Supponiamo di avere le quattro cariche q1 , q2 , q3 , q4 ad una distanza infinita
fra loro, tale che esse non risentano le une del campo elettrico delle altre.
Portiamo ora la carica q1 nella posizione r 1 . Per fare questo trasferimento non facciamo alcun
lavoro perché spostiamo la carica in assenza di un campo elettrico esterno.
Ora portiamo la carica q2 nella posizione r 2 . Questa volta stiamo spostando una carica, la q2 ,
all’interno del campo elettrico di una seconda carica, la q1 . Questo richiede un lavoro. Ma quanto
vale questo lavoro? La forza applicata sulla carica q2 , in base alla legge di Coulomb, è
1
F 0 12 r 2
40
r 2 r1
r 2 r1
q1q2
2
r 2 r1
la quale è una forza conservativa di potenziale
1
q1q2
f 1 2 r 2
40
r 2 r1
Per vedere questo fatto si puo considerare la carica q1 nel centro del sistema di riferimento. In tal
caso si ha
F 012 x, y, z
q1q2
1
40
x
y 2 z 2 2
3
2
x
q1q2
1
f 12 x, y, z
y
1
4
0
z
x 2 y 2 z 2 2
Allora il lavoro che un ente esterno fa per portare q2 nella posizione r 2 , ammesso che questo
spostamento avvenga in modo infinitamente lento, deve essere l’opposto del lavoro delle forze del
campo. Cioè si ha
27
L2 f 12 r 2 f 12 f 12 r 2 f 12
q1q2
1
f 12 r 2 0 f 12 r 2
40 r r
2
1
Per portare ora la carica q3 nella posizione r 3 dobbiamo procedere come sopra, con la differenza
però che ora ci muoviamo nel campo elettrico generato da due cariche, non più da una sola.
Avvalendoci del principio di sovrapposizione degli effetti, per analogia a quanto visto sopra, si ha
che il lavoro che un ente esterno deve fare per portare ora la carica q3 nella posizione r 3 è dato da
L3
1
40
q1q3
r 3 r1
1
40
q2 q3
r 3 r 2
Per portare infine la carica q4 nella posizione r 4 si deve compiere il lavoro
L4
1
40
q1q4
r 4 r1
1
40
q2 q4
r4 r2
1
40
q3 q4
r4 r3
Si conclude che il lavoro che si deve fare per ‘costruire’ la distribuzione discreta di cariche
rappresentata in figura è pari a
1
q1q3
q2 q3
1
L L2 L3 L4
40
40
40
r 2 r1
r 3 r1
r 3 r 2
1
qi q j
q3 q4 1
q1q4
q2 q4
1
1
1
40 2 i j 40
40 r 4 r 1 40 r 4 r 2
r4 r3
r j ri
1
q1q2
Si osservi che il fattore moltiplicativo 1
2
è necessario perché altrimenti ciascun addendo sarebbe
sommato due volte.
Questo lavoro rappresenta ciò che abbiamo definito energia potenziale della distribuzione di carche.
DEDUZIONE,
ENERGIA POTENZIALE DI UNA DISTRIBUZIONE CONTINUA DI CARICHE. Ora la
distribuzione di cariche da ‘costruire’ sia continua. Riferendoci alla espressione seguente dellla
energia potenziale di una distribuzione continua di cariche
U0
1 n
qiV0i r i
2 i 1
28
se sostituiamo a qi l’espressione r d , dove si introduce la densità volumica di carica e
l’elemento di volume, allora abbiamo
U0
1
V
r
0 r d
2
che è appunto l’espressione della energia potenziale di una distribuzione continua di cariche su un
volume Ω. Si intende che V 0 r è il potenziale elettrostatico, in r , di tutta la distribuzione di
carica (meno l’elemento di carica r d , si dovrebbe dire; ma tale specificazione è superflua,
essendo tale elemento infinitesimo).
DEDUZIONE,
ENERGIA POTENZIALE DI UN CONDUTTORE. Nel caso di un conduttore la carica è
distribuita con continuità solo sulla superficie del conduttore stesso. Dunque l’energia potenziale di
un conduttore occupante un dominio Ω è data da
U0
1
V
r
0 r dS
2
in cui si intende che r sia la densità di carica superficiale del conduttore stesso. Poiché il
potenziale elettrostatico di un conduttore è il medesimo in ciascun punto della sua superficie, allora
V0 r rappresenta il potenziale sulla superficie del conduttore stesso ed è una costante che può
essere tirata fuori dal segno di integrale. Si ha allora
1
1
U 0 V0 r dS V0Q
2
2
dove
1) V0 è il potenziale della superficie del conduttore;
2) Q è la carica complessivamente presente sulla superficie del conduttore.
DEDUZIONE,
ENERGIA POTENZIALE DI PIU’ CONDUTTORI. Se i conduttori sono più di uno l’energia
potenziale del loro insieme è data da
U0
1 n
V0iQi
2 i 1
dove
1) V0i è il potenziale della superficie del conduttore i-mo;
29
2) Qi è la carica complessivamente presente sulla superficie del conduttore i-mo.
DEDUZIONE,
ENERGIA POTENZIALE DI UN CONDENSATORE. L’energia potenziale di un condensatore
di carica Q e differenza di potenziale V0 è data da
1
1 Q2
2
U 0 C V0
2
2 C
DIMOSTRAZIONE. L’energia potenziale di un condensatore è l’energia potenziale di due
conduttori aventi carica uguale ma di segno opposto. Dunque essa è data da
U0
1
V01Q1 V02Q2 1 V01Q V02Q 1 Q V01 V02 1 QV0
2
2
2
2
Tenendo poi presente che la capacità del condensatore vale
C
Q
V0
si conclude che
1
1 Q2
2
U 0 C V0
2
2 C2
cioè la tesi.
DEFINIZIONE,
DENSITA’ DI ENERGIA POTENZIALE. Si definisce densità di energia potenziale di una
distribuzione di cariche una funzione di punto u uP tale che risulti
U
1
u P dV
2
dove U è l’energia potenziale della distribuzione di cariche e l’integrale si intende esteso a tutto lo
spazio in cui è non nullo il campo elettrico determinato dalla distribuzione di cariche stessa.
DEDUZIONE,
DENSITA’ DI ENERGIA POTENZIALE. La densità di energia potenziale di una distribuzione
di cariche risulta essere la funzione
1
u P E 2 P
2
dove ε è la costante dielettrica assoluta del mezzo in cui è inserita la distribuzione di cariche.
DIMOSTRAZIONE. Dimostriamo la tesi nel caso di un condensatore piano. Si tenga presente
però che essa è dimostrabile anche nel caso generale.
30
L’energia potenziale di un condensatore nel vuoto è
1
1 Q2
2
U 0 C V0
2
2 C
Il condensatore piano nel vuoto è caratterizzato dalla capacità
C
0S
d
Dunque l’energia potenziale che compete alla distribuzione di carica che si ha nel caso di un
condensatore piano nel vuoto è
U0
1 Q 2 1 dQ 2
2 C 2 0S
Scrivendo ora la carica in funzione della densità superficiale di carica si ha
U0
1 dS 2 2 1 dS 2
2 0S
2 0
Tenendo presente ora che il campo elettrico prodotto da questa distribuzione di carica è quello del
doppio strato piano, cioè ovunque nullo, tranne che fra le due armature, dove è costante e vale
, allora si ha
0
1 dS 2 1 dS 0 2 1
2
U0
dS 0 E 0
2
2 0
2 0
2
Dividendo per il volume racchiuso dal condensatore, per lo spazio cioè in cui il campo elettrico è
non nullo, si ha
U0 1
2
0 E0
Sd 2
espressione che, nel caso di presenza di dielettrico si scrive 1 E 2 . E’ evidente che questa quantità
2
rappresenta la densità di energia potenziale per la distribuzione di carica rappresentata da un
condensatore piano. Essa però fornisce in realtà la densità di energia potenziale per qualunque
distribuzione di carica.
VERIFICA. Per dare una parziale verifica della
generalità della formula della densità di energia
potenziale, trovata in un caso particolare, proviamone
la validità nel caso di una distribuzione sferica di
carica, nel caso cioè di un conduttore sferico a cui sia
assegnata una carica.
Secondo quanto detto in precedenza la densità di
energia potenziale di questa distribuzione sarebbe data
31
da
2
1
1 1 q
1 1 q2
2
u r E r
2
2 4 r 2
2 16 2 r 4
dove si è considerata la presenza, intorno alla sfera, di un dielettrico. E dove si è introdotto un
sistema di riferimento polare con origine nel centro della sfera.
Per verificare tale formula dobbiamo allora provare che integrandola nello spazio in cui è non nullo
il campo elettrico prodotto dalla sfera (cioè intorno alla sfera stessa) si abbia l’energia potenziale
della sfera. Procediamo.
2
2
R 0 0
R 0
2
ur r sin dddr
1 1 q2 2
1 q2
r
sin
d
d
dr
0 2 16 2 r 4
2 16 2
2
sin
d ddr
2
0 r
R 0
1 q2
sin
1 q2
1
1 q2 1
1 q2 1
0
2
d
dr
dr
sin
d
cos
R 0 r 2
2 16 2
2 8 R r 2 0
2 8 r R
2 4 R
Otteniamo allora una espressione identica a quella che avremmo ottenuto partendo dalla formula
trovata per l’energia potenziale di un conduttore (vedi sopra). Quindi la verifica è positiva.
DEDUZIONE,
FORZA FRA LE ARMATURE DI UN CONDENSATORE PIANO. La forza con cui le due
armature di un condensatore piano si attraggono ha modulo
F
1 Q2
2 0S
DIMOSTRAZIONE. Questa dimostrazione è un modo per mostrare come si possa risalire alle
forze esercitantesi fra varie componenti di una distribuzione di carica a partire dalla energia
potenziale della distribuzione stessa.
Sappiamo che l’energia potenziale di un condensatore piano nel vuoto è
1 Q2x
U0
2 0S
dove x è la distanda fra le due armature. Questa emergia, lo si ricorda, rappresenta il lavoro che è
stato fatto per mettere assieme le cariche presenti sulle due armature, per metterle nella geometri
che occupano ora.
Se adesso lasciassimo che le due lastre, che si attraggono, si avvicinassero di una quantità dx,
l’energia potenziale del sistema diminuirebbe e diventerebbe
1 Q 2 x dx 1 Q 2 x 1 Q 2 dx
1 Q 2 dx
U0
U0
2
0S
2 0S 2 0S
2 0S
|
La quntità di energia che il sistema perde viene da esso rilasciata sottoforma di lavoro meccanico, il
lavoro che si esplica quando le due armature si avvicinano. Tale lavoro è il prodotto della forza
attrattiva fra le due armature per lo spostamento delle stesse. Si ha cioè
32
1 Q 2 dx
1 Q2
L Fdx F
2 0S
2 0S
Il che dimostra la tesi.
33
CAPITOLO III,
CORRENTE ELETTRICA E SORGENTI DI FORZA
ELETTROMOTRICE
I)INTENSITA’ DI CORRENTE E DENSITA’ DI CORRENTE
INTRODUZIONE. Cariche elettriche in moto danno luogo a correnti elettriche. Si distinguono
due tipi fondamentali di correnti elettriche: quelle di conduzione e quelle di convezione.
1)CORRENTI DI CONDUZIONE. Le correnti elettriche di maggior interesse sono le correnti di
conduzione. Esse si manifestano nei mezzi per la presenza di cariche libere che, non essendo
vincolate al reticolo cristallino, possono muoversi al suo interno.
2)CORRENTI DI CONVEZIONE. Le correnti di convezione sono dovute a portatori di carica
(corpi o particelle elettricamente cariche) che si muovono trascinando con sé anche le cariche
elettriche su essi depositate. Queste possono essere sia libere che vincolate. Correnti di convezione
possono prodursi in particolare nelle soluzioni elettrolitiche per il moto di ioni.
Nei gas possono essre presenti elettroni in moto che danno luogo a correnti di conduzione; in
opportune condizioni di pressione essi possono urtare le molecole del gas, ionizzandole, cioè
scindendole in ioni positivi e negativi; questi nuovi portatori di carica a loro volta si mettono in
moto producendo una corrente di convezione e ulteriori ionizzazioni.
OSSERVAZIONE SPERIMENTALE,
VELOCITA’ DI SCORRIMENTO. Nei conduttori i portatori di carica possiedono una velocità di
agitazione termica a cui corrisponde uno spostamento medio nullo (nei metalli la velocità di
agitazione termica degli elettroni si aggira sui 10^5 m/s).
Nel caso in cui il conduttore sia inserito in un campo elettrico, allora lo spostamento medio dei
portatori di carica risulta diverso da zero. Ad esso corrisponde una velocità v detta velocità di
scorrimento o velocità di deriva (nei metalli la velocità di scorrimento degli elettroni non supera
mai il metro al secondo).
La velocità di scorrimento ha la direzione del campo elettrico ed il verso concorde ad esso se le
cariche in moto sono positive, verso opposto in caso contrario.
DEFINIZIONE,
INTENSITA’ DI CORRENTE ELETTRICA. Consideriamo una superficie S orientata dal
versore normale n . Definiamo intensità di corrente il limite
i t lim
t 0
q dq
t dt
dove vale il seguente significato dei simboli:
1) q è la carica netta che attraversa la superficie nel verso di n nell’intervallo di tempo t : la
carica positiva q va sommata se se il suo moto è concorde a n , va sottratta altrimenti; la carica
negativa q va sottratta se il suo moto è concorde a n , va sommata altrimenti;
34
2) t è l’intervallo di tempo nel quale si considera il transito delle cariche.
La corrente elettrica è una grandezza scalare, in generale variabile nel tempo. Essa dipende dalla
superficie S scelta e, a parità di superficie, dall’orientazione ad essa assegnata; in particolare
invertendo l’orientazione (cambiando verso ad n ) il numero reale che la esprime inverte il prprio
segno.
La corrente elettrica ha dimensione fisica di ampere (A).
DEFINIZIONE,
DENSITA’ DI CORRENTE ELETTRICA. La descrizione locale (in ogni punto P ed in ogni
istante t) del moto delle cariche è fornita dal vettore densità di corrente elettrica J P, t .
Definiamo densità di corrente elettrica la somma vettoriale
J P , t P , t v P , t P , t v P , t
dove vale il seguente significato dei simboli:
1) P, t è la densità di carica positiva;
2) v P, t è il campo di velocità associato alla densità di carica positiva;
3) P, t è la densità di carica negativa;
4) v P, t è il campo di velocità associato alla densità di carica negativa.
Il vettore J P, t definisce nello spazio un campo vettoriale definito campo di corrente. Il suo
modulo ha dimensione fisica di coulomb su secondo su metro quadro, vale a dire di ampere su
metro quadro (A/m^2).
Dato che le cariche dei due segni hanno, in generale, velocità diversa, la densità di corrente può
essere non nulla anche nei punti in cui è nulla la densità di carica. Ad esempio nei metalli, anche se
elettricamente neutri, si manifesta corrente elettrica quando in essi migrano gli elettroni mentre
restano fermi i nuclei, dotati di carica positiva e legati al reticolo cristallino. Nelle soluzioni
elettrolitiche invece, pur elettricamente neutre, la corrente elettrica è dovuta agli ioni positivi ed agli
ioni negativi che si muovono con velocità diverse.
OSSERVAZIONE,
DENSITA’ DI CORRENTE ELETTRICA E CAMPO ELETTRICO. Si vuole far presente che,
in base alla sua definizione, il vettore densità di corrente elettrica ha sempre verso concorde a quello
del campo elettrico. Questo si deve al fatto che essa è data dal prodotto della densità di carica per la
velocità delle cariche che la determinano. Per cui se le cariche sono negative la loro velocità ha
verso opposto al campo elettrico, ma il suo prodotto per la densità delle cariche negative avrà verso
concorde al campo elettrico. Allo stesso risultato si pervienen nel caso di cariche positive.
DEDUZIONE,
LEGAME TRA DENSITA’ DI CORRENTE ELETTRICA E INTENSITA’ DI CORRENTE
ELETTRICA. La corrente i t attraverso la superficie S orientata dal versore n rappresenta il
flusso della densità di corrente attraverso tale superficie, cioè
35
i t J P, t n P dS
S
DEFINIZIONE,
CONDUTTORE FILIFORME. Spesso il
moto delle cariche elettriche avviene in
volumi conduttori caratterizzati dall’avere
una dimensione geometrica (la lunghezza )
molto maggiore delle altre due (che ne
individuano lo spessore). In questo caso si
parla di conduttori filiformi.
Un conduttore filiforme è caratterizzato da
un asse curvilineo l. Fissando il verso del versore tangente dell’asse curvilineo del conduttore si
dice che si fissa il riferimento di corrente del conduttore stesso.
Le sezioni del conduttore filiforme ortogonali al suo asse curvilineo si assumono costanti.
DEDUZIONE,
INTENSITA’ DI CORRENTE E DENSITA’ DI CORRENTE PER IL CONDUTTORE
FILIFORME. Sia S la sezione del conduttore filiforme ortogonale al suo asse curvilineo (sezione
che, come detto, si assume costante). Allora il vettore densità di corrente si assume costante in
ciascuna sezione del conduttore e avente, punto per punto, medesima direzione del versore tangente
all’asse curvilineo. Si ha pertanto
i t J P, t t P dS S J P, t
S
J P , t
i t
t P
S
Nella prima espressione vale il segno positivo nel caso in cui J P, t abbia verso concorde con
quello di t P , vale il segno negativo altrimenti.
DEDUZIONE,
LEGGE DI CONTINUITA’. Il campo della densità di corrente e quello della densità di carica non
sono indipendenti l’uno dall’altro. Si ha infatti che
div J P, t
P, t J x P, t J y P, t J z P, t
P, t
t
y
z
t
x
DIMOSTRAZIONE. Consideriamo un volume Ω di superficie . La carica netta che esce da
esso nell’unità di tempo è pari alla intensità di corrente attraverso nel verso del versore normale
n orientato verso l’esterno. Detta i uscente t tale intensità di corrente si ha
iuscente t
J P, t n P dS div J P, t d
36
dove si è fatto ricorso, a terzo membro, del teorema della divergenza.
La carica contenuta, istante per istante, dal volume Ω è esprimibile attraverso la densità di carica nel
modo seguente
q int erna t
P, t d
quindi possiamo esprimere i uscente t anche nel modo seguente
d P, t d
d q int erna t
P, t d
i uscente t
t
dt
dt
Per confronto si ha pertanto
P, t
d
t
div J P, t d
Dovendo questa relazione valere per ogni possibile
volume Ω che si intenda considerare deve essere
necessariamente vero che
div J P, t
P, t
t
che è quanto volevasi dimostrare.
DEDUZIONE,
CONDIZIONI STAZIONARIE. In condizioni stazionarie il campo della densità di corrente è
solenoidale.
DIMOSTRAZIONE. Le condizioni stazionarie comportano, fra l’altro, che il campo della densità
di carica sia costante nel tempo. Ma allora la legge di continuità si scrive
div J P 0
Ricordando che un campo vettoriale è detto solenoidale quando ha divergenza nulla punto per
punto, abbiamo la tesi.
II)CAMPO ELETTRICO GENERICO E TENSIONE ELETTRICA
GENERALITA’. Nei capitoli primo e secondo si è studiato il campo elettrostatico (o
coulombiano), il campo elettrico cioè che si ha quando tutte le cariche elettriche sono ferme nello
spazio. Questo campo elettrico è l’unico presente anche nel caso in cui si abbiano condizioni
stazionarie, cioè nel caso in cui risulti costante nel tempo sia la densità di carica che la densità di
corrente.
Quando invece la densità di carica e la densità di corrente variano nel tempo le cariche libere
sperimenteranno, come vedremo, oltre al campo elettrico coulombiano, conservativo, anche una
altro campo elettrico, che chiamiamo campo elettrico indotto; quest’ultimo è non conservativo.
37
DEFINIZIONE,
CAMPO ELETTRICO GENERICO. Definiamo campo elettrico generico la somma del campo
elettrico coulombiano (o elettrostatico) e del campo elettrico indotto.
Indicando con i simboli
Ec , E i , E
rispettivamente il campo elettrico coulombiano, quello indotto, e il campo elettrico generico,
somma dei primi due, possiamo riassumere ciò che si verifica nella condizione elttrostatica, nella
condizione stazionaria e nella condizione generica, nella tabella successiva.
STAZIONARIETA’
ELETTROSTATICA
Non ci sono variazioni
Le cariche elettriche
nel tempo delle
sono ferme nello spazio
grandezze elettriche
E P E c P
P
0
t
E P E c P
J P 0
E P , t E c P , t E i P , t
P
0
t
P, t
0
t
J P, t
0
t
P, t
div J P, t
t
CONDIZIONE
GENERICA
Le grandezze elettriche
variano nel tempo
J P
0
t
div J P 0
DEFINIZIONE,
TENSIONE ELETTRICA. Definiamo tensione elettrica l’integrale di linea del campo elettrico
generico lungo la linea l orientata dal versore tangente t . Poniamo
ut E P, t t dl
l
A parità di campo elettrico la tensione elettrica dipende dalla linea l e dalla sua orientazione. In
particolare invertendo l’orientazione di l (cioè cambiando verso al versore tangente t ) la tensione
cambia il proprio segno.
Nel caso la linea l sia aperta, di estremi A e B e
orientata da A a B, allora si scrive
B
u AB t E P, t t dl
A,l
I pedici ordinati A e B in u AB t specificano che
la linea l è orientata da A a B.
In genere si usa mettere un + in corrispondenza
del punto di inizio della linea (il punto A) ed un meno nel punto finale (il punto B). Si può anche
trovare una freccia che vada dall’estremo finale all’estremo iniziale.
38
Questi tre sistemi sono equivalentemente usati per indicare l’orientazione che si è assunta per la
curva l, nel calcolo della tensione lungo di essa.
Al pari del potenziale elettrico la tnsione ha dimensione di Volt (V), unità di misura omogenea a
joule su coulomb (J/C).
DEDUZIONE,
SIGNIFICATO DELLA TENSIONE ELETTRICA. La tensione elettrica u AB t è il lavoro
realizzato dal campo di forze elettromagnetiche per portare una carica dal punto A al punto B,
diviso il valore della carica.
DEDUZIONE,
TENSIONE ELETTRICA E DIFFERENZA DI POTENZIALE. Nel caso in cui il campo
elettrico generico sia esclusivamente coulombiano (cioè certamente in condizioni elettrostatiche e in
condizioni stazionarie) risulta
u AB t V A, t V B, t
DIMOSTRAZIONE. Nel caso in cui il campo elettrico si tutto coulombiano si ha
ut E c P, t t dl V B, t V A, t V A, t V B, t
l
essendo E c P, t un campo conservativo di primitiva V P, t .
OSSERVAZIONE,
DIFFERENZA DI POTENZIALE. Nel calcolo della tensione fra due punti A e B, nel caso di
campo elettrico esclusivamente coulombiano, si possono avere le seguenti possibilità.
1)Se V(A)>V(B) allora il campo elettrico è mediamente diretto da A verso B.
2)Se V(A)<V(B) allora il campo elettrico è mediamente diretto da B verso A.
3)Se V(A)=V(B) allora non c’è moto macroscopico di carica fra A e B. Questo può accadere ad
esempio fra due punti della superficie di un conduttore in condizioni elettrostatiche.
Poiché il potenziale di un punto all’infinito è pari a zero, il potenziale V(P) del punto P si deve
vedere come la differenza di potenziale fra il punto P ed un punto all’infinito. Cioè come il lavoro
necessario per portare una carica dal punto P all’infinito, diviso la carica stessa.
III)LEGGI DI OHM E DI JOULE
INTRODUZIONE. Nel seguito viene considerata la corrente elettrica di conduzione descritta dal
campo J P, t che si manifesta nei materiali per effetto del campo elettrico E P, t . Per semplicità
di trattazione conviene considerare il caso di condizioni stazionarie nelle quali, lo ricordiamo, si ha
div J P 0
E P E c P V P
cioè il campo della densità di corrente è solenoidale e il campo elettrico è tutto coulombiano,
dunque conservativo.
39
OSSERVAZIONE SPERIMENTALE,
ESPERIENZA DI OHM E LEGGE DI
OHM. L’esperienza di Ohm si basa
sull’apparato sperimentale indicato in
figura. L’amperometro ed il voltmetro
permettono di valutare i valori di tensione
U e intensità di corrente I (abbiamo detto
di porci in condizioni stazionarie) e di
verificare che il loro rapporto risulta
costante. Tale costante è detta resistenza e
dipende dal materiale che costituisce il
cilindro e daale sue dimensioni, come sarà
meglio illustrato nel seguito.
Si pone dunque
R
U
I
La resistenza ha la dimensione fisica di ohm (Ω), quantità omogenea a volt su ampere V/A. Il
reciproco della resistenza è detta conduttanza. Si pone
G
I
U
La conduttanza ha la dimensione fisica di siemens (S), quantità omogenea ad ampere su volt (A/V).
OSSERVAZIONE SPERIMENTALE,
EFFETTO JOULE. L’esperienza di Joule si basa sull’apparato sperimentale già introdotto per
l’esperienza di Ohm. Essa prova che il tratto cilindrico lungo l, avente resistenza R e percorso dalla
corrente costante I si riscalda, dissipando la potenza
Pd RI 2 UI
OSSERVAZIONE SPERIMENTALE,
RESISTENZA, PARAMETRI GEOMETRICI E MATERIALE. Come si diceva sopra la
resistenza del cilindro usato nelle esperienze di Ohm e di Joule dipende dalle dimensioni del
cilindro (cioè da S e da l), oltre che dal tipo di materiale di cui esso è fatto.
In particolare si trova che vale la seguente relazione
R
l
S
dove ρ è detta resistività ed è un parametro che varia da materiale a materiale. Essa ha la
dimensione di ohm per metro (Ωm). Il suo reciproco è detto conducibilità e si indica γ. La
conducibilità ha la dimensione di siemens su metro (S/m) e soddisfa la relazione
G
S
l
40
OSSERVAZIONE SPERIMENTALE,
LA RESISTIVITA’. La resistività dei materiali è sensibile alla temperatura a cui gli stessi si
trovano. Sperimentalmente si trova che la resisitvità, in prossimità dei 20°C (temperatura
ambiente), cresce linearmente con la temperatura secondo la legge lineare
t t 20C 1 t 20C
dove t è la temperatura in gradi centigradi e α è una costante del materiale, detta coefficiente di
temperatura.
Nella tabella che segue si riporta sia la resistività a 20°C che il coefficiente di temperatura per tre
metalli. Come si vede, il ferro non è il metallo a resistività minore. Questo è infatti l’argento. Ma il
suo costo elevato fa preferire il rame come materiale conduttore per gli usi ordinari.
RESISTIVITA’ E COEFFICIENTE DI TEMPERATURA A 20°C
t 20C
Metallo
8
Argento
1.47 10 m
0.0038 C 1
Rame
1.72 10 8 m
0.00393 C 1
Ferro
10 10 8 m
0.0050 C 1
Si osserva che il materiale a resistività minore è anche quello con il coefficiente di temperatura più
basso, cioè è anche quello la cui resistività cresce di meno all’aumento di temperatura. Si veda
ancora il caso del ferro. Esso è meno adatto, per esempio del rame, come conduttore, sia perché la
sua resistività, a temperatura ambiente, è più alta; sia perché la sua resistività cresce più
velocemente al crescere della temperatura.
OSSERVAZIONE SPERIMENTALE,
LEGGE DI OHM IN PICCOLO. La legge di Ohm suggerisce una relazione che coinvolge i
valori puntuali di resistività, campo elettrico generico e densità di corrente. Questa relazione molto
importante prende il nome di relazione costitutiva del campo di corrente, o legge di Ohm alle
grandezze specifiche, o anche legge di Ohm in piccolo. Essa si scrive
E
c P , t E i P , t P J P , t E P , t P J P , t
La validità di questa legge risulta verificata sperimentalmente nel senso che la sua integrazione nei
casi particolari fornisce risultati conformi alla realtà.
Si osserva che la validità della legge di Ohm in piccolo non è
ristretta al caso stazionario.
OSSERVAZIONE,
LEGGE DI OHM E POSTULATO DI FOURIER. Qui si
vuole discutere l’analogia tra la legge di Ohm in piccolo e il
postulato di Fourier della trasmissione del calore.
Ricordiamo che il postulato di Fourier si scrive
dQ n
T P, t
dAdt
n
dove i simboli hanno il significato seguente:
41
1)dA è una superficie infinitesima centrata nel punto generico P;
2)dt è l’intervallo infinitesimo di tempo;
3)λ è una costante dipendente fondamentalmente dal materiale detta conduttività termica;
4)T(P,t) è la temperatura nel punto P all’istante T;
4) dQn è la quantità di calore che transita attraverso dA, nel tempo dt, nella direzione e nel verso
individuati dal versore n .
Ora quanto vale la quantità di carica che transita attraverso dA, nel tempo dt, nella direzione e nel
verso individuati dal versore n ? Supponendo di avere cariche di un solo segno, per semplificare la
notazione, tale quantità sarà
P
,
t
v
P
,
t
dtdA
densità
n
dove si è specificato il significato di ρ in quanto tra breve tale simbolo comparirà anche come
resistività (che pasticcio!). Ma, ricordando la definizione di densità di corrente, tale quantità si
scrive
J
P
,
t
dtdA
n
J
P
,
t
n dtdA
Ora, in base alla legge di Ohm in piccolo, tale quantità vale
J P, t n dAdt
1
resistività
E P, t E P, t
c
n dAdt
i
Nel caso poi che il campo elettrico sia conservativo (come ad esempio nella condizione stazionaria)
allora si ha
J P, t n dAdt
1
resistività
E P, t n dAdt
1
resistività
V P, t n dAdt
1
resistività
V P, t
dAdt
n
Introducendo il reciproco della resistività, cioè la conduttività del materiale, la legge di Ohm in
piccolo nel caso di campi elettrici conservativi è
J P, t n dAdt
V P, t
dAdt
n
formalmente identica al postulato di Fourier ed anche concettualmente identica allo stesso,
specialmente se nella trattazione della trasmissione del calore si introducesse un vettore analogo al
vettore J il quale fosse definito come segue
Q P, t =(densità di calore in P all’istante t)x(velocità di spostamento del calore)
il cui potenziale risulterebbe la temperatura, cioè per il quale varrebbe la relazione
42
Q P , t T P , t
DEDUZIONE,
POTENZIALE IN CONDIZIONI STAZIONARIE. Consideriamo ora soli fenomeni stazioanari.
In questo caso la legge di continuità si scrive
div J P, t 0
La legge di Ohm in piccolo si scrive invece
J P, t E c P, t V P, t
in quanto il campo elettrico è di natura esclusivamente coulombiana.
Pertanto, sostituendo la seconda equazione nella prima si ha
div V P, t 0
Se assumiamo che la conduttività del materiale sia la stessa in ogni suo punto si ha infine
2V P, t 0
Dunque anche nel caso in cui le cariche non stiano ferme nello spazio, ma si muovano dando luogo
ad un campo di densità di corrente costante nel tempo, ovvero ad una densità di carica costante nel
tempo, il potenziale elttrico deve soddisfare sempre alla equazione di Laplace.
DEDUZIONE,
CAMPO ELETTRICO IN CONDIZIONI STAZIONARIE. Per il campo elettrico in condizioni
stazionarie si scopre una interessante proprietà. Esso intanto è tutto coloumbiano, essendo nullo il
campo elettrico indotto. Abbiamo dunque un campo coulombiano non nullo all’interno di un
conduttore. E questa è una bella novità rispetto all’elettrostatica. L’altra novità è che questo campo
risulta solenoidale, cioè a divergenza nulla. Infatti la legge di Ohm in piccolo si scrive
J P E c P
e la legge di continuità si scrive
P
div J P
0
t
per cui sostituendo la prima equazione nella seconda si ha
div E c P 0 div E c P 0
dove si è assunta costante la conduttività del materiale.
43
Certo, anche nella elettrostatica, all’interno di un conduttore, il campo elettrico era solenoidale. Ma
questo perche era nullo identicamente. Qui è invece non nullo e solenoidale.
Si osservi che la solenoidalità del campo elettrico coulombiano all’interno di conduttori attraversati
da corrente stazionaria non è in contraddizione con la leffe di Gauss. Infatti la densità di carica netta
all’interno del conduttore continua ad essere nulla anche quando questo è percorso da corrente
stazionaria.
DEDUZIONE,
LEGGE DI JOULE IN PICCOLO. Anche la legge di Joule suggerisce una relazione che
coinvolge i valori puntuali di resistività e densità di corrente. Questa relazione molto importante
prende il nome di espressione della potenza specifica dissipata o di legge di Joule in piccolo.
Essa afferma che la potenza dissipata punto per punto in un conduttore avente resistività ρ è data da
pd P, t resistività J P, t
2
La dimensione fisica della potenza specifica è il watt su metro cubo (W/m^3).
La legge di Joule in piccolo ha validità generale, non è cioè limitata al caso stazionario.
IV)CONDUTTORI DI FORMA GENERICA IN CONDIZIONI
STAZIONARIE
Consideriamo un tronco di un conduttore di forma generica, circondato da materiale isolante.
Essendo J E ed essendo nulla la conduttività dell’isolante, possiamo affermare che il campo di
corrente è tutto confinato all’interno del conduttore ed il conduttore rappresenta pertanto un tronco
di tubo di flusso del vettore J .
Supponiamo ora che ci si trovi in condizioni stazionarie. In tali condizioni sappiamo allora valere le
seguenti due relazioni
1) div J P 0
2) J P, t resistività P E c P V P
In base alla prima relazione si deve affermare che, essendo il campo della densità di corrente
solenoidale, esso è conservativo del flusso. In altri
termini è possibile attribuire una intensità di corrente
al conduttore calcolandola attraverso una qualunque
superficie che tagli tutte le linee vettoriali di J
(questo genere di superficie sono dette superficie
tappo). Presa allora una superficie tappo S e detta I
l’intensità di corrente si ha
I J P ndS
S
dove n indica il versore normale della superficie S.
44
Siano ora S A ed S B due superficie tappo ortogonali punto per punto al campo di corrente J .
Essendo J E c esse sono ortogonali al campo E c e dunque sono due superficie equipotenziali.
Allora, in base alla relazione 2, possiamo assegnare al conduttore una tensione U, calcolandola
come integrale di linea del campo elettrico fra un punto qualunque della superficie S A e un punto
qualunque della superficie S B , cioè ponendo
B
U E c P t dl
A
In tal modo resta definito il rapporto costante
B
E c P t dl
U
I
A
J P ndS
S
che definiamo resistenza del nostro conduttore in condizioni stazionarie. Dunque si pone
B
R
E c P t dl
A
J P ndS
S
Si sottolinea che questa posizione è possibile solo nel caso di condizioni stazionarie, cioè nel caso
in cui sia possibile attribuire al conduttore una intensità di corrente ed una tensione.
DEDUZIONE,
POTENZA DISSIPATA NEL CONDUTTORE IN FORMA GENERICA IN CONDIZIONI
STAZIOINARIE. In condizioni stazionarie la potenza dissipata in un tronco di tubo di flusso del
vettore J è data da
Pd UI RI 2
DIMOSTRAZIONE. Si deve dimostrare che sussiste uguaglianza fra la energia dissipata valutata
attraverso la legge di Joule in piccolo
Pd pd P d
1
J P, t
2
d
dove Ω è il volume del tronco di tubo di flusso, e l’espressione indicata nella tesi, che si scrive
come il seguente prodotto di integrali
B
Pd UI E c P t dl J P ndS
A
S
45
Lascio questa dimostrazione a futuri approfondimenti.
ELETTROCINETICA
E P, t E c P, t E i P, t
Non definito non essendo il campo elettrico
conservativo
CAMPO ELETTRICO
POTENZIALE ELETTRICO
J P, t E P, t
POSTULATO DI OHM
p d P J P , t J P , t
POSTULATO DI JOULE
P, t
div J P, t
t
ELETTROCINETICA STAZIONARIA
CONSERVAZIONE DELLA CARICA
E P E c P V (P)
CAMPO ELETTRICO
E i ( P) 0
2V P, t 0
POTENZIALE ELETTRICO
V ( P) E P E c P
J P E c P V P
POSTULATO DI OHM
P
div J P
0
t
CONSERVAZIONE DELLA CARICA
POTENZA DISSIPATA DA UN TRONCO
DI TUBO DI FLUSSO DI J
p d J P J P
POSTULATO DI JOULE
B
Pd UI E c P t dl J P ndS
A
S
B
RESISTENZA DI UN TRONCO DI TUBO
DI FLUSSO DI J
R
U
I
E c P t dl
A
J P ndS
S
V) GENERATORI ELETTRICI
PREMESSA. Poiché J è, in condizioni stazionarie,
solenoidale, è possibile considerare un tronco di tubo di
flusso che si richiude su sé stesso.
Il lavoro del campo elettrico coulombiano nello
spostamento delle cariche all’interno di questo tubo di
flusso è zero, essendo il campo elettrico coulombiano
conservativo. Tuttavia, nel moto delle cariche all’interno
di tale tubo di flusso, si ha dissipazione di potenza. In
particolare la potenza dissipata sarà
2
Pd pd P d resistività J P d RI 2
46
dove Ω è il volume del tronco di tubo di flusso richiuso su sé stesso e R è la sua resistenza. Ciò
vuole dire che per mantenere un campo di corrente stazionario sarà necessaria anche la presenza di
forze non conservative.
Tali forze non conservative sono dette forze elettriche generatrici.
Rapportando la forza elettrica generatrice sulla carica sulla quale agisce si ottiene la forza elettrica
specifica che si indica
E g P , t
Un campo elettrico E g P, t può avere origine da fenomeni di natura diversa (fenomeni chimici,
meccanici…) ma il suo effetto è sempre quello di determinare una separazione di cariche.
DEFINIZIONE,
GENERATORE ELETTRICO. Un componente nel quale si realizza una separazione di cariche
ad opera di un campo E g P, t è detto generatore elettrico.
DEDUZIONE,
COMPORTAMENTO A VUOTO DEL GENERATORE ELETTRICO. Un generatore si dice
a vuoto quando non si ha corrente elettrica attraverso i morsetti. Prendiamo allora in considerazione
un generatore a vuoto. Esso determina una separazione di cariche fra i due morsetti. Tale
separazione determina un campo coulombiano E c P, t il
quale, ad equilibrio raggiunto, soddisfa la relazione
E c P, t E g P, t 0
all’interno del generatore stesso. Si sottolinea che, come
si è voluto evidenzialre nel disegno, il campo elettrico
delle forze generatrici esiste solo dentro il generatore
stesso, mentre il campo coulombiano ha le caratteristiche
consuete di estendersi in tutto lo spazio circostante.
DEFINIZIONE,
FORZA ELETTROMOTRICE DEL GENERATORE.
Consideriamo un generatore a vuoto. Consideriamo una curva l,
orientata da t , che congiunga i due morsetti del generatore.
L’orientamento di l sia quello che va dal morsetto con accumulo
di cariche negative al morsetto con accumulo di cariche positive.
Ciò posto definiamo forza elettromotrice del generatore
l’integrale
f .e.m. E g t dl
l
Si osserva che, in base alla sua definizione, la f.e.m. di un generatore rappresenta il lavoro che il
campo E g P, t fa nel portare una carica dalla zona di accumulo delle cariche negative alla zona di
accumulo delle cariche positive, diviso la carica stessa.
47
DEDUZIONE,
F.E.M. E TENSIONE A VUOTO DEL GENERATORE. Introduciamo un riferimento di
tensione sul generatore. Se definiamo morsetto positivo quello con accumulo di cariche positive e
morsetto negativo quello con accumulo di cariche negative, allora la tensione del generatore a vuoto
è pari alla sua f.e.m..
DIMOSTRAZIONE. La dimostrazione è immediata. Infatti il calcolo della tensione a vuoto del
generatore (che indichiamo u0 ), con il riferimento di tensione adottato, porge
u0 Ec t dl Ec t dl E g t dl f .e.m.
l
l
l
cioè la tesi.
DEFINIZIONE,
GENERATORE A CARICO. Un generatore è detto a
carico quando si ha corrente elettrica attraverso i suoi
morsetti .
DEDUZIONE,
COMPORTAMENTO
A
CARICO
DEL
GENERATORE. Consideriamo un generatore a carico
in cui sia introdotto il riferimento di tensione che assume
positivo il morsetto con accumulo di carica positiva e
negativo il morsetto con accumulo di carica negativa.
Supponiamo di trovarci in condizioni stazionarie. Adesso trattiamo il generatore come fosse un
conduttore generico (ed in effetti un generatore è anche un conduttore, è infatti attraversato da
cariche qualora sia a carico). Ma allora vale la trattazione già fatta per il conduttore generico, solo
che in questo caso oltre al campo coulombiano si dovrà considerare anche il campo delle forze
interne al generatore, il campo E g P, t . Allora, riprendendo la trattazione fatta sul conduttore di
forma generica in condizioni stazionarie, avremo che anche in questo caso sarà costante il rapporto
E
c P E g P t dl
J P ndS
S
E c P t dl E g P t dl
J P ndS
U f .e.m.
cos tan te
I
S
A numeratore si ha sempre il lavoro fatte dalle forze del campo elettrico per portare una carica
positiva da un estremo ad un altro del conduttore, nel verso della corrente, diviso la carica stessa. A
denominatore c’è sempre la intensità di corrente.
La tensione ha qui segno meno perché il riferimento di tensione del generatore lo si pone per
convenzione invertito rispetto a quello del conduttore.
DEFINIZIONE,
RESISTENZA INTERNA DEL GENERATORE. Analogamente alla trattazione fatta per il
conduttore di forma generica in condizioni stazionarie definiamo resistenza del generatore il
rapporto sopra trattato. Dunque si pone
48
R
E
c P E g P t dl
J P ndS
S
E c P t dl E g P t dl
J P ndS
U f .e.m.
I
S
OSSERVAZIONE SPERIMENTALE,
LEGGE DI OHM IN PICCOLO PER GENERATORI. La legge di Ohm in piccolo può essere
estesa ai generatori considerando oltre al campo coulombiano e a quello indotto, anche il campo
delle forze che si sviluppano dentro il generatore. Dunque si ha
E
c P , t E i P , t E g P , t P J P , t E P , t P J P , t
La validità di questa legge risulta verificata sperimentalmente nel senso che la sua integrazione nei
casi particolari fornisce risultati conformi alla realtà.
Si osserva che la validità della legge di Ohm in piccolo non è ristretta al caso stazionario.
DEDUZIONE,
POTENZA DISSIPATA NEL GENERATORE IN CONDIZIONI STAZIOINARIE. In
condizioni stazionarie la potenza dissipata in un tronco di tubo di flusso del vettore J in cui
risiedano forze generatrici di campo è E g P, t data da
Pd RI 2
DIMOSTRAZIONE. Questa proprietà del generatore deriva dal fatto che esso è anche un
conduttore di resistenza R. Dunque la potenza da esso dissipata è pari a quella di un conduttore di
resistenza R.
DEDUZIONE,
BILANCIO DI POTENZA PER UN GENERATORE. In un generatore a carico la potenza
generata in condizioni stazionarie si può calcolare come
Pg
dQ
d
Q E g t dl
E g t dl I E g t dl If .e.m.
dt l
l
dt l
D’altra parte il generatore disperde in calore la potenza
Pd RI 2
Dunque la potenza erogata dal generatore è
Pe Pg Pd f .e.m.I RI 2
49
VI) CIRCUITO RC SERIE
DEFINIZIONE,
CIRCUITO RC SERIE. Definiamo circuito RC serie
il circuito rappresentato in figura in cui si realizza il
collegamento in serie di un generatore di forza
elettromotrice costante f.e.m., di un resistore di
resistenza R e di un condensatore di capacità C.
DEDUZIONE,
CARICA DEL CONDENSATORE. Se le armature
del condensatore sono scariche negli istanti t 0 e
l’interrottore viene chiuso all’istante t = 0, allora la
carica sulle armature del condensatore varia nel tempo
secondo la legge
t
qt Cf .e.m.1 e RC
DIMOSTRAZIONE. Chiudiamo l’interruttore e calcoliamo la circuitazione del campo elettrico
lungo il circuito nel verso della corrente. Si ha
f .e.m. uR t uC t 0
Osservato ora che
u R t i t R
uC t
qt
C
dqt
R
dt
la circuitazione del campo elettrico si traduce nella
equazione differenziale
f .e.m.
dqt
qt
R
0
dt
C
Si tratta di una equazione differenziale a variabili separabili che si risolve nel modo seguente.
f .e.m.
dqt
qt
qt dqt
f .e.m.C qt RC
R
0 f .e.m.
R
dt
C
C
dt
dqt
dt
dqt
dt
dq
1
d f .e.m.C q
t
dt
f .e.m.C qt RC
f .e.m.C q RC 0
f .e.m.C q
RC
0
0
t
ln f .e.m.C q 0
t
t
t
t
f .e.m.C qt
t
ln
RC
f .e.m.C
RC
Mettondo ora primo e secondo membro come esponente del numero di Nepero otteniamo
50
f .e.m.C qt f .e.m.Ce
t
RC
t
qt f .e.m.C 1 e RC
Come volevasi dimostrare. L’andamento della legge temporale trovata è indicato in figura.
DEDUZIONE,
ENERGIA FORNITA AL CONDENSATORE. L’energia fornita al condensatore durante il
processo di carica è pari a
U
1 Q2
2 C
DIMOSTRAZIONE. In base al principio di conservazione dell’energia si ha che l’energia
potenziale accumulata dal condensatore deve essere pari alla energia erogata dal generatore
f .e.m. i t dt f .e.m.
0
0
dqt
dt f .e.m.qt qt 0
dt
f .e.m.qt C f .e.m.
2
Q2
C
meno l’energia dissipata in calore dalla resistenza R
2
2
2
t
f .e.m.2 RC
f .e.m.2 RC t
dqt
2
Ri
t
dt
R
dt
R
e
dt
e
dt
0
0 dt
0 R 2
R
0
Tenendo presente ora che dallo studio degli integrali impropri si ha
e
x
dx 1
0
possiamo concludere
2
Ri t dt
0
2
2
f .e.m.2 RC t
f .e.m.2 RC RC t 2 f .e.m.2 C Q 2
e
dt
0 e d RC t 2 2C
R 0
2R
Dunque al condensatore va l’energia
Q2 Q2 Q2
C 2C 2C
e la tesi è dimostrata.
VII) LE LEGGI DI KIRCHHOFF
DEDUZIONE,
51
LA PRIMA LEGGE DI KIRCHHOFF. Supponiamo di avere un circuito elettrico ramificato.
Prendiamo in considerazione un nodo di tale sistema, ovvero un punto del circuito in cui
convergono più tubi di flusso della densità di corrente. Allora la solenoidalità di J ci permette di
affermare che la somma delle correnti uscenti da una superficie chiusa S, delimitante il nodo, deve
essere nulla. Cioè
i
i
0
in cui le correnti con riferimento uscente da S vanno
sommate, vanno sottratte quelle con riferimento
entrante.
OSSERVAZIONE,
VALIDITA’ DELLA PRIMA LEGGE DI
KIRCHHOFF. La prima legge di Kirchhoff si basa
sulla solenoidaleità di J che è senz’altro garantità nelle
condizioni stazionarie (in base alla legge di conservazione della carica). In ogni altro caso tale
condizione non è in generale garantita e dunque la prima legge di K. non è, in generale, applicabile.
DEDUZIONE,
SECONDA LEGGE DI KIRCHHOFF. Si consideri una magli di un circuito elettrico, ovvero un
percorso chiuso composto da lati del circuito stesso. Fissato un verso arbitrario positivo lungo tale
maglia si ottiene una curva chiusa orientata. La circuitazione del campo elettrico totale lungo tale
percorso è data da
energia
calore energia
dissipato magnetica polarizzaz ione
E Ec Ei E g
carica
In particolare per la maglia indicata in figura si
ha
calore
dissipato
E E g carica
cioè
f .e.m.1 f .e.m. 2 i1 R1 i2 R2 i3 R3
In pratica cioè la seconda legge di Kirchhoff è
un bilancio energetico in cui si tiene conto che i tre campi elettrici presenti in un circuito realizzano
un lavoro che si trasforma o in calore o in energia magnetica (negli induttori) o in energia di
polarizzazioen (nei condensatori),
Più in generale la seconda legge di Kirchhoff si scrive
ut 0
maglia
dove la tensione va sommata se il suo riferimento è concorde al verso positivo fissato sulla maglia,
va sottratta altrimenti.
52
CAPITOLO IV,
FENOMENI MAGNETICI
VUOTO
STAZIONARI
NEL
I) GENERALITA’
Si è visto nel capitolo precedente che al trasporto di cariche in un conduttore è associato il
riscaldamento del conduttore stesso, fenomeno che è desritto quantitativamente dalla legge di Joule.
Al trasporto di carica, e quindi al movimento delle cariche, è associata anche l’esistenza del campo
magnetico, fenomeno di cui ci occuperemo in questo capitolo.
Il fatto che i fenomeni magnetici siano legati al movimento, e quindi alla velocità delle cariche,
comporta che uno stesso esperimento può apparire puramente elettrostatico in un sistema di
riferimento, mentre in un altropuò apparire sia elettrico che magnetico.
In una parola, la relatività ristretta ha un ruolo fondamentale nell’elettromagnetismo. A titolo
informativo, si può provare che le leggi che governanoi campi elettromagneticiderivano dalla
trasformazione relativistica della legge di Coulomb.
Altra conseguenza della dipendenza dei fenomeni magnetici dalla velocitàdelle cariche, di minor
rilievo intellettuale, ma di maggiore rilevanza pratica immediata, è che la sorgente del campo
magnetico è di natura vettoriale. Dunque ci si può attendere a priori che la magnetostatica sia più
complicata dal punto di vista formale di quanto lo sia l’elettrostatica, dove la sorgente dei campi, la
carica, è di natura scalare…
Va anche menzionata una caratteristica dei campi magnetici la cui giustificazione è di tipo
sperimentale: per quante ricerche si sono fatte, non è mai stato possibilemettere in luce l’esistenza
di una carica magnetica isolata, come è invece possibile fare con la carica elettrica.
Questa osservazione esprime in termini tecnici una proprietà delle calamite naturali che fa parte
dell’esperienza comune: per quanto si rompa una calamita in parti più piccole, ciascuna di queste
possiede un polo nord ed un polo sud.
La mancanza di cariche magnetiche isolate fa si che le linee di forza del campo magnetico siano
sempre chiuse, non potendo avere né origine né fine. E, su un piano più strettamente pratico, fa
anche si che non si possa definire il campo magnetico come una forza, come si è fatto per il campo
elettrico.
II) LE LEGGI DI LAPLACE
INTRODUZIONE. La magnetostatica è qui esposta in modo formalmente analogo alla
elettrostatica. Si coglierà questa analogia considerando come ‘carica magnetica’ la carica elettrica in
moto.
OSSERVAZIONE SPERIMENTALE,
FORZE MAGNETICHE. Nel vuoto la forza magnetica che la carica puntiforme q1 , avente
velocità V 1 , esercita sulla carica puntiforme q2 , avente velocità V 2 , è data da
F0 r2 q 2 V2 B0
con
53
B0
0
4
r r
2 1
q1 V1
r2 r1
2
r2 r1
dove
0 4 10 7
Wb
Am
I valori di q1 e q2 si intendono come valori algebrici. Essi possono dunque essere positivi o negativi.
B0 è il campo dell’azione magnetica il quale viene impropriamente denominato intensità di
induzione magnetica (sarebbe stato più opportuno chiamarlo campo magnetico, nome invece
attribuito ad un’altra grandezza).
Dunque tale forza può scriversi
r r
2 1
q 2 V2 q1 V1
r2 r1
F0 r2 0
2
4
r2 r1
formula che rappresenta in magnetostatica ciò che la legge di Coulomb rappresenta in elettrostatica.
OSSERVAZIONE,
QUESITO APERTO. Le forze che due cariche in moto si scambiano sembrano non essere uguali e
contrarie. Infatti le due forze sono
r r
2 1
q 2 V 2 q1 V1
r r
q
V
r
r
q
V
q
V
q
V
r
r
2 1
2
2
2
1
1
1
2
2
1
1
2
1
0
0
F0 r2
2
2
4
4
r2 r1
r2 r1
r r
2 1
q1 V1 q 2 V2
r r
q
V
r
r
q
V
q
V
q
V
r
r
2 1
1
1
2
1
2
2
1
1
2
2
2
1
0
0
F0 r1
2
2
4
4
r2 r1
r2 r1
54
r r
q
V
r
r
q
V
q
V
q
V
2 1
1
1
2
1
2
2
2
2
1
1
0
2
4
r2 r1
Si lascia ad ulteriori analisi l’interpretazione di questo fatto.
DEFINIZIONE,
PERMEABILITA’ MAGNETICA DEL VUOTO.
Definiamo permeabilità magnetica del vuoto la costante
4 10 7
Wb
A m
e lo indichiamo col simbolo 0 .
DEFINIZIONE,
UNITA’ DI MISURA DELLA INDUZIONE MAGNETICA.
L’induzione magnetica nel vuoto si misura in
metro
metro
1
sec ondo massa
massa
2
sec ondo
sec ondo
sec ondo
coulomb metro
coulomb metro
coulomb
massa
newton sec ondo
coulomb metro
massa
coulomb sec ondo
Introdotta la grandezza
volt sec ondo
weber (Wb)
metro 2
massa metro 2
.
coulomb sec ondo
newton metro
sec ondo
coulomb
metro 2
massa
metro
metro
sec ondo 2
sec ondo
coulomb
metro 2
allora l’induzione magnetica si misura in Wb
, ovvero in tesla (simbolo T ).
m2
Per fissare le idee il campo magnetico terrestre è dell’ordine di 10 5 T, mentre i più grandi campi
magnetici che l’uomo è in grado di produrre sono dell’ordine di 10T.
OSSERVAZIONE,
DUE FORMULE IN UNA.
La prima osservazione sperimentale riportata racchiude i risultati delle due linee di indagine
sperimentale che furono seguite quando si posero le basi teoriche dell’elettromagnetismo: quella
volta a determinare il campo magnetico prodotto da cariche in moto (che condusse alla prima
formula di Laplace), e quella volta alla determinazione dell’azione di campi magnetici su cariche in
moto (che condusse alla espressione della forza di Lorentz e alla seconda formula di Laplace).
55
Nel seguito riportiamo le formule in essa riunite, secondo l’esposizione classicamente riportata nei
libri di fisica.
OSSERVAZIONE SPERIMENTALE,
CAMPO MAGNETICO PRODOTTO DA UNA CARICA IN MOTO.
Una carica q che si muova nel vuoto ad una velocità V produce una induzione magnetica
B0
0
4
qV
r
r
r2
dove il vettore r ha origine nella posizione occupata dalla carica, istante per istante, e estremo
libero nel punto in cui si vuole determinare l’induzione magnetica.
Questa espressione, valida finché la velocità della carica è piccola rispetto a quella della luce,
mostra, fra l’altro, che non esiste campo magnetico nella direzione del moto della carica.
DEDUZIONE,
LA PRIMA FORMULA DI LAPLACE.
E’ la applicazione immediata della precedente formula al caso in cui si abbia a che fare con fili
percorsi da corrente. Essa ci dice che un elemento di filo percorso da corrente deteremina un campo
magnetico
dB0 0
4
i dl
r
r
r2
OSSERVAZIONE SPERIMENTALE,
FORZA DI LORENTZ. Una carica q che si muova con velocità V in un campo magnetico la cui
induzione magnetica sia B0 risulta sottoposto alla forza
F0 q V B0
detta di Lorentz.
DEDUZIONE,
FORZA SU UN FILO RETTILINEO IN CAMPO MAGNETICO UNIFORME. La forza
esercitata da un campo magnetico di induzione costante B 0 su di un filo rettilineo di lunghezza l
attraversato da una corrente i è data da
F i l B0
dove il vettore l ha il verso concorde a quello della corrente che attraversa il conduttore. Infatti, in
base a quanto detto sulla forza di Lorentz, su un generico punto del conduttore agirà una forza
56
F nSq V B0
il che significa che su tutto il conduttore agisce appunto una forza
V
V
F nSq Vl B0 nSqV l B0 i l B0 i l B0
V
V
DEDUZIONE,
SECONDA FORMULA DI LAPLACE.
La seconda formula di Laplace costituisce uno strumento per il calcolo della forza magnetica agente
su un filo attraversato da corrente di forma qualsiasi inserito in un campo magnetico non uniforme.
Essa afferma che la forza agente su un tratto elementare di tale conduttore vale
d F i dl B0
Questa formula si desume in modo ovvio da quella calcolata nel caso precedente.
FORZA MAGNETICA FRA CARICHE IN MOTO
r r
2 1
q 2 V2 q1 V1
r2 r1
F0 r2 0
2
4
r2 r1
CAMPO DI UNA CARICA IN MOTO
V r
B0 0 q 3
4
r
PRIMA FORMULA DI LAPLACE
dB0
0 dl r
i 3
4
r
FORZA DI LORENTZ
F0 q V B 0
SECONDA FORMULA DI LAPLACE
d F0 i dl B 0
III) ALCUNI CASI NOTEVOLI
DEDUZIONE,
INTRODUZIONE MATEMATICA. Nei calcoli successivi capiterà più volte un integrale
apparentemente ostico il quale tuttavia si risolve facilmente con una particolare sostituzione. In
questo paragrafo si illustra il metodo risolutivo di tale integrale.
Si consideri la primitiva
dx
a
x 2 2
3
2
a0
x0
57
Operando la sosotituzione
a2 x2
a2 x2
a2
a2
a2
a
2
2
2
2
t
t
1
t
1
x
x
2
2
2
2
2
x
x
x
x
t 1
t2 1
at
dx
dt
3
2
t 12
t
la primitiva si scrive
dx
a
x
3
2 2
at
3
a
12 a 2 2
t 1
1 1
1
2 c 2 c
a t
ta
2
t
2
2
dt c
3
2
t
3
t
a 2 t 2 12 2
t 1
2
3
2
dt c
1
a2
1
t
2
dt c
Ritornando alla originale variabile si ha infine
dx
a
x
2
3
2 2
x
c
a2 a2 x2
DEDUZIONE,
L’INDUZIONE DI UN FILO RETTILINEO INFINITO. LEGGE DI BIOT-SAVART.
Consideriamo il filo infinito indicato in figura. Sia percorso da corrente i che scorra nel verso delle
z positive. Il campo di induzione magnetica da esso determinato si calcola con la prima formula di
Laplace. Si ha
d l 0 0 dz
dl r 0
r 0 OP z
0
e1
e2
e3
0
OP
dz OPdz 0 0
z
i dl r 0 i OPdz 0 0
d B 0 P 0
B0 x P 0 iOP
3
3
4 r
4
4
2 2
2
0
2iOP
4
0
z
dz
2
OP
z
OP
z
dz
2
OP
3
2 2
3
2 2
L’integrale che si ottiene è del tipo visto nel paragrafo precedente. Dunque si ha
OP
dx
2
z
3
2 2
OP
2
z
2
OP z 2
c
0
OP
dx
2
z
3
2 2
z
OP
2
2
OP z 2
0
1
OP
2
In definitiva abbiamo
58
B0 x P 0 2iOP
4
0
z
dz
2
OP
3
2 2
0
i
1
2iOP
0
2
4
2 OP
OP
Dunque si è trovato che l’induzione
magnetica nel punto P vale
0i
B 0 P
2 OP
0 0
Cioè l’induzione magnetica determinata
dalla corrente che scorre su un fili
rettilineoè un campo vettoria circolare con
asse coincidente con il filo stesso. La
corrente ‘vede’ l’induzione magnetiac
indicare la direzione antioraria.
Per fissare le idee, se immaginiamo che il filo sia percorso da una corrente di 10A, è facile
verificare che ad una distanza di 2 cm B vale 10 4 T .
Si può inoltre notare che B cala con l’inverso della distanza, invece che con l’inverso del quadrato.
Questo è dovuto al fatto che si tratta di una distribuzione di corrente infinita.
DEDUZIONE,
FORZA MAGNETICA FRA DUE FILI INFINITI PARALLELI. Due fili infiniti paralleli siano
percorsi da due correnti stazionarie. Sia d la distanza fra essi.
Qual è la forza che il primo filo esercita sul secondo? In base alla seconda formula di Laplace si ha
d F02 i2 dl 2 B 01 i2 dl 2 B01 e1 i2 dl 2
0 i1
e1
2d
E la forza che il secondo filo esercita sul primo
quanto vale?
Applicando di nuovo la seconda formula di
Laplace si ha
d F01 i1 dl1 B 02 i1 dl1 B02 e1 i1 dl1
0 i2
e1
2d
Le due forze hanno stesso modulo per unità di
lunghezza. Inoltre sono attrattive se le correnti
sono concordi, repulsive in caso contrario.
Per fissare le idee, se i due fili sono percorsi da
una corrente di 100° e distano 1cm uno dall’altro, allora la forza magnetica per unità di lunghezza
che esercitano uno sull’altro è di 0.2N/m.
DEDUZIONE,
DEFINIZIONE DI AMPERE. L’ampére viene definito come quella corrente costante che
passando in due lunghi e sottili conduttori paralleli disposti ad una distanza di 1 m nel vuoto
produce su ciascuno di essi una forza, per metro di lunghezza, pari a
59
F01 0 i1i 2 0
4 10 7
e1
N e1
N e1 2 10 7 N e1
L
2d
2
2
DEDUZIONE,
INDUZIONE SULL’ASSE DI UNA SPIRA CIRCOLARE. La prima formula di Laplace per
questa distribuzione di corrente, in un punto dell’asse z, si scrive
dl r
dB0 z 0 i 3
4
r
R sin d R cos
R cos d R sin
0
i
4
0
R
z 2 2
3
2
0
i
4
z
e1
R sin d
R cos
R
e2
R cos d
R sin
2
z
e3
0
z
3
2 2
0 Rz cos d Rz sin d R 2 d
i
3
4
2
2 2
R
z
Integrando su tutta la spira si ha
2
Rz cos d
0 0
B 0 z
i
4
2
2
2
R
d
0 0 2R 2
0 iR 2
0
0
0i
0 0
3
3
3
4
2
2 2
2
2 2
R z
R z
2R 2 z 2 2
i .
Si vede che l’induzione è massima al centro della spira (z=0) dove vale 0
2R
Per z R una stima della induzione della spira sull’asse della stessa è data da
Rz sin d
0 iR 2
B 0 z 0 0
3
2
z
Nella sezione sul dipolo magnetico si troverà una analisi approfondita del comportamento della
spira piana generica, definita anche dipolo magnetico.
DEDUZIONE,
INDUZIONE SULL’ASSE DI UN SOLENOIDE RETTILINEO. Consideriamo un solenoide
avente le caratteristiche seguenti
1)lunghezza L,
60
2)sezione circolare,
3)raggio della sezione pari ad R,
4)numero di spire pari ad N.
Vogliamo calcolare il campo di induzione
magnetica in un punto generico del suo asse.
A tale scopo introduciamo i due assi
cartesiani rappresentati in figura, coincidenti
con l’asse del solenoide.
L’asse delle x individua la posizione del punto P, punto nel quale si intende valutare l’induzione
magnetica.
L’asse delle ξ individua la posizione del punto Q, centro della spira elementare attraversata dalla
corrente
Ni
d
L
la quale determina
elementare
dB0 P
in
P
l’induzione
Ni 2
d R
L
0
2R 2 2 2
x, L x
3
Dunque l’induzione nel punto P è data da
B 0 P
L x
x
Ni 2
d R
0 NiR 2
L
3
2L
2
2 2
2R
0
L x
x
1
R
2
3
2 2
d
Di nuovo incontriamo l’integrale studiato nel paragrafo introduttivo di questa sezione. In base va
quanto visto si ha allora
B 0 P
0 NiR 2
0 Ni
2L
L x
x
1
R
2
Lx
2 L R 2 L x 2
3
2 2
d
0 NiR 2
2L
R2 R2 2
L x
x
2
2
R x
x
Dunque, per esempio, l’induzione nel punto medio dell’asse del solenoide vale
61
L
Ni
L
2
B0 x 0
2
2
2L
L
R 2
4
0 Ni
1
0 Ni
2
L2
L2
4 R 2 L2
2
R2
R
4
4
L
2
mentre quella ad una estremità del solenoide vale
B0 x 0
0 Ni
2 R 2 L2
DEDUZIONE,
INDUZIONE SULL’ASSE DI UN SOLENOIDE TOROIDALE. Un solenoide toroidale si può
pensare come un solenoide rettilineo richiuso su sé stesso in modo da formare un toro.
In genere per dare una stima della induzione sull’asse di questo genere di sistema si considera il
valore che l’induzione assume nel punto medio dell’asse di un solenoide rettilineo di lunghezza pari
alla circonferenza descritta dall’asse del toro stesso.
Pertanto se
1)r è il raggio delle spire del solenoide toroidale,
2)R è il raggio della circonferenza descritta dall’asse del solenoide toroidale,
allora in un punto qualunque dell’asse del solenoide toroidale vale
B0
0 Ni
4r 2 2R
2
0 Ni
4r 2 4 2 R 2
0 Ni
2 r2 2R2
IV) IL POTENZIALE VETTORE
OSSERVAZIONE,
POTENZIALE DELLA INDUZIONE MAGNETICA. Abbiamo visto che l’induzione magnetica
in generale non è un campo conservativo. Per questo essa, in generale, a differenza del campo
elettrico, non ammette una funzione potenziale. Più precisamente, la terza equazione di Maxwell ci
dice che l’induzione magnetica è conservativa solo nei punti dello spazio in cui la densità di
corrente è nulla. Ciò si traduce nel fatto che le circuitazioni della induzione magnetica si annullano
solo lungo quei percorsi chiusi che non si concatenano con i circuiti che generano l’induzione
magnetica stessa.
Nonostante ciò i fisici hanno voluto cercare comunque una funzione che avesse per l’induzione
magnetica un po’ il ruolo che il potenziale elettrostatico ha per il campo elettrico, ovvero una
funzione che potesse ricavarsi dalla distribuzione delle densità di corrente e dalla quale si potesse
ottenere, attraverso operazioni vettoriali, l’induzione magnetica.
DEFINIZIONE,
POTENZIALE VETTORE. Si definisce potenziale vettore della induzione magnetica la funzione
vettoriale definita dalla relazione
rot A0 x, y, z B0 x, y, z
62
e dalla condizione di solenoidaleità
div A0 x, y , z 0
OSSERVAZIONE,
FUNZIONE VETTORIALE CONSERVATIVA ARBITRARIA. Si noti che in base alla
definizione il potenziale vettore è definito a meno di una funzione vettoriale conservativa arbitraria
o, se si vuole, a meno del gradiente di una funzione scalare u arbitraria, infatti
rot A0 x, y, z u x, y, z rot A0 x, y, z rot u x, y, z rot A0 x, y, z
OSSERVAZIONE,
POTENZIALE VETTORE E TERZA EQUAZIONE DI MAXWELL. Ricordando che la
divergenza del rotore dà sempre zero si verifica che qualunque sia il vettore A esso siddisfa sempre
alla terza equazione di Maxwell.
DEDUZIONE,
EQUAZIONE DI POISSON PER IL POTENZIALE VETTORE. Per il potenziale vettore vale
la relazione
2 A0 x, y , z 0 J x, y , z
DIMOSTRAZIONE. Osservato che dalla terza equazione di Maxwell non si ricava nessuna
informazione su A, passiamo a considerare la quarta equazione di Maxwell. Imponiamo dunque che
il potenziale vettore soddisfi alla quarta equazione di Maxwell.
rot rot A0 x, y , z rot B0 x, y , z rot rot A 0 x, y , z 0 J x, y , z
div A0 x, y , z 2 A 0 x, y , z 0 J x, y , z
Se ora imponiamo alla funzione vettroiale A di essere solenoidale avremo proprio la tesi.
DEDUZIONE,
SOLUZIONE DELLA EQUAZIONE DI POISSON PER IL POTENZIALE VETTORE.
Sappiamo che, nel caso del potenziale elettrostatico, la soluzione della equazione di Poisson
2V0 x, y , z
x, y , z
0
è data dalla funzioone
V0 x, y , z
1
4 0
, ,
r
ddd
63
come risulta dalla trattazione fatta nei paragrafi sul campo elettrico ed il suo potenziale. Questo
risultato ovviamente può essere generalizzato. In particolare si può affermare che la soluzione della
equazione di Poisson per il potenziale vettore è la funzione vettoriale
J x , ,
ddd
r
0 J y , ,
A 0 x, y , z
ddd
4
r
J z , ,
ddd
r
Si ricorda sempre che r indica la distanza fra l’elemento di volume considerato nella integrazione ed
il punto in cui si calcola la funzione potenziale.
V) IL DIPOLO MAGNETICO
INTRODUZIONE. In quanto segue esamineremo in modo dettagliato le proprietà di una generica
spira piana, detta dipolo magnteico. In particolare si affronterà lo studio di spire di cui interessa il
comportamento ad una distanza tale che il loro diametro risulti trascurabile rispetto ad essa.
Si avvisa che questo studio è analogo a quello fatto per il dipolo elettrico.
DEFINIZIONE,
SPIRA PERCORSA DA CORRENTE OVVERO DIPOLO MAGNETICO. Definiamo tale un
anello piano costituito da un conduttore filiforme attraversato da corrente. Sia i la corrente che lo
attraversa ed S la superficie descritta dall’anello
DEFINIZIONE,
MOMENTO MAGNETICO DELLA SPIRA PERCORSA DA CORRENTE. Definiamo
momento magnetico della spira il vettore
m iS n
dove il versore n è quel versore ortogonale al piano
della spira è con verso tale da ‘vedere’ la corrente i
scorrere in senso antiorario.
DEDUZIONE,
POTENZIALE VETTORE DI UNA SPIRA
CIRCOLARE A GRANDE DISTANZA DA ESSA.
Consideriamo una spira circolare avente le seguenti
caratteristiche:
1)raggio δ;
2)sezione trasversale S;
3)corrente i JS .
Osservato che il vettore densità di corrente si scrive
64
J Q J Q |
i
sin
S
i
sin
S
cos
cos
0
0
il potenziale vettore della spira circolare percorsa da corrente, nel puno P, è dato da
A 0 P 0
4
2
S 2 J Q
S J Q J Q |
dl 0
d 0
d
|
4 0 QP
4 0 QP
QP
Q
P
J Q S
0
0 S J Q J Q
0 S Q | P J Q QP J Q
d
d
|
|
4 0 QP
4 0
Q
P
QP
Q
P
0 S J Q
Q | P QP d
4 0 QP Q | P
Se tuttavia diciamo che il punto P sia molto distante dalla spira, rispetto al raggio della spira stessa,
siamo autorazzitati a fare l’approssimazione
QPQ | P OP
2
che ci porta a scrivere
A0 P
4 OP
J Q Q P QP d
0 S
2
|
0
Azzardiamo inoltre un’ulteriore approssimazione e cioè
Q | P QP 2 cos
Osservato, per quanto riguarda l’angolo α, che
|
OP OQ OP cos
|
x cos y sin
OP
OQ
x cos
cos
OP
OP
OP OQ | y sin x cos y sin
z
0
Dunque si ha
Q | P QP 2 cos
2
OP
x cos y sin
e il nostro potenziale vettore, in via approssimata, si scrive
65
sin
A 0 P
J Q x cos y sin d
cos x cos y sin d
3
3
4 OP 0
4 OP 0 0
0 S 2 2
0 i 2 2
x sin d sin y sin 2 d
0
0
x sin cos y sin 2
2
0 i 2 2
i
2
2
2
0
x
cos
y
sin
cos
d
x
cos
d
y
sin
d
sin
3
3
4 OP 0
4 OP
0
0
0
0
y sin 2 d
0
2
0 i 2
0 i 2 2
2
x cos d
3
3
4 OP
4 OP
0
0
sin cos
y
2
0
x sin cos
2
0
0
2
0 i 2
3
4 OP
y
2
x
2
0
y
x
3
4 OP 0
0 i 2
Ricordando poi la definizione di momento magnetico della spira possiamo scrivere in fine
y
m
A 0 P 0
x
4 OP 3
0
Osservato ora che
i
m OP 0
x
j
k
y
0 m m x
0
y z
si può scrivere il potenziale vettore come
m OP
A 0 P 0
4 OP 3
DEDUZIONE,
CALCOLO DELLA INDUZIONE MAGNETICA DI UNA SPIRA CIRCOLARE A
GRANDE DISTANZA DALLA SPIRA STESSA. Procediamo ora al calcolo della induzione
della spira circolare percorsa da corrente a partire dal suo potenziale vettore.
66
y
0
1
0 m
B 0 P rot A 0 P rot
x
mrot
3
3
4 OP
4
2
2
2 2
x
y
z
0
0
m
4
x
2
i
x
y
j
y
x
y z
2
3
2 2
x
2
y z
2
y
x
0
k
z
3
2 2
0
x
x
y
y
3 3 3 3
r
r
r
r
0 m i j k
4
z
z
y
x
dove si è introdotto il simbolo r per la distanza OP. Calcoliamo ora le quattro derivate parziali.
x
3
x 2 y 2 z 2 2
z
y
3
x 2 y 2 z 2 2
z
x
3
x 2 y 2 z 2 2
x
3 2
3 x x 2 y 2 z 2 2 2 2 z 3xz
2
r5
3 yz
r5
3 2
1
3
1 3x 2
2
2
2 22
x
x
y
z
2
x
5
3
2
r3
r
2
2
2 2
x y z
y
3
x 2 y 2 z 2 2
y
2
1 3y
r3
r5
Dunque si ha
B 0 P
0 3xy 3 yz 2 3x 2 y 2 0 3xy 3 yz 3z 2 r 2
m
i 5 j 3
k 4 m 5 i 5 j
4 r 5
r
r5
r
r5
r
r
k
Si constata dunque la identità formale fra induzione del dipolo magnetico e campo elettrico del
dipolo elettrico.
L’espressione vettoriale della induzione magnetica è in fine
67
1 3 r m 1
B 0 P
r 3 m
4 0 r 5
r
Si può osservare come il valore che questa espressione approssimata fornisce sui punti dell’asse
della spira, cioè dell’asse z, coincidono con il valore fornito dal calcolo rigoroso fatto più sopra nel
caso della spira circolare.
DEDUZIONE,
POTENZIALE SCALARE DELLA SPIRA A GRANDE DISTANZA DA ESSA. Si può
verificare che il potenziale scalare della induzione della spira circolare è
U 0 P
0
m r
4
DEDUZIONE,
FORZA RISULTANTE AGENTE SU UNA SPIRA IMMERSA IN UNA INDUZIONE
MAGNETICA ESTERNA UNIFORME. Consideriamo il caso della spira immersa in una
induzione magnetica uniforme. La spira sia piana ma non necessariamente circolare. Diciamo che
essa sia descritta dalla curva chiusa
x cos
: y sin
z 0
0,2
Vogliamo dimostrare che la forza risultante della sollecitazione agente sualla spira immersa in una
induzione magnetica costante è nulla.
In base alla seconda formula di Laplace abbiamo allora che la forza risultante della sollecitazione
agente sulla spira è data da
x '
2
2
x ' y '
2
B0 x
'
y
B0 y x ' 2 y ' 2 d
F i dl B 0 i dl B 0 i B 0 dl i
2
2
x ' y ' B
0
0z
0
'
'
'
x B0 x
x B0 x
y B0 z
2
2
2
i y ' B0 y d i y ' B0 y d i
x ' B 0 z
d
'
0
0
0 '
0 B0 z
0 B0 z
x B 0 y y B0 x
68
2
B0 z y ' d
0
2
i
B x ' d
0z 0
2
2
B0 y x ' d B0 x y ' d
0
0
Considerando poi che
x ' ' cos sin
y ' ' sin cos
si ottiene
2
2
B0 z ' sin d cos d
0
0
2
F i
B x ' d
0z 0
2
2
2
2
B ' cos d sin d B ' sin d cos d
0x
0
0
0y
0
0
Riporto il calcolo della prima componente della risultante.
2
2
2
2
'
sin d sin d sin d 0 d sin cos d
0
2
0
2
2
0
0
2
2
B0 z ' sin d cos d B0 z cos d cos d 0
0
0
0
0
Le altre due componenti si calcolano in modo analogo e si trovano anch’esse nulle.
DEDUZIONE,
MOMENTO RISULTANTE AGENTE SU UNA SPIRA IMMERSA IN UNA INDUZIONE
MAGNETICA ESTERNA UNIFORME. Calcoliamo il momento risultante rispetto al centro
della spira, cioè al punto O. Il momento elementare è dato da
d O OQ d F Q OQ i dl Q B 0 i OQ B 0 dl OQ dl B 0
i x B0 x y B0 y dl x x ' y y ' d B 0
x '
B0 x
'
'
'
i x B0 x y B0 y y x x y y B0 y d
0
B
0z
69
x x ' B0 x y x ' B0 y
B0 x
'
'
'
'
i x y B0 x y y B0 y x x y y B0 y d
B
0
0z
Il momento risultante è dunque
2
2
B0 x x x ' d B0 y y x ' d
0
0
B0 x
2
2
2
2
O i B0 x x y ' d B0 y y y ' d x x ' d y y ' d B0 y
0
0
0
0
B
0z
0
Per il primo integrale in alto a sinistra si ha, ricordando che la spira è chiusa, quanto segue
x
0 x x d 0 x dx 2
2
2
2 2
0.
'
0
Per il secondo integrale in alto a sinistra si ha
2
2
y x d sin cos sin d
'
'
0
0
2
2
2
2
' sin cos d sin 2 sin cos d sin 2
2
0
2
0
0
0
2
I sin 2
2
0
Per l’integrale I si ha
I sin cos
2
2
0
2
d sin cos
0
2
0 ' sin cos cos 2 sin 2 d
0
2
2
' sin cos d 1 2 sin 2 d
2
0
0
2
2
2
2
1
2
2
I d 2 sin d I d sin 2 d
2 0
0
0
0
2
2
2
e dunque, tornando all’integrale di partenza, si ha
70
2
2
2
2
1
2
2
2
2
2
0 y x d 2 0 d 0 sin d 0 sin d
'
2
1
2 d S
2 0
dove S indica l’area della spira (si ricordi la formula per il calcolo del settore circolare).
Abbiamo trovato così che
2
B0 x x x d B0 y
'
0
2
y x d SB
'
0y
0
In modo analogo si prova che
2
B0 x x y ' d B0 y
0
2
y y d SB
'
0x
0
Essendo poi
x
0 x x d 0 x dx 2
2
2
2 2
0
'
2
2
y y d y dy
'
0
0
y
2
0
2 2
0
0
Si conclude che
B0 y
0 B0 x
O iS B0 x iS 0 B0 y iS n B0 m B0
0
1 B
0z
OSSERVAZIONE,
SOLLECITAZIONE AGENTE SU UNA SPIRA IN UNA INDUZIONE MAGNETICA
COSTANTE. In base a quanto calcolato la sollecitazione agente su una spira piana di forma
qualsiasi, immersa in una induzione magnetica costante, risulta equivalente ad una coppia di
momento
m B 0
Si osserva l’identità formale con la situazione che si verifica nel caso del dipolo elettrico immerso
in un campo elettrico uniforme. In quel caso però è già la sollecitazione effettiva ad essere una
coppia. Qui la sollecitazione effettiva è equivalente ad una coppia.
71
VI) IL FLUSSO DELLA INDUZIONE MAGNETICA
INTRODUZIONE. Quando ci siamo dedicati al calcolo della induzione magnetica determinata dal
alcune distribuzioni notevoli di corrente, abbiamo sempre visto come le linee di forza di tale campo
abbiano la proprietà di richiudersi su sé stesse. Vogliamo qui provare che questa è una proprietà
sempre verificata dalla induzione magnetica.
Per far questo è sufficiente dimostrare che il flusso della induzione magnetica, attraverso una
qualunque superficie chiusa, è sempre nullo. Dobbiamo dunque trovare una sorta di ‘legge di Gauss
per la magnetostatica’.
DEDUZIONE,
LEGGE DI GAUSS PER LA MAGNETOSTATICA.
Una carica puntiforme nel vuoto q viaggi con velocità V all’interno di una generica superficie
chiusa Ψ. Allora il flusso della induzione magnetica attraverso Ψ è dato da
B 0 dS 0
DIMOSTRAZIONE. Calcoliamo il flusso della induzione magnetica attraverso la superficie
chiusa Ψ. A tale scopo indichiamo la generica rappresentazione parametrica di una superficie chiusa
in coordinate sferiche.
x r , sin cos
y r , sin sin
z r , cos
, D
D , 2 | 0, , 0,2
L’espressione di B 0 è data da
B0
0 V r 0 1
q 3
q
4
r
4 r 3
i
j
k
Vx
rsen cos
Vy
rsen sen
Vz
r cos
r cos V y rsen senVz
0 1
q 3 rsen cos Vz r cos V x
4 r
rsen senV x rsen cos V y
cos V y sensenVz
0 1
q 2 sen cos Vz cos V x .
4 r
sensenV x sen cos V y
Il flusso di B 0 attraverso Ψ è dunque
72
B 0 dS
cos V y sensenV z
sen cos V z cos V x
A ,
B ,
2
2
r ,
r ,
0 q
dd
4 D sensenV x sen cos V y
C ,
2
r
,
Dove A, B, C sono definite dalla relazione
y z x y z
,
,
,
A, B, C x ,
dalla quale si ricava che
y
z
r r sen r r sen cos cos r 2 sen 2 cos
z
z
B ,
z
x
r
r
2
2
x r sen cos sin r cos r sen sen
x
C ,
x
y
A ,
y
r
2
2
y r sen r sen cos
In base a ciò il flusso si scrive
B
0
dS
q0V y
4
q0Vz
4
q0Vx
4
sin sin r ,
r ,
D
cos cos r ,
dd
r ,
cos sin r , sin cos r ,
dd
r ,
r ,
D
sin r ,
dd I1 I 2 I 3
r ,
D
Per effettuare il calcolo dei tre integrali è necessario ricordare le formule di integrazione per parti
degli integrali doppi. Si ricordi dunque che
g ,
f ,
dd f , g , d
g , dd
D
D
g ,
f ,
f ,
dd f , g , d
g , dd
y
D
D
f ,
D
D
73
dove la curva D è la frontiera del dominio D a cui viene attribuito verso positivo tale da lasciare
il versore normale sempre all’esterno del dominio stesso.
Nel nostro caso la curva è quella indicata in figura.
Procediamo dunque al calcolo del primo dei tre integrali.
I1
q 0V x
4
sin sin r ,
r ,
D
r ,
q 0V x
4
r ,
D
cos cos r ,
dd
r ,
sin sin r ,
dd
q 0V x
4
D
cos cos r ,
dd
Si osservi ora che tale integrale può riscriversi come segue
I1
q 0V x
4
q V
sin cos ln r ,
dd 0 x
4
D
sin cos ln r ,
dd
D
Applicando adesso la seconda formula di integrazione per parti al primo integrale a secondo
membro si ha
sin cos ln r ,
ln r ,
dd
sin cos d
D
D
ln r ,
sin cos dd
D
ln r ,
2 ln r ,
sin
cos
d
D sin cos dd
D
Applicando invece la prima formula di integrazione per parti al secondo integrale a primo membro
si ha invece
sin cos ln r ,
ln r ,
dd
sin cos d
D
D
D
D
ln r ,
sin cos dd
2 ln r ,
sin cos dd
ln r ,
sin cos d
D
Dunque l’integrale I 1 si scrive
74
q 0V x
4
sin sin r ,
r ,
D
cos cos r ,
dd
r ,
ln r ,
2 ln r ,
sin
cos
d
sin cos dd
q V D
D
0 x
2
4
ln r ,
ln r ,
sin cos d
sin cos dd
D
D
q V ln r ,
ln r ,
0 x
sin cos d
sin cos d
4 D
D
Dove si è considerato che, in base al teorema di Schwartz, risulta
2 ln r , 2 ln r ,
Prendiamo in considerazione ora il primo dei due integrali di linea. Guardando il disegno di D
si trova che
0
ln r ,
ln r ,0
ln r ,2
sin
cos
d
sin
d
0
sin d 0
D
0
ln r ,0
ln r ,2
ln r ,0 ln r ,2
sin d
sin d
sin d
0
0
0
Ma essendo la superficie Ψ una superficie chiusa, ne segue che r,0 r,2 e duenque
l’integrale di cui sopra risulta nullo.
Per il secondo integrale di linea si perviene allo stesso risultato e dunque si conclude che I 1 0 .
L’integrale I 2 si scrive
q 0V y sin cos r ,
cos sin r ,
dd
dd
r ,
4 D
4
D
q 0V y sin sin ln r ,
q 0V y sin sin ln r ,
dd
dd
4 D
4
D
I2
q 0V y
r ,
Applicando, nell’ordine, la prima e la seconda formula di integrazione per parti si ha
q 0V y ln r ,
2 ln r ,
sin
sin
d
sin sin dd
4 D
D
2
q 0V y
ln r ,
ln r ,
sin sin d
sin sin dd
4 D
D
q 0V y ln r ,
ln r ,
sin sin d
sin sin d
4 D
D
I2
75
Anche qui si è sfruttato il teorema di Schwartz. Sviluppando ora gli integrali curvilinei si ha
I2
q 0V y ln r ,
ln r ,
sin sin d
sin sin d
4 D
D
2
0
ln r ,
ln r 0,
0
sin
sin
d
0
sin 0 sin d
q 0V y
0
2
0
4
ln
r
,
0
ln
r
,
2
sin sin 0d 0
sin sin 2d 0
0
q 0V y
0 0 0 0 0 0 0 0 0
4
Resta il calcolo del terzo integrale. Applicando la seconda formula di integrazione per parti si ha
sin
r ,
q 0V z sin r ,
q 0V z
I3
r , dd
r , dd 4 sin d
4
D
D
D
q 0V z
4
q V
sin r ,
dd 0 z
sin d
r ,
4
D
D
sin d I
3
D
E dunque
I3
1 q 0V z
2 4
1 q 0V z
2 4
sin d
D
0
1 q 0V z
1 q 0V z
sin
d
0
sin d 0
2 4 0
2 4
0
d
cos
d cos
0
d
cos
d cos 0
0
0
Resta così provata la tesi.
VERIFICA. Se la dimostrazione matematica di cui sopra non convincesse o se si volesse una
dimostrazione più veloce, anche se meno generale, si può calcolare il flusso attraverso una
superficie chiusa che sia simmettrica rispetto ad un asse, cioè una superficie di rotazione. Se l’asse
di simmetria è l’asse z allora si ha
B
0
dS
0
1 dr
1 dr
q V x
sin sin V y
sin cos dd
4 D r d
r d
76
0
4
1 dr
1 dr
q Vx
sin sin dd V y
sin cos dd
r d
D
D r d
0
4
2
2
1 dr
1 dr
qVx
sin d sin d V y
sin d cos d
r d
0
0
0
0 r d
Ma poiché risulta che
2
2
2
sin d d cos cos 0 0
0
0
2
2
cos d d sin sin
0
2
0
0
0
il flusso è proprio nullo.
DEDUZIONE,
CONSERVAZIONE DEL FLUSSO. Data una curva chiusa nello spazio, risulta che il flusso della
induzione magnetica attraverso una qualunque superficie che abbia come bordo tale curva è sempre
lo stesso.
DIMOSTRAZIONE. Consideriamo una linea chiusa γ.
Consideriamo poi due superfici 1 e 2 aventi come bordo
tale linea. Si ricorda che il verso di percorrenza del bordo di
una superficie determina anche il verso del campo normale
alla superficie stessa secondo la regola della mano destra. Si
ha dunque la situazione in figura.
Se ora diciamo ψ la superficie chiusa che si ottiene mettendo
assieme le superfici 1 e 2 , in base alla legge di Gauss per
la magnetostatica si ha
B 0 dS 0
D’altra parte è anche vero che
B 0 dS B 0 1 dS
1
B
B
B
0 2 dS
0 1 dS
0 2 dS
2
2
1
Dunque si è trovato che
B
1
0
1 dS B 0 2 dS
2
Ciò che prova la tesi.
77
DEFINIZIONE,
FLUSSO CONCATENATO. Definiamo flusso concatenato ad una curva chiusa γ orientata, il
flusso del campo di induzione che attraversi qualunque superficie avente per bordo la curva γ stessa.
La definizione è ben posta in quanto, in base al precedente teorema ad ogni curva chiusa orientata
corrisponde univocamente un flusso del campo di induzione.
DEDUZIONE,
TERZA EQUAZIONE DI MAXWELL. La divergenza della induzione magnetica nel vuoto è
data da
div B0 0
E’ l’analogo, nella magnetostatioca,
elettrostatica.
di quello che la prima equazione di Maxwell è nella
DIMOSTRAZIONE. In base alla legge di Gauss della magnetostatica si ha
B0 dS 0
Per il teorema della divergenza si ha
B0 dS div B0 dV
Da queste due relazioni si ottiene, per confronto, che
div B0 dV 0
Poiché questa relazione continua ad essere valida comunque si scelga un sottodominio di Ω, ne
segue che l’uguaglianza fra i due termini integrandi. E dunque la tesi.
VII) IL TEOREMA DI AMPERE
INTRODUZIONE. Il teorem da Ampère lega il campo di induzione magnetica alle correnti che lo
producono, ed è utile per il calcolo della induzione (in analogia a quanto già visto per la legge di
Gauss e il campo elettrico) quando le distribuzioni di corrente presentano opportune simmetrie.
DEDUZIONE,
L’INDUZIONE MAGNETICA NEL VUOTO NON E’ UN CAMPO CONSERVATIVO.
Consideriamo l’induzione magnetica determinata da una corrente stazionaria i che attraversi un
conduttore filiforme di percorso qualunque. Vogliamo provare che la circuitazione della induzione
magnetica lungo una qualunque curva chiusa concatenata con il conduttore stesso è non nulla,
ovvero che la induzione magnetica è non conservativa nello spazio.
DIMOSTRAZIONE. Proviamo quanto detto nel caso particolare in cui il conduttore sia rettilineo.
Sia γ una generica curva chiusa che concateni il conduttore. Il verso della curva lo si prenda
antiorario visto dalla corrente.
78
Se il sistema di riferimento ha asse z coincidente con il conduttore, con verso concorde a quello
della corrente, allora (legge di Biot e Savart) l’induzione magnetica si scrive
y
1
B0 x , y , z 0 i 2
x
2
2 x y
0
La curva d’altra parte avrà equazioni parametriche esprimibili come segue
x r sin cos
: y r sin sin
z r cos
0,2
La circutazione poi si scrive
B0 B0
0 y
x
i 2
dx 2
dy
2
2
2 x y
x y
0
y
x
i
x '
y ' d
2
2
2
2
2 0 x y
x y
2
Il calcolo delle derivate porge
x | r | sin cos r cos | cos r sin sin
y | r | sin sin r cos | sin r sin cos
Dunque si ha
y x | r sin sin r | sin cos r cos | cos sin sin
x y r sin cos r sin sin r cos sin sin cos
r r sin sin cos r sin cos cos sin sin cos
r r | sin 2 sin cos r 2 sin cos | sin cos sin 2 sin 2
|
|
|
2
|
2
|
2
2
Ne segue che
y x | x y |
r r | sin 2 sin cos r 2 sin cos | sin cos sin 2 sin 2
r r | sin 2 sin cos r 2 sin cos | cos sin sin 2 cos 2
r sin cos sin cos sin sin
2
|
sin sin
2
2
r sin cos cos sin sin cos
2
r2
2
|
2
2
2
sin 2 cos 2 r 2 sin 2
La circuitazione si scrive allora
79
0 2 y x ' x y '
0 2 y x ' x y '
d
i
d
B 0 B 0 2 i 0
2
2
2
2
2 0
x y
x y
0 2 r 2 sin 2
i
d
2 0 x 2 y 2
Osservato poi che
x 2 y 2 r 2 sin 2 cos 2 r 2 sin 2 sin 2 r 2 sin 2
si conclude che
B0 B0
0 2
i d 0 i
2 0
Ciò prova la non conservatività della induzione magnetica.
DEDUZIONE,
LEGGE DI AMPERE. La legge di Ampère è la generalizzazione della formula precedentemente
trovata per la circuitazione e si scrive
B
0
0 i
dove le correnti si considerano positive se ‘vedono’ antiotrario il verso della curva chiusa che le
concatena, negative altrimenti.
DEDUZIONE,
QUARTA EQUAZIONE DI MAXWELL NEI CASI STAZIONARI. Non è altro che la
espressione differenziale della legge di Ampère. Si scrive
rot B 0 0 j
DIMOSTRAZIONE. Si ricorre al teorema di Stokes applicato alla circuitazione della induzione
magnetica. Si ha
B 0 rot B 0 dS
S
S
Confrontando con la legge di Ampère si trova
rot B 0 dS 0 i
S
Tenendo poi conto che
80
i j dS
S
si scrive la forma integrale della quarta equazione di Maxwell
rot B 0 dS 0 j dS
S
S
che dovendo valere per ogni superficie S che sottenda la stessa curva chiusa implicherà la relazione
differenziale cercata
rot B0 0 j
La tesi è così dimostrata.
VII) IL TEOREMA DI EQUIVALENZA DI AMPERE
DEDUZIONE,
TEOREMA DI EQUIVALENZA DI AMPERE. Il teorema di equivalenza di Ampére consiste
nella constatazione che il dipolo elettrico e la spira piana percorsa da corrente (dipolo magnetico) si
comportano in modo formalmente uguale sia per quanto rigurda i campi da essi generati a grande
distanza (elettrico per il primo, di induzione magnetica per la seconda), sia per quanto riguarda la
sollecitazione agente su essi quando sono inseriti in un campo uniforme (elettrico per il primo, di
induzione magnetica per la seconda).
Per giustificare questo enunciato si riassumono qui i risultati delle analisi dei due dipoli fatte nei
relativi capitoli.
DIPOLO ELETTRICO
DIPOLO MAGNETICO
POTENZIALE SCALARE DETERMINATO A GRANDE DISTANZA
p r
V 0 P
4 0 r 3
1
m r
U 0 P 0 3
4 r
CAMPO DETERMINATO A GRANDE DISTANZA
3xz
p 3xz
B0 x P 0 m 5
E 0 x P
5
4
r
4 0 r
3 yz
p 3 yz
B0 y P 0 m 5
E 0 y P
4
r
4 0 r 5
2
3z r 2
B 0 z P 0 m
p 3z 2 r 2
E 0 z P
4
r5
4 0
r5
SOLLECITAZIONE AGENTE SUL DIPOLO IMMERSO IN UN CAMPO
UNIFORME
F 0
F 0
p E 0
m B 0
81
CAPITOLO V,
CAMPI ELETTRICI E MAGNETICI DIPENDENTI
DAL TEMPO
I) LA LEGGE DI FARADAY-NEUMANN-LENZ
RISULTATO SPERIMENTALE,
LEGGE DI FARADAY-NEUMANN-LENZ. Consideriamo una spira piana filiforme realizzata
da materiale conduttore. Fissiamo un verso positivo arbitrario su di essa. Prendiamo poi una
qualunque superficie S che abbia come bordo la spira stessa e fissiamo su di essa il campo del
versore normale in maniera tale che il versore stesso veda come antiorario il verso positivo fissato
sulla spira.
Allora la variazione del flusso del vettore induzione magnetica attraverso S è legata al sorgere di un
campo elettrico non conservativo all’interno del conduttore secondo la legge seguente
B
d
S
d
B
n dS
l Ei dt S dt
Questo campo elettrico è detto campo elettrico indotto ed è contrassegnato col pedice i. Ricordando
che la circuitazione del campo elettrico coulombiano è nulla, si può anche scrivere
B
d
S
d
B
E E E
S n dS
E
l l c i l i
dt
dt
dove
E c è il campo elettrico coulombiano;
E i è il campo elettrico indotto;
E E c Ei è il campo elettrico totale.
OSSERVAZIONE,
SIGNIFICATO DEL SEGNO MENO. Si osservi che il campo elettrico indotto è tale da produrre
una corrente elettrica la cui induzione magnetica produce un flusso che compensa la variazione di
flusso attraverso S.
OSSERVAZIONE,
GIUSTIFICAZIONE DELLA LEGGE DI FARADY-NEUMANN-LENZ. Se il flusso
attraverso la spira muta per movimento (o deformazione) della spira rispetto alla induzione
magnetica allora la legge di Farady-Neumann-Lenz può essere ricavata considerando l’effetto della
forza di Lorenz sulle cariche trasportate dal movimento della spira.
Il caso in cui invece l’induzione magnetica sia variabile e la spira sia invece fissa si può ricondurre
al primo se ci si mette in un sistema di riferimento in cui l’induzione magnetica risulti stazionaria e
la spira, viceversa, sia in moto.
82
DEDUZIONE,
SECONDA EQUAZIONE DI MAXWELL NEI CASI NON STAZIONARI. Il flusso attraverso
S può variare sia perché si sposta la spira, sia perché è il campo del vettore induzione magnetica a
variare.
Mettendoci nel caso generale in cui, rispetto al sistema di riferimento scelto, i punti della spira si
muovano con velocità
v v P
e il campo dell’induzione magnetica vari nel tempo, allora si trova che
B
P rot v P B P
rot E i P
t
DIMOSTRAZIONE. Consideriamo solo il caso in cui la spira sia fissa rispetto al sistema di
riferimento adottato. Allora la legge di Farady-Neumann-Lenz si scrive
B
B
d
S
n dS
E
l i
S t
dt
Applicando poi il teorema di Stokes a primo membro abbiamo
B
S rot Ei n dS S t n dS
Dovendo tale relazione valere per ogni superficie S avante bordo l possiamo scrivere
B
rot E i
t
Ora supponiamo che la spira si muova con velocità v v P , allora le cariche in essa presenti
avranno, punto per punto, tale velocità. Questo significa che saranno soggette alla forza di Lorentz a
cui si deve un campo
E i v P B P
che aggiunto a quello precedente mente trovato permette di scrivere
B
P rot v P B P
rot E i P
t
83
Questa rappresenta la seconda equazione di Maxwell per i casi non stazionari.
Si osserva che al posto del campo elettrico indotto si può anche mettere il campo elettrico totale,
cioè la somma del campo elettrico indotto e di quello coulombiano, visto che quest’ultimo ha rotore
nullo. Cioè la seconda equazione di Maxwell nei casi non stazionari si può scrivere anche
B
P rot v P B P
rot E P
t
essendo
rot E P rot E i P E c P rot E i P
OSSERVAZIONE SPERIMENTALE,
PRECISAZIONE SULLA SECONDA EQUAZIONE DI MAXWELL. Nella discussione
precedente la presenza di un conduttore filiforme è legata a necessità sperimentali. In realtà la
seconda equazione di Maxwell è indipendente dalla presenza di un circuito. Usando infatti, al posto
di un circuito, cariche di prova, si riscontra nello spazio un campo elettrico legato al campo di
induzione magnetica dalla espressione
B
rot Ei
t
E’ chiaro che in assenza di un circuito l’altra espressione della seconda equazione di Maxwell non
ha più significato.
II) AUTOINDUZIONE E CIRCUITO RL SERIE
DEDUZIONE,
FLUSSO
AUTOCONCATENATO
DEL
VETTORE INDUZIONE MAGNETICA. Sia
dato un generico circuito chiuso attraversato da
corrente. Il flusso della induzione magnetica, da
esso determinata e concatenato con il circuito
stesso, risulta proporzionale alla intensità di
corrente che lo attraversa, attraverso una costante
che dipende solo dai parametri geometrici della
spira.
DIMOSTRAZIONE. Dimostriamo la tesi nel caso particolare in cui il circuito chiuso sia piano e
circolare. Allora l’equazione della curva descritta dal circuito chiuso sia
x R cos
y R sin
0,2
In base alla prima legge di Laplace l’induzione magnetica determinata dal circuito nel generico
punto Q è data da
84
dl P PQ 0
t P PQ
B0 Q 0 i
i
dl
3
3
4 l
4 l
PQ
PQ
Considerato che
dx
d
t P
2
2
dx
dy
d
d
2
2
dx
dy
d
d
dy
d
dx
dy
dl
d
d
d
2
2
dove
dx
d R sin
dy R cos
d
si ha
R sin
t P dl
R cos
Inoltre noi consideriamo punti Q appartenenti al piano xy (il perché lo si vedrà in seguito). Il che
significa che
r cos R cos
PQ
dl P PQ
r sin R sin
i
R sin
r cos R cos
j
R cos
r sin R sin
k
0
0
0
0
R r sin sin r cos cos
Quindi l’induzione è
85
B0 Q
0 2
i
4 0
r
0
0
Rr sin sin cos cos
2
R 2 Rr cos cos sin sin
3
2
2
d
0
0
i
0
2
4
Rr sin sin cos cos
d
3
0 2
2
r R 2 Rr cos cos sin sin 2
Ora il flusso concatenato di questo campo può calcolarsi in particolare (per via della conservazione
del flusso concatenato della induzione magnetica) come il flusso attraverso il cerchio definito dalla
spira. Dunque tale flusso sarà
0 R 2 2
sin sin cos cos
B0 i
Rr
dddr
3
4 0 0 0 2
r R 2 2rRcos cos sin sin 2
Si osserva allora come il flusso concatenato con la spira sia proporzionale alla corrente che la
attraversa per mezzo della costante
0 R 2 2
Rr
4 0 0 0
sin sin cos cos
r
2
R 2rRcos cos sin sin
2
3
2
dddr
la quale dipende esclusivamente dalle caratteristiche geometriche della spira stessa. La tesi è
dunque dimostrata.
DEFINIZIONE,
COEFFICIENTE DI AUTOINDUZIONE. Consideriamo
un generico circuito attraversato da corrente. Dal precedente
teorema sappiamo che il flusso della induzione magnetica,
prodotta dal circuito, concatenato con il circuito stesso,
risulta proporzionale alla intensità di corrente che attraversa
il circuito. La costante di proporzionalità è detta coefficiente
di autoinduzione o induttanza e si indica L. Si pone dunque
B
L
i
In base a questa definizione la forza elettromotrice indotte dal circuito su sé stesso diviene
f .e.m. i L
d
i t
dt
86
L’induttanza si misura in weber su ampère, unità di misura a cui si dà il nome di henry (simbolo H).
DEFINIZIONE,
CIRCUITO RL SERIE. Definiamo circuito RL serie il circuito rappresentato in figura in cui si
realizza il collegamento in serie di un generatore di forza elettromotrice costante f.e.m., di un
resistore di resistenza R e di un avvolgimento di induttanza L.
DEDUZIONE,
CARICA DEL CONDENSATORE. Se l’interrottore viene chiuso all’istante t = 0, allora la
intensità di corrente che circola nel circuito varia nel tempo secondo la legge
R
t
f .e.m.
1 e L
i t
R
DIMOSTRAZIONE. Effettuando la circuitazione del campo elettrico lungo il circuito nel verso di
percorrenza della corrente si ha
f .e.m. u R t u L t 0
che si scrive più precisamente
f .e.m. i t R L
d
i t 0
dt
Abbiamo allora una equazione differenziale a variabili separabili che risolviamo nel modo seguente.
di t f .e.m. i t R
di t
dt
di
1
d
dt
L
f .e.m. i t R L
f .e.m. i R L 0
0
t
t
t
1 d f .e.m. i R 1
f .e.m. i t R
R
f .e.m. i t R
d ln
t
e L
R 0 f .e.m. i R
L0
f .e.m.
L
f .e.m.
t
t
R
Riordinando si ha infine
f .e.m. f .e.m.e
i t
R
t
R
L
R
t
f .e.m
1 e L
R
che è quanto volevasi dimostrare. L’andamento
della legge temporale trovata è indicato in figura.
DEDUZIONE,
ENERGIA FORNITA ALL’INDUTTANZA. L’energia accumulta dall’induttanza dopo il
superamento del transitorio è
U
1 f .e.m. 2 1
2
L
Li finale
2
2
2
R
87
DIMOSTRAZIONE. In base al principio di conservazione dell’energia si ha che l’energia
potenziale accumulata dall’induttanza deve essere pari all’energia erogata dal generatore5
f .e.m. i t dt f .e.m.
0
0
R
t
f .e.m.
f .e.m. 2
.1 e L dt
R
R
R
t
L
1
e
0
dt
f .e.m.
L
f .e.m. 2 Lf .e.m. 2
R
R
R
R2
2
meno l’energia dissipata in calore dalla resistenza R
2
R
f .e.m.
t
f .e.m. 2
L
0 Ri t dt R 0 R 1 e dt R
2
2
R
t
f .e.m. 2
L
0 1 e dt R
2R
R
t
t
L
0 1 e 2e L dt
2R
R
t
L
2R
L t L R f .e.m. 2
L
L
L
e
d t
2
2 e d t
2R 0
L
R0
L
R
2R
R
f .e.m. 2
2L L
f .e.m. 2 Lf .e.m. 2
R
2R
R
2R 2
f .e.m. 2
R
possiamo concludere che l’induttanza accumula l’energia
f .e.m. 2 Lf .e.m. 2 f .e.m. 2 Lf .e.m. 2 1 Lf .e.m. 2 1
2
Li finale
2
2
2
R
R
2
2
R
2R
R
La presenza dell’infinito nei calcoli precedenti si giustifica considerando che se il generatore
funziona a f.e.m. costante per un tempo infinito esso fornirà una quantità infinita di energia.
DEDUZIONE,
ENERGIA POTENZIALE DI UNA INDUTTANZA. Una induttanza, al pari di un condensatore,
accumula energia potenziale. In questo caso però tale energia è legata al campo di induzione
magnetica. In particolare l’energia accumulata da una induttanza L attraversata da una corrente i è
pari a
U
1 2
Li
2
DIMOSTRAZIONE. La dimostrazione di questa formula è implicita in quella della precedente
deduzione.
DEDUZIONE,
DENSITA’ DI ENERGIA DEL CAMPO DI INDUZIONE MAGNETICA. Ad un campo di
induzione magnetica è associata una quantità di energia potenziale per unità di volume pari a
5
In questi calcoli si considera il seguente risultato dell’analisi sugli integrali impropri
e
x
dx 1
0
88
1 B 0 P
u 0 P
2 0
2
dove i pedici zero stanno ad indicare che questa formula si riferisce al caso in cui l’induzione
magnetica abbia sede nel vuoto. In un altro capitolo questa espressione verrà opportunamente
generalizzata.
DIMOSTRAZIONE. Dimostriamo questa formula del tutto generale in un caso particolare molto
semplice. Consideriamo cioè nuovamente il circuito RL serie e supponiamo che l’induttanza in
esso presente sia quella di un solenoide toroidale. Sappiamo che l’energia potenziale immagazzinata
dal campo di induzione del solenoide è
U
1 2
Li
2
D’altra parte un solenoide toroidale ha la proprietà di racchiudere dentro di sé tutta l’induzione
magnetica da esso generata. Quindi la densità di energia potenziale del suo campo di induzione
magnetica si ottiene dividendo l’energia potenziale totale per il volume del solenoide.
Se il raggio della sezione circolare del solenoide vale r e quello dell’asse circolare del solenoide
vale R, allora, per il primo teorema di Guldino, il volume del solenoide toroidale vale
V r 2 2R 2 2 r 2 R
Ma quanto vale l’induttanza di un solenoide toroidale? Ricordando che
B
L
i
allora si ha approssimativamente
Nr 2 B0
i
dove si è assunta costante l’induzione dentro il solenoide e dove N è il numero di spire del
solenoide. Quindi l’energia potenziale immagazzinata dalla induzione prodotta dal solenoide
toroidale vale
B0 Nr 2 B0 L
U
1 2 1
Li Nr 2 B0 i
2
2
Ma allora l’energia immagazzinata per unità di volume dalla induzione prodotta dal solenoide
toroidale vale
u0
U 1
1
1 NB0 i
Nr 2 B0 i 2 2
V 2
2 r R 4 R
Tenendo presente l’espressione della induzione del solenoide B0
0 Ni
2 r2 2R2
0 Ni
si ha
2R
89
1 NB0 i 1 Ni 0 Ni
1 0 Ni 0 Ni B0
u0
4 R
4 R 2R 2 0 2R 2R 2 0
2
Questa formula trovata in un caso così particolare può essere applicata ad ogni campo di induzione
magnetica. La tesi è dimostrata.
III) MUTUA INDUZIONE E CIRCUITI ACCOPPIATI
DEDUZIONE,
FLUSSO
CONCATENATO
DEL
VETTORE INDUZIONE MAGNETICA.
Siano dati due circuiti attraversati da
corrente. Allora il flusso della induzione
determinata dal primo circuito, concatenato
con il secondo circuito,
risulta
proporzionale alla intensità di corrente che
attraversa il primo circuito, attraverso una
costante che dipende solo dalla forma dei
due circuiti e dalla loro posizione relativa.
DIMOSTRAZIONE. Dimostriamo la tesi nel caso in cui il secondo circuito sia una spira piana. Si
abbiano allora il circuito descritto dalla curva chiusa generica 1 attraversato dalla corrente i1 , ed il
circuito descritto dalla circonferenza 2 attraversato dalla corrente i 2 . Vogliamo calcolare il flusso
della induzione magnetica determinata dal primo circuito attraverso il secondo circuito.
Calcoliamo allora anzitutto l’induzione magnetica determinata dal primo circuito nello spazio. La
prima formula di Laplace porge
i
dl r i dx1
dB0 1 P 0 i1 3 0 13
4
4 r d 1
r
x
j
dy1
d 1
y
k
dz1
d 1
z
dy1
dz
z 1
d 1
d 1
i dz
dx
d 1 0 13 1 x 1
4 r d 1
d 1
dx1 y dy1
d
d 1
1
y
z d 1
x
Considerando tuttavia punti P del piano xy (il perché lo si capirà in seguito) abbiamo
i
j
dy1
d 1
y
k
dz1
d 1
0
i dx1
dB01 P 0 13
4 r d 1
x
dz1
y
d 1
i
dz1
d 1 0 13
x
4 r
d 1
dx1 y dy1
d
d 1
1
d 1
x
dove
90
dx1
|
|
d r 1 sin 1 cos 1 r 1 cos 1 1 cos 1 sin 1 sin 1
1
dy1
r | 1 sin 1 sin 1 r 1 cos 1 | 1 sin 1 sin 1 cos 1
d 1
dz1
r | cos r sin |
d 1
r 3 x1 x y 1 y z1 z
2
2
3
2 2
r 1 sin 1 cos 1 x r 1 sin 1 sin 1 y r 1 cos 1 z
2
2
3
2 2
Dunque l’induzione prodotta dal primo circuito in un qualunque punto P del piano xy è
dz1
y
d 1
0 2 1
dz1
B01 P
i1 3
x
4 0 r
d 1
dx1 y dy1
d
d 1
1
2
1 dz
y 3 1 d 1
d
r
1
0
2
0 i1
1 dz1
d
x
d
1
0 r 3 d 1 1
3
4
r
2
2
1 dx1
1 dy1
x
d 1 x 3
d 1
y 3
d 1
0 r
0 r d 1
Il flusso della induzione magnetica del primo circuito, concatenato con il secondo circuito può
essere calcolato, per via della conservazione del flusso di un campo solenoidale, attraverso una
qualsiasi superficie avente bordo 2 . Scegliendo allora il cerchio di bordo 2 si ha
cos 2 0
2 B 01 B 01 P P dS B 01 sin 2 0 dd 2
S
0 0
1
0
2 R
dz1
sin 2
d 1
0
2 R
0 2 1
dz1
i1 3
cos 2
d 1 0 dd 2
4 0 r
d 1
0 0
1
dx1 sin dy1 cos
2
2
d
d 1
1
0 2 R 2 1 dx1
dy
i1 3
sin 2 1 cos 2 d1dd 2
4 0 0 0 r d1
d1
dove
91
dx1
|
|
d r 1 sin 1 cos 1 r 1 cos 1 1 cos 1 sin 1 sin 1
1
dy1 r | sin sin r cos | sin sin cos
1
1
1
1
1
1
1
1
1
d 1
r x1 x y 1 y z 1 z
3
2
2
3
2 2
r 1 sin 1 cos 1 cos 2 r 1 sin 1 sin 1 sin 2 r 1 cos 1
2
2
2
2
3
2
Si vede effettivamente come il flusso
concatenato con il secondo circuito
della induzione prodotta dal primo
circuito sia proporzionale alla corrente
che attraversa il primo circuito
attraverso una costante legata alla
forma del primo circuito e del secondo
e alla loro disposizione relativa.
La tesi è dunque dimostrata.
DEFINIZIONE,
COEFFICIENTE DI MUTUA INDUZIONE. Consideriamo, come sopra, due circuiti. Allora il
flusso della induzione magnetica del primo circuito, concatenato con il secondo circuito, risulta
proporzionale, per il precedente teorema, alla corrente che transita nel primo circuito. La costante di
proporzionalità e detta coefficiente di muta induzione del primo circuito sul secondo e si pone
B
01
2
M 12
i1
Analogamente si definisce coefficiente di mutua induzione del secondo circuito sul primo la
costante definita come segue
B
1 02
M 21
i2
In base a queste posizioni e alla legge di Farady-Neumann-Lenz, la forza elettromotrice indotta
dalla corrente del primo circuito sul secondo circuito può esprimersi
f .e.m. i 2 M 12
d
i1 t
dt
mentre la forza elettromotrice indotta dal secondo circuito nel primo può scriversi
f .e.m. i1 M 21
d
i2 t
dt
92
DEDUZIONE,
UGUAGLIANZA FRA I DUE COEFFICIENTI DI MUTUA INDUZIONE. Consideriamo al
solito i due circuiti nello spazio. Allora il coefficiente di mutua induzione del secondo circuito sul
primo è uguale al coefficiente di mutua induzione del secondo sul primo circuito.
DIMOSTRAZIONE. Per dimostrare questa importante proprietà ci riferiamo ad un caso
particolare e seplice da trattare. Si considerino infatti i due circuiti indicati in figura.
Le due curve che descrivono i due circuiti sono le seguenti.
x1 R cos 1
y1 R sin 1
1
1 0,2
x 2 R cos 2
y 2 D R sin 2
2
2 0,2
Calcoliamo anzitutto l’induzione del primo circuito nei punti del piano xy (ci interessa l’induzione
in questi punti poiché siamo interessati al flusso di tale induzione attraverso il cerchio individuato
dal secondo circuito). La prima formula di Laplace porge
dB01 P
i
j
k
0 dl r 0 i1
i1 3
R sin 1
R cos1
0 d1
4
r
4 r 3
x R cos1 y R sin 1 0
d1
2
2
2
2
yR sin 1 R sin 1 xR cos1 R cos 1
0
0
i1
0
d 1
3
4
2
2 2
2
x R cos1 y R sin 1 yR sin 1 R xR cos1
0
0
i
0 13
4 r
Integrando si ha
B 0 1 P
0 i1
4
2
0
0
0
Ry sin R 2 Rx cos
1
1
d 1
3
2
2 2
x R cos 1 y R sin 1
0
0 Ri 1
0
4 2
y
sin
R
x cos 1
1
0
2
2
x R cos 1 y R sin 1
3
2
d 1
93
Considerando ora che i punti del cerchio delimitato dal secondo circuito sono dati da
x cos 2
P
y D sin 2
2 0,2
0, R
il flusso di tale induzione concatenato con il secondo circuito è
0
0
0 Ri 1 2 R
2 B0 1
0
0 dd 2
4 0 0 2
D
sin
sin
R
cos
cos
2
1
2
1
d 1 1
3
0
2
2 2
cos 2 R cos 1 D sin 2 R sin 1
Ri 2 R 2
D sin 2 sin 1 R cos 2 cos 1
0 1
d 1 dd 2
3
4 0 0 0
2
2 2
cos 2 R cos 1 D sin 2 R sin 1
Ne segue che
M 12
0 R 2 R 2
4 0 0 0
D sin 2 sin 1 R cos 2 cos 1
cos
R cos 1
2
2
3
2 2
D sin 2 R sin 1
d 1 dd 2
Calcoliamo ora l’induzione del secondo circuito nei punti del piano xy. La prima formula di
Laplace porge
dB0 2 P
0
4
0
4
i
j
k
0 dl r 0 i 2
i2
R sin 2
R cos 2
0 d
4
4 r 3
r3
x R cos 2 y D R sin 2 0
x R cos
x R cos
i2
2
2 2
2 y R sin 2 D
3
i2
2
2 2
2 y R sin 2 D
3
0
0
d
y D R sin R 2 xR cos
2
2
0
0
d 2
D y R sin R 2 xR cos
2
2
Integrando si ha
i
B 0 2 P 0 2
4
2
0
0
0
D y R sin R 2 xR cos
2
2
d 1
3
2
2 2
x R cos 2 y R sin 2 D
94
0
0 Ri 2
0
4 2
D
y
sin
R x cos 2
2
0
2
2
x R cos 2 y R sin 2 D
3
2
d 2
Considerando ora che i punti del cerchio delimitato dal primo circuito sono dati da
x cos1
P
y sin 1
1 0,2
0, R
il flusso di tale induzione concatenato con il secondo circuito è
1 B0 2
0
0
0 Ri 2 2 R 0 Ri 2
0
0 dd 1
4 0 0 4 2
D sin 1 sin 2 R cos 1 cos 2
d 2 1
3
0
2
2 2
cos 1 R cos 2 sin 1 R sin 2 D
2 R 2
D sin 1 sin 2 R cos 1 cos 2
Ri
0 2
d 1 dd 2
3
4 0 0 0
2
2 2
cos 1 R cos 2 sin 1 R sin 2 D
Dunque si è ottenuto
Ri
M 21 0 2
4
2 R 2
0 0 0
D sin 1 sin 2 R cos 1 cos 2
cos R cos
1
2
2
3
2 2
sin 1 R sin 2 D
d 1 dd 2
il quale non è apparentemente uguale all’altro coefficiente di mutua induzione. Tuttavia posto
1
2
si ha
0 R 2 R 2
M 21
4 0 0 0
0 R 0 R 0
4 2 0 2
D sin sin R cos cos
cos R cos
2
sin R sin D
D sin sin R cos cos
cos R cos
2
3
2 2
3
2 2
D sin R sin
ddd
ddd
95
Operando ora le sostituzioni
2 2 0
2 2
0 2 2
2 1 0
0 1 2
1 2
si ha
M 21
0 R 2 R 2
4 0 0 0
D sin 2 sin 1 R cos 2 cos 1
cos
R cos 1
2
2
3
2 2
D sin 2 R sin 1
d 2 dd 1
e dunque
M 21 M 12
il che dimostra la tesi.
DEDUZIONE,
CIRCUITI ACCOPPIATI. Dati due circuiti nello spazio, C1 e C2 , percorsi dalle correnti i1 e i 2
rispettivamente, detto M il coefficiente di mutua induzione fra di essi, allora valgono
simultaneamente le relazioni
di1
di 2
f .e.m.1 L1 dt M dt R1i1
f .e.m. L di 2 M di1 R i
2
2
2 2
dt
dt
con il seguente significato dei simboli
f .e.m.1 forza elettromotrice del primo circuito
f .e.m. 2 forza elettromotrice del secondo circuito
L1 coefficiente di autoinduzione del primo circuito
L2 coefficiente di autoinduzione del secondo circuito
M = coefficiente di mutua induzione fra i due circuiti
R1 resistenza del primo circuito
R2 resistenza del secondo circuito
DEDUZIONE,
ENERGIA POTENZIALE MAGNETICA DEI CIRCUITI ACCOPPIATI. Dati i due circuiti
accoppiati sopra introdotti ad essi compete l’energia potenziale magnetica
U
1
1 I1 2 I 2
2
96
dove si intende che il primo flusso è il flusso concatenato complessivo col primo circuito (cioè
autoconcatenato e non). Stesso discorso per il secondo flusso.
DIMOSTRAZIONE. Il lavoro fatto dal primo generatore è
W1 f .e.m.1 i1 dt R1 i1 dt L1 i1
2
0
0
R1 i1 dt
2
0
0
1
2
di1
di
2
dt M i1 2 dt R1 i1 dt L1 i1 di1 M i1 di 2
dt
dt
0
0
0
0
I
I
I2
1
2
L1 I 1 M i1 di 2
2
0
dove si è assunto che la corrente nei due circuiti sia inizialmente nulla e dove si sono introdotte le
due correnti a regime.
Analogamente il lavoro fatto dal secondo generatore vale
W2
0
I
I
1
2
di
di
2
f .e.m.2 i2 dt R2 i2 dt L2 i2 2 dt M i2 1 dt R2 i2 dt L2 i2 di2 M i2 di1
dt
dt
0
0
0
0
0
0
R2 i2 dt
2
0
2
I
1
1
2
L2 I 2 M i2 di1
2
0
Il lavoro complessivamente fatto dai due generatori è pertanto
I1
I2
2
1
1
2
2
2
W1 W2 R1 i1 dt R2 i2 dt L1 I 1 L2 I 2 M i1di2 i2 di1
2
0
0
0
0
2
ed osservato che
I1
I2
di2
di2
di1
di
M i1di2 i2 di1 M i1
dt i2
dt M i1
i2 1 dt
dt
dt
0
0
0 dt
0 dt
0
I1I 2
d i1i2
M
dt M d i1i2 MI 1 I 2
0
0 dt
tale lavoro si scrive
2
1
1
2
2
2
W1 W2 R1 i1 dt R2 i2 dt L1 I 1 L2 I 2 MI 1 I 2
2
0
0
2
Di questo lavoro tuttavia una parte si trasforma in calore, dissipato per effetto Joule dalle due
resistenze. Dunque l’energia potenziale magnetica che compete realmente ai circuiti accoppiati è
U
1
1
2
2
L1 I 1 L2 I 2 MI 1 I 2
2
2
Osserviamo ora che il flusso complessivamente concatenato col primo circuito è
97
1 I1 L1 I 2 M
mentre quello concatenato con il secondo vale
2 I 2 L2 I1M
dunque si ha
1
1 I1 2 I 2 1 L1 I12 L2 I 2 2 2 MI 1 I 2 1 L1 I12 1 L2 I 2 2 MI 1 I 2 U
2
2
2
2
e la tesi è dimostrata.
IV) CORRENTE DI SPOSTAMENTO E QUARTA EQUAZIONE DI
MAXWELL
OSSERVAZIONE SPERIMENTALE,
QUARTA EQUAZIONE DI MAXWELL IN CASI NON STAZIONARI Sperimentalmente si
trova che in punti sede di campi elettrici variabili si originano campi magnetici secondo la legge
DP, t
rot H P, t J P, t
t
la quale rappresenta l’estensione della quarta equazione di Maxwell ai casi non stazionari.
OSSERVAZIONE,
SULLA QUARTA EQUAZIONE DI MAXWELL. CORRENTE DI SPOSTAMENTO. La
quarta equazione di Maxwell nella sua espressione generale ci dice che non solo le cariche in moto
determinano campi magnetici, ma anche campi elettrici variabili determinano campi magnetici.
Tuttavia in genere si introduce il campo vettoriale
D P, t
J S P, t
t
detto densità di corrente di spostamento, in modo da ricondurre, formalmente, la quarta equazione
di Maxwell alla espressione dei casi stazionari
rot H P, t J T P, t
dove però, questa volta, a secondo membro si ha una densità di corrente detta totale, data da
J T P , t J P , t J S P , t
La particolarità di questa densità di corrente è di essere sempre un campo solenoidale, là dove la
densità di corrente J P, t lo è solo in caso stazionario. Infatti si ha
98
D
lib P, t
P, t
div J T P, t div J P, t div J S P, t
div
t
t
dove si è sfruttata la legge di conservazione della carica e la definizione di densità di corrente di
spostamento. Ora se si tiene presente la prima legge di Maxwell si ha
div D
P, t
D
P, t
div
div J T P, t div J P, t div J S P, t
t
t
che, in base al teorema di Schwartz, porge appunto
D
D
P, t 0
P
,
t
div
div J T P, t div
t
t
La densità di corrente totale presenta tre componenti. Una componente è la densità di corrente
dovuta al moto delle cariche libere, un’altra è la densità di corrente dovuta al moto di cariche
prodotte dalla polarizzazione del dielettrico, ed un’altra è invece una densità di corrente presente
anche nel vuoto, che dunque non ha nulla a che vedere con il motot di cariche. Tale densità di
corrente, che diciamo fantasma, è data da
E P , t
0
t
Dimostriamo tutto ciò. Partiamo dalla espressione della densità di corrente totale che possiamo
riscrivere come
E
P, t
P
,
t
P
0
P , t
E
P
,
t
P
J P , t
J T P , t J P , t
0
t
t
t
Si osservi ora che la legge di conservazione della carica per cariche di polarizzazione si scrive
div P
P, t
pol P, t
P P , t
div J pol P, t
div
t
t
t
dove si è ricorso al legame trovato nel capitolo due tra l’intensità di polarizzazione e la carica di
polarizzazione. Dunque possiamo dedurre la densità di corrente dovuta al moto delle cariche di
polarizzazione si esprime
PP, t
J pol P, t
t
Tornando alla densità di corrente totale si ha quindi
99
E
P, t
P
,
t
P
0
E P , t
J T P , t J P , t
J P , t 0
J pol P, t
t
t
che è quanto volevasi dimostrare. Si aggiunge solo che in base a quanto visto la corrente di
spostamento si scrive come somma di due componenti. Infatti
E P, t
J S P, t 0
J pol P, t
t
100
CAPITOLO VI,
FENOMENI
MAGNETICI
PRESENZA DI MATERIA
STAZIONARI
IN
I) SORGENTI DI INDUZIONE MAGNETICA NELLA MATERIA
INTRODUZIONE. Nel capitolo IV sono state discusse le proprietà del campo magnetico
stazionario nel vuoto. Qui invece verranno discussi i cambiamenti che è necessario apportare allo
studio dei fenomeni magnetici stazionari quando nello spazio è presente la materia.
Il fatto che esistano materiali in grado di generare campi di induzione magnetica, senza che vi sia
moto di cariche, induce ad ammettere che l’induzione magnetica abbia due sorgenti, di cui una è la
corrente elettrica, come già visto, ed una è invece interna al materiale.
Nel seguito proponiamo un modello della materia che ci permetta di esprimere in termini
matematici questa sorgente di induzione magnetica interna alla materia stessa.
OSSERVAZIONE SPERIMENTALE,
STRUTTURA DEI MEZZI MATERIALI. Consideriamo il seguente modello di mezzo. Materia
formata da particelle a ciascuna delle quali si attribuisce un momento magnetico m dovuto al moto
delle cariche che costituiscono gli atomi.
DEFINIZIONE,
VETTORE INTENSITA’ DI MAGNETIZZAZIONE.
magnetizzazione di un mezzo il vettore
Definisco
vettore
intensità
di
N m
M
V
dove N è il numero di particelle nel volume V e m è il valore medio del momento di dipolo
magnetico delle particelle del dielettrico all’interno di tale volume.
Il volume V deve essere sufficentemente piccolo da fornire per M valori che variano con
continuità e abbastanza grande da consentire una media affidabile per m .
DEDUZIONE,
CORRENTI
ATOMICHE.
Diciamo
correnti
atomiche di un mezzo quelle dovute al moto delle
cariche dei suoi atomi. Se indichiamo J at il campo
della densità di corrente associato a tali correnti, allora
si può dimostrare che sussiste la relazione
J at rot M
DIMOSTRAZIONE. Consideriamo un dielettrico di
volume V. Un suo volume dV si può considerare un
101
dipolo magnetico di momento N m M dV . Il potenziale vettore, in P, determinato dal
volumetto dV risulta dato da
M O OP
d A0 P 0
dV
3
4
OP
Se ora consideriamo un sistema di riferimento centrato non più in O ma in P sarà conveniente
scrivere
M O PO
d A0 P 0
dV
3
4
PO
Si osservi ora che
PO
1
3
PO
PO
dunque si potrà scrivere
d A 0 P
0
4
1
M
O
dV
PO
Ora ricordando la regola di calcolo vettoriale secondo cui
F g rot F g rot F g
si ha
rot M O
M
0
O
rot
dV
d A 0 P
4
PO
PO
D’altra parte il potenziale vettore del volume elementare di dielettrico è anche dato, per quanto visto
nello studio della funzione potenziale vettore, da
J O
d A 0 P 0 at
dV
4 PO
Dunque risulta
102
rot M O
M
J O
M
O
O
rot
at
J
O
rot
M
O
PO
rot
at
PO
PO
PO
PO
Adesso supponiamo che le correnti atomiche siano stazionarie. Allora la conservazione della carica
impone che sia
div J at O 0
Imponendo che il secondo membro della uguaglianza ottenuta più sopra soddisfi a questa relazione
si ha
M
O
div rot M O div POrot
0
PO
Ricordando ora che la divergenza del rotore vale zero si ottiene
M
M
M
O
M
O
O
0 POdiv rot
PO rot
PO rot O 0
div POrot
PO
PO
PO
PO
Ma essendo
PO
PO
PO
0,
O P
deve risultare necessariamente
M
O 0
rot
PO
Dunque si è trovato che
M
O
O
J at O rot M O POrot
rot
M
PO
cioè la tesi.
OSSERVAZIONE,
TERZA EQUAZIONE DI MAXWELL IN PRESENZA DI MEZZI MATERIALI. La terza
equazione di Maxwell resta inalterata anche in presenza di mezzi materiali poiché la natura delle
103
correnti che originano l’induzione magnetica non influisce sulle caratteristiche della stessa. Resta
ancora valida dunque la relazione
div B 0
DEDUZIONE,
QUARTA EQUAZIONE DI MAXWELL IN PRESENZA DI MEZZI MATERIALI. La quarta
equazione di Maxwell all’interno di un mezzo materiale diviene
rot B 0 J J at 0 J rot M
che possiamo anche scrivere
B
M
0
rot
J
0
dove il vettore J indica la densità di corrente dovuta a circuiti macroscopici, quella che è cioè
direttamente misurabile.
DEFINIZIONE,
IL VETTORE INTENSITA’ DI CAMPO MAGNETICO. In genere si usa ragionare, anziché
con il vettore M , con un altro vettore, detto intensità del campo magnetico, definito dalla relazione
seguente
H
B
0
M
Si osserva che questo vettore risulta determinato dalle correnti esterne, cioè da quelle correnti
direttamente misurabili. Infatti si ha evidentemente
rot H J
Si trova che il vettore intensità di campo magnetico si misura in ampere su metro.
II) RELAZIONI FRA B, H ED M
INTRODUZIONE. Stabiliamo ora delle relazioni fra i tre vettori magnetici introdotti.
DEFINIZIONE,
SUSCETTIVITA’ MAGNETICA. Nel caso di dielettrici isotropi il vettore M
proporzionale al campo magnetico. In questi casi si pone
risulta
104
M
H
Si noti la deffernza di questa posizione con l’analoga della elettrostatica, ovvero con la
P
0 E
0
I due simboli usati sono uguali, ma nei due contesti hanno significato diverso. La della
magnetostatica prende il nome di suscettività magnetica del mezzo. Essa è una grandezza
adimensionata. Nel caso di materiali diamagnetici e paramagnetici (la maggiopranza dei materiali)
la suscettività è una costante. Per altri materiali (ferro e materiali ferromagnetici) risulta che è
una funzione di H. Inoltre si ha che
1) 0 per i materiali paramagnetici (aria, alluminio, platino etc);
2) 0 per i materiali diamagnetici (rame, argento, acqua etc).
DEFINIZIONE,
PERMEABILITA’ MAGNETICA RELATIVA E ASSOLUTA. Nel caso di isotropia del mezzo
si ha
B
M H H
H H 1
H
0
0
0 1
B
B
La grandezza 1 prende il nome di permeabilità magnetica relativa del mezzo e si pone
r 1
Dunque la relazione fra intensità di campo magnetico e induzione magnetica in mezzi isotropi
diviene
H r 0 B
Se definiamo poi la permeabilità magnetica assoluta come
r 0
tale relazione si scrive
HB
TABELLA,
TERZA E QUARTA EQUAZIONE DI MAXWELL NEI DIELETTRICI.
105
TERZA EQUAZIONE
DI MAXWELL
CASO GENERALE
div B 0
ISOTROPIA
div B 0
ISOTROPIA E
OMOGENEITA’
QUARTA EQUAZIONE DI MAXWELL
B
0 M
rot
J
rot
H
J
0
B
rot
0 r
div B 0
rot B
0 r
J rot B j rot H
J
J
rot B
j rot H J
DEDUZIONE,
SUPERFICIE DI SEPARAZIONE E INDUZIONE MAGNETICA. Consideriamo la superficie
di separazione fra due mezzi accostati. Nel passaggio dall’uno all’altro l’induzione magnetica
conserva la sua componente normale alla superficie. Dunque
Bn1 Bn 2
DIMOSTRAZIONE. Sfruttando la terza equazione di Maxwell si dimostra questa proprietà in
modo analogo a quello adottato per la dimostrazione della conservazione della componente normale
dello spostamento elettrico alla superficie di separazione fra due dielettrici.
DEDUZIONE,
SUPERFICIE DI SEPARAZIONE E CAMPO MAGNETICO. Consideriamo la superficie di
separazione fra due mezzi accostati. Nel passaggio dall’uno all’altro il campo magnetico conserva
la sua componente tangente alla superficie. Dunque
H t1 H t 2
DIMOSTRAZIONE. Questa proprietà si dimostra sfruttando la quarta equazione di Maxwell che
si scrive, in questo caso
rot H 0
Si procede come nella dimostrazione della componente tangente del campo elettrico al passaggio da
un dielettrico ed un altro ad esso accostato.
DEDUZIONE,
RIFRAZIONE DELLE LINEE DI FORZA. Ricaviamo ora un legame fra l’angolo che
lìinduzione magnetica forma con la normale alla superficie di separazione e le permeabilità relative
dei mezzi.
In base a considerazione geometriche (vedi figura) abbiamo
106
Bt1
tan 1 B
tan 1 Bt1
n1
tan 2 Bt 2
tan Bt 2
2
Bn 2
Poiché poi
B1 H 1 r 0 Bt1 H t1 r1 0
B 2 H 2 r 0 Bt 2 H t 2 r 2 0
allora
tan 1 H t1 r1 0
tan 2 H t 2 r 2 0
Ma essendo H t1 H t 2 segue che
tan 1 r1 0
tan 2 r 2 0
III) MATERIALI
MEZZI AMAGNETICI. Sono materiali la cui permeabilità magnetica relativa è indipendente dal
campo magnetico applicato e risulta r 1 . Essi si dividono in
1) MEZZI DIAMAGNETICI, nei quali r 1i.e. 0 ;
2) MEZZI PARAMAGNETICI, nei quali r 1i.e. 0 .
DEDUZIONE,
MEZZI AMAGNETICI E INDUZIONE MAGNETICA. La presenza di un mezzo diamagnetico
smorza l’induzione magnetica, la presenza di un mezzo paramagnetico la amplifica.
DIMOSTRAZIONE. Consideriamo l’espressione della intensità di magnetizzazione nel caso di
mezzo isotropo. Si ha
M H
Ma la suscettività magnetica è data da
r 1
dunque l’intensità di magnetizzazione si scrive
M r 1 H
107
D’altra parte il campo magnetico per mezzi isotropi si scrive
B
H
r 0
e dunque l’intensità di magnetizzazione si scrive
M
r 1 B
r 0
Questo vuol dire che nel caso di mezzi diamagnetici i momenti magnetici atomici sono mediamente
opposti alla induzione magnetica, che dunque ne risulta smorzata; nel caso di mezzi paramagnetci i
momenti magnetici atomici sono mediamente concordi alla induzione magnetica, che dunque ne
risulta amplificata.
OSSERVAZIONE,
VALORE DELLA PERMEABILITA’ MAGNETICA RELATIVA DEI MEZZI
AMAGNETICI. Si vuole far presente che i mezzi amagnetici hanno permeabilità magnetica
relativa molto prossima ad uno, dunque il loro effetto sulle formule della magnetostatica ricavate
nel vuoto è minimo. Basti osservare i valori riportatai nella tabella seguente.
MEZZI DIAMAGNETICI
Azoto (1 Atm)
Idrogeno (1 Atm)
Acqua pura
Mercurio
r 1
1 5 10 9
1 2,1 10 9
1 9 10 6
1 3,2 10 5
Rame
1 8,9 10 6
MEZZI PARAMAGNETICI
r 1
Aria (1 Atm)
Ossigeno (1 Atm)
Alluminio
Platino
1 4 10 7
1 2,1 10 6
1 2,3 10 5
1 3 10 4
OSSERVAZIONE SPERIMENTALE,
LEGGE DI CURIE. La permeabilità magnetica relativa dei materiali diamagmetici risulta
indipendente dalla temperatura. Invece la permeabilità magnetica dei mezzi paramagnetici risulta
legata alla temperatura dalla legge
C
T
dove
108
C è una costante del particolare materiale;
T è la temperatura;
r 1 è la suscettività magnetica del materiale.
MEZZI FERROMAGNETICI. Dal punto di vista
microscopico i materiali ferromagnetici sono formati da
sub unità caratterizzate dal fatto che le molecole (o gli
atomi) che le costituiscono presentano tutte momento
magnetico con stesso verso e direzione. Queste sub unità
sono dette domini di Weiss e hanno le dimensioni di
10 3 10 6 m.
Se il materiale è allo stato nativo i momenti magnetici dei
domini di Weiss sono orientati casualmente, producendo
quindi una magnetizzazione macroscopicamente nulla.
In presenza di un campo magnetico esterno, tuttavia, i
momenti magnetici tendono ad allinearsi. Tale
allineamento permane anche se il campo magnetico esterno
è rimosso, dando origine ad una magnetizzazione residua.
A partire da un valore critico TC della temperatura
(temperatura di Curie, vedi tabella successiva) si ha un comportamento paramagnetico ed è dunque
definibile una suscettività magnetica χ la quale segue la legge di Curie-Weiss
C
T TC
Questi materiali, che per giunta hanno anche un buon comportamento meccanico, sono di
fondamentale importanza per le applicazioni industriali poiché sono sede
di intense
magnetizzazioni anche in presenza di deboli campi di eccitazione.
L’effetto magnetizzante è il risultato dell’equilibrio statistico tra l’azione ordinatrice del campo e
quella dell’agitazione termica che porta alla completa smagnetizzazione quando si raggiunge la
temperatura di Curie del materiale.
m
rMAX
B g T
Br T
2 10 5
175
2,16
1,2
1,79
0,31
4
1000
7 10 3
2,14
0,8
40
Nichel
1,1 103
0,61
0,33
130
NichelFerro 50%
7 10 4
1,55
0,73
40
Ferro puro
Cobalto
FerroSilicio 4%
5 10 4
1,08
0,6
MAGNETI PERMANENTI
Hc A
Tc C
770
1131
360
4
Acciaio al
1,05
5600
Tungsteno
Anico (lega
Fe-Al-Ni1,25
50000
Co)
CURVA DI MAGNETIZZAZIONE. I materiali ferromagnetici sono caratterizzati mediante le
curve di magnetizzazione, cioè mediante diagrammi che forniscono il valore in modulo e in verso
109
dell’induzione magnetica B in funzione del campo magnetico H per apparati sperimentali del tipo di
quelli di seguito illustrati.
Un toro di materiale ferromagnetico è fittamente avvolto da una spira in cui transita una corrente I.
Ricordando che, per definizione di campo magnetico, risulta
rot H J
se allora R è il raggio medio del toro si potrà scrivere, per il
teorema di Stokes, che
rot H dS J dS H dl J dS H 2R NI
S
S
S
S
dove si è indicato S il cerchio di raggio R. Dunque si ha
H
NI
2R
Si consideri ora che intorno al toro vi sia un secondo avvolgimento, diciamo di n spire. Questo
avvolgimento sia collegato ad un voltmetro. Al variare della corrente I il flusso concatenato con il
secondo avvolgimento varia e si produce una forza elettromotrice indotta
d S B
d
B
A n dA A dB
f .e.m. i
dt
dt
dt
letta dal voltmetro. Dalla sua conoscenza si ricava il valore della induzione magnetica nel materiale
ferromagnetico.
Il diagramma di magnetizzazione
si costruisce con i seguenti
passaggi.
1)Se il ferro che costituisce il
toro
all’inizio
non
è
magnetizzato, aumentando la
corrente
che
circola
nell’avvolgimento primario, e
cioè H, si trova che aumenta
anche B, seguendo la curva OA
(detta di prima magnetizzazione)
fino a che la magnetizzazione non raggiunge il valore di saturazione M S . Ricordando che
H
B
M
0
il corrispondente valore di B è BS 0 H M M S 0 M S .
Se si aumenta ulteriormente H si trova che l’induzione aumenta come se ci si trovasse nel vuoto,
cioè si verifica
110
B 0 H
Questo perché i domini di Weiss sono ormai tutti allineati con H, dunque il materiale
ferromagnetico non può fornire più alcun contributo ulteriore all’aumento di B.
2)Se adesso si cala I, cioè H, B non ripercorre la curva di prima magnetizzazione, ma segue il
percorso sopra di essa. Questo significa che i domini di Weiss, che dovrebbero cambiare
orientamento seguendo il verso della corrente, lo fanno con ritardo rispetto alla variazione della
corrente stessa. Da questo il nome di ciclo di isteresi che viene dato alla curva, dalla parola greca
che significa ritardo. Infatti quando H=0 nel toro rimane una magnetizzazione residua M R ed il
campo di induzione vale B R . Ora il materiale è un magnete permanente.
3)Se il campo H cresce nella zona negativa fino al valore H C (campo coercitivo) la
magnetizzazione interna del materiale si riduce a zero.
4)Aumentando ancora la corrente (nel verso opposto al precedente) si ritorna alla saturazione,
questa volta con i domini orientati nel verso opposto.
5)Se la corrente applicata al toro cambia direzione periodicamente, si ottiene la curva completa
indicata in figura.
L’esistenza dell’isteresi magnetica implica che B non è una funzione univoca di H: ad ogni H
possono corrispondere infiniti valori di B a seconda del modo in cui si è pervenuti a quel valore di
H.
MATERIALI FERROMAGNETICI DOLCI E DURI. La durezza di un materiale
ferromagnetico è la sua tenedenza a rimenere nel suo stato di magnetizzazione. In pratica un
materiale ferromagnetico è tanto più duro quanto più elevato è il valore del campo magnetico
coercitivo.
I materiali ferromagnetici dolci sono impiegati là dove è necessario poter variare lo stato di
magnetizzazione degli stessi attraverso degli avvolgimenti intorno ad essi (cioè nelle macchine
elettriche).
I materiali ferromagnetici duri invece sono utilizzati come magneti permanenti per la loro virtù di
smagnetizzarsi con difficoltà.
I principali materiali ferromagnetici dolci sono
1)ferro
2)leghe ferro-nichel
3)leghe ferro-cobalto
4)leghe ferro-nichel
5)acciai a basso tenore di carbonio
PERDITE PER ISTERESI E LEGGE DI STEINMETZ. Un volume di mezzo ferromagnetico
soggetto ad una induzione variabile nel tempo con frequenza f tende a surriscaldarsi a causa della
continua riorientazione dei dominii di Weiss. Esiste a tal proposito una formula empirica, dovuta a
Steinmetz, la quale ci dice che la potenza dissipata per unità di volume di materiale ferromagnetico
sottoposto ad una induzione variabile, di frequenza f, è data da
Pist k ist BM
1, 6 2
f watt / m 3
dove è presente una costante che dipende dal mezzo.
111
CORRENTI DI FOUCAULT. Le correnti di Foucault (o correnti parassite) sono correnti
elettriche che si originano all’interno di pezzi di materiale ferromagnetico attraversati da flussi
variabili di induzione magnetica.
Si veda la figura. Un cilindro di materiale ferromagnetico è sede di una induzione variabile avente
asse parallelo a quello del cilindro stesso. L’espressione della induzione magnetica sia
Bt B M sin t k
In base alla legge di Farady-Neumann-Lenz,
considernado percorsi circolari l aventi centro in O e
raggio r, si scrive che
B
d
S
l E i dt
dove S è il cercio delimitato da l. Dunque
B
dB
B
t
d
t
S
d
S
2
2
l E i dt dt S dt 2r BM cost E r 2r BM cost
E 2rB M cost
dove E indica la componente del campo elettrico indotto tangente punto per punto alla
circonferenza di raggio r.
A tale campo elettrico è associato un campo di densità di corrente dalla legge di Ohm secondo la
relazione
J E 2rB M cost
Ricordando la legge di Joule specifica
pd
1
J
2
abbiamo che la potenza dissipata per effetto Joule in un disco di raggio R e spessore dz è data,
istante per istante, da
2 R
dzpd rdrd
0 0
2 R
dz
0 0
1
J rdrd dz
2
1
2 R
2rB
M
cost 2 rdrd
0 0
112
1
dz
4BM
2
2
2 R
2
cos t r
2
3
drd dz 4 B M
2
2
0 0
2 R
cos t r
2
3
drd
0 0
2
R
dz 4 B M 2 cos 2 t d r 3 dr dz 4 B M 2 cos 2 t
2
2
0
0
R4
2
2 dzB M 2 cos 2 t R 4 2
4
Dunque la potenza dissipata istante per istante da un disco di raggio R e di altezza L sarà
LBM 2 cos 2 t R 4 2
2
Per cui la potenza media per unità di volume dissipata istante per istante è
LB M 2 cos 2 t R 4 2
2
B M 2 cos 2 t R 2 2
2
R L
2
Facendo ora anche la media sul periodo della induzione T=2π/ω si ha
T
1
T
2
2
2
2
BM cos t R 2dt
2
0
BM
2
B M R 2
2
2
2
2
T
R t sin t cost
2
0
2
2
2
T
2
2
cos t
0
2 2
2
B M R
d t
B M R
2
2
2
T
2
cos t d t
2
0
2
2 2
sin
cos
2
0
B M 2R 2 2
2 2
2
B M R
2
2
Dunque si conclude che la potenza media dissipata per unità di tempo e di volume, a causa delle
correnti parassite è data da
Pcp 2 BM R 2 2f BM R 2 4 2f 2 BM R 2
2
2
2
2
dove si è introdotta la frequenza della induzione.
PERDITE PER CORRENTI DI FOUCAULT IN
LAMIERINI. Nel caso in cui il solido ferromagnetico sia
un lamierino la cui disposizione rispetto alla induzione
magnetica sia quella indicata in figura, e se la larghezza l è
di molto più piccola dello spessore δ, allora la potenza
media dispersa per unità di volume dal materiale è ben
espressa dalla formula
Pcp k cp f 2 BM 2
2
che è qualitativamente simile a quella calcolata precedentemente e dove si trova una costante legata
al tipo di materiale ferromagnetico in gioco.
113
PERDITE PER ISTERESI E PER CORRENTI PARASSITE NEI MATERIALI
FERROMAGNETICI. Supponiamo di avre un lamierino di materiale ferromagnetico soggetto ad
una induzione variabile con legge sinusoidale. Allora il lamierino dissipa calore sia per via delle
correnti parassite che hanno luogo al suo interno, sia per via delle perdite per isteresi.
Per quanto visto la potenza media per unità di volume dissipata è esprimibile come
Pf Pist Pcp k ist fBM
1, 6 2
k cp f 2 BM 2
2
In genere però le perdite sono riferite all’unità di peso del lamierino, piuttosto che all’unità di
volume. In effetti si trovano espresse sovente come
P | f P | ist P | cp k | ist fBM
k | ist
k ist
k | cp
k cp
1, 6 2
k | cp f 2 B M 2
2
dove ρ indica la densità del materiale.
DEFINIZIONE,
CIFRA DI PERDITA. Commercialmente ogni materiale ferromagnetico è contraddistinto dalla
cifra di perdita ovvero dalla potenza media dissipata per Kg quando
B M 1T
f 50 Hz
Nei materiali usati generalmente si ha che la cifra di perdita si attesta intorno a
0,5 3,5
W
Kg
OSSERTVAZIONE,
METODI PER RIDURRE LE PERDITE PER CORRENTI PARASSITE. Per ridurre le
perdite per correnti parassite si può operare in due modi:
1)si interviene su parametri geometrici;
2)si interviene su parametri fisici.
Il primo tipo di intervento consiste nel
realizzare il lamierino affastellando tanti
lamierini isolati. Per vedere come questo
intervento riduca la dispersione di calore a
causa di correnti parassite si considerino i due
casi indicati in figura. Per il lamierino a sx la
potenza perduta, suppenendo una dimensione
verticale L, è
114
Pcp k cp f 2 BM 2 Ll
2
Per i due lamierini affiancati a dx, se si suppongono isolati fra loro e se si suppone ancora una
dimensione verticale L, la potenza complessivamente perduta è
2
2
2
1
|
2
Ll k cp f 2 B M 2
Ll k cp f 2 B M 2
Ll Pcp
Pcp k cp f 2 B M
4
2
4
2
4
4
Insomma lo stesso volume di materiale ferromagnetico, con il semplice strataggemma di dividerlo
in due unità, dissipa quattro volte meno.
Il secondo tipo di intervento consiste nell’aumentare la resistività del lamierino, cioè ridurne la
conducibilità, visto che si era trovato, nel caso di un cilindro di raggio R, la potenza dissipata valeva
Pcp 2 BM R 2 2f BM R 2 4 2f 2 BM R 2
2
2
2
2
In genere si ottiene questo risultato usando leghe di ferro con silicio fino al 5%. Questo non riduce
significativamente le proprietà magnetiche e meccaniche del nucleo ferromagnetico, ma garantisce
una minore dissipazione di calore.
115
CAPITOLO VII,
CIRCUITI MAGNETICI
I) RILUTTANZA DEI TUBI DI FLUSSO DI B. LEGGE DI
HOPKINSON
DEFINIZIONE,
TENSIONE MAGNETICA. Definiamo tensione magnetica lungo la linea l orientata l’integrale di
linea
l H t dl
l
Si osserva che nel caso in cui la linea l sia chiusa e in cui si possano trascurare le correnti di
spostamento rispetto a quelle di conduzione si ha in particolare, per la legge di Ampère, che
l H t dl i
l
essendo i la corrente concatenata con l.
DEFINIZIONE,
PORTATA DI TUBI DI FLUSSO DELLA INDUZIONE. Consideriamo una regione di spazio in
cui sia presente un campo di induzione magnetica. Sappiamo che l’induzione magnetica è un campo
solenoidale. Questo permette di definirne un tubo di flusso e di dire che il flusso di B attraverso una
qualunque superficie che tagli ogni linea di forza del tubo di flusso (superficie tappo) è costante.
Allora definiamo portata del tubo di flusso il
flusso di B attraverso una qualunque superficie
tappo del tubo di flusso stesso. Poniamo
B n dS
St
DEFINIZIONE,
TENSIONE MAGNETICA DI TUBI DI
FLUSSO DELLA INDUZIONE. Prendiamo il
tubo di flusso di B indicato in figura. Se
supponiamo che al suo interno non vi siano
correnti di conduzione, allora
B risulta
irrotazionale (IV equazione di Maxwell in caso
stazionario). Allora la tensione magnetica fra i punti A e B non dipende dalla curva l fra essi. Se poi
le due superficie tappo S A e S B sono punto per punto ortogonali a B esse sono superficii
equipotenziali e dunque la tensione magnetica non dipende neanche da come si prendano i punti A e
B su di esse. Insomma la tensione magnetica
l H t dl
l
116
è una caratteristica del tubo di flusso, al pari della portata. Data la sua indipendenza da l si
preferisce scriverla
B
AB H t dl
A
Si ooservi sulla figura che possono adottarsi riferimenti grafici (segni + e -, freccia) per la tensione
identici a quelli usati per la tensione di tubi di flusso del campo J.
DEFINIZIONE,
RILUTTANZA DI TUBI DI FLUSSO DELLA INDUZIONE MAGNETICA. Abbiamo visto
che ad un tubo di flusso della induzione magnetica possono essere associate univocamente la
portata
B n dS
St
e la tensione magnetica
B
AB H t dl
A
(quest’ultima è definita in modo univoco se non si hanno correnti di conduzione dentro il tubo di
flusso e se quelle di spostamento sono trascurabili). Allora definiamo riluttanza del tubo di flusso il
rapporto tra la seconda e la prima. Si pone
B
AB
H t dl
A
B n dS
St
La riluttanza si misura in ampère su weber, ovvero henry alla meno uno. Si osserva che il segno
della riluttanza dipende dal segno della permebilità magnetica del materiale nel quale si sviluppa il
campo di induzione magnetica.
DEDUZIONE,
ESPRESSIONE SEMPLIFICATA DI RILUTTANZA. Nelle ipotesi che
1) B, H sono omogenei nel tubo di flusso
2) il tubo di flusso ha sezione normale costante S
allora risulta che la riluttanza del tubo di flusso è data da
l AB
S
117
dove l AB è la lunghezza dell’asse del tubo di flusso.
DIMOSTRAZIONE. Per la omogeneità di B si ha
B
BS B
H
S
S
Hdl
A
A S dl
B
B
1
dl
A
S
Ora si osservi che se B e H sono costanti ne segue che anche μ risulta costante (omogenea) e
dunque
B
1
B
dl
A
S
1
dl
A
S
l AB
S
DEDUZIONE,
RILUTTANZA DI TUBI DI FLUSSO CHIUSI: LEGGE DI HOPKINSON. I tubi di flusso
della induzione magnetica possono sempre essere prolungati finche non si chiudano su sé stessi, per
la solenoidaleità della induzione magnetica. Consideriamo allora un tubo di flusso chiso. Se
trascuriamo la corrente di spostamento abbiamo
l H t dl Ni
l
dove si è supposto che il tubo di flusso sia avvolto da N spire conduttrici attraversate da una
corrente i. Allora la riluttanza del tubo di flusso sarà
Ni
Questa formula prende il nome di legge di Hpkinson ed è del tutto analoga alla legge di Ohm se si
considerano le analogie
Ni f .e.m.
i
R
DEDUZIONE,
RELAZIONE TRA RILUTTANZA ED INDUTTANZA. Ricordando che il coefficiente di
autoinduzione delle spire che avvolgono il tubo di flusso si scrive
B
L
i
si ha
118
N
iL
i
N
e la legge di Hopkinson può scriversi anche
L
N2
L
II) NUCLEO FERROMAGNETICO
INTRODUZIONE. In un induttore toroidale con spire fittamente avvolte, così come in un
solenoide rettilineo infinito con spire fittamente avvolte, l’induzione magnetica è canalizzata, cioè
forma tubi di flusso facilmente individuabili. Nel caso di altri tipi di induttori questo non avviene e
l’induzione magnetica può formare tubi di flusso dalle forme assai complicate e dalle geometrie
molto disperse (si pensi ad esempio a quale potrebbe essere la disposizione delle linee di forza della
induzione magnetica di un solenoide a spire molto poco fitte).
Tuttavia è possibile canalizzare le linee di forza di B ricordando il significato di permeabilità
magnetica relativa del mezzo. Si ricordi che, in caso di comportamento lineare del mezzo, risulta
r 1
M
r 1
M
H
H
Dunque i mezzi con permeabilità magnetica maggiore sono quelli che, per maggiore allineamento
dei momenti magnetici interni, amplificano in misura maggiore il campo magnetico. Se dunque si
dispongono materiali ad elevata permebilità magnetica in mezzi a bassa permeabilità magnetica, si
realizza la canalizzazione della induzione all’interno dei materiali ad elevata permeabilità
magnetica.
Quanto detto lo si può vedere
meglio nel dispositivo indicato in
figura.
Abbiamo un induttore, cioè delle
spire percorse da corrente.
Abbiamo poi un toro di
permeabilità magnetica 1 . Il tutto
è immerso in un mezzo di
permeabilità
2 1
Le due linee l1 e l 2 sono della stessa lunghezza e concatenano entrambe lo stesso numero di spire,
ma una si sviluppa tutta nel toro (ne è l’asse), l’altra si sviluppa nel mezzo. Se applichiamo la legge
di Ampère ad entrambe ricaviamo
H 1l1 Ni
H1 H 2
H
l
Ni
2
2
119
dove si sono considerati i valori medi dei campi magnetici (è un discorso molto grossolano). Ma
allora
H1 H 2
B1
1
B2
2
B1
B2
1
1 B 1 B 2
2
Insomma l’induzione magnetica sarà, grosso modo, tutta nel toro di materiale ad alta permeabilità.
I materiali ad alta permeabilità per eccellenza sono i materiali ferromagnetci. L’aria si può
considerare, al confronto, un mezzo a bassissima permeabilità (vedi tabelle).
DEFINIZIONE,
NUCLEO FERROMAGNETICO. Nei circuiti magnetici si dice nucleo ferromagnetico l’insieme
di pezzi, costituiti da materiale ferromagnetico, usati per canalizzare l’induzione magnetica.
DEFINIZIONE,
TRAFERRO. I nuclei ferromagnetici, per esigenze costruttive, possono presentare delle
discontinuità. Queste discontinuità sono riempite di mezzi amagnetici (in genere aria) e prendono il
nome di traferri. Le parti ferromagnetiche che delimitano un traferro sono dette espansioni polari.
DEDUZIONE,
RIFRAZIONE DELLA INDUZIONE MAGNETICA AL TRAFERRO. Risulta che la
induzione magnetica al traferro è quasi ortogonale alla superficie delle espansioni polari, qualunque
sia l’angolo con il quale l’induzione proveniente dal materiale ferromagnetico incide sulla
superficie di separazione col traferro.
Inoltre l’induzione rientra nel nucleo ferromagnetico con lo stesso angolo, rispetto alla normale alla
superficie, che aveva prima del traferro.
DIMOSTRAZIONE. Si consideri
l’illustrazione e si ricordi la legge di
rifrazione della induzione magnetica
nelle superficie di separazione fra
mezzi (capitolo 6) la quale afferma
che
tan 2 2
tan 1 1
tan 2 2
tan
1
dove è stata applicata alle due superficie di separazione che contengono il traferro. Adesso
consideriamo la prima delle due espressioni e osserviamo che
2
1
1
tan 2 tan 1 2 1
2
tan
tan 1
2
1
Ciò prova la prima parte della tesi, tenendo presente che in media
120
2
10 4
1
Ora si consideri anche la legge di rifrazione applicata alla secondo superficie di separazione, quella
che dal traferro riporta al materiale ferromagnetico. Si ha
2
tan 2 2
tan tan 2 tan 1
1
1
1
tan 1 2 tan 1 tan 1 1
2 1
tan 2 2 tan 1 tan
2
1
2
tan
Ciò prova la restante parte della tesi.
OSSERVAZIONE,
SPESSORE DEL TRAFERRO. Anche se, come visto, quando l’induzione entra nel traferro non
devia di molto dalla normale alla superficie di separazione, è tuttavia evidente che traferri molto
spessi porteranno ad una fuoriuscita di flusso di induzione. In altre parole minore è lo spessore del
traferro e minore è la perdita di flusso di induzione al rientro nel nucleo ferromagnetico.
DEDUZIONE,
RILUTTANZA DEL TRAFERRO. Considerando lo spazio occupato dal traferro come un tratto
di tubo di flusso di induzione magnetica allora si può associare al traferro stesso una riluttanza
t
0 S
dove t è lo spessore del traferro, S è la sua sezione e dove la sua permeabilità magnetica è stata
sostituita con quella del vuoto.
DEDUZIONE,
ENERGIA MAGNETICA DEL TRAFERRO. Ricordando che la densità di energia in una
regione di spazio sede di una induzione magnetica è data da (capitolo 5)
u
1 B2
2
allora l’energia magnetica nello spazio occupato da un traferro di spessore t e sezione S è
U
1 B2
St
2
DEDUZIONE,
PRESSIONE MAGNETICA AL TRAFERRO. Se l’energia magnetica che compete al traferro è
data da
U
1 B2
St
2
121
allora le due facce delle espansioni polari tenederanno ad avvicinarsi per ridurre tale energia
riducendo lo spessore t del traferro. In particolare la forza attrattiva che esercitano reciprocamente è
U
1 B2
F
S
t
2
In pratica dunque sulle facce delle espansioni polari si esercita una pressione negativa data da
P
1 B2
2
dove si può anche considerare la permeabilità magnetica del vuoto, visto che il traferro è fatto di un
mezzo amagnetico la cui permeabilità magnetica relativa è dunque prossima alla unità.
III) CIRCUITI MAGNETICI
INTRODUZIONE. Esaminiamo le analogie tra il campo di induzione magnetica B in condizioni
stazionarie o quasi-stazionarie6 ed il campo di densità di corrente J in condizioni stazionarie.
1)Per la densità di corrente in condizioni stazionarie la legge di continuità porge
div J 0
Per la induzione magnetica in condizioni generiche la terza equazione di Maxwell porge
div B 0
Entrambi i campi sono cioè solenoidali: hanno linee di forza chiuse e hanno tubi di flusso che
conservano la portata (portata che per J è la corrente i, mentre per B è il flusso Ф).
2)Per la densità di corrente in condizioni stazionarie la legge di Ohm in piccolo porge
J E c E g V E g J V E g E g f .e.m.
dove γ è la conducibilità del materiale.
Per la induzione magnetica in condizioni stazionarie o quasi stazionarie (vedi nota 1) la legge di
Ampère porge
B
1
Ni
1
f .m.m.
dove si è anticipata la definizione di forza magneto motrice (f.m.m.) che sarà data nel seguito.
6
Le condizioni quasi-stazionarie sono quelle in cui si può trascurare l’effetto della corrente di spostamento e
dunque si può applicare la legge di Ampère
H Ni .
122
3)Il flusso di J viene canalizzato con l’uso di materiali a bassa conducibilità γ. Il flusso di B viene
canalizzato con mezzi a bassa permeabilità magnetica.
DEFINIZIONE,
CIRCUITO MAGNETICO. Alla luce delle analogie di cui sopra, come un campo di densità di
corrente costituisce un circuito elettrico (o rete elettrica), così un campo di induzione ben
canalizzato è detto circuito magnetico (o rete magnetica). Esso è costituito da materiali
ferromagnetici che realizzano tubi di flusso di B, caratterizzati
1)dalla riluttanza;
2)dalle amperspire prodotte da spire attraversate da corrente avvolte intorno ai materiali
ferromagnetici.
OSSERVAZIONE,
IMPIEGO DEI CIRCUITI MAGNETICI. I circuiti magnetici sono impiegati
1)per canalizzare il flusso della induzione prodotta da due avvolgimenti (trasformatori);
2)per realizzare una determinata induzione in un certo punto dello spazio (motori).
DEFINIZIONE,
FORZA MAGNETOMOTRICE. La legge di Hopkinson afferma, come visto, che, se si considera
un tubo di flusso chiuso avente riluttanza , portata e un avvolgimento di N spire attraversate
dalla corrente i, allora
Ni
L’analogia di questa espressione con la formula
f .e.m. iR
relativa ad un circuito costituito da una sola
maglia avente resistenza R, corrente i e forza
elettromotrice f.e.m., porta alla definizione di
forza magneto motrice come il prodotto Ni. Si
pone
f .m.m. Ni
Ora, se la f.e.m. è un lavoro per unità di carica, la f.m.m. ha le dimensioni di ampère, cioè di una
corrente. Comunque non è una forza, proprio come la f.e.m..
Si osserva un’analogia per quanto riguarda i riferimenti. Nei generatori elettrici il riferimento di
corrente rispetto al quale, in un circuito semplice come quello in figura, la corrente è positiva è
quello che va dal segno più al segno meno. Nei generatori di forza magneto motrice il riferimento di
flusso rispetto al quale il flusso è positivo (sempre nel caso del circuito magnetico elementare in
figura) è quello che vede la corrente delle spire correre in senso antiorario).
Cioè in entrambi i casi il riferimento del generatore determina il riferimento di flusso (di corrente)
rispetto al quale il flusso (la corrente) è positivo.
123
DEDUZIONE,
PRIMA LEGGE DI KIRCHHOFF PER CIRCUITI MAGNETICI. Supponiamo di avere un
circuito magnetico ramificato. Prendiamo in considerazione un nodo di tale sistema, ovvero un
punto del circuito in cui convergono più tubi di flusso. Allora la solenoidalità di B ci permette di
affermare che la somma dei flussi uscenti da una superficie chiusa S delimitante il nodo deve essere
nulla. Cioè
i
0
in cui i flussi con riferimento uscente da S vanno
sommati, vanno sottratti quelli con riferimento
entrante.
DEDUZIONE,
SECONDA LEGGE DI KIRCHHOFF PER I
CIRCUITI MAGNETICI. Se la prima legge di
Kirchhoff per circuiti magnetici deriva dalla solenoidaleità di B (terza legge di Maxwell), la
seconda legge di Kirchhoff per circuiti magnetici deriva dalla legge di Ampère, ovvero dalla quarta
equazione di Maxwell in caso stazionario. Dunque tale legge vale solo in caso stazionari o quasi
stazionario (effetti magnetici delle correnti di spostamento trascurabili). Allora la legge di Ampère
ci dice che presa comunque una maglia della rete
magnetica la circuitazione di B è
B Ni
Ricordando
magnetica
poi
la
definizione
di
tensione
B
AB H t dl
A
si perviene alla seconda legge di Kirchhoff per
circuiti magnetici
Ni
i
i
Per specificare meglio tale legge si osservi che: fissato un verso di percorrenza positivo della maglia
(in modo arbitrario) è fissati i riferimenti di tensione dei tubi di flusso allora
1)le tensioni vengono sommate se percorse dal + al –;
2)le tensioni vengono sottratte se percorse da – a +;
3)le forze magnetomotrici vengono sommate se il verso positivo arbitrario della maglia vede le loro
correnti scorrere in senso antiorario;
4)le forze magnetomotrici vengono sottratte se il verso positivo arbitrario della maglia vede le loro
correnti scorrere in senso orario.
Nel caso dunque della maglia indicata in figura si avrà
124
N 1i1 N 2 i2 N 3i3
ANALISI DEI CIRCUITI MAGNETICI. Come visto sin qui l’analisi dei circuiti magnetici è
simile a quella dei circuiti elettrici. Tuttavia è necessario rilevare che la dipendenza della
permeabilità magnetica del nucleo con i valori della induzione che in esso ha sede rende tutto più
complicato. Infatti se la riluttanza di un tratto di tubo di flusso, come si è visto, si esprime
l
S
è evidente che non le si potrà assegnare un valore finchè non sia noto il valore del campo di
induzione in quel tratto di tubo di flusso. D’altra parte il valore della induzione (del suo flusso),
note le f.m.m., dipende dalle riluttanze. Dunque? Si usano allora metodi numerici da assegnare al
calcolatore.
125
APPENDICE I,
SINTESI GENERALE
CAPITOLO I,
ELETTROSTATICA NEL VUOTO
COSTANTE DIELETTRICA DEL VUOTO
0 8.85 10 12
C2
Nm2
CAMPO ELETTRICO DI UNA CARICA PUNTIFORME NEL VUOTO
1 q r
E 0 r
4 0 r 2 r
PRIMA EQUAZIONE DI MAXWELL IN CONDIZIONI STAZIONARIE NEL VUOTO
0
div E 0
SECONDA EQUAZIONE DI MAXWELL IN CONDIZIONI STAZIONARIE NEL VUOTO
rot E 0 0
POTENZIALE ELETTRICO NEL VUOTO DI UNA CARICA PUNTIFORME
E 0 P V0 P V0 P
1
q
40 r P
DIPOLO ELETTRICO
E 0 x P
p 3xz
4 0 r 5
p 3 yz
E 0 y P
4 0 r 5
E 0 z P
p 3z 2 r 2
4 0
r5
V 0 P
p r
4 0 r 3
1
126
CAPITOLO II,
IL CAMPO ELETTROSTATICO IN PRESENZA DI
MATERIA
CAMPO ELETTRICO SULLA SUPERFICIE DI UN CONDUTTORE NEL VUOTO
E 0 P
0
VETTORE INTENSITA’ DI POLARIZZAZIONE
P
N p
V
CARICHE DI POLARIZZAZIONE
pol P n
pol div P
VETTORE SPOSTAMENTO ELETTRICO
D 0 E P
SUSCETTIVITA’ DIELETTRICA IN UN DIELETTRICO ISOTROPO
P
0 E
0
COSTANTE DIELETTRICA RELATIVA IN UN DIELETTRICO ISOTROPO
r 1 1
PRIMA E SECONDA EQUAZIONE DI MAXWELL NEI DIELETTRICI.
PRIMA EQUAZIONE DI MAXWELL
SECONDA
EQUAZIONE DI
MAXWELL
CASO GENERALE
div 0 E P lib div D lib
rot E 0
ISOTROPIA
div r 0 E lib div E lib div D lib
rot E 0
127
ISOTROPIA E
OMOGENEITA’
div E
lib
div E lib div D lib
0 r
rot E 0
SUPERFICIE DI SEPARAZIONE FRA DUE MEZZI
E t1 E t 2
Dn1 Dn 2
tan 1 1r
tan 2 2 r
CAMPO ELETTRICO
DIELETTRICO
DI
UNA
CARICA
PUNTIFORME
IMMERSA
IN
UN
1 q r
E r
2
4 r r
CAPACITA’ DEL CONDUTTORE ISOLATO
C
Q
V
CAPACITA’ DEL CONDENSATORE SFERICO
C0
0 S1 S 2
d
S1 S 2
C
d
CAPACITA’ DEL CONDENSATORE PIANO
C0
0S
d
S
C
d
ENERGIA POTENZIALE ELETTRICA DI UN CONEDENSATORE
1
1 Q2
2
U 0 C V0
2
2 C
DENSITA’ DI ENERGIA POTENZIALE IN UN CAMPO ELETTRICO
1
u P E 2 P
2
128
CAPITOLO III,
CORRENTE ELETTRICA E SORGENTI DI FORZA
ELETTROMOTRICE
LEGAME TRA DENSITA’ DI CORRENTE ELETTRICA E INTENSITA’ DI CORRENTE
ELETTRICA
i t J P, t n P dS
S
LEGGE DI CONTINUITA’
div J P, t
P, t J x P, t J y P, t J z P, t
P, t
t
y
z
t
x
TABELLA RIASSUNTIVA
ELETTROCINETICA
CAMPO ELETTRICO
E P, t E c P, t E i P, t
POTENZIALE ELETTRICO
Non definito non essendo il campo elettrico
conservativo
J P, t E P, t
POSTULATO DI OHM
p d P J P , t J P , t
POSTULATO DI JOULE
P, t
div J P, t
t
CONSERVAZIONE DELLA CARICA
ELETTROCINETICA STAZIONARIA
E P E c P V (P)
CAMPO ELETTRICO
E i ( P) 0
2V P, t 0
POTENZIALE ELETTRICO
POSTULATO DI OHM
POSTULATO DI JOULE
CONSERVAZIONE DELLA CARICA
V ( P) E P E c P
J P E c P V P
p d J P J P
P
div J P
0
t
129
POTENZA DISSIPATA DA UN TRONCO
DI TUBO DI FLUSSO DI J
B
Pd UI E c P t dl J P ndS
A
S
B
RESISTENZA DI UN TRONCO DI TUBO
DI FLUSSO DI J
R
U
I
E c P t dl
A
J P ndS
S
CAPITOLO IV,
FENOMENI MAGNETICI
VUOTO
STAZIONARI
NEL
FORZA MAGNETICA FRA CARICHE IN MOTO
r r
2 1
q 2 V2 q1 V1
r2 r1
F0 r2 0
2
4
r2 r1
CAMPO DI UNA CARICA IN MOTO
V r
B0 0 q 3
4
r
PRIMA FORMULA DI LAPLACE
dB0
0 dl r
i 3
4
r
FORZA DI LORENTZ
F0 q V B 0
SECONDA FORMULA DI LAPLACE
d F0 i dl B 0
PERMEABILITA’ MAGNETICA DEL VUOTO
0 4 10 7
Wb
Am
LEGGE DI AMPERE
B 0 0 i
SECONDA EQUAZIONE DI MAXWELL IN CONDIZIONI STAZIONARIE NEL VUOTO
div B0 0
TERZA EQUAZIONE DI MAXWELL IN CONDIZIONI STAZIONARIE NEL VUOTO
130
rot B 0 P 0 J P
L’INDUZIONE DI UN FILO RETTILINEO INFINITO (LEGGE DI BIOT-SAVART)
0i
B 0 P
2 OP
0 0
INDUZIONE SULL’ASSE DI UNA SPIRA CIRCOLARE
0 iR 2
B 0 z 0 0
3
2
z
INDUZIONE SULL’ASSE DI UN SOLENOIDE TOROIDALE
B0
0 Ni
2 r 2R2
2
TEOREMA DI EQUIVALENZA DI AMPERE
DIPOLO ELETTRICO
DIPOLO MAGNETICO
POTENZIALE SCALARE DETERMINATO A GRANDE DISTANZA
p r
V 0 P
4 0 r 3
1
m r
U 0 P 0 3
4 r
CAMPO DETERMINATO A GRANDE DISTANZA
E 0 x P
p 3xz
4 0 r 5
p 3 yz
E 0 y P
4 0 r 5
E 0 z P
p 3z 2 r 2
4 0
r5
0 3xz
m 5
4
r
0 3 yz
B0 y P
m 5
4
r
0 3z 2 r 2
B 0 z P
m
4
r5
B0 x P
SOLLECITAZIONE AGENTE SUL DIPOLO IMMERSO IN UN CAMPO
UNIFORME
F 0
F 0
p E 0
m B 0
CAPITOLO V,
CAMPI ELETTRICI E MAGNETICI DIPENDENTI
DAL TEMPO
LEGGE DI FARADAY-NEUMANN-LENZ
131
B
d
S
d
B
S n dS
E
i
l
dt
dt
SECONDA EQUAZIONE DI MAXWELL NEI CASI NON STAZIONARI
B
P
rot E i P
rot v P B P
t
FORZA ELETTROMOTRICE AUTOINDOTTA, COEFFICIENTE DI AUTOINDUZIONE
f .e.m. i L
d
i t
dt
B
L
i
ENERGIA POTENZIALE MAGNETICA DI UNA INDUTTANZA
U
1 2
Li
2
DENSITA’ DI ENERGIA DEL CAMPO DI INDUZIONE MAGNETICA
1 B 0 P
u 0 P
2 0
2
CIRCUITI ACCOPPIATI
di1
di 2
f .e.m.1 L1 dt M dt R1i1
f .e.m. L di 2 M di1 R i
2
2
2 2
dt
dt
ENERGIA POTENZIALE MAGNETICA DEI CIRCUITI ACCOPPIATI
U
1
1 I1 2 I 2
2
QUARTA EQUAZIONE DI MAXWELL IN CASI NON STAZIONARI
DP, t
rot H P, t J P, t
t
132
CAPITOLO VI,
FENOMENI
MAGNETICI
PRESENZA DI MATERIA
STAZIONARI
IN
VETTORE INTENSITA’ DI MAGNETIZZAZIONE
N m
M
V
CORRENTI ATOMICHE
J at rot M
VETTORE CAMPO MAGNETICO
B
H
0
M
SUSCETTIVITA’ MAGNETICA IN UN MEZZO ISOTROPO
M
H
PERMEABILITA’ MAGNETICA RELATIVA DI UN MEZZO ISOTROPO
r 1
TERZA E QUARTA EQUAZIONE DI MAXWELL NEI DIELETTRICI.
TERZA EQUAZIONE
DI MAXWELL
CASO GENERALE
QUARTA EQUAZIONE DI MAXWELL
B
0 M
rot
J
rot
H
J
0
div B 0
ISOTROPIA
div B 0
ISOTROPIA E
OMOGENEITA’
B
rot
0 r
div B 0
rot B
0 r
J rot B j rot H
J
J
rot B
j rot H J
SUPERFICI DI SEPARAZIONE FRA DUE MEZZI
133
Bn1 Bn 2
H t1 H t 2
tan 1 r1 0
tan 2 r 2 0
134
APPENDICE II,
LE QUATTRO EQUAZIONI DI MAXWELL
CASO GENERALE (PRESENZA DI MEZZO GENERICO)
EQUAZIONE
CASO NON STAZIONARIO
CASO STAZIONARIO
I
div 0 E P lib
div 0 E P lib
div D lib
div D lib
II
B
rot E
t
III
div B 0
rot E 0
div B 0
B
0 M D
rot
J t
0
IV
D
rot H J
t
B
0 M
rot
J
0
rot H J
CASO LINEARE (PRESENZA DI MEZZO ISOTROPO)
P 0 r 1 E D E
M r 1 H H B
EQUAZIONE
I
CASO NON STAZIONARIO
CASO STAZIONARIO
div E lib
div E lib
div D lib
div D lib
II
B
rot E
t
III
div B 0
rot E 0
div B 0
135
B
E
rot J
t
IV
B
rot J
E
rot H J
t
CASO LINEARE OMOGENEO
ISOTROPO OMOGENEO)
rot H J
(PRESENZA
DI
MEZZO
P 0 r 1 E D E
M r 1 H H B
r è una costante spaziale
r è una costante spaziale
EQUAZIONE
I
CASO NON STAZIONARIO
div E lib
div D lib
div D lib
II
B
rot E
t
III
div B 0
IV
E
rot B J
t
rot E 0
div B 0
E
rot H J
t
CASO STAZIONARIO
div E lib
rot B J
rot H J
In particolare se il mezzo isotropo omogeneo è il vuoto allora
r 1
r 1
e dunque
136
EQUAZIONE
CASO NON STAZIONARIO
div E 0 lib
0
I
CASO STAZIONARIO
div E 0 lib
0
div D lib
div D lib
II
B0
rot E 0
t
III
div B0 0
IV
E0
rot B0 0 J 0 0
t
rot E 0 0
E0
rot H J 0
t
div B0 0
rot B0 0 J
rot H J
137
APPENDICE III,
LE UNITA’ DI MISURA DEL SISTEMA
INTERNAZIONALE
I) IL SISTEMA INTERNAZIONALE DI UNITA’
Il sistema internazionale di unità è il sistema adottato dalla Conférence Générale des Poids et
Mesures e da convenzioni internazionali. Esso consta di sette unità di base e di due unità
supplementari adimensionate.
Nella tabella seguente sono elencate le nove grandezze e le relative unità di misura. La definizione
di ciascuna delle nove unità di misura è fornita nel dettaglio nel seguito.
UNITA’ DI MISURA
GRANDEZZA
Lunghezza
Massa
Intervallo di tempo
Intensità di corrente elettrica
Temperatura termodinamica
Quantità di sostanza
Intensità luminosa
Angolo piano
Angolo solido
metro
kilogrammo
secondo
ampère
kelvin
mole
candela
UNITA’ ADIMENSIONATE
radiante
steradiante
SIMBOLO DELLA
UNITA’ DI MISURA
m
kg
s
A
K
mol
Cd
rad
sr
DEFINIZIONE,
METRO. E’ la lunghezza percorsa dalla luce nel vuoto in un intervallo di tempo della durata di
1
s
299792458
(delibera della 17° riunione, 1983).
DEFINIZIONE,
KILOGRAMMO. E’ pari alla massa del prototipo conservato al Pavillon de Breteuil (Sèvres)
(delibera della prima riunione, 1889). Un campione di massa è presente anche in Italia presso il
Ministero dell’Industria, a Roma.
DEFINIZIONE,
INTERVALLO DI TEMPO. E’ la durata di 9192631770 di periodi della radiazione
corrispondente alla transizione tra i due livelli iperfini dello stato fondamentale dell’atomo di cesio
133 (delibera della 13° riunione, 1976).
DEFINIZIONE,
AMPERE. E’ l’intensità di corrente costante che, attraversando due conduttori
1)rettilinei e paralleli
2)di lunghezza infinita e spessore trascurabile
138
3)posti alla distanza di un metro nel vuoto
produce una forza (attrattiva o repulsiva) fra i conduttori di
2 10 7 N
metro
(delibera della 9° riunione, 1948). In Italia è presente un dispositivo del genere presso l’Istituto
Elettrotecnico Galileo Ferraris, a Torino.
DEFINIZIONE,
KELVIN. E’ la frazione 1 273,15 della temperatura termodinamica del punto triplo dell’acqua
(delibera della 13° riunione, 1967). E’ stato stabilito che il kelvin va usato sia per esprimere la
temperatura termodinamica, che per esprimere un intervallo di temperatura. In Italia la scla
termodinamica della temperatura può essere costruita a partire da campioni presso l’Istituto di
Metrologia Colonnetti del C.N.R. di Torino.
DEFINIZIONE,
MOLE. Una mole è una quantità di entità (atomi, molecole, ioni, elettroni etc.) di numero pari al
numero di atomi di carbonio 12 presenti in 0,012 kg di carbonio 12 (delibera della 14° riunione,
1971).
DEFINIZIONE,
CANDELA. E’ l’intensità luminosa, in una data direzione, di una sorgente che emette una
radiazione monocromatica di frequenza pari a
540 1012 hertz
la cui intensità di radiazione in quella direzione sia di
1
watt
683 steradiante
(delibera della 16° riunione, 1979).
DEFINIZIONE,
RADIANTE.
E’
l’ampiezza
dell’angolo piano α che intercetta sulla
circonferenza un arco lungo quanto il
raggio della circonferenza stessa (vedi
figura).
DEFINIZIONE,
STERADIANTE. E’ l’ampiezza
dell’angolo solido Ω che intercetta
sulla sfera una calotta di area uguale a
quella del quadrato il cui lato ha la
lunghezza del raggio (vedi figura).
139
II) UNITA’ DI MISURA DERIVATE
Nella tabella seguente indichiamo alcune delle grandezze derivate più comuni, le loro unità di
misura e l’espressione di queste in termini delle nove unità di misura fondamentali, introdotte nel
paragrafo precedente, e anche in termini di altre unità di misura (derivate e non).
GRANDEZZA
UNITA’ DI
MISURA
SIMBOLO
frequenza
hertz
Hz
forza
newton
N
pressione
pascal
Pa
joule
J
coulomb
C
volt
energia, lavoro,
calore
carica elettrica
differenza di
potenziale, forza
elettromotrice,
tensione
ESPRESSIONE IN
TERMINI DI
UNITA’ DI MISURA
FONDAMENTALI
ESPRESSIONE IN
TERMINI DI
ALTRE UNITA’ DI
MISURA
s 1
m kg
s2
kg
ms 2
m 2 kg
s2
A s
N J
,
m2 m3
V
m 2 kg
A s3
W J
,
A C
A2 s 4
m 2 kg
C
V
kg m 2
s 3 A2
s 3 A2
kg m 2
kg
s2 A
V
A
J
m
N m
capacità elettrica
farad
F
resistenza
elettrica
ohm
Ω
conduttanza
siemens
S
tesla
T
weber
Wb
kg m 2
s2 A
V s
henry
H
kg m 2
s 2 A2
Wb
A
induzione
magnetica
flusso di
induzione
magnetica
induttanza
1 A
,
V
Wb
m2
OSSERVAZIONE,
CONVENZIONI SUI NOMI DELLE UNITA’ DI MISURA. Per i nomi delle unità di misura si
seguono le regole qui indicate.
1) I nomi delle unità di misura sono sempre minuscoli, anche quando derivano da quelli di uno
scienziato;
2) se il nome di una unità di misura deriva da quello di uno scienziato allora il simbolo della unità
va maiuscolo;
3) se il nome di una unità di misura non deriva da quello di uno scienziato, allora il simbolo della
unità va minuscolo.
L’unica eccezione a queste regole è la unità di misura candela il cui simbolo è maiuscolo pur non
derivando il suo nome da quello di uno scienziato.
140
APPENDICE IV,
COSTANTI
CARICA DELL’ELETTRONE
e 1.6 10 19 C
COSTANTE DIELETTRICA DEL VUOTO
0 8.85 10
12
C2
Nm2
PERMEABILITA’ MAGNETICA DEL VUOTO
0 4 10 7
Wb
Am
141
APPENDICE V,
OPERATORI VETTORIALI NEI DIVERSI SITEMI
DI RIFERIMENTO.
COORDINATE CILINDRICHE
FIGURA DI RIFERIMENTO
LEGAME TRA COORDINATE CARTESIANE E COORDINATE CILINDRICHE
r x 2 y 2 1
2x
r cos
cos
1
x
2 2
r
2 2
x
x y
r x 2 y 2 1
2y
r sin
sin
r x 2 y 2
1
y
y
2
r
2
2
x y 2
x r cos
y
y r sin arctan
1
y
x2
y
y
sin
x
2
2
2
2
2
2
2
z z
x
x y x
x y
r
y x
z z
1
x
1
1
x2 1
x
cos
2
2
2
2
2
y
r
y x x y x x y
1
x
LEGAME TRA VERSORI
cos
i
sin
j
i
cos
sin
sin i cos j j sin cos
k k
k k
142
LEGAME TRA DERIVATE
f f r f
x r x
f f r f
y r y
f z f
f sin
cos
x z x r
r
f z f
f cos
sin
y z y r
r
LEGAME TRA COMPONENTI
Fx F i Fr Fs Fz k i Fr i Fs i Fz k i Fr cos sin
Fs cos sin Fz k cos sin Fr cos Fs sin
Fy F j Fr Fs Fz k j Fr j Fs j Fz k j Fr sin cos
Fs sin cos Fz k sin cos Fr sin Fs cos
Fz Fz
GRADIENTE IN COORDINATE CILINDRICHE
f f f f
f sin f
f cos f
i
j
k cos
k
i sin
j
x
y
z
r r
r
z
r
f
f sin
f sin sin cos
cos cos sin
cos sin
r
r
r
f cos
f k f cos 2 f sin cos f sin cos
sin cos
r
r
r
r
z
f
f sin 2 f
f
f sin cos f cos 2 f
2
sin sin cos
k
r
r
r
r
r
z
f
f 1
f
k
r
r
z
DIVERGENZA IN COORDINATE CILINDRICHE
div F
Fy cos Fz
Fx Fy Fz Fx
F sin Fy
cos x
sin
x
y
z r
r r
r z
Fr cos Fs sin sin
Fr cos Fs sin
cos
r
r
Fr sin Fs cos cos Fz
Fr sin Fs cos
sin
r
r z
143
F
F
F
1 F
1
1
1
r cos 2 s sin cos r sin cos s sin 2 Fr sin 2 Fs sin cos
r
r
r
r
r
r
F
F
F
1 F
1
1
1 F
r sin 2 s sin cos r sin cos s cos 2 Fr cos 2 Fs sin cos z
r
r
r
r
r z
r
F
F
F
1 F
1 F
1
r cos 2 s sin 2 r sin 2 s cos 2 z Fr
r r
r z
r
r
F 1 Fs Fz
1 1 rFr 1 Fs Fz
r
Fr
r r
z
r r r
r
z
LAPLACIANO IN COORDINATE CILINDRICHE
f
f
y
f f f
2 f
x
2 f 2 2 2 2
x
y
z
x
y
z
2
2
2
f
f
f sin
f sin
cos
cos
r
r
r
r sin
cos
r
r
f
f
f cos
f cos
sin
sin
r
r
r
r cos 2 f
sin
2
r
r
z
2
2
2
2
f
f sin cos f
f
f sin f cos sin
2 cos 2
cos sin
r
r
r
2 r
r r
r
r
2 f
2 f sin cos 2 f
f
2 f cos f sin cos 2 f
2 sin 2
sin
cos
2
r
r
r
2 r
r r
z
r
r
2 f
2 f sin cos 2 f sin cos f sin 2 2 f sin 2 f sin cos
2 cos 2
r
r
r
r r
2 r 2
r2
r
r
2 f
2 f sin cos 2 f sin cos f cos 2 2 f cos 2 f sin cos
2 sin 2
2
2
2
r
r
r
r
r
r
r
r
r
f
r
2
2
2
2
f f 1 f
1 f f 1 r 1 2 f 2 f
2 2
2
2
z
r
r r r 2 z 2 r r
r 2 z 2
ROTORE IN COORDINATE CILINDRICHE
i
rot F
x
Fx
j
y
Fy
k
Fz Fr sin Fs cos Fr cos Fs sin Fz
i
j
z y
z
z
x
Fz
144
Fr sin Fs cos Fr cos Fs sin
k
x
y
F
F
F
sin
cos
i
z r sin s cos Fr
Fs
z
z
z
z
y
F
cos
sin Fz
F
r cos s sin Fr
Fs
j
z
z
z
x
z
F
F
F
sin
cos Fr
cos
sin
k
r sin s cos Fr
Fs
cos s sin Fr
Fs
x
x
x
y
y
y
y
x
F
F
F F
F
F
z r sin s cos i r cos s sin z j
z
z
z
x
y
z
F
F
F
sin cos
sin 2 Fr
sin cos
cos 2
k
r sin s cos Fr
Fs
cos s sin Fr
Fs
x
r
r
y
y
r
r
x
F
F
F F
F
F
z r sin s cos i r cos s sin z j
z
z
z
x
y
z
F
F
F
1 F
r sin s cos Fs r cos s sin k
x
r y
y
x
F
F F
z r sin s cos cos sin
z
z
y
F
F
F
r cos s sin z sin cos
z
x
z
F
F
F
F
r sin s cos r cos s sin Fs
x
y
y
x
F
F
F
z cos r sin cos s cos 2
z
z
y
1
k
r
F
F
F
z sin r sin 2 s sin cos
z
z
y
F
F
F
r sin cos s sin 2 z sin
z
x
z
F
F
F
r cos 2 s sin cos z cos
z
x
z
F
F
F
F
1
r sin s cos r cos s sin Fs k
x
y
y
r
x
F
F
F cos
F
z sin z
cos r sin cos s cos 2
r
z
z
r
F
F
F cos
F
z sin z
sin r sin 2 s sin cos
r
z
z
r
145
F
F
F
F sin
r sin cos s sin 2 z cos z
sin
z
r
r
z
F
F
F
F sin
r cos 2 s sin cos z cos z
cos
z
r
r
z
F
F sin
F
F sin
r cos r
sin s cos s
cos k
r
r
r
r
F
F cos
F
F cos
r sin r
cos s sin s
sin Fs
r
r
r
r
1
k
r
F
F
F cos 2 Fr
z sin cos z
sin cos s cos 2
r
z
z
r
F
F
F sin cos Fr
z sin 2 z
sin 2 s sin cos
r
z
z
r
F
F
F
F sin 2
r sin cos s sin 2 z sin cos z
z
r
r
z
F
F
F
F sin cos
r cos 2 s sin cos z cos 2 z
z
r
r
z
2
F
F sin cos
F sin Fs
k
r sin cos r
cos 2 s
r
r
r
r
F
F sin cos
F cos 2 Fs
r sin cos r
sin 2 s
Fs
r
r
r
r
1 Fz Fs Fz Fr Fs 1 Fr
1
Fs k
z
z
r
r
r
r r
1
k
r
1 Fz Fs Fr Fz 1 rFs Fr
k
z
r
r r
z
r
COORDINATE SFERICHE
FIGURA DI
RIFERIMENTO
146
GRADIENTE IN COORDINATE POLARI
f
f f f f
1 f 1 f
i
j
k
k
x
y
z
r
r sin
r
DIVERERGENZA IN COORDINATE POLARI
div F
Fx Fy Fz
1 r 2 Fr
1 Fs
1 sin Ft
2
x
y
z
r r
r sin r sin
ROTORE IN COORDINATE POLARI
i
rot F
x
Fx
j
y
Fy
k
1 Fs sin Ft
z r sin
Fz
1 rFt Fr
r r
1 Fr r sin Fs
r sin
r
LAPLACIANO IN COORDINATE CILINDRICHE
f
f
r 2
sin
2
f f f
1 r
1
f
1
2
f 2 2 2 2
2 2
x
y
z
r
r
r sin 2 r 2 sin
2
2
2
147