Corsi di Laurea in Ingegneria
Prova scritta di Fisica Generale 1 (Prof. G. Naletto)
Corsi estivi a Bressanone - Bressanone, 9 Agosto 2013
Cognome .............................................................. Nome ........................................... Matricola .......................
Docente di riferimento a Padova: Prof. ...................................................................
Problema 1
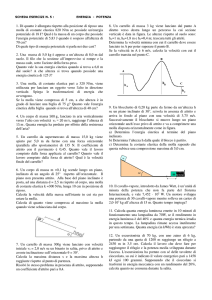
Un corpo di dimensioni trascurabili e massa m = 1.2 kg inizialmente
fermo
su un piano orizzontale scabro, viene messo in moto all’istante
m J
M
to = 0 grazie all’applicazione di un impulso di modulo J. Dopo un tempo
t = 5 s, il corpo esce dal piano scabro con velocità di modulo v = 1 m/s e
“sale” su un carrello di massa M = 10 kg, posto allo stesso livello del
piano e inizialmente fermo. Il coefficiente di attrito dinamico tra corpo e piano scabro è µd = 0.15, mentre non c’è attrito
tra corpo e carrello e tra carrello e piano orizzontale sottostante il carrello stesso. All’estremo del carrello opposto a
quello da cui è entrato il corpo è vincolata una molla ideale a riposo di costante elastica k posta orizzontale e orientata
lungo la traiettoria del moto del corpo. Proseguendo il suo moto sul carrello, il corpo urta la molla che si comprime al
massimo di ∆xmax = 0.08 m. Determinare:
a) il modulo J dell’impulso applicato inizialmente al corpo;
b) il valore k della costante elastica della molla.
Problema 2
B
A
2θ
m
lo
lo
Un corpo di dimensioni trascurabili e massa m = 1.5 kg si trova all’interno di una cavità
rettangolare verticale di larghezza 2lo = 0.5 m. Il corpo è inizialmente fermo, soggetto
all’azione combinata di due molle ideali identiche vincolate in modo simmetrico nei punti A
e B alle pareti laterali della cavità e di un filo teso verticale collegato al corpo e al punto
centrale del fondo della cavità (vedi figura). Le due molle hanno lunghezza a riposo pari a
lo (metà della larghezza della cavità), costante elastica k = 150 N/m; inizialmente sono
allungate entrambe di ∆l (quindi la loro lunghezza totale iniziale è l = l o + ∆l) e l’angolo
tra le due molle è 2θ = 60°. Ad un certo istante si taglia il filo ed il corpo si mette in
movimento verso l’alto. Determinare:
a) il modulo T della tensione del filo;
b) il modulo v della velocità del corpo quando si trova alla stessa altezza dei punti A e B.
Problema 3
Due lastre rettangolari omogenee identiche A e B di massa m = 3 kg sono vincolate a
ruotare senza attrito attorno all’asse z, sovrapposto ad un loro lato; il lato delle lastre
perpendicolare
all’asse z ha lunghezza l = 0.4 m. Il sistema, inizialmente fermo, viene
B
messo in rotazione dall’azione di un motore applicato all’asse z che imprime un momento
B
A
di modulo M = 0.5 Nm; quando il sistema ha compiuto una rotazione ∆θ = 3π rad, si stacca
A
il motore. Ad un istante successivo, agendo solo tramite forze interne al sistema, le due
l
l
l
l
lastre si allontanano dall’asse di rotazione spostandosi di una distanza l lungo due guide
perpendicolari all’asse z di massa trascurabile (vedi figura di destra); a conclusione di
questo spostamento, si trova che il sistema delle due lastre ruota con velocità angolare ω’. A questo punto, una delle due
lastre urta in modo anelastico un piolo vincolato al pavimento e il sistema delle due lastre si mette in rotazione nel verso
opposto con una velocità angolare di modulo ω” = 9 ω’/10. Determinare:
a) il modulo ω della velocità angolare del sistema quando si stacca il motore;
b) il modulo ω’ della velocità angolare del sistema subito dopo che le lastre si sono allontanate dall’asse z;
c) il numero N di volte che, in totale, il sistema delle due lastre urta contro il piolo, nell’ipotesi che l’energia dissipata
ad ogni urto sia sempre la stessa.
z
z
Problema 4
Tre moli di un gas ideale biatomico si trovano inizialmente in equilibrio nello stato A. Tramite una espansione isobara
reversibile, il gas si porta nello stato di equilibrio B. Successivamente, tramite una trasformazione adiabatica irreversibile
in cui il gas varia la sua energia interna di ∆UBC = –3000 J, il gas si porta nello stato C. Infine, per mezzo di una
trasformazione isoterma reversibile in cui scambia con l’ambiente un calore QCA = –3600 J, il gas ritorna nello stato A.
Sapendo che il rapporto tra i volumi occupati dal gas negli stati A e C è VA/VC = 0.6, determinare:
a) il valore TB della temperatura del gas in B;
b) il rendimento η del ciclo.
Problema 5a (per chi ha in programma il secondo principio della termodinamica)
Una macchina termica reversibile assorbe calore da un cilindro a pistone mobile contenente una miscela di acqua e
vapore alla temperatura T2 = 373.15 K (temperatura di ebollizione dell’acqua) e cede calore ad una miscela di acqua e
ghiaccio alla temperatura T1 = 273.15 K (temperatura di fusione del ghiaccio). La miscela di acqua e vapore, grazie al
pistone mobile, è sempre in equilibrio con la pressione ambiente esterna pext = 105 Pa e, per un ciclo della macchina,
l’ambiente compie un lavoro Wext = 200 J su questa miscela. Il lavoro prodotto dalla macchina serve a comprimere un gas
ideale a temperatura costante T = 300 K. Sapendo che il calore latente di ebollizione dell’acqua è λv = 2.26⋅106 J/kg, che
quello di fusione del ghiaccio è λg = 3.3⋅105 J/kg, che la densità del vapor acqueo a T2 è ρv = 0.58 kg/m3 (e che quella
dell’acqua è ρa = 103 kg/m3), e assumendo che le quantità di vapore e di ghiaccio nelle due miscele siano sufficienti a
mantenerle alle temperature di ebollizione dell’acqua e di fusione del ghiaccio rispettivamente, determinare:
a) la massa di ghiaccio mg che fonde ad ogni ciclo della macchina termica;
b) la variazione ∆S di entropia del sistema termodinamico costituito dalla macchina termica, dalle due miscele e dal gas
ideale, per un ciclo della macchina.
Problema 5b (per chi non ha in programma il secondo principio della termodinamica)
Un corpo di dimensioni trascurabili e massa m = 1.5 kg è inizialmente fermo su un
piano orizzontale scabro (coefficiente di attrito dinamico tra corpo e piano µd = 0.1)
appoggiato ad una molla ideale di costante elastica k = 750 N/m tenuta compressa. Ad
m
un certo istante si sblocca la molla, la quale mette in moto il corpo. Dopo aver percorso
R
sul piano scabro una distanza l = 1.1 m dalla posizione iniziale, il corpo ha una velocità
di modulo v = 0.8 m/s; in quell’istante, il corpo incontra nel suo moto una guida liscia
di massa M = 5 kg posta tangenzialmente al moto del corpo che lo vincola a percorrere una traiettoria orizzontale
circolare di raggio di curvatura R = 0.6 m. Determinare:
a) la compressione iniziale ∆x della molla;
b) il valore minimo µs,min del coefficiente di attrito statico tra piano scabro e guida tale da tenere ferma la guida stessa.
Soluzioni
Problema 1
a)
b)
J
− µ d gt ⇒ J = m(v + µ d gt ) = 10.0 Ns
m
Nell’istante di massima compressione della molla, il corpo ha velocità nulla rispetto al carrello e quindi corpo e
carrello hanno istantaneamente la stessa velocità, coincidente con la velocità del centro di massa.
m
v
mv = mv'+mV ' = (m + M )vCM ⇒ vCM =
m+ M
v(t ) = vo + at =
1 2 1
1
1 m2
1
2
mv = (m + M )vCM
+ k∆x 2 =
v 2 + k∆x 2
2
2
2
2 m+ M
2
∆Em = 0 ⇒
⇒ k=
1 mM 2
v = 167 N/m
∆x 2 m + M
Problema 2
a)
b)
1
∆l = l − l o = l o
− 1 = 0.25 m; Fel = k∆l ⇒ T = 2 Fel vert − mg = 2k∆l cosθ − mg = 50.3 N
sin θ
Quando il corpo si trova alla stessa altezza dei punti A e B, le due molle sono nella situazione di lunghezza a riposo.
E m ,i = E m, f
⇒
1
1
1
2 ⋅ k∆l 2 = mgh + mv 2 = mg l cos θ + mv 2
2
2
2
⇒
v=
2k 2
cos θ
∆l − 2 gl o
= 2 m/s
m
sin θ
Problema 3
1
2
I z = 2 ⋅ ml 2 = ml 2
3
3
a)
M = I z α;
b)
2
1
3 14
I ' z = 2 m l 2 + m l =
ml 2 ;
2 3
12
c)
E diss = E ' k − E " k =
α =
⇒
M
3M
=
;
Iz
2ml 2
I zω = I ' z ω '
⇒
1
1
1
I ' z ω ' 2 − I ' z ω " 2 = I ' z ω ' 2 −ω " 2
2
2
2
ω 2 = 2α ∆ θ
⇒
ω=
3M
ml 2
∆ θ = 5 .43 rad/s
2
ml 2
Iz
1
3
ω' =
ω=
ω = ω = 0. 775 rad/s
14
I 'z
7
ml 2
3
E 'k
100
ω'2
⇒
=
=
= 5 .3 ⇒ N = 6
2
2
E diss
19
ω ' −ω "
Problema 4
p
QCA = WCA = nRTC ln
a)
A
B
VA
VC
⇒ TC = TA =
QCA
= 282.6 K;
V
nR ln A
VC
QBC = 0; ∆U BC = −WBC = ncV (TC − TB ) ⇒ TB = TC −
C
∆U BC
= 330.7 K
ncV
Q AB = nc P (TB − TA ) = 4200 J; W AB = nR(TB − TA ) = 1200 J
b)
V
η=
W + WBC + WCA
W
= AB
= 0.143
Q ASS
Q AB
Problema 5a
a)
b)
m
m p m
W ρ
Wext = − p ext ∆ Vmisc = − p ext Vacqua − V v = − p ext a − v ≈ ext v ⇒ m v = ext v = 1.16 ⋅ 10 −3 kg
p ext
ρ
ρ
ρ
v
v
a
−mg λg
λ T
T
Q
Q1 Q2 −mg λ g − mv λv
ηR = 1 − 1 = 1 + 1 = 1 +
; oppure
+
=
+
= 0 ⇒ mg = mv v 1 = 5.82 ⋅ 10−3 kg
T2
Q2
− mv λv
T1 T2
T1
T2
λg T2
(
)
La macchina e le due miscele hanno una variazione complessiva nulla di entropia, in quanto si tratta di un universo
termodinamico che compie delle trasformazioni reversibili. Quindi, la variazione di entropia è solo dovuta al gas
ideale che compie la trasformazione isoterma reversibile.
− m g λ g + mv λ v
Q
Q + Q2
Q1 + Q2 = W = −Wisot = − Qisot ⇒ ∆S = isot = − 1
=−
= −2.34 J/K
T
T
T
Problema 5b
a)
b)
(
)
1
1
m 2
⇒ − µ d mgl = mv 2 − k∆x 2 ⇒ ∆x =
v + 2µ d gl = 0.075 m
2
2
k
La guida esercita sul corpo una reazione corrispondente alla forza centripeta Fcp; per il principio di azione e
reazione, quindi, anche il corpo esercita sulla guida la stessa forza in modulo ma con verso opposto (centrifugo).
Affinché la guida non si muova, la forza di attrito statico deve uguagliare in modulo questa forza.
Wnc = ∆Em
Fcp = m
v2
= −Fguida ⇒
R
f as = Fguida = m
v2
mv 2
≤ f as,max = µ s N = µ s (m + M )g ⇒ µ s ≥
= 0.025
(m + M )gR
R