4 I Condensatori
4.1 Struttura dei condensatori
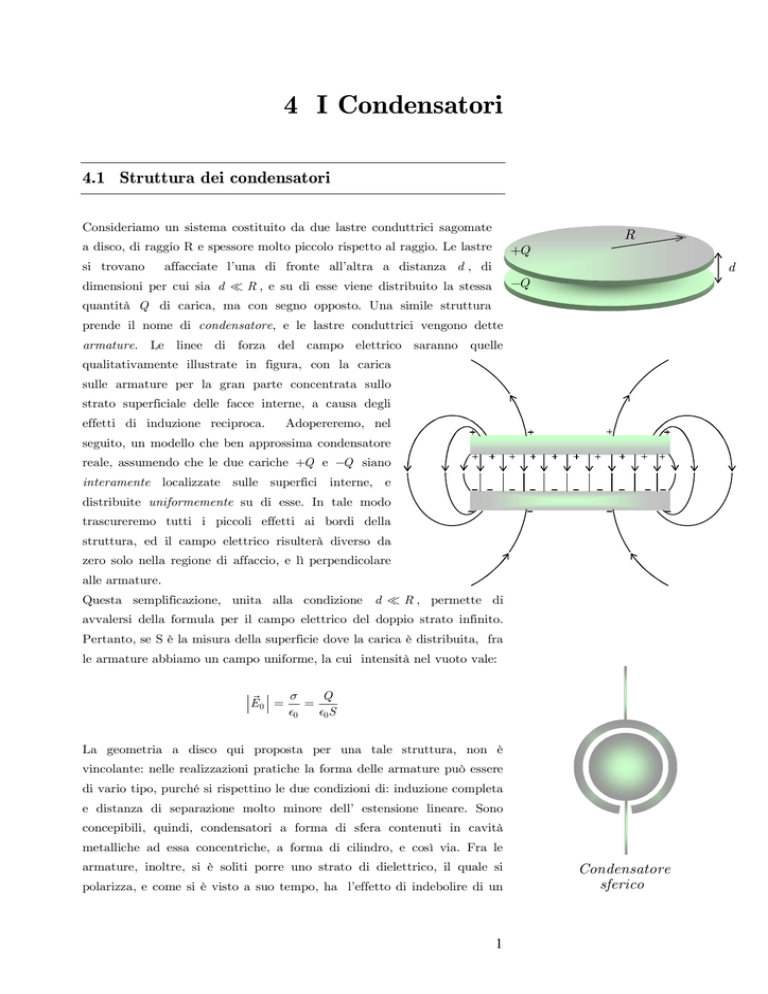
Consideriamo un sistema costituito da due lastre conduttrici sagomate
R
a disco, di raggio R e spessore molto piccolo rispetto al raggio. Le lastre
si trovano
Q
affacciate l’una di fronte all’altra a distanza d , di
d
Q
dimensioni per cui sia d R , e su di esse viene distribuito la stessa
quantità Q di carica, ma con segno opposto. Una simile struttura
prende il nome di condensatore, e le lastre conduttrici vengono dette
armature. Le linee di forza del campo elettrico saranno quelle
qualitativamente illustrate in figura, con la carica
sulle armature per la gran parte concentrata sullo
strato superficiale delle facce interne, a causa degli
effetti di induzione reciproca.
Adopereremo, nel
seguito, un modello che ben approssima condensatore
reale, assumendo che le due cariche Q e Q siano
interamente localizzate sulle superfici interne, e
distribuite uniformemente su di esse. In tale modo
trascureremo tutti i piccoli effetti ai bordi della
struttura, ed il campo elettrico risulterà diverso da
zero solo nella regione di affaccio, e lì perpendicolare
alle armature.
Questa semplificazione, unita alla condizione d R , permette di
avvalersi della formula per il campo elettrico del doppio strato infinito.
Pertanto, se S è la misura della superficie dove la carica è distribuita, fra
le armature abbiamo un campo uniforme, la cui intensità nel vuoto vale:
Q
E0
0
0S
La geometria a disco qui proposta per una tale struttura, non è
vincolante: nelle realizzazioni pratiche la forma delle armature può essere
di vario tipo, purché si rispettino le due condizioni di: induzione completa
e distanza di separazione molto minore dell’ estensione lineare. Sono
concepibili, quindi, condensatori a forma di sfera contenuti in cavità
metalliche ad essa concentriche, a forma di cilindro, e così via. Fra le
armature, inoltre, si è soliti porre uno strato di dielettrico, il quale si
polarizza, e come si è visto a suo tempo, ha l’effetto di indebolire di un
1
Condensatore
sferico
fattore
1
, a parità di carica localizzata, il valore del campo E nello
r
Regione
Neutra
spazio interposto. Infatti la tendenza delle molecole del dielettrico, a
deformarsi od allinearsi lungo la direzione del campo, lascia neutra la
regione interna e produce l’equivalente di uno strato superficiale di carica.
Questo origina un campo aggiuntivo E p che si sovrappone, con direzione
opposta, ad E 0 , riducendo l’intensità del campo risultante:
E E 0 E p . Se lo spazio di separazione è omogeneamente riempito, si
che, indipendentemente dalla carica Q
E0
localizzata sulle armature, il rapporto r è legato unicamente al
E
osserva sperimentalmente
tipo di materiale dielettrico utilizzato. Il valore numerico di questo
rapporto, r 1 , prende il nome di costante dielettrica del mezzo. Fra le
armature avremo quindi un campo di intensità:
E0
E
.
r
0r
E dielettrico
E armature
La realizzazione pratica di un condensatore a facce piane parallele fa uso
di alcuni accorgimenti tecnici, come quello di utilizzare per armature delle
sottili strisce metalliche separate da pellicole isolanti. La struttura viene
avvolta a rotolo, come in figura, e si presenta a forma di piccolo cilindro.
Si costruiscono anche condensatori in cui una delle due armature è
costituita da una soluzione liquida o gelatinosa, generalmente di
tetraborato di sodio, detti condensatori elettrolitici. La configurazione è
quella di un involucro cilindrico di alluminio, contenente la soluzione
elettrolitica, ed al centro un altro conduttore cilindrico di alluminio.
Intorno a quest’ultimo, immerso nella soluzione, attraverso un opportuno
passaggio di carica si fa formare un sottile strato di bollicine di idrogeno.
Questo sottilissimo strato fa depositare sul conduttore interno dell’ossido
di alluminio, che riveste il ruolo del dielettrico per questo tipo di
Conduttore
condensatore. L’involucro e la soluzione possono quindi essere caricati
Isolante
negativamente, mentre il conduttore interno fa da armatura positiva.
Ossido
di Al
soluzione
elettrolitica
4.2 L’energia potenziale dei condensatori
1. Proprietà generali
Un condensatore è un sistema di due conduttori carichi, ed in quanto tale
possiede energia potenziale elettrostatica. Come sappiamo, essa è definita
come pari al lavoro svolto dal campo elettrostatico quando si smembra la
2
Condensatore
elettrolitico
configurazione di cariche in eccesso su ciascuna delle armature
separandole fino a distanza infinita1. Poiché tuttavia, al termine dello
smembramento, avremo due lastre conduttrici neutre affacciate, il fatto
che la forza elettrostatica
sia conservativa ci autorizza a dire che il
lavoro svolto dal campo durante qualunque processo che conduca ad un
tale stato finale è sempre pari all’energia potenziale del sistema. Pertanto
si è soliti parlare di energia potenziale elettrostatica del condensatore
come lavoro svolto dal campo elettrico durante il passaggio della carica in
eccesso sull’armatura positiva a quella sull’armatura negativa. Un tale
processo è detto anche scarica del condensatore; dato che la scarica è
agevolata dalle forze del campo, l’energia potenziale di un condensatore è
positiva.
UN
CONDENSATORE È QUINDI UN DISPOSITIVO IN GRADO DI
ACCUMULARE ENERGIA POTENZIALE ELETTROSTATICA
lo si dovrà immaginare come una molla compressa, in grado di rilasciare
la sua energia allungandosi di scatto non appena gliene venga data
l’opportunità. Un condensatore si dice pertanto carico quando vi è stata
incamerata energia potenziale. Si faccia pertanto attenzione all’ambiguità
del termine carico, che, in questo caso, non si riferisce ad una
localizzazione di carica elettrica. In effetti un condensatore non
accumula carica, dato che nel complesso si tratta di un oggetto
neutro: la sua carica complessiva è Q Q 0 . Un modello di
condensatore che si rifà all’idraulica
viene proposto qui a lato.
Supponiamo che all’interno di una conduttura piena di acqua vi sia
una camera cilindrica con un setto separatore connesso con delle
molle. Tale dispositivo blocca lo scorrimento
dell’acqua
al suo
interno, e può, in un certo senso, essere caricato. Comprimendo la
prima
molla
in
una
qualunque
delle
due
direzioni,
e
conseguentemente estendendo l’altra, il condensatore incamera
energia potenziale, che è in grado di rilasciare
spingendo l’acqua
attraverso un tubo di uscita. Se, poi, questo tubo è collegato all’altro in
ingresso in una sorta di circuito, allo svuotamento di una regione
corrisponderà il riempimento dell’altra, e durante il processo si avrà una
violenta scarica di acqua nelle condutture. Al termine, il dispositivo sarà
riempito esattamente dello stesso quantitativo di acqua che conteneva
inizialmente, ma la sua energia potenziale sarà scesa a zero.
1
Per portare all’infinito le cariche positive senza distruggere il reticolo dell’armatura
possiamo immaginare che la lastra metallica si vada estendendo infinitamente, di modo che
gli ammanchi di elettroni si disperdano su di essa a distanza infinita le une dalle altre.
3
Il condensatore torna utile tutte le volte che si ha bisogno di una sorta di
molla elettrica: ovvero di produrre un intenso flusso di cariche che
scorrano in un tempo brevissimo. Nei dispositivi di
defibrillazione del
cuore, ad esempio si fa ampio uso di tale proprietà, così come nei flash
delle macchine fotografiche.
Calcoleremo ora la proprietà di incamerare energia in relazione alla carica
che poniamo su una delle due armature. Indichiamo con V il potenziale
dell’armatura carica positivamente e con V
quello dell’armatura
negativa affacciata.
2. La capacità dei condensatori
Definiamo prima una nuova grandezza fisica che descrive il condensatore
esprimendo quanta carica Q si deve porre sull’armatura positiva (e
quindi quanta Q
sulla negativa) per ogni Volt di differenza di
potenziale che si desidera stabilire. Si tratta del rapporto:
C
Il numero C
Q
Q
V
V V
viene detto capacità del condensatore, e dipende
innanzitutto dalla geometria e dal dielettrico interposto fra le armature.
Ci chiediamo ora: dipende pure da Q e V ? A ben pensarci la capacità
risulterebbe essere un parametro utile solo nel caso in cui fosse del tutto
indipendente da Q e V . In questo caso infatti il quantitativo di carica
da porre sulle armature per avere ogni Volt di differenza di potenziale
non dipenderebbe né dalla carica già ivi presente né dalla differenza di
potenziale già stabilita, ma sarebbe una costante, caratteristica di quel
condensatore. Come utilità assomiglierebbe in un certo senso alla
resistenza, che è indipendente dalla tensione applicata e dalla corrente
presente, come stabilito dalla legge di Ohm.
Dimostriamo quindi che la capacità è una costante caratteristica solo
della geometria e del dielettrico interposto, attraverso una catena di
ragionamenti.
1. La geometria del condensatore costringe le cariche a distribuirsi in
modo uniforme sulle due facce affiancate.
2. Se quindi Q aumenta di un certo fattore, di quello stesso fattore
aumenta (essendo fissata la superficie).
3. Ne segue che del medesimo fattore cresce E
0
.
V
V
4. Essendo E
, e rimanendo fissa la distanza d fra le
s
d
armature, anche V cresce nel medesimo rapporto.
4
Ne concludiamo che la capacità di un condensatore (lontano da influenze
esterne) è una costante: raddoppiando la carica Q raddoppia V ,
triplicandola triplica, e così via.
3. Calcolo della capacità di un condensatore piano
A titolo di esempio calcoliamo la capacità di un condensatore piano con
armature di area S , separate da una distanza d .
Abbiamo visto che la diminuzione di potenziale spostandosi lungo le linee
di forza, che vanno dall’armatura positiva quella negativa, vale
V V | E | d . Si ricava quindi:
V V
| E |
d
Ma sappiamo anche che fra le armature il campo elettrico è costante, e
pari a
E
(| E |
nel caso di dielettrico interposto).
0
0r
d
Confrontando otteniamo V V
, che sostituito nella formula per
0
C fornisce:
C
Q
S
Q
0 0
V V
d
d
Q
. Se vi è un dielettrico interposto, ripetendo
S
S
i passaggi la formula cambia in: C 0 r , evidenziando come il
d
dielettrico accresca il valore della capacità, essendo sempre r 1 .
dove si è sfruttato che
V (t )
4. Calcolo dell’energia immagazzinata nel condensatore
La conservatività della forza elettrostatica ci consente di immaginare un
qualunque processo per caricare le armature e calcolare l’energia
potenziale della configurazione ottenuta per questa via: in ogni caso il
risultato è
identico visto che il lavoro non dipende dalla traiettoria
seguita.
Supponiamo quindi di partire dalle due armature neutre e di spostare di
volta in volta un certo quantitativo di carica Q 0 dall’armatura che
diventerà negativa a quella che diventerà positiva. Sarà un po’ come
scavare una buca nel suolo per costruire una collina con la terra estratta.
Ad ogni spostamento di Q si ha un incremento pari a U nell’energia
potenziale del condensatore, pari a:
5
V (t )
Q
U U fin U in Q[V (t ) V (t )]
Se volessimo calcolare l’energia potenziale finale, quando sulle armature
abbiamo posto complessivamente la carica Q e fra di esse si è stabilita la
differenza di potenziale V dovremmo addizionare tutti questi U :
U U 1 U 2 ...
Ma in ognuno dei U viene contemplata una differenza di potenziale
V (t ) V (t ) che cresce ad ogni nuova aggiunta di carica, proprio come
la collina di terra sale di livello ad ogni aggiunta di materiale, ed ogni
volta dobbiamo faticare un po’ di più per portarla fino in cima. Infatti
ogni nuova carica positiva Q strappata rende l’armatura negativa un
poco più negativa, così da opporsi di più alla successiva estrazione.
Analogamente ogni aggiunta di Q sull’armatura positiva la rende un
poco più positiva, così da opporsi maggiormente al successivo inserimento.
E’ insomma come una strana scala i cui gradini aumentano ad ogni nostro
passo. Ma se raffiguriamo nel piano Q(t ) (carica sulle armature al tempo
V
V (t )
Q(t)
C
Vfin
t), V (t ) (differenza di potenziale fra le armature al tempo t) la relazione
che definisce la capacità:
V (t )
Q(t )
V (t )
C
otteniamo una retta di coefficiente angolare 1 . Come si vede, in questo
C
piano ogni incremento di energia U corrisponde all’area del rettangolo
sotteso
dalla
retta,
di
base
Q
ed
altezza
V (t ) .
L’energia
complessivamente incamerata sarà pertanto l’intera area del triangolo
evidenziato in giallo di base Qfin ed altezza Vfin , quelli che finora
abbiamo chiamato semplicemente Q e V , cioè rispettivamente la carica
depositata sulle armature e la differenza di potenziale raggiunta.
Si ottiene:
1
Q2
1
U QV
CV 2
2
2C
2
Esempio 1
Il flash di una macchina fotografica è alimentato dalla scarica di un
condensatore di capacità C 400 F caricato ad una differenza di
potenziale fra le armature V V 300 V . L’energia rilasciata vale:
1
1
U CV 2 (400 106 )(300)2 6.00 J
2
2
6
0
Q
Q(t )
Qfin
Q(t ) Q
Q
Esempio 2
La fibrillazione ventricolare
è una contrazione del cuore in modo
scoordinato. Poiché i muscoli sono delle macchine elettriche, è possibile
ristabilire la normalità attraverso il rapido passaggio di carica prodotto
dalla scarica di un condensatore.
capacità
C 175 F
e
che
Sapendo che il condensatore ha
viene
caricato
con
un’energia
di
U 400 J possiamo risalire alla differenza di potenziale fra le sue
armature:
1
CV 2 400 J
2
V
2 400
175 106
2000 V
5. La densità di energia del campo elettrico
Quando una regione di spazio è sede di un campo elettrico significa che è
stato compiuto del lavoro per distribuire le cariche nella configurazione
che a tale campo dà luogo. Ad esempio lo spazio fra le armature di un
condensatore è sede di un campo elettrico costante e per produrlo si è
dovuto lavorare contro il campo elettrico al fine di separare le cariche
che originano il campo e disporle sulle armature. Da un punto di vista
matematico è comodo pensare che questa energia la si trova distribuita
nella regione di spazio che è sede del campo, e quindi risulta utile
associare una densità di energia ad ogni punto. Attenzione però che
stiamo parlando solo di una comodità matematica, che non va presa alla
lettera.
L’energia è una grandezza fisica associata all’interazione fra
oggetti, e misura la capacità di produrre lavoro del sistema di corpi in
questione2. Non esiste, nemmeno in linea di principio, dell’energia
separata dagli oggetti che interagiscono. Quindi non bisogna immaginare
l’energia come effettivamente localizzata nello spazio, ma piuttosto
parliamo di densità di energia intendendo con essa uno strumento per
poter eseguire dei calcoli. Nota infatti la densità di energia, basterà
moltiplicarla per il volume ove è localizzato il campo elettrico (ad esempio
lo spazio fra le armature) per avere l’energia complessiva.
Indicata quindi con u l’energia per unità di
volume, il condensatore
piano di area A e distanza di separazione d ne consente agevolmente il
calcolo come segue:
densità di energia u
2
1 QV
energia
2
volume
d A
La definizione di energia come “capacità di eseguire lavoro (in condizioni ideali)” ha senso
se riferita ad un sistema e non ad un singolo oggetto.
7
Esprimiamo ora u in funzione del campo elettrico. Si ricavano le
relazioni:
E
Q
0
A0
E
V
d
Q 0AE
V Ed
Che inserite nell’espressione per u forniscono:
u
1 QV
1 0 AE E d
1
0 E 2
2 dA
2
2
dA
Abbiamo così mostrato che in una regione di spazio sede di campo
elettrico E costante, ad ogni metro cubo risulta associato un quantitativo
1
0E 2 . Questa espressione è del tutto generale e non
2
dipende dal fatto che sia stata ricavata nel particolare caso di un
di energia pari a
condensatore piano. Se infatti accadesse che la densità di energia dovuta
ad una distribuzione di cariche che generano un campo di valore E , fosse
dipendente da come sono disposte le cariche che lo producono,
significherebbe che il campo elettrico non conterrebbe informazioni
sufficienti per descrivere le proprietà fisiche di quella regione di spazio. Il
campo elettrico sarebbe un concetto sbagliato ed inutile se, per ipotesi, in
una regione sede di un valore di E identico a quello fra le armature del
condensatore, ma originato da una distribuzione di cariche puntiformi, si
avesse una diversa densità di energia.
1
0 E 2 vale nel
2
caso di campo costante: se l’intensità di E
Chiaramente l’espressione u
Volume 1
cambia da punto a punto, come vicino ad una
u1
carica puntiforme, dovremo suddividere lo spazio
1
2
0 E 12
in tanti cubetti all’interno dei quali il campo si
può considerare costante, applicare la formula
Volume 2
1
0 E 2 in ognuno di essi e poi fare la somma
2
su tutto lo spazio.
u
u2
1
1
Vol 1 0E12 Vol 2 0E22 ...
totale
2
2
energia
8
1
2
0 E 2 2
4.3 Il processo di carica e scarica del condensatore
Scopo del presente capitolo è ricavare un’espressione analitica per la
corrente in un circuito contenente un condensatore ed una resistenza
1
durante il processo di carica e poi durante quello di scarica.
Analizziamo il circuito a lato tenendo presente che nella realtà i
portatori di carica sono gli elettroni, ma per semplicità si assume
che la corrente sia dovuta allo spostamento di cariche positive
fittizie che si muovono in verso opposto a quello degli elettroni.
ε
1. Quando l’interruttore viene portato nella posizione 1, sopra
all’armatura collegata con il polo positivo del generatore si
-
-
C
depositano cariche positive perché essa si trova a potenziale
inferiore. Contemporaneamente
altre cariche positive si staccano dalla
seconda armatura per portarsi sul polo negativo del generatore, che si
trova a potenziale minore dell’armatura.
2. In realtà il circuito è interrotto dal condensatore, quindi durante questo
processo non sta circolando carica. Se infatti considero una superficie fra
le armature del condensatore essa non è attraversata da nessuna
particella. Tuttavia per ogni portatore che giunge sull’armatura positiva,
ce n’é uno che si stacca da quella negativa e quindi tutto va come se il
circuito fosse chiuso.
3. Col procedere del depositarsi di nuove cariche positive sull’armatura
“+” le nuove arrivate vengono respinte da quelle già presenti ed
analogamente quelle positive che desiderano lasciare
1
R
l’armatura “-“ sono trattenute dall’eccesso di cariche
negative che lì si è formato. Il processo rallenta
progressivamente, per arrestarsi quando le due armature
si sono portate al potenziale dei rispettivi poli del
generatore e fra di esse si è riprodotta la fem
ε
del
ε
i(t )
generatore.
4. Per rappresentare il fatto che filo e contatti elettrici
offrono resistenza alla corrente, rendiamo realistico il circuito inserendo
R nel disegno. Come vedremo, la possibilità di variarne il valore
permette di controllare il processo di carica.
5. Indichiamo con Q(t ) la quantità di carica che dall’istante t 0 in cui
l’interruttore è stato girato, fino all’istante t , è passata attraverso una
sezione del filo. Si tratta, evidentemente, dello stesso quantitativo di
carica depositato sull’armatura positiva del condensatore. Durante il
processo abbiamo visto che tutto va come se ci fosse corrente, ma non
possiamo utilizzare la definizione data per i circuiti in corrente continua
(CC) dato che l’espressione:
9
C VC (t )
I
Q
t
pari al rapporto fra la carica Q che attraversa una sezione del filo
nell’intervallo t e t , non è più un valore costante, ma contiene la
grandezza variabile:
Q Q(t t ) Q(t )
Infatti se le nuove cariche in arrivo sono sempre più ostacolate da quelle
presenti, la quantità di carica Q che attraversa la sezione del filo del
circuito durante t , diminuisce col passare del tempo.
Posso tuttavia generalizzare la definizione di corrente considerando un
intervallo infinitesimo, cioè:
i(t ) lim
t 0
Q(t t ) Q(t )
Q
lim
Q (t )
t
0
t
t
Con questo procedimento si definisce una funzione a valori in ogni istante
pari al rapporto fra l’infinitesimo quantitativo di carica che passa nella
sezione
ed
il
tempuscolo
infinitesimo
durante
il
quale
passa.
Sinteticamente si dice che la corrente è “la derivata della carica rispetto
al tempo”.
6. Indichiamo ora con VC (t ) V V la differenza, variabile nel tempo,
fra il potenziale dell’armatura positiva e quello dell’armatura negativa ed
applichiamo la legge delle maglie di Kirchhoff partendo dal polo negativo
del generatore. Si ha:
ε Ri(t ) VC (t ) 0
Q(t )
è una grandezza costante, caratteristica
VC (t )
Sappiamo che il rapporto
del condensatore, cioè dipendente solo dalla sua geometria e dai materiali
adoperati, ma non dalla quantità di carica depositata né dal tempo
Q(t )
trascorso. Abbiamo allora VC (t )
. Inserendo le relazioni per la
C
corrente e la differenza di potenziale si ha:
ε RQ (t ) QC(t ) 0
CRQ (t )
εC Q(t )
Q (t )
1
Q(t ) C
RC
ε
7. Un’equazione come quella sopra scritta si dice equazione differenziale,
in quanto la sua incognita non è un numero, ma è una funzione, Q(t ) , e
contiene la derivata di tale funzione, cioè Q '(t ) . Per risolverla osserviamo
10
che la grandezza
Q (t )
è la derivata della funzione
Q(t ) C
ε
ln[Q(t ) C ]
ε
1
rispetto al tempo. A secondo membro c’è invece la costante RC
. La
1
1
funzione che, derivata, produce RC
come risultato è RC
t . Nel caso
più generale dobbiamo tenere conto della possibilità che ci fosse anche
una costante k scomparsa nella derivazione:
ε
D ln[Q(t ) C ]
1
RC
Q(t ) εC e
k t RC
ε
ln[Q(t ) C ]
ek e
t RC
Ae
t
k
RC
t RC
avendo indicato con A il valore costante e k .
8. Sapendo poi che all’inizio la carica sulle armature è nulla, cioè
Q(0) 0 , imponendo questa condizione si trova A εC , che sostituito
produce:
Q(t ) εC Ae
t RC
ε
Q(t ) C (1 e
Ricordando poi che i(t ) Q (t ) e che VC (t )
i(t )
ε e t RC
)
Q(t )
otteniamo:
C
VC (t ) ε(1 e
R
t RC
t RC
)
9. Rappresentiamo graficamente gli andamenti di Q , V ed i in funzione
del tempo:
i(t )
Q(t )
VC (t )
ε
εC
ε
R
lim i(t ) 0
lim Q(t ) εC
lim VC (t ) ε
t
t
t
t
t
t
10. La costante RC , legata alla pendenza, ha le dimensioni di un
tempo:
F
V C C
s
A V C/s
11
e si dice costante di tempo del circuito. Se ad esempio C 100 µF ,
R 220 kΩ risulta:
RC 220 103 100 106 22 s
Q(t )
Maggiore è il valore di RC meno ripide risultano le curve Q(t ) ,
VC (t ) ed i(t ) , come si evince calcolandone la derivata. La costante
RC
rappresenta infatti il tempo che occorre alla carica sul
condensatore per raggiungere il 63.2% del suo valore massimo
ε
Q( ) C (1 e
RC
ε
grande
ε
) C (1 e 1 ) 0.632 C
potenziale fra le armature per raggiungere il 63.2% del suo massimo
t
ε.
Quando t la corrente i(t ) è invece scesa al 36.8% del valore
ε/R . Anche se il tempo ideale di carica è infinito si osserva che
il condensatore è quasi completamente carico per t 4 . Questa
discrepanza con la teoria si spiega ricordando che tutta la procedura ha
fatto uso
piccolo
εC :
oppure, analogamente, esprime il tempo che occorre alla differenza di
iniziale
εC
VC (t )
ε
0.90ε
0.63ε
ε
0.10
dall’approssimazione secondo la quale l’intera carica delle
armature del condensatore si dispone solo sulle superfici affacciate delle
4
t
i(t )
armature, trascurando gli effetti al bordo. Ciò ha avuto il grande
ε I
vantaggio di consentire di introdurre la capacità del condensatore come
R
una costante, ed ora ci presenta il piccolo prezzo da pagare in termini di
max
imprecisione nel tempo di carica complessivo.
11. Con un ragionamento analogo al precedente è possibile ricavare
l’andamento della corrente in un circuito nel quale il condensatore si
scarichi, come quello qua sotto riportato:
R
2
i(t ) C
-
-
0.37I max
VC
Una volta escluso il generatore, e chiuso l’interruttore nella posizione 2 in
figura, il condensatore funge da generatore tentando di riportare le
cariche positive in eccesso su di un’armatura a bilanciare quelle negative
in eccesso sull’altra. Il processo funziona un po’ come quando si rilascia
12
t
una molla compressa. Si può dimostrare che durante questo processo,
la carica sulle armature del condensatore Q(t ) e la
detto di scarica,
corrente nel circuito decrescono secondo le leggi:
Q(t ) εCe
t RC
i(t )
ε e t RC
R
dove il segno meno in i(t ) indica solo
un
verso
opposto
precedente
rispetto
corrente
di
alla
Q(t )
i(t )
carica.
che la carica scende esponenzialmente
mentre la corrente
parte dal
valore che avrebbe se non ci fosse il
condensatore,
cioè
εR
per
lim Q(t ) 0
lim i(t ) 0
a zero partendo dal valore massimo
εC ,
εC
t
Guardandone gli andamenti si vede
t
t
ε
t
R
annullarsi. Anche in questo caso il tempo teorico di
annullamento sarebbe infinito, ma nella pratica dopo t 4
non c’è più corrente.
R
12. L’area sottesa dalla curva
i(t ) si può esprimere per
mezzo della somma delle aree dei rettangoli di base t ed
altezza
i(5 s)
i(t ) . Ogni rettangolo ha per area il piccolo
incremento di carica Q dato che:
i(t )
ε
Q
t
Q t i(t ) base altezza
i(10 s)
i(3 )
L’area totale eguaglia dunque la carica Q complessivamente
5 s 10 s
…
3
4
5
accumulata sul condensatore:
Q t1 i(t1 ) t2 i(t2 ) ...
che come sappiamo vale
εC .
La formula rigorosa si esprime
tramite il calcolo integrale nel modo che segue:
Q
i(t)dt εC
0
Osserviamo che:
1.
R
ε
R
C
All’inizio del processo di carica il condensatore si
comporta come un tratto di corto circuito (un pezzo di
filo ideale con R 0 ), poi man mano ostacola sempre più la
corrente. Ad esempio nel circuito a destra è come se la batteria
13
fosse collegata a due resistenze in parallelo, Req
si ha I
2.
ε
R
ε
RR
R
e
RR
2
2
R
2
Al termine del processo di carica il condensatore agisce come un
interruttore aperto ( R ). Nel circuito a fianco è come se il
tratto con il condensatore fosse aperto e si ha quindi I
3.
ε
R
Nel processo di scarica il condensatore svolge il ruolo di
generatore e la resistenza di scarica non è detto che sia la stessa
della carica, anzi, spesso si ha interesse a cambiarla per alterare i
tempi.
4.
Il circuito
è l’analogo elettrico dello sciacquone del
RC
gabinetto: accumula carica per poi rilasciarla tutta insieme (un
flusso di acqua costante non avrebbe lo stesso effetto dello
sciacquone).
i(t )
piccolo:
t
scarica veloce
grande:
come una batteria (TV, PC)
ε
R
A che serve un condensatore?
1.
Separa due porzioni di un circuito a potenziale differente.
2.
Produce scariche brevi ed intense come nel caso della macchina
defibrillatrice (una pila sul cuore non sarebbe lo stesso!) oppure
dei flash fotografici (c’è anche un t di carica)
3.
E’ usato nei circuiti
che producono fenomeni intervallati nel
tempo. Ad esempio il temporizzatore del tergicristallo può avere
maggiore o minore ritardo quando con la manopola alteriamo la
costante di tempo di un circuito
RC ,
e questo impiega un
tempo differente a caricarsi. Lo stesso principio per le frecce nelle
auto o per i pacemakers nel cuore.
4.
E’ usato come batteria in circuiti RC con costanti di tempo
molto grandi. In questo caso produce una corrente praticamente
costante per lunghissimo tempo. Ne sono esempi gli orologi del
PC oppure le memorie della TV, alimentate da n condensatore
caricato
quando è accesa. E’ infatti pericoloso aprire questi
14
apparecchi se non si è esperti: toccando un condensatore
potremmo farlo scaricare attraverso il nostro corpo producendo
una corrente anche molto grande.
Esempio Walker p.104 n. 16
Un circuito è formato da due resistenze ( 126 , 275 ) ed un
condensatore da 182 µF ed una batteria
ε 3.00 V
in serie.
Calcola: la costante di tempo, il valore massimo della carica sul
condensatore, dopo quanti secondi dalla chiusura dell’interruttore
ε
la carica avrà raggiunto l’ 80% del suo valore massimo.
Il valore massimo della carica è:
C
Qmax C 3.00V 182 10 F 546 10
ε
6
6
C
la costante di tempo vale:
ReqC (126 275) 182 106 F 73.0 103 s
Imponiamo che Q(t ) εC (1 e
t RC
) sia pari all’ 80% del suo valore
massimo, ottenendo:
εC (1 e t RC ) 0.80 εC
e
t RC
0.20
t RC ln 0.20 118 103 s
(Studiare pp 103-107. es p116 n 56, 57,58, 59)
4.4 Condensatori in serie e parallelo
Combinando fra loro condensatori differenti formando dei sistemi, si
potranno ottenere valori differenti di capacità, e quindi variare a
piacimento gli accumuli di energia potenziale.
1
SI
DICE CAPACITÀ EQUIVALENTE, DI UN SISTEMA DI CONDENSATORI, FRA
UN PUNTO
1
ED UN PUNTO
2,
LA CAPACITÀ DI QUEL CONDENSATORE CHE,
QUANDO VIENE COLLEGATA UNA SUA ARMATURA AL PUNTO
AL PUNTO
2, È IN
1
E L’ALTRA
GRADO DI ACCUMULARE LA STESSA ENERGIA POTENZIALE
A
DEL SISTEMA.
Vi sono, in realtà, solamente due modi diversi di mettere in relazione due
B
o più condensatori: in serie ed in parallelo.
Due (o più) condensatori si dicono collegati in serie fra un punto 1 ed
un punto 2 quando, per andare da 1 a 2 con un percorso continuo che
non inverta mai direzione, siamo costretti ad attraversare le armature di
tutti.
15
2
A e B in serie fra 1 e 2
La capacità equivalente di due condensatori A e B collegati in serie si
ricava tenendo conto del fatto che, posta una carica Q
sulla prima
armatura, essa si riprodurrà, per induzione, su tutte le altre con i segni
alternati, e che la differenza di potenziale fra il punto 1 ed il punto 2 è la
somma delle differenze di potenziale intermedie. Si scrive quindi:
V VA VB
La capacità equivalente C E , messa fra 1 e 2 al posto della serie, una
volta caricata con la medesima carica Q che si pone su ciascuno dei due
condensatori, dovrà generare una differenza di potenziale fra le sue
armature pari proprio a questo valore V . Solo in questo modo infatti
essa incamererà la stessa energia della serie. Dovrà quindi essere:
CE
E poiché è, per definizione, C A
Q
V
Q
Q
e CB
, sostituendo:
VA
VB
Q
Q
Q
CE
C A CB
e, semplificando:
1
1
1
1
CE
CA CB
Da tale formula si evince che la capacità equivalente ad una serie è più
piccola della più piccola capacità presente.
A
B
Due (o più) condensatori si dicono collegati in parallelo fra un punto 1 ed
un punto 2 se possiamo andare da 1 a 2, con un percorso continuo che
non inverta mai direzione, attraversando solo le due armature di uno
qualunque di essi.
La capacità equivalente di due condensatori posti in parallelo, si ricava
tenendo conto che la differenza di potenziale fra le armature di uno
qualunque di essi, è sempre pari alla differenza di potenziale V fra il
punto 1 ed il punto 2. Infatti
ognuno dei condensatori
ha la prima
armatura collegata con 1 e la seconda con 2: le armature di A e di B
collegate al punto 1 è come se fossero un unico conduttore, e lo stesso può
dirsi delle armature collegate al punto 2.
Pertanto, se le capacità sono differenti,
la carica su ognuna delle
armature di A sarà senz’altro differente da quella sulle armature di B, ma
16
2
A e B in parallelo fra 1 e 2
il prodotto di queste cariche
per ciascuna capacità deve sempre dare
V .
Questo è possibile solo se la carica totale Q QA QB , che poniamo
complessivamente sulle armature tramite un generatore, si ripartisce in
maniera proporzionale alle capacità:
QA CA V
QB CB V
Se ora, al posto del parallelo, si mette la capacità equivalente C E , tutta
la carica Q andrà sulle sue armature. Ma sappiamo che C E deve
incamerare la stessa energia del parallelo, e questo è possibile solo se
V resta lo stesso di prima, da cui:
CE
Q QB
Q
Q
Q
A
A B
V
V
V
V
A
B
Sostituendo abbiamo:
CE C A CB
Da questo risultato si deduce che la capacità di un parallelo è maggiore
della più grande capacità presente3.
La formula che addiziona le capacità in parallelo può essere intuita
osservando la figura accanto. Immaginiamo di allontanare le armature
connesse al punto 1 da quelle connesse al punto 2. Sarà allora più
trasparente che, ponendo in parallelo due condensatori, in realtà stiamo
accostando una sola armatura, composta da due lastre collegate fra loro,
ad una seconda armatura, composta sempre da due lastre collegate fra
loro. Appare quindi naturale sommare le capacità dei due se si vuole
sostituire al parallelo un solo oggetto.
Si provi, per esercizio, a
1
stabilire come sono disposti i
1
sistemi di
A
condensatori in figura.
A
C
B
B
D
3
Il motivo per cui la formula per la capacità in parallelo ricalca quella per la serie di
resistenze, e viceversa quella per la serie di condensatori ricorda il parallelo di resistenze è da
ricercarsi nel fatto che nella definizione di capacità la differenza di potenziale figura al
denominatore:
C Q
V
mentre nella definizione di resistenza che si ottiene dalla legge
di Ohm la differenza di potenziale figura al numeratore:
R V
I
.
2
2
Serie o parallelo fra 1 e 2 ?
17











