Capitolo 4
Soluzione degli esercizi
a cura di Rosa Falotico
Aggiornamenti a cura di Emanuela Furfaro
Esercizio 4.1
Variabile statistica X=Regione di provenienza, frequenze assolute e relative:
xi
Friuli
Lombardia
Piemonte
Veneto
fi
5
5
2
4
16
pi = fi /N
5/16=0.3125
5/16=0.3125
2/16=0.125
4/16=0.25
1
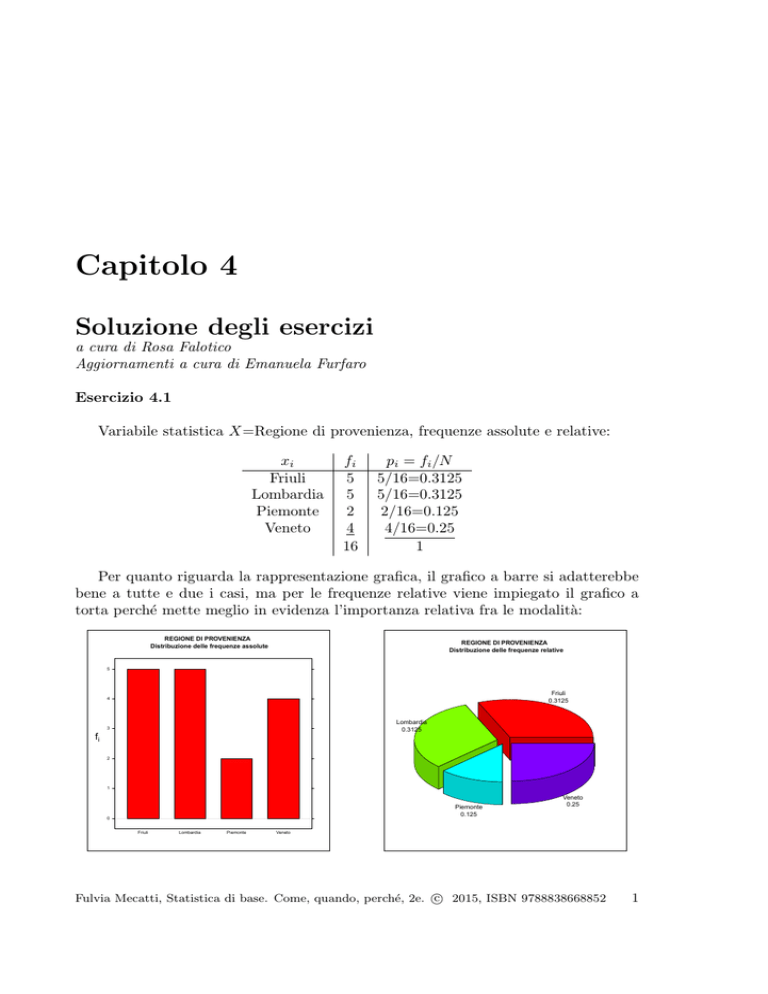
Per quanto riguarda la rappresentazione grafica, il grafico a barre si adatterebbe
bene a tutte e due i casi, ma per le frequenze relative viene impiegato il grafico a
torta perché mette meglio in evidenza l’importanza relativa fra le modalità:
REGIONE DI PROVENIENZA
Distribuzione delle frequenze assolute
REGIONE DI PROVENIENZA
Distribuzione delle frequenze relative
5
Friuli
0.3125
4
Lombardia
0.3125
3
fi
2
1
Piemonte
0.125
0
Friuli
Lombardia
Piemonte
Veneto
0.25
Veneto
c 2015, ISBN 9788838668852
Fulvia Mecatti, Statistica di base. Come, quando, perché, 2e. 1
2
Capitolo 4 - Soluzioni degli esercizi
Variabile statistica Y =titolo di studio del/della capofamiglia, frequenze assolute
e relative:
yi
Nessuno
Elementari
Medie
Diploma
Laurea
Post-laurea
fi
1
3
3
6
2
1
16
pi = fi /N
1/16=0.0625
3/16=0.1875
3/16=0.1875
6/16=0.375
2/16=0.125
1/16=0.0625
1
Per quanto riguarda la rappresentazione grafica, il grafico a barre si adatterebbe
bene a tutte e due i casi, ma per le frequenze relative viene impiegato il grafico a
torta perché mette meglio in evidenza l’importanza relativa fra le modalità:
TITOLO DI STUDIO CAPOFAMIGLIA
Distribuzione delle frequenze assolute
TITOLO DI STUDIO CAPOFAMIGLIA
Distribuzione delle frequenze relative
6
Medie
0.1875
5
Elementari
0.1875
4
fi
Nessuno
0.0625
3
2
Post−laurea
0.0625
1
Diploma
0.375
Laurea
0.125
0
Nessuno
Elementari
Medie
Diploma
Laurea
Post−laurea
Variabile statistica Z=Immobili di proprietà, frequenze assolute e relative:
zi
0
1
2
3
fi
7
5
3
1
16
pi = fi /N
7/16=0.4375
5/16=0.3125
3/16=0.1875
1/16=0.0625
1
c 2015, ISBN 9788838668852
Fulvia Mecatti, Statistica di base. Come, quando, perché, 2e. Capitolo 4 - Soluzioni degli esercizi
3
Rappresentazione grafica:
NUMERO IMMOBILI
Distribuzione delle frequenze assolute
NUMERO IMMOBILI
Distribuzione delle frequenze relative
7
0.6
6
0.5
5
0.4
4
pi 0.3
fi
3
0.2
2
0.1
1
0
0.0
0
1
2
3
0
1
2
3
Esercizio 4.2
Variabile statistica X =Numero ciliegie:
xi : xl ` xL
fi
0 ` 20
20 ` 40
40 ` 60
6
10
14
30
fi
∗ 100
N
20%
33.33%
46.67%
100%
%i =
ϕi
%i
%=
N
xL − xl
1.00
1.67
2.33
xL − xl
20
20
20
Rappresentazione grafica:
NUMERO CILIeGIE
Distribuzione delle frequenze percentuali
2.33
1.67
ϕi N%
1
0
0
20
40
60
c 2015, ISBN 9788838668852
Fulvia Mecatti, Statistica di base. Come, quando, perché, 2e. 4
Capitolo 4 - Soluzioni degli esercizi
Esercizio 4.3
Variabile statistica X =Litri di succo di frutta consumati mediamente in una
settimana:
xi : xl ` xL
fi
pi
Fi
Φi
xL − xl
0`2
2`4
4`6
6`8
2
5
10
3
20
0.1
0.25
0.5
0.15
1
2
7
17
20
0.10
0.35
0.85
1
2
2
2
2
ϕi =
fi
xL − xl
1
2.5
5
1.5
ϕi
pi
=
N
xL − xl
0.05
0.12
0.25
0.07
Rappresentazione grafica:
LITRI DI SUCCO DI FRUTTA SETTIMANALI
Distribuzione delle frequenze relative
0.25
0.85
0.20
0.15
φi
0.35
0.10
1
0.05
0.1
0.00
0
2
4
6
8
Dopo aver riportato sul grafico le frequenze relative cumulate se ne può dare
un’interpretazione notando che, a settimana, un decimo della popolazione di bimbi
beve non più di 2 litri di succo (area rossa) il 36% beve non più di 4 litri (area a riga
discendente) e l’85% (area a riga ascendente) beve non più di 6 litri di succo.
c 2015, ISBN 9788838668852
Fulvia Mecatti, Statistica di base. Come, quando, perché, 2e. Capitolo 4 - Soluzioni degli esercizi
5
Esercizio 4.4
Casteldeilonghi
xi : xl ` xL
fi
pi
Fi
Φi
xL − xl
1.7 ` 1.76
1.76 ` 1.82
1.82 ` 1.88
1.88 ` 1.94
1.94 ` 2.00
0
2
3
3
2
10
0.00
0.20
0.30
0.30
0.20
1
0
2
5
8
10
0.00
0.20
0.50
0.80
1.00
0.06
0.06
0.06
0.06
0.06
yi : yl ` yL
fi
pi
Fi
Φi
yL − yl
1.7 ` 1.76
1.76 ` 1.82
1.82 ` 1.88
1.88 ` 1.94
1.94 ` 2.00
3
3
1
3
2
12
0.25
0.25
0.08
0.25
0.17
1
3
6
7
10
12
0.25
0.50
0.58
0.83
1.00
0.06
0.06
0.06
0.06
0.06
fi
xL − xl
0.00
33.33
50.00
50.00
33.33
pi
ϕi
=
N
xL − xl
0.00
3.33
5.00
5.00
3.33
fi
yL − yl
50.00
50.00
16.67
50.00
33.33
ϕi
pi
=
N
yL − yl
4.17
4.17
1.39
4.17
2.78
ϕi =
Altecime
ϕi =
CASTELDEILONGHI:
Grafico delle frequenze relative
0.3
ALTECIME:
Grafico delle frequenze relative
0.3
5
5
0.25
4.17
0.2
3.33
0.17
2.78
ϕi N
ϕi N
0.8
0.5
0.08
1.39
0
0
1.70
1.76
1.82
1.88
1.94
2.00
1.70
1.76
1.82
1.88
1.94
2.00
Poiché le due popolazioni hanno una differente numerosità bisogna impiegare le
frequenze relative. Appare evidente dal confronto delle frequenze cumulate relative,
e ancor più dai grafici che i giovani di Casteldeilonghi sono più alti, infatti circa l’80%
è alto almeno 1.82m contro il 50% dei giovani di Altecime.
c 2015, ISBN 9788838668852
Fulvia Mecatti, Statistica di base. Come, quando, perché, 2e. 6
Capitolo 4 - Soluzioni degli esercizi
Esercizio 4.5
Variabile statistica X=numero di scarpe possedute, frequenze assolute e relative:
xi
fi
5
6
7
8
1
2
3
4
10
fi
N
1/10=0.1
2/10=0.2
3/10=0.3
4/10=0.4
1
pi =
Fi
Φi
1
3
6
10
0.10
0.30
0.60
1.00
La variabile è quantitativa discreta: ha senso costruire le frequenze cumulate.
Variabile statistica Y =colore dei capelli, frequenze assolute e percentuali:
yi
biondo
castano
rosso
fi
pi = N
∗ 100
50%
40%
10%
100%
fi
5
4
1
10
La variabile è qualitativa sconnessa: non ha senso costruire le frequenze cumulate.
Variabile statistica Z =misura del piede, frequenze assolute e relative:
zi
fi
35
36
37
38
39
40
1
2
2
3
1
1
10
fi
N
0.10
0.20
0.20
0.30
0.10
0.10
1
pi =
Fi
Φi
1
3
5
8
9
10
0.10
0.30
0.50
0.80
0.90
1.00
La variabile è quantitativa discreta: ha senso costruire le frequenze cumulate.
Variabile statistica K =titolo di studio, frequenze assolute e percentuali:
ki
medie
superiori
università
fi
2
5
3
10
pi %
20 %
50 %
30 %
100%
Fi
2
7
10
Φi %
20 %
70 %
100 %
La variabile è qualitativa ordinale: ha senso costruire le frequenze cumulate.
c 2015, ISBN 9788838668852
Fulvia Mecatti, Statistica di base. Come, quando, perché, 2e. Capitolo 4 - Soluzioni degli esercizi
7
Esercizio 4.6
Variabile statistica X = stipendio mensile:
xi : xl a xL
(1.2 a 1.3)
(1.3 a 1.4)
(1.4 a 1.5)
(1.5 a 1.6)
(1.6 a 1.7)
(1.7 a 1.8)
fi
7
4
5
4
2
2
24
pi
0.29
0.17
0.21
0.17
0.08
0.08
1
Fi
7
11
16
20
22
24
Φi
0.29
0.46
0.67
0.84
0.92
1.00
xL − xl
0.10
0.10
0.10
0.10
0.10
0.10
i
φi = xLf−x
l
70
40
50
40
20
20
φi
N
2.92
1.67
2.08
1.67
0.83
0.83
STIPENDIO MENSILE
Distribuzione delle frequenze relative
3.0
2.5
2.0
φi 1.5
0.29
1.0
0.5
0.0
1.2
1.3
1.4
1.5
1.6
1.7
1.8
Il 25% degli stipendi più bassi cade nel primo intervallo (1.200 a 1.300) che ne
contiene il 29%, quindi il massimo livello raggiungibile è 1.300 migliaia di euro.
c 2015, ISBN 9788838668852
Fulvia Mecatti, Statistica di base. Come, quando, perché, 2e. 8
Capitolo 4 - Soluzioni degli esercizi
Esercizio 4.7
Variabile statistica X = minuti impiegati per soluzione degli esercizi:
xi : xl a xL
(0 a 10)
(10 a 15)
(15 a 18)
fi
9
2
1
12
pi
0.75
0.17
0.08
1
Fi
9
11
12
Φi
0.75
0.92
1.00
xL − xl
10.00
5.00
3.00
i
φi = xLf−x
l
0.90
0.40
0.33
φi
N
0.075
0.034
0.028
STIPENDIO MENSILE
Distribuzione delle frequenze relative
0.075
φi
75%
0.034
0.027
17%
8%
0
0
10
15
18
Possiamo notare come la maggior parte degli esercizi (il 75%) richieda al massimo
10 minuti per la soluzione, solo il 25% degli esercizi richiede più di 10 minuti e solo
l’8% più di 15 minuti.
Essendo i dati raggruppati, usando il grafico possiamo determinare solo la percentuale degli estremi dei gruppi a cui le modalità richieste appartengono, quindi gli
esercizi che richiedono non meno di 12 minuti appartengono alla seconda e alla terza
classe, quindi rappresentano il 25% della popolazione(righe discendenti), mentre gli
esercizi che richiedono al massimo 13 minuti appartengono alla prima e alla seconda
classe e rappresentano il 92% della popolazione (righe ascendenti).
c 2015, ISBN 9788838668852
Fulvia Mecatti, Statistica di base. Come, quando, perché, 2e. Capitolo 4 - Soluzioni degli esercizi
9
Esercizio 4.8
Variabile statistica X = gusto delle caramelle vendute il 31 dicembre:
xi
Cioccolato
Fragola
Limone
Menta
fi
15
8
11
16
50
pi
0.30
0.16
0.22
0.32
1
Variabile statistica Y = gusto delle caramelle vendute il 30 giugno:
yi
Cioccolato
Fragola
Limone
Menta
fi
4
11
15
10
40
pi
0.10
0.28
0.38
0.25
1
VENDITA CARAMELLE
Grafico delle frequenze relative
0.5
31 dicembre
30 giugno
0.4
0.3
0.2
0.1
0.0
Cioccolato
Fragola
Limone
Menta
Appare evidente che il 31 gennaio non ci sia stato un gusto nettamente più richiesto, benché tendano a prevalere cioccolato e menta e la fragola non sia stata
particolarmente ricercata, mentre il 30 giugno il limone si è mostrato nettamente più
gradito, soprattutto a discapito del cioccolato che vede calare bruscamente le proprie
vendite.
c 2015, ISBN 9788838668852
Fulvia Mecatti, Statistica di base. Come, quando, perché, 2e. 10
Capitolo 4 - Soluzioni degli esercizi
Esercizio 4.9
Variabile statistica X = gradimento televisivo:
xi
molto noioso
noioso
interessante
molto interessante
fi
5
9
12
4
30
pi %
16.67%
30%
40%
13.33%
100%
Fi
5
14
26
30
Φi
16.67%
46.67%
86.67%
100%
GRADIMENTO TELEVISIVO
Grafico delle frequenze percentuali
50
26
86.67 %
40
30
20
10
5
16.67 %
9
30 %
12
40 %
molto noioso
noioso
interessante
0
molto interessante
Il numero di risposte non superiori ad interessante è 26 e la relativa percentuale
è 86.67%
c 2015, ISBN 9788838668852
Fulvia Mecatti, Statistica di base. Come, quando, perché, 2e. Capitolo 4 - Soluzioni degli esercizi
11
Esercizio 4.10
Variabile statistica X = età degli acquirenti:
xi
11
12
13
14
15
fi
11
9
8
21
1
50
pi
0.22
0.18
0.16
0.42
0.02
1
pi %
22 %
18 %
16 %
42 %
2%
100%
Fi
11
20
28
49
50
Φi
0.22
0.40
0.56
0.98
1.00
Φi %
22 %
40 %
56 %
98 %
100 %
ETA' ACQUIRENTI LIBRO
Grafico delle frequenze relative
0.5
Almeno 13 anni
56 %
0.4
0.3
Non più di 14 anni
60 %
0.2
0.1
0.0
11
12
13
14
15
La percentuale di acquirenti aventi almeno 13 anni è il 56%, mentri gli acquirenti
aventi non più di 14 anni sono il 60%.
c 2015, ISBN 9788838668852
Fulvia Mecatti, Statistica di base. Come, quando, perché, 2e. 12
Capitolo 4 - Soluzioni degli esercizi
Esercizio 4.11
Variabile statistica X =spesa in elettronica degli utenti base:
xi
(0 a 200)
(200 a 300)
(300 a 400)
(400 a 500)
(500 a 1000)
fi
4
16
17
8
5
50
pi
8%
32 %
34 %
16 %
10 %
100%
Fi
4
20
37
45
50
Φi
8%
40%
74%
90%
100%
xL − xl
200
100
100
100
500
i
φi = xLf−x
l
0.02
0.16
0.17
0.08
0.01
φi
N
0.04
0.32
0.34
0.16
0.02
Variabile statistica Y =spesa in elettronica degli utenti professionali:
yi
(0 a 200)
(200 a 300)
(300 a 400)
(400 a 500)
(500 a 1000)
fi
1
2
3
6
8
20
pi %
5%
10 %
15 %
30 %
40%
100 %
Fi
1
3
6
12
20
Φi %
5%
15%
30%
60%
100%
xL − xl
200
100
100
100
500.00
i
φi = xLf−x
l
0.00
0.02
0.03
0.06
0.02
φi
N
0.02
0.10
0.15
0.30
0.08
UTENTI INFORMATICI
Grafici delle frequenze percentuali
0.34
0.32
ϕi%/N
Base
Professionali
74 %
0.16
0.04
0.02
0
0.02
0.08
0.1
30 %
0.15
0.3
0
200
300
400
500
1000
Si può facilmente notare che la maggior parte (74%) dei clienti base effettua acquisti di minore per un valore non superiore ai 400 euro, mentre avviene il contrario
per i clienti professionali, che solo nel 30% dei casi effettua acquisti inferiori a tale
somma. Se ne deduce che i clienti professionali, benché siano in numero minore,
c 2015, ISBN 9788838668852
Fulvia Mecatti, Statistica di base. Come, quando, perché, 2e. Capitolo 4 - Soluzioni degli esercizi
13
effettuano acquisti più costosi.
Esercizio 4.12
1
V
2
F
3
F
4
V
5
V
6
V
7
V
8
F
9
F
10
V
Esercizio 4.13
Scegli la risposta (più) corretta
1. La definizione di frequenza relativa è:
• il rapporto fra frequenza assoluta e numerositpià della popolazione, in
fi
formule: pi = N
2. La definizione di frequenze cumulate (assolute) è:
• la somma delle frequenze
associate alle modalità inferiori nell’orPassolute
i
dinamento, in formule: j=1 fj
3. La somma delle frequenze relative è:
• 1
4. Il grafico più corretto per rappresentare la distribuzione di frequenza di un
fenomeno quantitativo continuo è:
• istogramma con gli intervalli sulle ascisse e le frequenze sulle ordinate
5. Il valore centrale di un intervallo è:
xL + xl
• x∗i =
2
c 2015, ISBN 9788838668852
Fulvia Mecatti, Statistica di base. Come, quando, perché, 2e.












