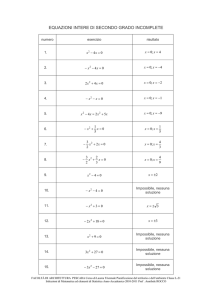
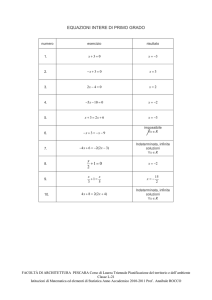
RISOLUZIONE ESERCIZI CALCOLO DEI LIMITI
•
Calcolare i seguenti limiti:
FORME DETERMINATE
1)
lim( x + 3) = 4 2) lim( x + 3) = 5 3) lim( − x + 3 log 2 x ) = −2 + 3 ⋅ 1 = 1 4) lim ( 2 x + 1) =
5)
lim( x + 3 x + 4 ) = 6 6) lim
x→4
x →1
10)
14)
x→2
x→0
x →1
(
)
(
2
)
1
1
1
= ∞ 7) lim+
= +∞ 8) lim
= 0 9) lim 2 x + 3x = 0 − ∞ = −∞
x
→
∞
x → −∞
x →1 x − 1
x −1
x −1
(
lim 2 + x = +∞ 11) lim 2
x → +∞
x
x → −1
1
3
+1=
2
2
x → −∞
−x
x
x +5
1
− x = +∞ 12) lim log x − = +∞ 13) lim
=3
x → +∞
x
→
1
x +1
2
)
2x
2− x
2
2
log x
= 0 16) lim x = +∞ 17) lim x = 0 18) lim+ x = −∞
= +∞ 15) lim
x → +∞ 5
x → +∞ 5
x → −∞ 5
x → +∞ 5
x→0
5
lim
FORME INDETERMINATE
FUNZIONI RAZIONALI INTERE
∞−∞
Per risolvere la forma indeterminata si raccoglie il termine di grado più elevato , in tal modo si elimina la forma
indeterminata. Praticamente il risultato del limite è dato dal valore assunto dal termine più alto in grado.
(
(
)
1
lim x 2 − x = lim x 2 ⋅ 1 − = +∞
x → +∞
x
2
3
20) lim − x + x = +∞
19)
x → +∞
x → +∞
)
(
(
)
)
1 1
5
lim 2 x 4 + x 3 − x 2 + 5 = lim x 4 ⋅ 2 + − 2 + 4 = +∞
x → +∞
x → +∞
x x
x
5
3
2
22) lim − x + x − x + 5 = +∞
21)
x → −∞
FUNZIONI RAZIONALI FRATTE
0
0
Per risolvere la forma indeterminata si scompongono entrambi i polinomi a numeratore e denominatore, si
semplificano le espressioni comuni; in tal modo si elimina la forma indeterminata. A volte è necessario procedere
a passaggi suppletivi per semplificare ulteriormente altre espressioni comuni e quindi il fattore di
indeterminazione.
Principali regole di scomposizione:
1. raccoglimento a fattore comune
2. quadrato di binomio
3. differenza di quadrati
4. trinomio di secondo grado
ax 2 + bx = x ⋅ (ax + b )
x 2 ± 2 x + 1 = ( x ± 1) ;
2
x 2 − y 2 = (x + y ) ⋅ (x − y ) ;
ax 2 + bx + c = a ⋅ ( x − x1 ) ⋅ ( x − x 2 ) con x1 , x 2 soluzione dell’equazione
FACOLTÀ DI ARCHITETTURA PESCARA Corso di Laurea Triennale Pianificazione del territorio e dell’ambiente Classe L-21
Istituzioni di Matematica ed elementi di Statistica Anno Accademico 2010-2011 Prof . Annibale ROCCO
ESERCIZI SUI LIMITI
Pagina 1 di 8
FACOLTÀ DI ARCHITETTURA PESCARA Corso di Laurea Triennale Pianificazione del territorio e dell’ambiente Classe L-21
Istituzioni di Matematica ed elementi di Statistica Anno Accademico 2010-2011 Prof . Annibale ROCCO
ESERCIZI SUI LIMITI
Pagina 2 di 8
FACOLTÀ DI ARCHITETTURA PESCARA Corso di Laurea Triennale Pianificazione del territorio e dell’ambiente Classe L-21
Istituzioni di Matematica ed elementi di Statistica Anno Accademico 2010-2011 Prof . Annibale ROCCO
ESERCIZI SUI LIMITI
Pagina 3 di 8
+∞
FACOLTÀ DI ARCHITETTURA PESCARA Corso di Laurea Triennale Pianificazione del territorio e dell’ambiente Classe L-21
Istituzioni di Matematica ed elementi di Statistica Anno Accademico 2010-2011 Prof . Annibale ROCCO
ESERCIZI SUI LIMITI
Pagina 4 di 8
FACOLTÀ DI ARCHITETTURA PESCARA Corso di Laurea Triennale Pianificazione del territorio e dell’ambiente Classe L-21
Istituzioni di Matematica ed elementi di Statistica Anno Accademico 2010-2011 Prof . Annibale ROCCO
ESERCIZI SUI LIMITI
Pagina 5 di 8
FACOLTÀ DI ARCHITETTURA PESCARA Corso di Laurea Triennale Pianificazione del territorio e dell’ambiente Classe L-21
Istituzioni di Matematica ed elementi di Statistica Anno Accademico 2010-2011 Prof . Annibale ROCCO
ESERCIZI SUI LIMITI
Pagina 6 di 8
FACOLTÀ DI ARCHITETTURA PESCARA Corso di Laurea Triennale Pianificazione del territorio e dell’ambiente Classe L-21
Istituzioni di Matematica ed elementi di Statistica Anno Accademico 2010-2011 Prof . Annibale ROCCO
ESERCIZI SUI LIMITI
Pagina 7 di 8
2a
a
2
FACOLTÀ DI ARCHITETTURA PESCARA Corso di Laurea Triennale Pianificazione del territorio e dell’ambiente Classe L-21
Istituzioni di Matematica ed elementi di Statistica Anno Accademico 2010-2011 Prof . Annibale ROCCO
ESERCIZI SUI LIMITI
Pagina 8 di 8