PROGRAMMAZIONE MATEMATICA
2010-2011 CLASSE 1D
prof. Giuseppe Giacomuzzi
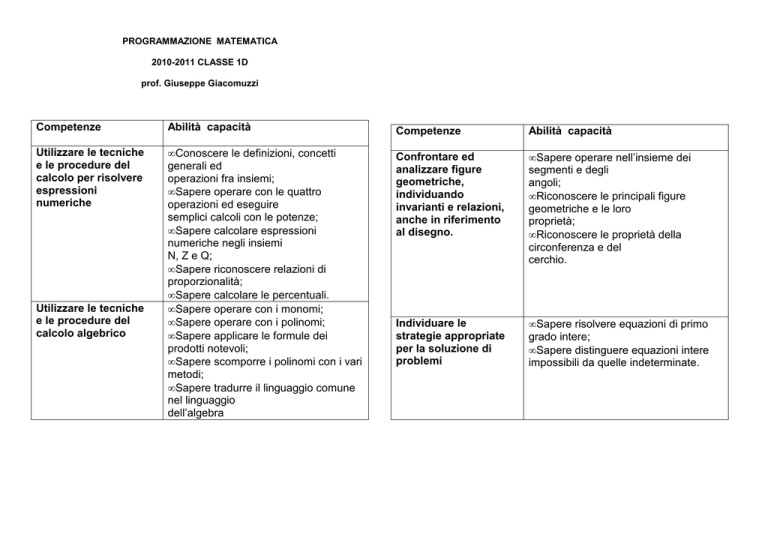
Competenze
Abilità capacità
Utilizzare le tecniche
e le procedure del
calcolo per risolvere
espressioni
numeriche
• Conoscere le definizioni, concetti
generali ed
operazioni fra insiemi;
• Sapere operare con le quattro
operazioni ed eseguire
semplici calcoli con le potenze;
• Sapere calcolare espressioni
numeriche negli insiemi
N, Z e Q;
• Sapere riconoscere relazioni di
proporzionalità;
• Sapere calcolare le percentuali.
• Sapere operare con i monomi;
• Sapere operare con i polinomi;
• Sapere applicare le formule dei
prodotti notevoli;
• Sapere scomporre i polinomi con i vari
metodi;
• Sapere tradurre il linguaggio comune
nel linguaggio
dell’algebra
Utilizzare le tecniche
e le procedure del
calcolo algebrico
Competenze
Abilità capacità
Confrontare ed
analizzare figure
geometriche,
individuando
invarianti e relazioni,
anche in riferimento
al disegno.
• Sapere operare nell’insieme dei
segmenti e degli
angoli;
• Riconoscere le principali figure
geometriche e le loro
proprietà;
• Riconoscere le proprietà della
circonferenza e del
cerchio.
Individuare le
strategie appropriate
per la soluzione di
problemi
• Sapere risolvere equazioni di primo
grado intere;
• Sapere distinguere equazioni intere
impossibili da quelle indeterminate.
MODULO N° 1 GLI INSIEMI NUMERICI
Esiti attesi
Sapere operare con le quattro operazioni e sapere eseguire semplici calcoli con
le potenze
Sapere calcolare espressioni numeriche negli insiemi N, Z e Q.
TEMPI DI ATTUAZIONE: ore 20
PREREQUISITI
• Conoscenza di base relative ai numeri.
TEMI/CONTENUTI
• Concetto di insieme e di sottoinsieme, operazioni con gli insiemi,
• Le quattro principali operazioni e le relazioni di confronto tra numeri naturali;
• L’elevamento a potenza e le proprietà delle potenze;
• Divisibilità e scomposizione di un numero in fattori primi, M.C.D. e m.c.m.;
• Espressioni numeriche;
• L’ampliamento dell’insieme N dei numeri naturali: i numeri interi relativi
(operazioni e loro proprietà);
• L’ampliamento dell’insieme Z dei numeri interi relativi: i numeri razionali
(operazioni e loro proprietà);
• Potenza ad esponente negativo;
• L’ampliamento dell’insieme Q dei numeri razionali: i numeri reali (operazioni e
loro proprietà).
STRATEGIE METODOLOGICHE SPECIFICHE DEL MODULO
Problem – solving, esercitazioni alla lavagna guidate, formazioni di gruppi di
lavoro, comunicazione nella forma verbale (lezione excattedra, conversazione).
PERCORSI DI ESPERIENZA
Utilizzo del laboratorio di informatica con uso di software (foglio elettronico,
software disciplinari, etc.).
FORME E TEMPI DI VERIFICA NON FISCALE
Esercitazioni alla lavagna e lavori di gruppo
FORME E TEMPI DI VERIFICA INTERMEDIA E FINALE DEL MODULO
Accertamenti orali e verifica scritta.
RECUPERO UNITA’ DI APPRENDIMENTO
ORE 5
==========================================================
MODULO N° 2 LE PROPORZIONI
Esiti attesi
Saper riconoscere funzioni di proporzionalità
Sapere calcolare le percentuali
TEMPI DI ATTUAZIONE: ore 5
PREREQUISITI
• Conoscenza delle operazioni con i numeri.
TEMI/CONTENUTI
• Il concetto di rapporto e sue applicazioni;
• Le proporzioni e le loro proprietà;
• Le percentuali.
STRATEGIE METODOLOGICHE SPECIFICHE DEL MODULO
Problem – solving, esercitazioni alla lavagna guidate, formazioni di gruppi di
lavoro, comunicazione nella forma verbale (lezione excattedra , conversazione).
PERCORSI DI ESPERIENZA
Utilizzo del laboratorio di informatica con uso di software (foglio elettronico,
software disciplinari, etc.).
FORME E TEMPI DI VERIFICA NON FISCALE
Esercitazioni alla lavagna e lavori di gruppo
FORME E TEMPI DI VERIFICA INTERMEDIA E FINALE DEL MODULO
Accertamenti orali
RECUPERO DEL MODULO
Nessuno
==========================================================
MODULO N° 3 I MONOMI
Esiti attesi
Sapere operare con i monomi
Sapere tradurre il linguaggio comune nel linguaggio dell’algebra
PREREQUISITI
• Conoscenza degli insiemi numerici;
• Conoscenza delle proprietà delle operazioni;
• Conoscenza delle proprietà delle potenze;
• Conoscenza dei monomi (operazioni e proprietà).
TEMPI DI ATTUAZIONE: ore 15
PREREQUISITI
• Conoscenza degli insiemi numerici;
• Conoscenza delle proprietà delle operazioni;
• Conoscenza delle proprietà delle potenze.
TEMI/CONTENUTI
• I polinomi: Addizioni e sottrazione tra polinomi;
• Prodotto di polinomi;
• Prodotti notevoli;
• Divisioni di polinomi;
• Teorema del resto e regola di Ruffini.
TEMI/CONTENUTI
• Monomi ed operazioni con i monomi;
• M.C.D. e m.c.m. tra monomi.
STRATEGIE METODOLOGICHE SPECIFICHE DEL MODULO
Problem – solving, esercitazioni alla lavagna guidate, formazioni di gruppi di
lavoro, comunicazione nella forma verbale (lezione excattedra , conversazione).
STRATEGIE METODOLOGICHE SPECIFICHE DEL MODULO
Problem – solving, esercitazioni alla lavagna guidate, formazioni di gruppi di
lavoro, comunicazione nella forma verbale (lezione excattedra , conversazione).
PERCORSI DI ESPERIENZA
Utilizzo del laboratorio di informatica con uso di software (foglio elettronico,
software disciplinari, etc.).
PERCORSI DI ESPERIENZA Utilizzo del laboratorio di informatica con uso di
software (foglio elettronico, software disciplinari, etc.).
FORME E TEMPI DI VERIFICA NON FISCALE
Esercitazioni e lavori di gruppo
FORME E TEMPI DI VERIFICA NON FISCALE
Esercitazioni in laboratorio
FORME E TEMPI DI VERIFICA INTERMEDIA E FINALE DEL MODULO
Verifiche orali e scritte
FORME E TEMPI DI VERIFICA INTERMEDIA E FINALE DEL MODULO
Esercitazioni alla lavagna, colloqui e lavori di gruppo
RECUPERO DEL MODULO
ORE 4
==========================================================
RECUPERO DEL MODULO
ORE 2
==========================================================
MODULO N° 4 I POLINOMI
Esiti attesi
Sapere operare con i polinomi
Sapere applicare le formule dei prodotti notevoli
Sapere tradurre il linguaggio comune nel linguaggio dell’algebra
TEMPI DI ATTUAZIONE: ore 20
MODULO N° 5 LE SCOMPOSIZIONI DI POLINOMI
Esiti attesi
Sapere scomporre i polinomi con i vari metodi;
Sapere tradurre il linguaggio comune nel linguaggio dell’algebra.
TEMPI DI ATTUAZIONE: ore 15
PREREQUISITI
• Conoscenza dei monomi (operazioni e proprietà).
• Conoscenza dei polinomi (operazioni e proprietà);
• Conoscenza dei prodotti notevoli;
• Conoscenza della Regola di Ruffini.
TEMI/CONTENUTI
• La scomposizione dei polinomi;
• Raccoglimento parziale e totale;
• Scomposizione mediante i prodotti notevoli;
• Il trinomio caratteristico;
• Scomposizione mediante il teorema di Ruffini e la divisione tra polinomi.
PERCORSI DI ESPERIENZA
Utilizzo del laboratorio di informatica con uso di software (foglio elettronico,
software disciplinari, etc.).
STRATEGIE METODOLOGICHE SPECIFICHE DEL MODULO
Problem – solving. Braing – Storming. Esercitazioni alla lavagna guidate,
formazioni di gruppi di lavoro, comunicazione nella forma verbale (lezione
excattedra , conversazione).
FORME E TEMPI DI VERIFICA INTERMEDIA E FINALE DEL MODULO
Accertamenti orali
FORME E TEMPI DI VERIFICA NON FISCALE
Esercitazioni alla lavagna e lavori di gruppo
RECUPERO DEL MODULO
ORE 1
PERCORSI DI ESPERIENZA
Laboratorio d’informatica
==========================================================
FORME E TEMPI DI VERIFICA NON FISCALE
Esercitazioni e lavori di gruppo
MODULO N° 7 I POLIGONI ED IN PARTICOLARE IL TRIANGO LO
Esiti attesi
Riconoscere le principali figure geometriche e le loro proprietà
FORME E TEMPI DI VERIFICA INTERMEDIA E FINALE DEL MODULO
RECUPERO DEL MODULO
ORE 4
==========================================================
MODULO N° 6 CONCETTI GEOMETRICI FONDAMENTALI
Esiti attesi
Sapere operare nell’insieme dei segmenti e degli angoli
TEMPI DI ATTUAZIONE (in ore) 5
PREREQUISITI
• Avere la percezione dello spazio.
TEMI/CONTENUTI
• Significato e caratteristiche degli assiomi;
• Gli enti geometrici primitivi;
• Confronto e somma di segmenti;
• Confronto e somma di angoli convessi.
STRATEGIE METODOLOGICHE SPECIFICHE DEL MODULO
Problem – solving, esercitazioni alla lavagna guidate, formazioni di gruppi di
lavoro, comunicazione nella forma verbale (lezione excattedra , conversazione).
TEMPI DI ATTUAZIONE: ore 8
PREREQUISITI
• Avere la percezione dello spazio.
TEMI/CONTENUTI
• I poligoni,
• Il concetto di teorema;
• Il triangolo e i criteri di uguaglianza;
• Il triangolo isoscele e le sue proprietà;
• La classificazione dei triangoli.
STRATEGIE METODOLOGICHE SPECIFICHE DEL MODULO
Problem – solving, esercitazioni alla lavagna guidate, formazioni di gruppi di
lavoro, comunicazione nella forma verbale (lezione excattedra , conversazione).
PERCORSI DI ESPERIENZA
Utilizzo del laboratorio di informatica con uso di software (foglio elettronico,
software disciplinari, etc.).
FORME E TEMPI DI VERIFICA NON FISCALE
Esercitazioni alla lavagna e lavori di gruppo
FORME E TEMPI DI VERIFICA INTERMEDIA E FINALE DEL MODULO
Accertamenti orali
RECUPERO DEL MODULO
ORE 2
PREREQUISITI
• Avere la percezione dello spazio.
==========================================================
TEMI/CONTENUTI
• Circonferenza
• Cerchio.
MODULO N° 8 QUADRILATERI PARTICOLARI
Esiti attesi
Riconoscere le principali figure geometriche e le loro proprietà.
STRATEGIE METODOLOGICHE DEL MODULO
Problem – solving, esercitazioni alla lavagna guidate, formazioni di gruppi di
lavoro, comunicazione e nella forma verbale (lezione excattedra, conversazione).
TEMPI DI ATTUAZIONE: ore 5
PERCORSI DI ESPERIENZA
Utilizzo del laboratorio di informatica con uso di software (foglio elettronico,
software disciplinari, etc.).
TEMI/CONTENUTI
• Il trapezio
• Il parallelogramma
• Il rettangolo, il rombo ed il quadrato.
PREREQUISITI
• Avere la percezione dello spazio.
STRATEGIE METODOLOGICHE DEL MODULO
Problem – solving, esercitazioni alla lavagna guidate, formazioni di gruppi di
lavoro, comunicazioni e nella forma verbale (lezione excattedra, conversazione).
PERCORSI DI ESPERIENZA
Utilizzo del laboratorio di informatica con uso di software (foglio elettronico,
software disciplinari, etc.).
FORME E TEMPI DI VERIFICA NON FISCALE
Esercitazioni in classe.
FORME E TEMPI DI VERIFICA INTERMEDIA E FINALE DEL MODULO
Accertamenti orali.
RECUPERO DEL MODULO
ORE 1
==========================================================
MODULO N° 9 CIRCONFERENZA E CERCHIO
Esiti attesi
Riconoscere le proprietà della circonferenza e del cerchio.
TEMPI DI ATTUAZIONE: ore 5
FORME E TEMPI DI VERIFICA NON FISCALE
Esercitazioni in classe.
FORME E TEMPI DI VERIFICA INTERMEDIA E FINALE DEL MODULO
Accertamenti orali e Verifica scritta.
RECUPERO UNITA’ DI APPRENDIMENTO
Nessuno
==========================================================