Indici di posizione - UniFI

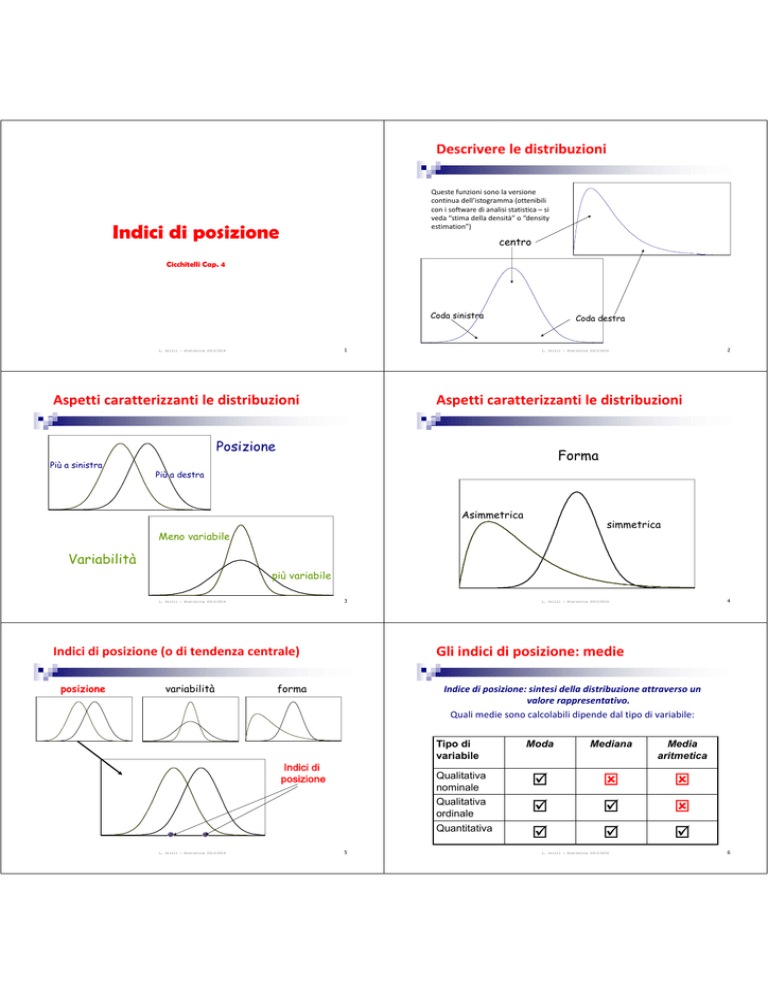
Descrivere le distribuzioni
Queste funzioni sono la versione continua dell’istogramma (ottenibili con i software di analisi statistica – si veda “stima della densità” o “density
estimation”)
Indici di posizione
centro
Cicchitelli Cap. 4
Coda sinistra
1
L. Grilli - Statistica 2013/2014
Aspetti caratterizzanti le distribuzioni
Coda destra
Aspetti caratterizzanti le distribuzioni
Posizione
Più a sinistra
2
L. Grilli - Statistica 2013/2014
Forma
Più a destra
Asimmetrica
simmetrica
Meno variabile
Variabilità
più variabile
3
L. Grilli - Statistica 2013/2014
Gli indici di posizione: medie
Indici di posizione (o di tendenza centrale)
posizione
variabilità
forma
Indice di posizione: sintesi della distribuzione attraverso un valore rappresentativo. Quali medie sono calcolabili dipende dal tipo di variabile:
Tipo di
variabile
Indici di
posizione
L. Grilli - Statistica 2013/2014
4
L. Grilli - Statistica 2013/2014
Qualitativa
nominale
Qualitativa
ordinale
Quantitativa
5
Moda
Mediana
Media
aritmetica









L. Grilli - Statistica 2013/2014
6
Media aritmetica
Un indice di posizione è solo una sintesi
X v.s. quantitativa
centro
0
25
{x1,x2,…,xN} successione
centro
50
75
100
0
25
50
dispersione
75
stesso centro, dispersione diversa
1
M 
N
100
dispersione
esempio
N
x
i 1
i
X: 2 3 2 6  M = (2+3+2+6)/4 = 3.25
Se il carattere è discreto la media, in generale, non appartenere
all’insieme delle modalità (es. numero medio di figli)
MEDIA: CENTRO DELL’INSIEME DEGLI N PUNTI
Se la distribuzione
è bimodale il
centro non è una
buona sintesi della
distribuzione!
x1
0
25
50
75
7
Proprietà della media aritmetica

Internalità (propr. di Cauchy)

Baricentro
N

xmin  M  xmax

 x k
i 1
N
NM   xi

i 1

N
2

 D(k ) è minimo quando k  M

r
i 1
Cr
Centro di ordine 2 (minimi quadrati) N
r
i
Cr : arg min  xi  Cr
Proprietà delle trasformazioni lineari
D(k )    xi  k 
8
Il centro di ordine r dell’insieme di punti {x1,x2,…,xN} è il valore che rende minima la distanza di ordine r
Y = a + bX  M Y = a + bM X

XN
Distanza di ordine r tra l’insieme di punti {x1,x2,…,xN} e il
punto k
N
( xi  M )  0
Lascia invariato l’ammontare complessivo:
XN-1
L. Grilli - Statistica 2013/2014
Media come ‘centro’
i 1

M
x2
100
L. Grilli - Statistica 2013/2014
Per r =2  C2 = M media aritmetica
Per r =1  C1 = Me mediana
i 1
9
L. Grilli - Statistica 2013/2014
Media aritmetica (distribuzione di frequenze)
10
L. Grilli - Statistica 2013/2014
Due modi di calcolare la media
Distribuzione di frequenze: (xj, nj) j=1,2,…,k
Tabella di frequenza
Mod.tà
Freq.
x1
n1
f1
x2
n2
f2
…
…
…
xj
nj
fj
…
…
…
xk
nk
fk
N
1
Totale
Distribuzione di frequenze
Distribuzione disaggregata
Fr.rel.
39 29 43 52 39 44
40 31 44 35
M
1
N
k
L. Grilli - Statistica 2013/2014
1
k
x n x
j 1
29 31 35 39 40 43 44 52
j
j
j 1
j
fj
M
11
39  29  43  
 39.6
10
M
1
1
2
1
1
2
1
29 1  311  35 1  39  2  
 39.6
10
M  29 
1
1
1
2
 31  35   39     39.6
10
10
10
10
L. Grilli - Statistica 2013/2014
12
Media aritmetica (dati raggruppati)
Media ponderata
Seriazione: ((xj-1; xj), nj) j=1,2,…,k
Tabella di frequenza
Mod.tà
Freq.
Fr.rel.
x0-x1
n1
f1
x1-x2
n2
f2
…
…
…
xj-1-xj
nj
fj
…
…
…
xk-1-xk
nk
fk
N
1
Totale

La media pesata (o ponderata) è n
Ipotesi istogramma: equi‐distribuzione delle frequenze all’interno delle classi
Mw 

cj= (xj+ xj-1 )/2
k
k
c n  c
j 1
j
j
j 1
n
 w 
   i  xi
i 1  wTOT 
i i
i 1
wTOT
n
dove wTOT   wi
i 1
wi è il peso assegnato alla i‐ma osservazione
Valore centrale di classe:
1
M
N
w x

j
fj
Il peso w può essere la frequenza (dati in forma di tabella di frequenza) oppure il peso w può indicare l’importanza del valore (es. media del voto degli esami pesata con i crediti)
Gli indici dei prezzi sono speciali medie ponderate, in cui x è il prezzo del bene e w è la quantità scambiata
13
L. Grilli - Statistica 2013/2014
14
L. Grilli - Statistica 2013/2014
La moda
Moda e massimi locali
Moda: modalità cui corrisponde la frequenza più alta
La moda può essere fuorviante se la
distribuzione ha massimi locali
Frequenza modale = 37
Alberghi di Assisi per categoria
40
35
30
25
freq 20
15
10
5
0
1 stella
2 stelle
3 stelle
4 stelle
categoria
Attenzione: Nei dati raggruppati  la moda è la classe cui corrisponde la densità più alta (può essere diversa dalla classe con la frequenza più alta nel caso di classi con ampiezza variabile)
0
1
2
3
4
5
6
7
8
0
2
4
6
8
10
12
Moda = ‘2 stelle’
L. Grilli - Statistica 2013/2014
15
L. Grilli - Statistica 2013/2014
16