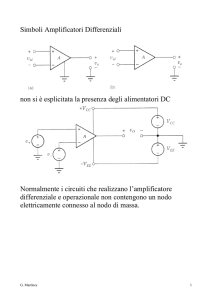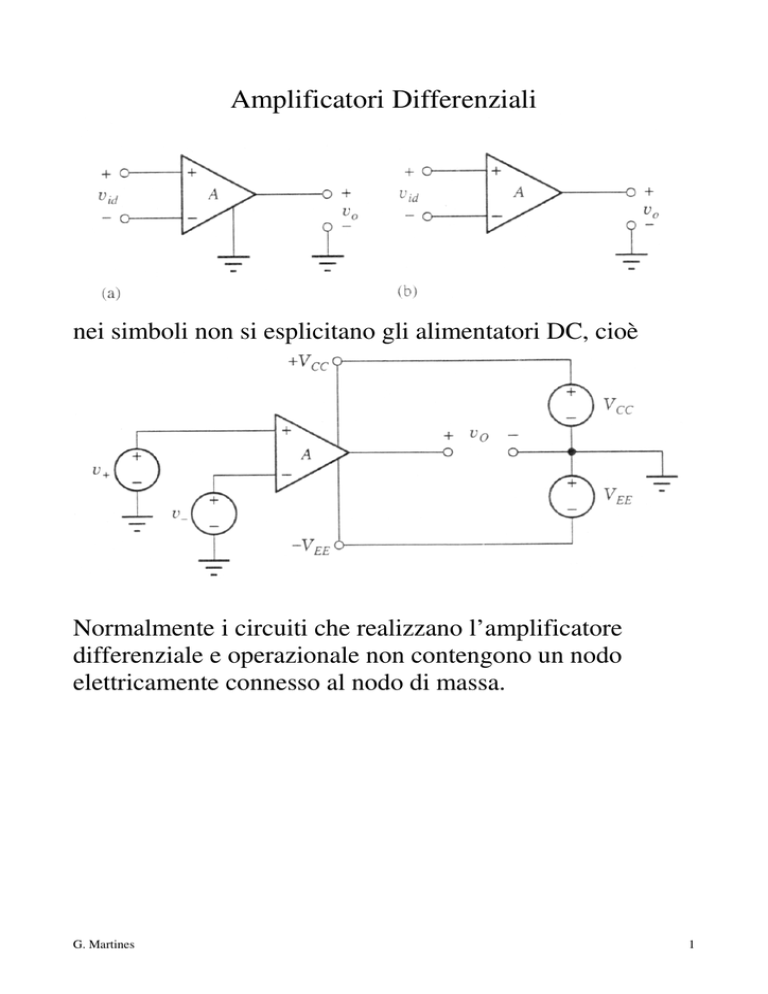
Amplificatori Differenziali
nei simboli non si esplicitano gli alimentatori DC, cioè
Normalmente i circuiti che realizzano l’amplificatore
differenziale e operazionale non contengono un nodo
elettricamente connesso al nodo di massa.
G. Martines
1
Amplificatore differenziale ideale
G. Martines
2
Amplificatore differenziale reale
Guadagno di tensione di un amplificatore differenziale
reale
L’Amplificatore operazionale è un amplificatore
differenziale con guadagno di tensione molto elevato.
G. Martines
3
Concetto di cortocircuito virtuale
Nella ipotesi che la tensione di uscita vo sia finita:
mentre le correnti di ingresso sono nulle nella ipotesi
RID = ∞
NOTA: la presenza della controreazione garantisce che la
tensione di uscita sia finita; basta considerare che il
guadagno ad anello chiuso può essere espresso da:
Af =
G. Martines
vo
A
A
1
=
≈
=
v s 1 + Aβ Aβ β
4
Ipotesi fondamentali per gli Amplificatori Operazionali ideali:
Altre proprietà degli Amplificatori Operazionali ideali:
G. Martines
5
Amplificatore Operazionale in configurazione
invertente
G. Martines
6
Con il concetto di cortocircuito virtuale:
Calcolo resistenza di uscita
G. Martines
7
Amplificatore Operazionale in configurazione
non-invertente
G. Martines
8
Analisi della configurazione non-invertente
G. Martines
9
Modello equivalente configurazione non-invertente
G. Martines
10
AMPLIFICATORE OPERAZIONALE REALE
Identificazione dello stadio amplificatore
G. Martines
11
GUADAGNO AD ANELLO APERTO FINITO
Consideriamo uno stadio non invertente:
G. Martines
12
Errore sul cortocircuito virtuale:
Errore sul guadagno ad anello chiuso (Gain Error):
ed in termini percentuali (Fractional Gain Error):
G. Martines
13
RESISTENZA DI USCITA NON NULLA
G. Martines
14
RESISTENZA DI INGRESSO FINITA
Configurazione non invertente:
G. Martines
15
RESISTENZA DI INGRESSO FINITA
Configurazione invertente:
G. Martines
16
RESISTENZA DI INGRESSO FINITA
Configurazione invertente:
G. Martines
17
G. Martines
18
RAPPORTO DI REIEZIONE DI MODO COMUNE FINITO
G. Martines
19
INSEGUITORE DI TENSIONE E CMRR
Gain Error:
G. Martines
20
RESISTENZA DI INGRESSO DI MODO COMUNE
G. Martines
21
TENSIONE DI OFFSET ALL’INGRESSO
G. Martines
22
CORRENTE DI POLARIZZAZIONE E OFFSET DI
CORRENTE ALL’INGRESSO
I B = (I B 2 + I B1 ) 2
G. Martines
23
COMPENSAZIONE DELLA CORRENTE DI
POLARIZZAZIONE
VOT = R2 I B 2 − I B1
G. Martines
24
COMPENSAZIONE DELLA CORRENTE DI
POLARIZZAZIONE IN AMPLIFICATORI AC
NOTA: La presenza della R3, se necessaria, riduce la
resistenza di ingresso nella configurazione non invertente
G. Martines
25
LIMITAZIONE DELLA CORRENTE DI USCITA
• La corrente di uscita di un amplificatore deve essere limitata
per evitare una eccessiva dissipazione di potenza nei circuiti
(sovraccarico)
• La limitazione su Io impone vincoli sulla RL ma anche sulla
rete di reazione.
G. Martines
26
RISPOSTA IN FREQUENZA
Gli operazionali si progettano in modo da avere elevato guadagno
DC e risposta in frequenza a singolo polo:
A0ωB è il prodotto guadagno-larghezza di banda GBW (A0
guadagno in continua, ωB banda a 3 dB)
ωT è la frequenza angolare di guadagno unitario (o di transizione)
per ω >> ωB: A(s ) =
G. Martines
A0ω
s
27
RISPOSTA IN FREQUENZA NON INVERTENTE
G. Martines
28
NOTA:
Aβ =
A
1
ovvero in dB
Aβ
dB
= A dB −
1
β
dB
β
per ω < ωH
|Aβ| > 1
e
Av(jω) = 1/β
per ω > ωH
|Aβ| < 1
e
Av(jω) = ωT/ω
per ω = ωH
|Aβ| = 1
G. Martines
29
RISPOSTA IN FREQUENZA INVERTENTE
In questo caso la reazione è parallelo-parallelo e quindi il
guadagno è la transresistenza, ma in termini di guadagno di
tensione si può scrivere in modo analogo al caso non
invertente:
NOTA:
G. Martines
AV(0) = 1 – 1/β
30
G. Martines
31
SLEW RATE
È una caratteristica del funzionamento a largo segnale degli
amplificatori operazionali
Modello equivalente di un amplificatore operazionale
G. Martines
32
Modello equivalente
di un amplificatore operazionale reale
dv O
SR =
dt
G. Martines
max
I max
=
C
33
LARGHEZZA DI BANDA A PIENA POTENZA
d (Vi sin ω t)
= ωVi cos ω t
dt
SR
fM =
2 πVO max
Per sinusoidi di ampiezza minore di VOmax vale ancora la relazione:
VO = VO max f M f .
G. Martines
34
SOMMATORE PESATO
G. Martines
35
AMPLIFICATORE DIFFERENZIALE
v+ =
R4
v2
R3 + R4
vO =
G. Martines
vO = v+ − IR2
I=
v1 − v+
R1
1 + R2 R1
R
v2 − 2 v1
1 + R3 R4
R1
36
AMPLIFICATORE DIFFERENZIALE
1 + R2 R1 − R2 R1 − R2 R3 R1 R4
vCM = 0
per v1 = v2 = vCM :
1 + R3 R4
R2
(v2 − v1 )
che si ha per R2/R1 = R4/R3
ed allora: vO =
R1
vO =
Resistenza di ingresso differenziale
RID = 2R1
G. Martines
37
Resistenze di ingresso dell'amplificatore differenziale
Svantaggio: RIN1 = R1
è diversa da
RIN2 = R1 + R2
i generatori vedono resistenze diverse (i1 ≠ i3)
non si ottiene facilmente un guadagno variabile
G. Martines
38
AMPLIFICATORE DIFFERENZIALE PER
STRUMENTAZIONE
G. Martines
39
CONVERTITORE CORRENTE-TENSIONE
VO = − I S R2
la configurazione invertente con generatore di segnale nella
forma di Norton.
AMPLIFICATORE PARAFASE
Av = 2
ma l’uscita non ha punti a massa
Convertitore di segno: Av = -1
(configurazione invertente con R2 = R1)
G. Martines
40
INVERTENTE AD ALTA RESISTENZA
G. Martines
41
RETE DI REAZIONE REATTIVA
Considerazioni valide per tutte configurazioni viste.
G. Martines
42
SFASATORE
Invertente: se Z 1 (s ) = Z 2 (s )
la differenza di fase fra
segnale di uscita e di ingresso vale:
π + ∠Z 2 (s ) − ∠Z1 (s )
differenziatore: (più facile la sintesi)
Vo
1
1
= s −
s +
Vi CR
CR
G. Martines
Φ = π − 2 tan −1 (ωCR )
43
AMPLIFICATORE PASSA-BASSO
G. Martines
44
AMPLIFICATORE PASSA-ALTO
Z 1 (s ) = R1 +
Av ( s ) = −
dove
G. Martines
1
sC
Z 2 (s ) = R2
Z2
sR2 C
R
=−
=− 2
Z1
sR1C + 1
R1
Ao = −
R2
R1
e
s
s+
1
R1C
=
Ao s
s + ωL
ω L = 2πf L =
1
R1C
45
INTEGRATORE DI MILLER
G. Martines
46
DERIVATORE
G. Martines
47