PRINCIPIO DI RELATIVITA’ GALILEIANA
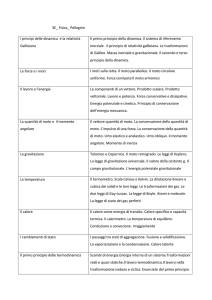
Un evento è qualcosa che accade indipendentemente dal sistema di riferimento che potremmo usare per descriverlo. L’evento accade
in un punto nello spazio e in un istante nel tempo. Si considerino due terne cartesiane S e S ′ , con la seconda in moto relativo rispetto
alla prima con velocità v (costante) nella direzione positiva dell’asse delle x della prima. Il principio di relatività classico può essere
alternativamente formulato dicendo che le leggi della meccanica sono invarianti per trasformazioni galileiane, intendendo come tali la
seguente trasformazione di coordinate:
Posizione
x ′ = x − vt
y′ = y
z′ = z
t′ = t
Velocità
′
dx
dx
=
− v → u′x = ux − v
dt
dt
dy ′ dy
=
→ u′y = uy
dt
dt
dz ′ dz
=
→ u′z = uz
dt
dt
u′ = u − v
Accelerazione
2 ′
2
d x
d x
= 2 → a′x = a x
dt 2
dt
2 ′
d y
d2 y
=
→ a′y = a y
dt 2
dt 2
d2 z ′ d2 z
= 2 → a′z = a z
dt 2
dt
′
a =a
Da queste equazioni segue subito che l’intervallo
di tempo fra gli avvenimenti di due dati eventi, P e
Q, è lo stesso per ogni osservatore
cioè t ′P − t ′Q = t P − t Q e che la distanza, o
intervallo spaziale, fra due punti, A e B, misurata
ad un dato istante, è lo stesso per ogni
osservatore, cioè xB′ − xA′ = xB − xA . Infatti se A e
B sono gli estremi di un’asta solidale con il
riferimento S per l’osservatore accentato S’ essa
xB′ = xB − v ∙ t B
e sottraendo membro a membro xB′ − xA′ = xB − xA − v(t B − t A ) ma poiché le
xA′ = xA − v ∙ t A
posizioni degli estremi A e B sono misurate allo stesso istante, si ha che t B = t A e di conseguenza xB′ − xA′ = xB − xA
avrà una velocità – v per cui si avrà:
Secondo le trasformazioni di Galileo le misure di intervalli spaziali e temporali sono ASSOLUTE, cioè forniscono gli stessi risultati per tutti
gli osservatori inerziali in quanto la velocità relativa dei riferimenti è del tutto arbitraria e non interviene nei risultati.
Nella fisica classica, anche la massa non è influenzata dal moto del sistema di riferimento quindi, il prodotto m ∙ a sarà lo stesso per tutti
gli osservatori inerziali. Le leggi del moto di Newton e le equazioni del moto di una particella sono esattamente le stesse in tutti i sistemi
di riferimento inerziali. Non ci sono sistemi di riferimento privilegiati. Due orologi posti in S e S ′ segneranno lo stesso tempo
indipendentemente dalla velocità relativa e dalle posizioni in cui sono situati gli orologi. Eventi simultanei in S sono, pertanto,
simultanei in S ′ .
Si consideri quanto illustrato in figura. Dal centro di una
stanza vengono lanciate due biglie, con velocità vp in
direzioni opposte, verso le pareti. Un osservatore A
solidale con la stanza vedrà le due biglie raggiungere le
pareti simultaneamente. Consideriamo ora la situazione
dal punto di vista di un osservatore esterno B, in moto
verso sinistra con velocità v < 𝑣p . Esso vedrà la parete
sinistra avvicinarsi verso di lui con velocità v, e, poiché
valgono le regole della meccanica, la pallina, che si muove
verso sinistra, possiede per l’osservatore B una velocità
vs = vp − v mentre la parete di destra si allontanerà con
velocità v da B, che vedrà la pallina lanciata verso destra
muoversi con velocità vd = vp + v per cui i tempi t s e t d
impiegati dalle palline per raggiungere, rispettivamente, la parete sinistra e destra, risultano essere t s =
ts = td =
l
vp
l
v s +v
e td =
l
v d −v
quindi
quindi le biglie raggiungeranno simultaneamente le pareti di destra e di sinistra. La simultaneità degli eventi poggia
sull’assunto che valga la legge di composizione delle velocità, implicita nel principio di relatività Galileiana.
ELETTROMAGNETISMO E NON INVARIANZA PER TRASFORMAZIONI GALILEIANE
Leggi di Maxwell: Elettromagnetismo (1862).
Le equazioni di Maxwell mostrano che il campo elettromagnetico verifica le equazioni delle
onde e che la velocità di propagazione è data da:
𝑐=
1
𝜀0 ∙ 𝜇0
= 299792458 𝑚/𝑠
La teoria ondulatoria prevede che le onde si propaghino in un mezzo e che la velocità delle
onde è riferita a tale mezzo di propagazione. Maxwell aveva notato che il valore della velocità
propagazione delle onde elettromagnetiche era molto vicina a quella della luce.
di
Al “mezzo” di propagazione delle onde fu dato storicamente il nome di “etere”. Nel 19° secolo la visione meccanica della fisica non
ammetteva che un’onda si potesse propagare nello spazio vuoto. Un osservatore solidale con l’etere misura per la luce una velocità pari
a𝑐
=
1
𝜀 0 ∙𝜇 0
mentre un qualunque altro osservatore in moto relativo ad esso con velocità 𝑣 misurerà una velocità pari a 𝑐 ± 𝑣.Quindi
la luce non è invariante per trasformazioni di Galileo e questo comporta l’esistenza di un riferimento privilegiato rispetto al quale la luce
viaggia con velocità c in contrasto con i postulati della meccanica che non ammettono un sistema privilegiato.
Alla fine del 19° secolo i fisici si sono trovati a dover scegliere fra le seguenti possibilità:
1.
2.
3.
Esiste un principio di relatività per la meccanica ma non per l’elettrodinamica; nell’elettrodinamica esiste un riferimento inerziale
privilegiato che è quello dell’etere.
Esiste un principio di relatività sia per la meccanica che per l’elettrodinamica, ma le leggi dell'elettrodinamica date da Maxwell non
sono corrette. Se questa alternativa fosse corretta, noi dovremmo essere in grado di eseguire esperimenti che mostrano deviazioni
dall’elettrodinamica di Maxwell, e riformulare le leggi dell'elettromagnetismo. Le trasformazioni di Galileo sarebbero applicabili
anche in questo caso.
Esiste un principio di relatività sia per la meccanica che per l’elettrodinamica ma le leggi della meccanica date da Newton non sono
corrette. Se questa alternativa è quella giusta, dovremmo essere in grado di eseguire esperimenti che mostrano deviazioni dalla
meccanica Newtoniana e riformulare le leggi della meccanica. In questo caso, le leggi di trasformazione corrette non sarebbero
quelle di Galileo (poiché esse non sono consistenti con l'invarianza delle equazioni di Maxwell) ma delle altre che siano consistenti
con l'elettromagnetismo classico e la nuova meccanica.
Gli esperimenti dimostrano effettivamente che la meccanica Newtoniana non fornisce previsioni corrette quando viene applicata a
particelle che si muovono con velocità vicina a quella della luce. Infatti, nella meccanica newtoniana, non c'è in linea di principio alcun
limite alla velocità raggiungibile da una particella, così che la velocità della luce c non gioca affatto un ruolo speciale. Un elettrone
accelerato da una d.d.p. di 10 Mev raggiunge una velocità di 0.9988 c. Tuttavia, se l'energia dell'elettrone da 10 Mev viene aumentata
di un fattore quattro (a 40 Mev) l’esperienza mostra che la velocità non si raddoppia a 1,9976 c, come ci si potrebbe aspettare dalla
1
relazione classica 𝐸𝑐 = 𝑚𝑣 2 , ma rimane inferiore a c; essa cresce solamente da 0,9988 c a 0,9999 c, con una variazione dello 0,11 %.
2
Tutti i tentativi fatti per preservare un riferimento assoluto(etere) fallirono e tra le tre possibili alternative, la terza si è dimostrata quella
corretta.
POSTULATI DELLA RELATIVITA’
1)
2)
Le leggi della fisica sono le stesse in tutti i sistemi inerziali, non esiste un sistema inerziale privilegiato (Principio di relatività).
La velocità della luce nel vuoto ha lo stesso valore c in tutti i sistemi inerziali. (Principio della costanza delta velocità delta luce).
II principio di relatività di Einstein va al di là del principio di relatività Newtoniana, che si riferiva solo alle leggi della meccanica, per
includere tutte le leggi della fisica. Esso afferma che è impossibile, per mezzo di qualsiasi misura fisica, definire un sistema inerziale
come intrinsecamente in quiete o in moto; si può solo parlare del moto relativo dei due sistemi.
CONCETTO DI SIMULTANEITA’
Si consideri una sorgente M al centro di un vagone di lunghezza 𝐿′ .
All’istante 𝑡 ′ =0 la sorgente emette due fasci di luce dirigendoli verso
le pareti A e B del vagone (fig. 1).
I due fasci raggiungono contemporaneamente le pareti A e B
𝐿′
all’istante 𝑡𝐴′ = 𝑡𝐵′ = 2𝑐 (fig. 2). Quando i due fasci di luce
raggiungono le pareti vengono riflessi verso la sorgente M (fig. 3). I
due fasci ritornano contemporaneamente sulla sorgente M dopo la
′
′
riflessione, al tempo 𝑡𝑀𝐴𝑀
= 𝑡𝑀𝐵𝑀
. Per l’ osservatore S’ solidale con
treno I due fasci arrivano simultaneamente sulle pareti e
simultaneamente sulla sorgente. I due eventi però sono differenti
per un aspetto: nel primo caso i due fenomeni avvengono in punti
diversi, le pareti, mentre nel secondo caso avvengono nello stesso
punto, la sorgente.
Immaginiamo ora che il treno sia in moto con velocità 𝑣 rispetto al
binario (fig. 4 - Osservatore S(xy)).
Fig. 1
il
Fig. 2
In base al principio di relatività possiamo affermare che per
l’osservatore S’, solidale con il treno, non cambia nulla: i due fasci
arriveranno contemporaneamente prima sulle pareti e poi sulla
sorgente.
Fig. 3
Fig. 4
Fig. 5
Cosa si può dire per l’osservatore S? (fig. 5)
La lunghezza del vagone vista dall’osservatore S si determina
𝐿′
mediante la formula 𝐿 = 𝛾 .
La legge orario per il fascio di luce rispetto all’osservatore S è:
𝐿
𝑋𝑙𝑢𝑐𝑒 = 2 − 𝑐𝑡 mentre per la parete A si ha 𝑋𝐴 = 𝑣𝑡 per cui la luce raggiungerà la parete A quando 𝑋𝑙𝑢𝑐𝑒 =
𝑋𝐴 →
𝐿
− 𝑐𝑡 = 𝑣𝑡 → 𝑡𝐴 =
2
𝐿
𝐿
2
𝑐+𝑣
. Per la parete B si ha:
𝑋𝑙𝑢𝑐𝑒 = 2 + 𝑐𝑡 mentre per la parete B si ha 𝑋𝐵 = 𝐿 + 𝑣𝑡 per cui la luce raggiunge la parete B quando
𝐿
𝐿
2
𝑋𝑙𝑢𝑐𝑒 = 𝑋𝐴 → 2 + 𝑐𝑡 = 𝐿 + 𝑣𝑡 → 𝑡𝐵 = 𝑐−𝑣
.
Quindi l’arrivo dei due fasci sulle pareti è simultaneo per
l’osservatore S’ ma non per l’osservatore S. La differenza di
tempo ∆𝑡 = 𝑡𝐵 − 𝑡𝐴 è data da:
𝑡𝐵 − 𝑡𝐴 =
𝐿
2
𝑐−𝑣
−
𝐿
2
𝑐+𝑣
𝐿
=2
Quindi ∆𝒕 = 𝒕𝑩 − 𝒕𝑨 =
𝜸𝟐
𝒄𝟐
1
1
𝐿𝑣
− 𝑐+𝑣 = 𝑐 2 −𝑣 2 =
𝑐−𝑣
𝑳𝒗.
𝐿𝑣
𝑣2
1− 2
𝑐
=
𝛾2
𝑐2
𝐿𝑣.
Fig. 6
Dopo la riflessione (fig. 6) i due fasci ritornano sulla sorgente M ai tempi 𝑡𝑀𝐴𝑀 = 𝑡𝑀𝐵𝑀
Dimostriamo che 𝒕𝑴𝑨𝑴 = 𝒕𝑴𝑩𝑴
La legge oraria del fascio A, dopo la riflessione sulla parete A, è dato da:
𝐿
𝑋𝑙𝑢𝑐𝑒 = 𝑋𝐴 𝑡𝐴 + 𝑐 𝑡 − 𝑡𝐴 = 𝑣𝑡𝐴 + 𝑐(𝑡 − 𝑡𝐴 ) mentre per il punto M si ha: 𝑋𝑀 = 𝑣𝑡 + 2 .
Il fascio di luce ritorna alla sorgente M quando 𝑋𝑙𝑢𝑐𝑒 = 𝑋𝑀
→ 𝑣𝑡𝐴 + 𝑐 𝑡 − 𝑡𝐴 = 𝑣𝑡 +
𝐿
𝐿
2
si ricava 𝑡 che
rappresenta 𝑡𝑀𝐴𝑀 = 𝛾 2 𝑐
Se si ripete il calcolo per il tempo che impiega il fascio di luce per andare nel punto B e tornare in M cioè 𝑡𝑀𝐵𝑀
si ottiene lo stesso valore. Quindi I due fasci ritornano simultaneamente sulla sorgente M.
La simultaneità di due eventi è relativa. Due eventi che sono simultanei in un sistema di riferimento possono
non esserlo in un altro sistema di riferimento ma se due eventi sono simultanei in un sistema di riferimento e
avvengono nello stesso punto allora sono simultanei in tutti i sistemi di riferimento.
Vedremo ora come l’uso del solo assioma sulla invarianza della velocità della luce implichi la
dilatazione dei tempi e la contrazione delle distanze in sistemi di riferimento in moto relativo.
Consideriamo quanto mostrato in figura (orologio a luce).Un orologio a luce può essere
pensato come un dispositivo costituito da una sorgente A che manda un segnale luminoso
verso l'alto, dove, a distanza h, c’è uno specchio che riflette la luce verso il basso facendola
ritornare in A. Ogni volta che il segnale ritorna in A viene emesso un ticchettio che
rappresenta l'unità di tempo segnata dal nostro orologio. L'intervallo di tempo "base"
dell’orologio a luce sarà, dunque, il tempo impiegato dalla luce per andare da A a B e
rappresenta il tempo proprio∆𝜏 dell'orologio.
Immaginiamo ora che l’orologio sia a bordo di un treno in moto con velocità 𝑣 rispetto al
sistema del laboratorio. Alice, sul treno, misura il tempo che intercorre tra l'evento 1 e
l'evento 2, usando un solo orologio a riposo C, che registra il tempo proprio ∆𝜏0 . Bob,
guardando dalla stazione
gli eventi che si verificano
sul treno in moto, ha
bisogno di due orologi
sincronizzati, 𝐶1 e 𝐶2 , per
misurare l'intervallo di
tempo ∆𝑡 che li separa.
Per Bob i due eventi
accadono in luoghi diversi
nel suo sistema di
riferimento.
Per Alice ∆𝜏 =
2𝐷
𝑐
.La luce
viaggia alla velocità 𝑐 sia
per Bob che per Alice ma
nel riferimento di Bob la
luce percorre una distanza
maggiore pari a 2𝐿 .
2𝐿
L’intervallo di tempo tra i due eventi misurato da Bob è pari a ∆𝑡 =
dove
𝑐
𝐿=
𝐿=
1
2
1
2
∙ 𝑣 ∙ ∆𝑡
∙ 𝑣 ∙ ∆𝑡
2
2
+ 𝐷2 ricavando 𝐷 dalla ∆𝜏 =
+
1
2
2
𝑐 ∙ ∆𝜏 ma dalla ∆𝑡 =
1
1
2
2
espressioni si ha: 𝑐 ∙ ∆𝑡 =
∙ 𝑣 ∙ ∆𝑡
2
+
1
2
2𝐿
𝑐
2𝐷
𝑐
si ha:
1
si ha: 𝐿 = 𝑐 ∙ ∆𝑡 per cui uguagliando le due
2
2
𝑐 ∙ ∆𝜏 ∆𝑡
=
∆𝜏
1−
𝑣 2
𝑐
Se, rispetto a un determinato riferimento, due eventi accadono nello stesso luogo, si dice intervallo di tempo proprio l’intervallo di
tempo misurato in quel particolare sistema di riferimento. L’intervallo di tempo misurato da qualsiasi altro osservatore in altro
sistema inerziale in moto rispetto al primo è sempre maggiore dell’intervallo di tempo proprio.
∆𝑡 =
∆𝜏
1−
𝑣 2
𝑐
Il rapporto
𝑣
𝑐
= 𝛽∆𝑡 =
∆𝜏
1−𝛽 2
mentre la quantità
1
1−𝛽 2
= 𝛾per cui si scrive:∆𝑡 = 𝛾∆𝜏
La contrazione delle lunghezze è
una conseguenza diretta della
dilatazione del tempo. La lunghezza
di un oggetto misurata nel sistema
in cui l’oggetto è fermo viene
chiamata lunghezza propria 𝐿0
L’operazione di
misura della
lunghezza di un
oggetto in “quiete”
consiste nel
confronto tra
l’oggetto e l’unità
(righello). Si consideri
ora l’oggetto di cui si
vuole misurare la
lunghezza a bordo di
un vagone ferroviario in moto con velocità costante v.
Per l’osservatore S’, il carro, la penna e il righello sono in quiete e per il principio di relatività il risultato della misura è lo stesso:
L′ = L0 .
Nel sistema di riferimento S la misura della lunghezza della penna viene fatta in questo modo: si posizione un traguardo fisso T nel
sistema S e si misura l’intervallo di tempo ∆t tra il passaggio dell’estremo A e dell’estremo B sul traguardo T.
𝐿 = 𝑣∆𝑡.
(1)
L’osservatore S’ vede il traguardo muoversi a velocità – 𝑣. Per misura la
lunghezza a riposo della penna facendo uso del traguardo procede in
questo modo: posiziona due orologi sincronizzati nel punto A e nel
punto B della penna e misura l’intervallo ∆𝑡 ′ tra il passaggio del
traguardo tra i due estremi A e B (∆𝑡 ′ non è un tempo proprio in quanto
misurato da due orologi diversi posti in luoghi diversi mentre ∆𝑡 lo è in
quanto misurato nello stesso punto da un solo orologio).
L′ = 𝑣∆𝑡 ′ = L0
ma ∆𝑡 ′ = 𝛾∆𝑡 → ∆𝑡 =
espressione di ∆𝑡 nella (1) si ha: 𝐿 = 𝑣
𝑳=
𝐋𝟎
𝜸
fattore
∆𝑡 ′
𝛾
∆𝑡 ′
𝛾
sostituendo
questa
ma 𝑣∆𝑡 ′ = L′ = L0 per cui
. La lunghezza di un oggetto misurata da un osservatore in moto rettilineo uniforme rispetto all’oggetto risulta contratta di un
1
𝛾
TRASFORMAZIONI DI LORENTZ
Si considerino due sistemi di riferimento inerziali in moto relativo aventi
l’asse 𝑋 in comune. Al tempo 𝑡 = 𝑡 ′ = 0 quando le origine coincidono
𝑂 = 𝑂′ viene emesso dall’origine un impulso luminoso che si propaga
isotropicamente in tutte le direzioni.
Per il 𝐼𝐼 ° postulato della
relatività la luce emessa si
propaga nello stesso modo nei
due sistemi di riferimento con
un fronte d’onda sferico.
P
Nel sistema di riferimento 𝑂,
dopo un intervallo di tempo ∆𝑡
il fronte d’onda descrive la sfera di raggio 𝑟 con
r
𝑟 =
𝑥 2 + 𝑦 2 + 𝑧 2 per cui vale la relazione: 𝑐 ∙ ∆𝑡 = 𝑟 → −𝑐 2 ∙ ∆𝑡 2 + 𝑟
′
′
Nel riferimento 𝑂 si ha la stessa descrizione: 𝑐 ∙ ∆𝑡 = 𝑟
′
2
→ −𝑐 ∙ ∆𝑡
′2
2
+ 𝑟
= 0.
′ 2
= 0.
Se consideriamo un punti sull’asse 𝑋 → 𝑟 = 𝑥 e dato che il raggio è stato emesso all’istante
𝑡 = 𝑡 ′ = 0 → ∆𝑡 = 𝑡; ∆𝑡 ′ = 𝑡 ′ ; ∆𝑥 = 𝑥 𝑒 ∆𝑥 ′ = 𝑥 ′ .
Le trasformazioni desiderate devono essere del tipo: 𝑥 ′ = 𝑥 ′ 𝑥, 𝑦, 𝑧, 𝑡 ; 𝑦 ′ = 𝑦 ′ 𝑥, 𝑦, 𝑧, 𝑡 ; 𝑧 ′ = 𝑧 ′ 𝑥, 𝑦, 𝑧, 𝑡 ;𝑡 ′ = 𝑡 ′ 𝑥, 𝑦, 𝑧, 𝑡 tali per
cui sia valida la relazione ∆𝑆 2 = −𝑐 2 ∙ 𝑡 2 + 𝑥 2 + 𝑦 2 + 𝑧 2 (invariante relativistico).
𝑥 ′ = 𝛾 𝑥 − 𝛽𝑐𝑡
𝑐𝑡 ′ = 𝛾 𝑐𝑡 − 𝛽𝑥
𝑦′ = 𝑦
𝑧′ = 𝑧
Le trasformazioni richieste devono ridursi a quelle Galileiane per 𝑣 ≪C in quanto funzionano
molto bene in tale regime.
le trasformazioni inverse sono:
𝑥 = 𝛾 𝑥 ′ + 𝛽𝑐𝑡 ′
𝑐𝑡 = 𝛾 𝑐𝑡 ′ + 𝛽𝑥 ′
𝑦 = 𝑦′
𝑧 = 𝑧′
Le trasformazioni richieste devono essere lineari per preservare l’omogeneità di spazio e
tempo nelle direzioni ortogonali al moto 𝑦 ′ = 𝑦 𝑒 𝑧 ′ = 𝑧
Dalle trasformazioni di Lorentz seguono direttamente alcune proprietà del mondo
relativistico:
DILATAZIONE DEI TEMPI
Si consideri una coppia di eventi (punti nello spazio tempo) 𝑡1′ , 𝑥0′ e 𝑡2′ , 𝑥0′ nel SR 𝑂′ . Questi
due eventi rappresentano due tempi segnati da un orologio posto in 𝑥0′ e in quiete nel SR 𝑂′ . La distanza temporale tra questi due
eventi è: ∆𝑇 ′ = 𝑡2′ − 𝑡1′ .
Nel SR 𝑂, i due eventi sono descritti da 𝑡1 , 𝑥1 , 𝑡2 , 𝑥2 con:
𝑡1 , 𝑥1 𝑐𝑡1 = 𝛾 𝑐𝑡1′ + 𝛽𝑥0′
𝑥1 = 𝛾 𝑥0′ + 𝛽𝑐𝑡1′ e
𝑡2 , 𝑥2 𝑐𝑡2 = 𝛾 𝑐𝑡2′ + 𝛽𝑥0′
𝑥2 = 𝛾 𝑥0′ + 𝛽𝑐𝑡2′
𝛾
𝛾
Per cui ∆𝑇 = 𝑡2 − 𝑡1 = 𝑐 𝑐𝑡2′ + 𝛽𝑥0′ − 𝑐 𝑐𝑡1′ + 𝛽𝑥0′ = 𝛾 𝑡2′ − 𝑡1′ = 𝛾∆𝑇 ′
𝑣
Quindi ∆𝑇 = 𝛾∆𝑇′ cioè l’intervallo di tempo misurato nel SR in cui l’orologio è in moto
è più grande del tempo misurato a riposo (tempo proprio).
CONTRAZIONE DELLELUNGHEZZE
𝑂
𝑂′
𝑥1′ = 𝑂′ 𝑥2′ = 𝐿𝑜
Si consideri una sbarra rigida di lunghezza 𝐿0 a riposo nel SR 𝑂′ . I suoi estremi si trovano
per ogni tempo 𝑡 ′ nei punti 𝑥1′ = 0, 𝑥2′ = 𝐿0 .
Tali posizioni sono legate a quelle del SR 𝑂 mediante le TL:
𝑥1′
𝑥2′
= 𝛾 𝑥1 − 𝑣𝑡1
= 𝛾 𝑥2 − 𝑣𝑡2
Misurare la lunghezza della sbarra nel SR 𝑂 significa valutare 𝑥2 − 𝑥1 quando
𝑡1 = 𝑡2 = 𝑡 quindi si ha: 𝐿0 = 𝑥2′ − 𝑥1′ =
Cioè 𝐿 =
𝐿0
𝛾
𝛾 𝑥2 − 𝑣𝑡 − 𝛾 𝑥1 − 𝑣𝑡 = 𝛾 𝑥2 − 𝑥2 = 𝛾𝐿
. La lunghezza 𝐿dell’asta misurata nel sistema di riferimento in cui essa è in moto è minore di quella misurata nel sistema di
riferimento in cui essa è a riposo.
COMPOSIZIONE RELATIVISTICA DELLE VELOCITA’
𝑌′
𝑌
𝑣
2
∆𝑌 ′ = ∆𝑌
𝑢′
1
∆𝑋 ′
𝑂′
𝑂
𝑋 ≡ 𝑋′
𝑢′ nel riferimento 𝑂′ (in moto con velocità 𝒗 rispetto al riferimento 𝑂).
Si consideri un punto materiale in moto con velocità
𝑢𝑥 =
Le componenti della velocità rispetto al riferimento 𝑂 sono:
𝑢𝑥′ =
Le componenti della velocità rispetto al riferimento 𝑂′ sono:
𝑑𝑥 𝑡
𝑑𝑡
;
𝑑𝑥 ′ 𝑡 ′
𝑑𝑡 ′
𝑢𝑦 =
𝑢𝑦′ =
;
𝑑𝑦 𝑡
𝑑𝑡
𝑑𝑦 ′ 𝑡 ′
𝑑𝑡 ′
;
𝑢𝑧 =
;
𝑢𝑧′ =
𝑑𝑧 𝑡
𝑑𝑡
𝑑𝑧 ′ 𝑡 ′
𝑑𝑡 ′
Le trasformazioni di Lorentz sono:
𝑥 = 𝛾 𝑥 ′ + 𝛽𝑐𝑡 ′
𝑦 = 𝑦′
𝑧 = 𝑧′
𝑐𝑡 = 𝛾 𝑐𝑡 ′ + 𝛽𝑥 ′
Dalle trasformazioni di Lorentz si ha:
𝑑𝑥 = 𝛾 𝑑𝑥 ′ + 𝛽𝑐𝑑𝑡 ′ = 𝛾
𝑑𝑦 = 𝑑𝑦 ′ =
𝑑𝑥 ′
+ 𝛽𝑐 𝑑𝑡 ′ = 𝛾 𝑢𝑥′ + 𝛽𝑐 𝑑𝑡 ′
𝑑𝑡 ′
𝑑𝑦 ′ ′
𝑑𝑡 = 𝑢𝑦′ 𝑑𝑡 ′
𝑑𝑡 ′
𝑑𝑧 ′ ′
𝑑𝑧 = 𝑑𝑧 = ′ 𝑑𝑡 = 𝑢𝑧′ 𝑑𝑡 ′
𝑑𝑡
′
→
𝑑𝑦 = 𝑢𝑦′ 𝑑𝑡 ′
→
𝑑𝑧 = 𝑢𝑧′ 𝑑𝑡 ′
𝑐𝑑𝑡 = 𝛾 𝑐𝑑𝑡 ′ + 𝛽𝑑𝑥 ′ = 𝛾 𝑐 + 𝛽
𝑢𝑥 =
𝑢𝑥 =
𝑢𝑦 =
𝑢𝑧 =
𝑑𝑥 𝑡
𝑑𝑡
𝑐+𝛽𝑢 𝑥′
𝑑𝑦 𝑡
𝑑𝑡
𝑑𝑧 𝑡
𝑑𝑡
𝑑𝑥 ′
𝑑𝑡 ′ = 𝛾 𝑐 + 𝛽𝑢𝑥′ 𝑑𝑡 ′ →
𝑑𝑡 ′
𝑑𝑡 ′
𝑐+𝛽𝑢 𝑥′
𝑐+𝛽𝑢 𝑥′ 𝑑𝑡 ′
𝑐
𝑐
𝑐 𝑢 𝑥′ +𝛽𝑐
𝑢 𝑦′ 𝑑𝑡 ′
=𝛾
=𝛾
=
𝑢 𝑧′ 𝑑𝑡 ′
𝑐+𝛽𝑢 𝑥′ 𝑑𝑡 ′
=𝛾
=𝛾
=
𝑢 𝑥′ +𝛽𝑐
𝛽
1+ 𝑢 𝑥′
𝑐
𝑐𝑢 𝑦′
𝑐+𝛽 𝑢 𝑥′
𝑐𝑢 𝑧′
𝑢𝑥 =
1
=𝛾
1
𝑐+𝛽 𝑢 𝑥′
=𝛾
𝑢 𝑥′ +𝛽𝑐
𝛽
1+ 𝑢 𝑥′
𝑐
𝑑𝑡 =
𝛾
𝑐 + 𝛽𝑢𝑥′ 𝑑𝑡 ′
𝑐
𝑢 𝑦′
𝛽
𝑐
1+ 𝑢 𝑥′
𝑢 𝑧′
𝛽
1+ 𝑢 𝑥′
𝑐
𝑣
ma 𝛽 = 𝑐 quindi si può ance scrivere: 𝑢𝑥 =
𝑣
ma 𝛽 = 𝑐 quindi si può ance scrivere:
𝑣
ma 𝛽 = 𝑐 quindi si può ance scrivere:
Le trasformazioni inverse sono:
𝑢𝑥′ =
𝑑𝑥 = 𝛾 𝑢𝑥′ + 𝛽𝑐 𝑑𝑡 ′
sostituendo sia al numeratore che al denominatore le espressioni ricavate sopra si ha:
𝛾 𝑢 𝑥′ +𝛽𝑐 𝑑𝑡 ′
𝛾
𝑐
→
𝑢 𝑥 −𝑣
𝑣
1− 2 𝑢 𝑥
𝑐
;
𝑢𝑦′ =
1
𝑢𝑦
𝛾
𝑣
1− 2 𝑢 𝑥
𝑐
;
𝑢𝑧′ =
1
𝑢𝑧
𝑣
𝛾 1− 2 𝑢 𝑥
𝑐
𝑢𝑦 =
𝑢𝑧 =
𝑢′𝑥 +𝑣
𝑣
1+ 2𝑢′𝑥
𝑐
1
𝑢 𝑦′
𝑣
𝛾 1+ 2 𝑢 𝑥′
𝑐
1
𝑢 𝑧′
𝑣
𝛾 1+ 2 𝑢 𝑥′
𝑐
OSSERVAZIONE:
Le componenti della velocità, a differenza delle
lunghezze trasverse alla direzione di moto, vengono
influenzate dal moto relativo dei riferimenti a causa
della variabile tempo.
RAPPRESENTAZIONE GEOMETRICA DELLO SPAZIO TEMPO (Diagrammi spazio-temporali di minkowski)
Asse temporale
𝑐𝑡
Linea di universo della luce
Linea di universo della luce
Linea di universo di un
generico punto materiale
Linea di universo di un punto
materiale fermo a distanza
dall’origine
𝑂
𝑑
𝑥
𝑑
Asse
spaziale
𝑂 del riferimento
Il diagramma di Minkowski riporta nell’asse orizzontale la coordinata
spaziale 𝒙 e nell’asse verticale y la coordinata temporale (moltiplicata
per la velocità della luce 𝒄). Le bisettrici rappresentano le linee di
universo di un raggio di luce.
𝑐𝑡
𝑏
La “distanza” o metrica tra due punti evento nel diagramma di
Minkowski
è data da: ∆s 2 = c 2 ∆t 2 − ∆x 2
In termini infinitesimi: ds 2 = c 2 dt 2 − dx 2
La distanza, a causa del segno meno, può assumere valori positivi
negativi o nulli.
∆𝑆
∆𝑦 = 𝑐∆𝑡
𝑎
𝑂
∆𝑥
Diagramma di Minkowski: a sinistra considerando una sola dimensione spaziale, a destra considerate due dimensioni spaziali.
𝑥
All’interno della regione (cono) aOc si ha 𝒄𝟐 𝒅𝒕𝟐 − 𝒅𝒙𝟐 > 0, cioè l’intervallo tra il generico evento (x, t) e l’evento (0, 0) è di tipo
tempo. In tale regione t > 0, cioè ogni evento ha luogo dopo l’evento O. Poiché due eventi, separati da un intervallo di tipo tempo,
non possono mai essere simultanei in alcun riferimento inerziale, non è possibile scegliere un sistema di riferimento in cui un
arbitrario evento, posto all’interno della regione aOc, abbia luogo prima di O, cioè avvenga al tempo t < 0. Tutti gli eventi all’interno di
aOc sono, allora, posteriori a O, fanno cioè parte della regione del futuro assoluto. Nello stesso modo si può osservare che ogni
evento posto in dOb avviene prima dell’evento O, e questo è vero in qualunque riferimento inerziale. La regione dOb è detta appunto
del passato assoluto (cono del passato). Gli eventi posti nel passato e nel futuro possono essere messi in relazione causale con
l’evento O.
Gli eventi all’interno delle regioni aOd e cOb verificano la condizione 𝒅𝒙𝟐 > 𝒄𝟐 𝒅𝒕𝟐 quindi sono separati dall’evento O da un intervallo
di tipo spazio. Se D è un evento in tali regioni, si può sempre trovare un riferimento inerziale in cui D e O sono simultanei, anche se
non possono mai avvenire nello stesso luogo per alcun riferimento. Esistono sistemi di riferimento in cui D avviene prima di O e altri in
cui avviene dopo. La regione tra il cono del futuro e il cono del passato è indicata come il presente di O (o anche come l’altrove
assoluto di O, perché, come abbiamo detto, in nessun sistema di riferimento un evento, che appartiene a questa regione, e l’evento O
possono verificarsi nello stesso luogo). Gli eventi posti lungo le bisettrici, per i quali vale la relazione 𝒅𝒙𝟐 = 𝒄𝟐 𝒅𝒕𝟐 , appartengono al
cono-luce e sono connessi per l’appunto all’evento O da segnali luminosi. Tali eventi sono detti eventi di tipo luce.
L’asse 𝑐𝑡 ′ del riferimento 𝑂′ corrisponde agli eventi per i quali
𝑥 ′ = 0. Dalle trasformazioni di Lorentz si ha:
𝑋 ′ = 𝛾 𝑋 − 𝛽𝑐𝑡 → 𝑋 ′ = 0 → 𝛾 𝑋 − 𝛽𝑐𝑡 = 0 → 𝑋 = 𝛽𝑐𝑡 ma 𝛽 =
𝑣
𝑥′ = 0
𝑥 = 𝛽𝑐𝑡 = 𝑣𝑡
𝑐𝑡 ′
𝑐𝑡
𝑐
Quindi 𝑿 = 𝒗𝒕
L’asse 𝑥 ′ del riferimento 𝑂′ corrisponde agli eventi per i quali
𝑐𝑡 ′ = 0. Dalle trasformazioni di Lorentz si ha:
𝑐𝑡 ′ = 𝛾 𝑐𝑡 − 𝛽𝑋 → 𝑐𝑡 ′ = 0 → 𝛾 𝑐𝑡 − 𝛽𝑋 = 0 → 𝑐𝑡 = 𝛽𝑥 → tan 𝜃 = 𝛽
Quindi𝐭𝐚𝐧 𝜽 = 𝜷
Le equazioni di Lorentz trasformano un sistemo di riferimento
ortogonale 𝑂 in un sistema di riferimento non ortogonale 𝑂′ in
cui l’angolo 𝜃 è dato da: 𝜃 = tan−1 𝛽. Il valore massimo che 𝜃
𝜋
può assumere è pari a 𝜃 = e lo si ha in corrispondenza ad una
4
velocità pari a 𝑐.
Il punto 𝑃1 si ottiene intersecando il ramo
destro dell’iperbole di calibrazione
𝑥 2 − 𝑐𝑡 2 = 1 con l’asse 𝑥 ′ rappresentato
dall’equazione 𝑐𝑡 = 𝛽𝑥
𝑥 2 − 𝑐𝑡 2 = 1 → 𝑥 2 − 𝛽𝑥 2 = 1
𝑐𝑡 = 𝛽𝑥
1
𝑥 2 1 − 𝛽2 = 1 → 𝑥 2 =
𝑥 2 − 𝑐𝑡
1 − 𝛽2
𝑐𝑡 = 𝛽𝑥
1
𝑥=
=𝛾
𝑥=𝛾
→ 𝑐𝑡 = 𝛽𝛾
1 − 𝛽2
𝑐𝑡 = 𝛽𝑥
𝑃1 ≡ 𝛾; 𝛽𝛾
Allo stesso modo si ricavano le coordinate del
punto 𝑃2
𝑃2 ≡ 𝛽𝛾; 𝛾
𝑐𝑡 ′ = 0
𝑐𝑡 = 𝛽𝑥
𝜃
𝑥′
𝑂
𝜃
𝑥
𝑂′
𝑐𝑡 ′ 𝑥 ′ = 0
𝑐𝑡
𝑐𝑡
2
2
− 𝑥2 = 1
=1
Iperbole di calibrazione
𝑥 2 − 𝑐𝑡
𝑃2
1
1
1−𝛽
′
2 quindi si ha: 𝑥 =
1
1−𝛽 2
2
1 − 𝛽2 =
1
𝑂 ≡ 𝑂′
𝑐𝑡
1
1−𝛽 2
=1
𝑥 ′ 𝑐𝑡′ = 0
𝑃1
2
𝑥
− 𝑥2 = 1
Sostituendo le coordinate del punto 𝑃1 ≡ 𝛾; 𝛽𝛾 nelle trasformazioni di Lorentz 𝑥 ′
𝑥 ′ = 𝛾 𝛽𝛾 − 𝛽 2 𝛾
𝑥 ′ = 𝛾 2 − 𝛽2 𝛾 2 = 𝛾 2 1 − 𝛽2
ma 𝛾 =
2
= 𝛾 𝑥 − 𝛽𝑐𝑡 ha: 𝑥 ′ = 𝛾 𝛽𝛾 − 𝛽𝛽𝛾
1 − 𝛽2 = 1
𝑥 ′ = 1 quindi il punto 𝑃1 rappresenta l’unità di lunghezza per l’asse 𝑐𝑡 ′ nel riferimento 𝑂′
Analogamente il punto 𝑃2 rappresenta l’unità di lunghezza per l’asse 𝑥 ′ nel riferimento 𝑂′
Il significato delle curve di calibrazione è il seguente:
Si consideri come esempio l’iperbole superiore: 𝑐𝑡
ma
𝑥2
𝑡2
= 𝑣 2 per cui
𝑥2
𝑡 2𝑐2
2
− 𝑥2 = 1 → 𝑐2 𝑡 2 −
𝑥2
𝑐2
= 1 → 𝑐2 𝑡 2 1 −
𝑥2
𝑡 2𝑐2
=1
= 𝛽 2 quindi si ha: 𝑐 2 𝑡 2 1 − 𝛽 2 = 1 𝑚𝑎 𝑡 2 1 − 𝛽 2 = 𝜏 2 𝑝𝑒𝑟 𝑐𝑢𝑖 𝑠𝑖 𝑎: 𝑐 2 𝜏 2 = 1 che rappresenta l’unità di
tempo nel sistema di riferimento 𝑂′ .
La figura a lato mostra come localizzare un evento in un sistema di riferimento.
Si può notare che gli eventi 𝑃1 e 𝑃2 simultanei nel sistema di riferimento 𝑂 non
sono simultanei nel riferimento 𝑂′
Possiamo usare la rappresentazione geometrica spazio-tempo anche per
comprendere l’ordine temporale e la separazione spaziale degli eventi.
𝑐𝑡 ′
𝑐𝑡
𝑃1
𝑃2
𝑃
𝑄
𝑥′
𝑂 ≡ 𝑂′
𝑂 ′
𝑂
𝑥
Si consideri l’area verde della figura a lato: per un punto
qualunque 𝑷 di questa area, limitata dalle linee di universo delle
onde luminose, possiamo tracciare l’asse 𝑐𝑡 ′ che passa per
l’origine. Cioè noi possiamo trovare un riferimento inerziale S’ in
cui gli eventi 𝑶 e 𝑷 avvengono nello stesso luogo 𝑥 ′ = 0 e
sono distanziati nel tempo. L’evento 𝑷 segue nel tempo l’evento
𝑶 (avviene più tardi per gli orologi di S’), qualunque sia la sua
posizione nella metà superiore dell’area verde. Quindi gli eventi nella parte superiore sono assolutamente nel futuro rispetto 𝑶 e
questa regione è chiamata futuro Assoluto. Se invece all’evento 𝑷 corrisponde un punto spazio-temporale nella metà inferiore
dell’area verde, 𝑷 precederà nel tempo l’evento 𝑶. Gli eventi della metà inferiore sono assolutamente nelpassato rispetto ad 𝑶, e
questa regione è chiamata passato assoluto.
Nelle regioni color verde perciò esiste un determinato ordine temporale degli eventi rispetto 𝑶 poiché si può sempre trovare un
riferimento in cui 𝑶 e 𝑷 avvengono nello stesso luogo; un unico orologio determinerà in modo assoluto l’ordine temporale dell’evento
in quel luogo. Consideriamo ora le regioni bianche della figura. Per un qualunque punto 𝑸 possiamo tracciare l’asse 𝑥 ′ che passi
dall’origine, cioè possiamo trovare un riferimento inerziale S’ in cui 𝑶 e 𝑸 avvengono nello stesso tempo e sono distanziati solo nello
spazio. Possiamo sempre trovare un riferimento inerziale in cui gli eventi 𝑶 e 𝑸 appaiono simultanei per punti spazio-temporali 𝑸 che
si trovano nelle regioni bianche della figura, e perciò questa regione è chiamata presente. In altri riferimenti inerziali naturalmente 𝑶
e 𝑸 non sono simultanei e non c’è un ordine temporale assoluto di questi eventi ma solo un ordine temporale relativo.
Se ricerchiamo la separazione spaziale degli eventi, invece del loro ordine temporale, vediamo che gli eventi nel presente sono
distanziati in modo assoluto da 𝑶, mentre quelli nel futuro assoluto o nel passato assoluto non hanno un definito ordine spaziale
rispetto a 𝑶. Infatti le regioni Passato e Futuro Assoluto sono dette di tipo temporali, mentre la regione Presente è detta di tipo
spaziale.
DINAMICA RELATIVISTICA
La dinamica classica o Newtoniana non è compatibile con le trasformazioni di Lorentz. Essa infatti ammette forze che possono
accelerare corpi a velocità indefinita e ammette forze di azione a distanza in cui il principio di azione e reazione non ha alcun
significato tranne per le forze di contatto. Se si effettua l’analisi di un processo d’urto da due riferimenti in moto relativo si osserva
che la conservazione dell’impulso (quantità di moto) non è sempre valida (dipende dal riferimento scelto) e questo contraddice il
postulato fondamentale della relatività ristretta che afferma che le leggi della fisica sono le stesse in tutti i riferimenti inerziali. Per
questi e altri motivi occorre ridefinire i concetti di impulso (quantità di moto), energia cinetica ecc…
Gli esperimenti indicano che la legge del moto corretta è: 𝑭 =
𝒅
𝒅𝒕
𝒒 (detta equazione di Minkowski) dove 𝒒 = 𝜸𝒎𝒗 rappresenta la
nuova definizione di impulso o quantità di moto relativistica. La massa si considera un invariante relativistico al pari dell’invariante
relativistico spazio-temporale.
Anche nella Relatività è valido il Teorema del lavoro: ∆𝐸𝑐 = 𝐿 = 𝐹 ∙ ∆𝑆 (in termini infinitesimali : 𝑑𝐸𝑐 = 𝑑𝐿 = 𝐹 ∙ 𝑑𝑆)
𝑑𝐸𝑐
𝑑𝑡
=𝐹∙
𝑑𝑆
𝑑𝑡
= 𝐹 ∙ 𝑣 ma 𝑭 =
𝒅
𝒅𝒕
𝜸𝒎𝒗 con 𝛾 funzione della velocità per cui si ha:
𝑑 𝐸𝑐
𝑑𝑡
=
𝑑
𝑑𝑡
𝛾𝑚𝑣 ∙ 𝑣.
Sviluppando i passaggi (si veda Vincenzo Barone- Relatività : principi e applicazioni – Bollati Boringhieri) si arriva a scrivere per l’energia cinetica la
relazione: 𝐸𝑐 = 𝑚𝑐 2 𝛾 − 1 dove 𝑚 rappresenta la massa a riposo del corpo.
Dall’analisi della relazione 𝐸𝑐 = 𝛾𝑚𝑐 2 − 𝑚𝑐 2 si può notare che il primo termine dipende dalla velocità del corpo 𝛾 mentre il
secondo è indipendente da 𝑣. Se un corpo è dotato di massa possiede un’energia pari a 𝒎𝒄𝟐 chiamata energia intrinseca del corpo.
Riscrivendo la relazione dell’energia cinetica in questo modo: 𝐸𝑐 = 𝛾𝑚𝑐 2 − 𝑚𝑐 2 → 𝛾𝑚𝑐 2 = 𝑚𝑐 2 + 𝐸𝑐 .
Un corpo dotato di massa e avente una determinata velocità possiede un’energia totale 𝐸 = 𝛾𝑚𝑐 2 = 𝑚𝑐 2 + 𝐸𝑐
Quest’ultima relazione mostra l’equivalenza tra massa ed energia di un corpo.
Si considerino nuovamente le relazione 𝒒 = 𝜸𝒎𝒗 (quantità di moto relativistica) e 𝑬 = 𝜸𝒎𝒄𝟐 (energia totale).
𝒒 = 𝜸𝒎𝒗
𝑬 = 𝜸𝒎𝒄𝟐
Se si moltiplica per 𝑐 entrambi i membri si ha
𝐸 = 𝛾𝑚𝑐 2
elevando al quadrato si ha
𝑞𝑐 = 𝛾𝑚𝑣𝑐
𝐸 2 = 𝛾 2 𝑚2 𝑐 4
sottraendo membro a membro le due relazioni si ha
𝑞 2 𝑐 2 = 𝛾 2 𝑚2 𝑣 2 𝑐 2
2
𝐸 2 − 𝑞 2 𝑐 2 = 𝛾 2 𝑚2 𝑐 4 − 𝛾 2 𝑚2 𝑣 2 𝑐 2 → 𝐸 2 − 𝑞 2 𝑐 2 = 𝛾 2 𝑚2 𝑐 2 𝑐 2 − 𝑣 2 𝑚𝑎 𝛾 2 =
1
1−
2
2 2
𝑣2
𝑐2
2 4
Sviluppando si ha: 𝐸 − 𝑞 𝑐 = 𝑚 𝑐 . Questa relazione lega l’energia, la quantità di moto e la massa. Poiché la massa è un
invariante anche 𝑚2 𝑐 4 è un invariante. Ne consegue che la differenza 𝐸 2 − 𝑞 2 𝑐 2 è un invariante.
Un altro modo di scrivere la relazione tra energia, quantità di moto e massa è: 𝑬 = 𝒄 𝒒𝟐 + 𝒎𝟐 𝒄𝟐
Per un fotone 𝑚 = 0 si ha: 𝑬 = 𝒄 ∙ 𝒒 o anche
𝒒=
𝑬
𝒄
Combinando le equazioni: 𝒒 = 𝜸𝒎𝒗 e 𝑬 = 𝜸𝒎𝒄𝟐 si ricava un’espressione per la velocità di una particella in funzione dell’energia e
della quantità di moto 𝒗
=
𝒄𝟐 𝒒
𝑬
Un altro aspetto molto interessante riguarda gli urti relativistici: negli urti si conserva sempre la quantità di moto 𝒒 per cui
analizzando la relazione scritta sopra 𝐸 2 − 𝑞 2 𝑐 2 = 𝑚2 𝑐 4 si può notare che anche l’energia si conserva in quanto il termine a destra
del segno di uguaglianza è un invariante e il termine 𝑞 2 𝑐 2 , essendo 𝒒 conservata è anch’esso costante 𝐸 si conserva.
Esempio:
Dato un protone 𝑚 = 1.67 ∙ 10−27 𝑘𝑔 con quantità di moto 𝑞 = 10
sua energia cinetica e la sua velocità.
L’unità di misura della quantità di moto viene spesso misurata in
𝐺𝑒𝑉
𝑐
𝐺𝑒𝑉
𝑐
, rispetto al laboratorio, si determini la sua energia totale, la
cioè un
𝐸𝑛𝑒𝑟𝑔𝑖𝑎
𝑣𝑒𝑙𝑜𝑐𝑖𝑡 à
infatti: 𝐸 = 𝛾𝑚𝑐 2 e 𝑞 = 𝛾𝑚𝑣 se si ricava 𝛾𝑚
dalla relazione dell’energia e la si sostituisce nella relazione della quantità di moto si ha: 𝑞 =
2
𝐸
𝑐2
𝑣 →
𝐸𝑛𝑒𝑟𝑔𝑖𝑎
𝑣𝑒𝑙𝑜𝑐𝑖𝑡à
inoltre l’energia e la
massa, nella fisica delle particelle, si misurano in 𝑒𝑉 (sfruttando la relazione 𝐸 = 𝑚𝑐 ).
𝑚 = 1.67 ∙ 10−27 𝑘𝑔 → 𝑚𝑐 2 = 1,67 ∙ 10−27 ∙ 9 ∙ 1016 = 15,03 𝐽 = 0,938𝐺𝑒𝑉 → 𝑚𝑐 2 = 0,938𝐺𝑒𝑉(𝑝𝑟𝑜𝑡𝑜𝑛𝑒).
𝐸=
𝑞𝑐
2
+ 𝑚𝑐 2
2
=
10
𝐺𝑒𝑉
𝑐
𝑐
2
+ 0,938𝐺𝑒𝑉
Dalla relazione 𝐸 = 𝛾𝑚𝑐 2 è possibile ricavare 𝛾 =
2
𝐸
𝑚𝑐2
= 10,04 𝐺𝑒𝑉
=
10,04 𝐺𝑒𝑉
0,938𝐺𝑒𝑉
= 10,71 e di conseguenza 𝑣 dalla relazione 𝛾 =
Per determinare l’energia cinetica si può usare la relazione 𝐸𝑐 = 𝑚𝑐 2 𝛾 − 1
1
𝑣2
1− 2
𝑐
.
L’INERZIA DELL’ENERGIA
Si consideri un esperimento ideale in cui un corpo in moto a velocità costante viene investito da due pacchetti di radiazione
elettromagnetica. Il fenomeno viene osservato da due sistemi di riferimento: uno 𝑂′ solidale al corpo in cui il corpo è fermo e le due
onde lo investono perpendicolarmente alla direzione di moto ma con verso contrario mentre il secondo 𝑂 è un riferimento rispetto al
quale 𝑂′ si muove a velocità costante in direzione orizzontale verso destra.
𝐸
Nel riferimento 𝑂′ la quantità di moto iniziale è nulla e per
𝑞=
𝐸′
𝑐
𝑞=
Il principio di conservazione della 𝑞. 𝑑. 𝑚. sarà nulla anche dopo
𝑐
𝛼
l’assorbimento dei due fotoni. La massa M nel riferimento 𝑂′ è ferma
𝑣
𝑀
per cui continuerà a rimanere ferma.
sin 𝛼 =
Nel riferimento 𝑂 la massa M si muove verso destra con velocità 𝑣
𝑞=
e i due fotoni hanno una direzione obliqua (ricordare l’orologio a luce).
𝑀
𝑅𝑖𝑓. 𝑂
𝑣
𝑐
𝑅𝑖𝑓. 𝑂′
𝑞=
𝐸
𝑐
𝐸′
𝑐
La quantità di moto 𝑞 orizzontale prima dell’assorbimento dei due fotoni
𝐸
è data da: 𝑞 = 𝑀𝛾𝑣 + 2 sin(𝛼). Il principio di conservazione della 𝑞. 𝑑. 𝑚. resta valido per cui dopo aver assorbito la radiazione
𝑐
elettromagnetica il blocco avrà una velocità finale 𝑣𝑓 che può essere ricavata dalla seguente uguaglianza:
𝐸
𝐸
𝑣
𝑐
𝑐
𝑐
𝑀𝛾𝑓 𝑣𝑓 = 𝑀𝛾𝑣 + 2 sin 𝛼 → 𝑀𝛾𝑓 𝑣𝑓 = 𝑀𝛾𝑣 + 2 ∙
→ 𝑀𝛾𝑓 𝑣𝑓 = 𝑀𝛾𝑣 + 2
𝐸𝑣
𝑐2
ATTENZIONE
Nel riferimento 𝑂′ si è visto che la massa M continua a rimanere ferma anche dopo aver assorbito i fotoni per cui nel riferimento 𝑂′ la
velocità continuerà a rimanere la stessa (cioè la velocità non varia) 𝑣𝑓 = 𝑣. Ma se la velocità non varia in 𝑂′ deve rimanere la
stessa anche nel riferimento 𝑂 quindi riscrivendo la relazione precedente si ha: 𝑀𝛾𝑣 = 𝑀𝛾𝑣 + 2
𝐸𝑣
𝑐2
(FALSA).
Dov’è l’errore? La sola possibile via d’uscita sta nell’aver dato per scontato che la massa (INERZIA) resti la stessa. La relazione va
𝐸𝑣
𝐸
𝐸
∆𝐸
riscritta in questo modo: 𝑀𝑓 𝛾𝑣 = 𝑀𝛾𝑣 + 2 2 → 𝑀𝑓 = 𝑀 + 2 2 → 𝑀𝑓 − 𝑀 = 2 2 → ∆𝑀 = 2 dove ∆𝐸 rappresenta
𝑐
𝛾𝑐
𝛾𝑐
𝛾𝑐
l’energia trasportata dai fotoni e assorbita dalla massa M.
Se un corpo si muove con velocità 𝑣 e assorbe energia senza cambiare velocità la sua massa (INERZIA) aumenta di una quantità
∆𝐸
∆𝑀 = 2 .
𝛾𝑐
Se 𝛾 = 1 (cioè 𝑣 = 0 𝑐𝑜𝑚𝑒 𝑛𝑒𝑙 riferimento 𝑂′ ) 𝑎𝑙𝑙𝑜𝑟𝑎 ∆𝑀 =
∆𝐸
𝑐2
.
Questa relazione può essere riscritta nella nota relazione 𝐸 = 𝑀𝑐 2 se 𝑣 = 0 altrimenti: 𝐸 = 𝑀𝛾𝑐 2 .
EFFETTO DOPPLER RELATIVISTICO
L’effetto Doppler relativistico si ha ogni volta che una sorgente di onde elettromagnetiche e un osservatore sono in moto relativo.
Il fenomeno è analogo al caso delle onde meccaniche ma in questo caso la velocità di propagazione delle onde è indipendente dal
moto della sorgente ed è la stessa per tutti gli osservatori inerziali.
La relazione che consente di determinare la variazione di frequenza percepita da un osservatore in moto relativo rispetto alla
sorgente nella stessa direzione è data da:
𝑓′ = 𝑓
1±𝛽
1∓𝛽
:
𝑓 ′ : frequenza percepita dall’osservatore
𝑓: frequenza emessa dalla sorgente
Se la sorgente e l’osservatore si avvicinano si sceglie il segno + al numeratore e il segno – al denominatore
Se la sorgente e l’osservatore si allontanano sceglie il segno − al numeratore e il segno + al denominatore
Nel caso in cui la direzione non è la stessa la relazione che consente di determinare la variazione di frequenza percepita da un
osservatore in moto relativo rispetto alla sorgente è data da:
𝑓′ = 𝛾
𝑓
1±𝛽 ∙cos 𝜃 ′