POLITICA ECONOMICA I – Corso A-K – Anno Accademico 2009/2010
Prof. Mario Volpe
Esercitatore: Dr.ssa Alessia Bernardi
[email protected]
ESERCITAZIONE DEL 17/03/2010
Esercizio 1 – Il mercato del lavoro
Supponi che le imprese fissino i prezzi con un mark-up pari al 10%. Supponi inoltre che la funzione
F(u,z), che spiega come i salari dipendono dal tasso di disoccupazione sia:
F(u,z)=1-u
dove u è il tasso di disoccupazione.
a) Determinare il salario reale di equilibrio
b) Determinare il tasso naturale di disoccupazione
SOLUZIONE
a) L’equazione dei prezzi è:
W/P = 1/(1 + µ)
per cui:
W/P = 1/(1 + 0.1) = 0.909
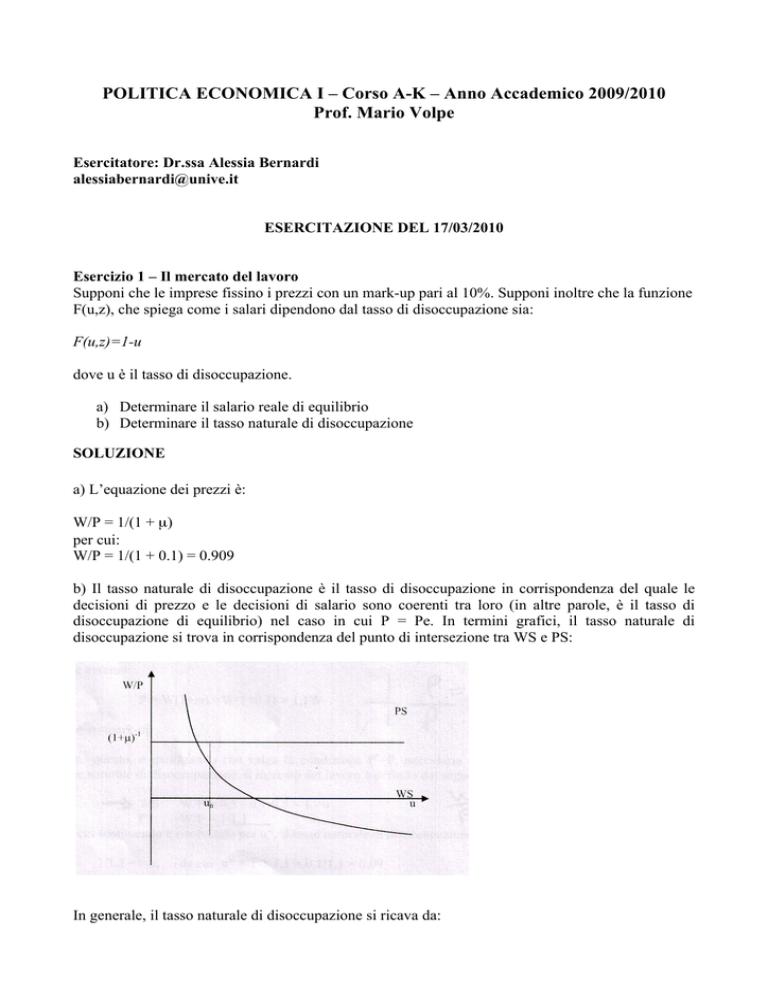
b) Il tasso naturale di disoccupazione è il tasso di disoccupazione in corrispondenza del quale le
decisioni di prezzo e le decisioni di salario sono coerenti tra loro (in altre parole, è il tasso di
disoccupazione di equilibrio) nel caso in cui P = Pe. In termini grafici, il tasso naturale di
disoccupazione si trova in corrispondenza del punto di intersezione tra WS e PS:
In generale, il tasso naturale di disoccupazione si ricava da:
1
1+ µ
F(u,z) = (1− u)
1
(1− un ) =
1+ µ
un = 1− 0,909 = 0,091
F(u,z) =
€
Esercizio 2 – Il mercato del lavoro
Supponete che in un dato sistema economico i salari siano determinati sulla base della seguente
funzione:
W = Pe(0,5 - u + z)
a) Se i sussidi alla disoccupazione sono tali per cui z=0,5 e se le imprese fissano i prezzi con un
mark-up del 10%, determinate il salario reale di equilibrio e il tasso di disoccupazione naturale di
questa economia. Si fornisca anche una rappresentazione grafica.
b) Supponete che si voglia ridurre il tasso di disoccupazione naturale al livello del 5%. Come
dovrebbe agire la legislazione antitrust per ottenere tale scopo?
SOLUZIONE
a) Per prima cosa dobbiamo definire formalmente l’equazione dei prezzi. In base alle ipotesi sopra
fatte avremo:
P = W(1+m) = W(1+0,1) = 1,1W
dove m=mark-up
Detto questo, e ipotizzando che valga la condizione Pe=P, necessaria quando si considera il tasso
naturale di disoccupazione, il mercato del lavoro Ë definito dal seguente sistema:
WS: W/P = 0,5 - u + 0,5 = 1 - u
PS:
W/P = 1/1,1
Per cui sostituendo e risolvendo per u*, il tasso naturale di disoccupazione, otteniamo,
1/1,1 =1-u;
da cui: u* = 1-1/1,1 = 0,1/1,1 = 0,09.
Il salario reale, W/P, è pari a 1/1,1.
Il grafico sottostante rappresenta l’equilibrio nel mercato del lavoro:
b) Per raggiungere un tasso di disoccupazione del 5%, u* = 0,05, abbiamo la possibilità di
fissare un adeguato tasso di mark-up, che può essere modificato dalla legislazione antitrust.
La soluzione si ottiene trovando quel valore di m che consente di risolvere il modello:
WS: W/P = 1 - u* = 1 - 0,05 = 0,95
PS:
W/P = 1/(1+m)
Per cui abbiamo:
0,95=1/(1+ m);
1+ m =1/0,95;
m *= 1,052-1=0,052
Esercizio 3 - Il modello AS-AD
Si assuma che l’economia stia operando al livello di produzione Yn .
Si supponga un aumento di G.
a) Facendo uso dello schema AS-AD, si illustri graficamente l’equilibrio iniziale mostrando
€
cosa succede alle curve come immediate conseguenza
della manovra.
b) Quali sono gli effetti di breve periodo di tale manovra su Y, P e i?
c) Quando Y > Yn cosa accade alla curva AS dell’anno succesivo?
d) Quali sono gli effetti di medio periodo dell’aumento di G?
€
SOLUZIONE
a) Il Governo decide di aumentare il disavanzo di bilancio. La curva AD si sposta in alto in
AD’: il livello di produzione di equilibrio è superiore al livello di produzione naturale e i
prezzi aumentano. Si mette in moto il meccanismo di aggiustamento (attraverso
l’adeguamento delle aspettative al prezzo) che provoca spostamenti della AS verso l’alto
fino al raggiungimento del nuovo equilibrio di medio periodo.
b) Gli effetti iniziali dell’aumento di G sono:
L’aumento della spesa pubblica sposta la curva di domanda aggregata verso destra: ad un dato
livello di prezzi la domanda di beni è ora superiore;
L’economia si sposta da A a B dove produzione e prezzi sono più alti;
L’effetto iniziale dell’aumento del disavanzo è pertanto un aumento di P, una riduzione dello stock
reale di moneta offerta M/P e un aumento del tasso di interesse i;
Gli effetti sull’investimento sono ambigui, perché aumentano sia la produzione che il tasso di
interesse.
c) Quando Y > Yn , al crescere del livello atteso dei prezzi la curva AS si sposta in alto. Allo
spostarsi della curva Y diminuisce, P aumenta, M/P diminuisce, i aumenta, I diminuisce.
d) Gli effetti di medio periodo di un aumento di G sono:
€ al suo livello naturale;
Y torna
P è permanentemente maggiore;
M/P è permanentemente minore;
i è permanentemente maggiore;
I è permanentemente minore;
l’aumento di G è esattamente compensato dalla riduzione di I.
ESERCITAZIONE DEL 23/03/2010 e del 25/03/2010
Esercizio 1 - Il mercato aperto
Si consideri un paese caratterizzato dalle seguenti equazioni:
C= 400 + 0,8 ( Y-T)
I = 200 – 12 i + 0,04 Y
G=1800
X= 0,05Y* + 200ε
IM = 0,01 Y - 5ε
ε=20
i=6 (punti non 6 per cento)
Y*=1000
Lo stato incassa imposte al netto delle pensioni e dei trasferimenti per un importo pari a -2000 più il
35% del PIL.
Si calcoli:
1) Il moltiplicatore della domanda, la spesa autonoma e il PIL
2) Il saldo commerciale e il saldo pubblico
Quest’ anno lo stato vuole aumentare le pensioni di 100 e ridurre la spesa per la ricerca di 200 e si
verifica un deprezzamento nominale, che si traduce in un apprezzamento reale: ε=15.
Si calcoli:
3) Il moltiplicatore della domanda, la spesa autonoma e il PIL
4) Il saldo commerciale e il saldo pubblico
Si illustri che in presenza di avanzi gemelli il paese può effettivamente esportare risparmio.
SOLUZIONE
Notazione:
in questo esercizio ε = EP*/P = prezzo relativo dei beni stranieri in termini di beni nazionali.
Quando ε DIMINUISCE , vuol dire che i beni stranieri relativamente a quelli nazionali sono
piu’ economici e quindi le esportazioni DIMINIUSCONO e le importazioni AUMENTANO.
Per questo X è una funzione positiva di ε e IM è una funzione negativa di ε (contrariamente al
testo, il quale assume ε = EP/P* ).
Calcoliamo il moltiplicatore, la spesa autonoma e il PIL in generale.
C=Co +C1(Y-T)
T=To + T1Y
I=Io + I1Y – ni
X= AY* + B ε
IM = C Y – Dε
Equilibrio nel mercato dei beni:
Y= Z
Y= Co +C1(Y-( To + T1Y))+ Io + I1Y – ni+ AY* + B ε - (C Y – Dε) ε + G
Y[ 1- C1 (1- T1) - I1 + Cε] = Co - C1 To + Io – ni + AY* + B ε + Dε ε + G
Moltiplicatore = 1 / [ 1- C1 (1- T1) - I1 + Cε]
Spesa autonoma = Co - C1 To + Io – ni + AY* + B ε + Dε* ε + G
PIL = 1 / [ 1- C1 (1- T1) - I1 + Cε]* (Co - C1 To + Io – ni + AY* + B ε + Dε ε + G )
Notazione:
α= 1- C1 (1- T1) - I1 + Cε
β= Co - C1 To + Io + AY* + B ε + Dε ε + G
e quindi
Moltiplicatore = 1 / α
Spesa autonoma = β – ni
1) 1 / [ 1- C1 (1- T1) - I1 + Cε] = 1/ [ 1-0,8(1-0,35) – 0.04 + 0,01(20) ] = 1/[1-0,52 -0,04
+0,2]=1/0,64=1,563
SA = 400 – 0,8(-2000) + 200 -12*6+ 0,05(1000) + 200(20)+5*20*20 + 1800 = 9978
Y = 9978 * 1,563 = 15595
2) T = -2000 + 0.35 (15595) = 3458
G – T = 1800 – 3458 = -1658 (avanzo, G < T)
X – εIM = 0,05 (1000) + 200 (20) – 20( 0,01 (15595) – 5(20)) = 4050 – 20(155,95 – 100) = 2931
(avanzo commerciale)
3) G = 1600; T= -2100 + 0,35 Y; Ε=15
m= 1 / [ 1- C1 (1- T1) - I1 + Cε] = 1/ [ 1-0,8(1-0,35) – 0.04 + 0,01(15) ] = 1/0,59 = 1,695
SA = SA = 400 – 0,8(-2100) + 200 -12*6+ 0,05(1000) + 200(15)+5*15*15 + 1600 = 7983
Y = m *SA = 1,695 * 7983 = 13531
4) T = -2100 + 0,35 (13531) = 2635,85
G – T = 1600 – 2635,85 = - 1035,85 ( peggiorato)
X – εIM = 0,05 (1000) + 200 (15) – 15( 0,01 (13531) – 5(15)) = 3050 – 15(135,31 – 75) = 3050904,65= 2146 (peggiorato)
NX = X – εIM = S + (T-G) - I
NX > 0 => S + (T-G) - I > 0 => S + (T-G) > I
Il risparmio privato e pubblico eccedono gli investimenti: per cui questo paese è un creditore netto.
Esercizio 2 - Il mercato aperto nel modello IS-LM
C = 300 + 0,4 (Y-T)
I = 300 – 20i + 0,1 Y
X= 0,1Y* + 100 ε
IM = 0,2 Y - 200 ε
G= 800
T= 600
Y*=1200
ε = EP*/P = 1.2
LM : i = -30 +0,05Y
1) Si determini l’equilibrio IS-LM (Y, i)
2) Si calcoli l’avanzo commerciale
3) Si analizzino gli effetti di un apprezzamento (ε =1) su Y, i, e l’avanzo commerciale
d’equilibrio
SOLUZIONE
1) La domanda di beni nazionali è data da:
ZZ = C + I + G + X - IM ε
Troviamo la IS imponendo la condizione d’equilibrio: Y= ZZ
Y = 300 + 0,4 (Y-T) + 300 – 20i + 0,1 Y + 800 +0,1Y* + 100 ε – [0,2 Y - 200 ε] ε
Y = 300 + 0,4 Y- 0,4 600 + 300 – 20i + 0,1 Y + 800 +0,1 (1200) + 100 (1,2) – 0,2 Y(1,2) + 200
(1,2)(1,2)
Y[ 1- 0,4 -0,1 + 0,2(1,2) ] = 1688 – 20i
α = 1- C1 (1-T1) – n + B (ε) = 1- 0,4 -0,1 + 0,2(1,2) = 0,74
β= Co + Io + G – ToC1 + A Y* + Bε +Dεε = 300 + 300 + 800– 0,4(600) +0,1 (1200) + 100 (1,2) +
200 (1,2)(1,2) = 1688
IS: i = β /20 – α /20 Y
IS: i = 1688/20 – 0,74/20 Y
Equilibrio: risolviamo il sistema IS-LM
LM : i = -30 +0,05Y
IS: i = 1688/20 – 0,74/20 Y
=> -30 +0,05Y = 1688/20 – 0,74/20 Y
=> Y* = 114,1/0,087 = 1315 i*= -30 + 0,05(1315)=35,7
2) NX = X – IM ε = 0,1Y* + 100 ε – [0,2 Y - 200 ε ]ε = 0,1 (1200) +1,2(100) – [0,2(1315) –
200(1,2)]1,2 = 240 – 27,6 = 212,4
3)
E= numero di euro per 1 dollaro
E ↓, apprezzamento : servono meno unità di moneta nazionale per 1 unità di moneta estera.
Prezzi esteri in moneta nazionale si riducono
X= 0,1Y* + 100 ε ↓
IM = 0,2 Y - 200 ε ↑
α = 1- C1 (1-T1) – n + B (ε) = 1- 0,4 -0,1 + 0,2(1) = 0,7 => pendenza IS si riduce
β= Co + Io + G – ToC1 + A Y* + Bε +Dεε = 300 + 300 + 800– 0,4(600) +0,1 (1200) + 100 (1) +
200 (1)(1) = 1580 => IS si abbassa
Nuovo equilibrio:
IS: i = 1580/20 – 0,70/20 Y = 79 – 0,035Y
LM : i = -30 +0,05Y
=> 79 – 0,035Y=-30 +0,05Y == > Y* = 109/0,085 = 1282
i*= -30 + 0,05 (1282) = 34
NX = X – IM ε = 0,1Y* + 100 ε – [0,2 Y - 200 ε ]ε = 0,1 (1200) +1(100) – [0,2(1282) – 200(1)]1 =
220 – 56,4 = 163,6
Un apprezzamento reale : riduce Y, i (perchè si riduce la domanda di moneta) e l’avanzo
commerciale peggiora. La ZZ e la curva NX si abbassano.
Esercizio 3 - Il mercato aperto
Supponete che un paese area euro sia in DISAVANZO COMMERCIALE e il governo voglia
eliminarlo. Analizzate l’efficacia delle seguenti politiche
a) Politica fiscale interna;
b) Politica di cambio;
c) Coordinamento con i governi stranieri.
d) Potete concludere che le politiche b e c sono identiche e che in assenza di coordinamento
possiamo sostituire c con b?
SOLUZIONE
a) NX = X (Y*, ε) – IM(Y, ε) ε
Per migliorare la bilancia commerciale il governo deve indurre una riduzione di Y, che a sua
volta ridurrà le importazioni. Per fare questo esso può ridurre G o aumentare T: tale stretta
fiscale ridurrà la produzione via moltiplicatore, quindi il reddito disponibile, quindi la domanda
di tutti i beni, fra i quali anche quelli esteri.
Tale politica abbassa la curva ZZ’ senza modificare la NX.
b) Se vale la condizione di Marshall-Lerner, la politica di cambio che elimina il disavanzo è un
DEPREZZAMENTO della valuta nazionale (P/EP* ↓ ) .
Indichiamo il deprezzamento come E↑ ( E = n° di unità di moneta nazionale per una unità
di moneta estera aumenta ) e quindi ε ↑
Di nuovo ε = EP*/P = prezzo dei beni esteri relativo ai beni nazionali. Se aumenta i beni
nazionali sono più competitivi, quindi:
le esportazioni aumentano, le importazioni diminuiscono e la bilancia commerciale migliora.
Inoltre anche Y aumenta.
c) Un coordinamento con i governi stranieri capace di indurre un aumento di Y*, attraverso un
aumento di G* o T*, aumenterebbe solo X. Questo effetto poi indurrebbe un aumento di Y.
Riassumiamo gli effetti di queste politiche con una tabella:
POLITICA FISCALE
INTERNA
POLITICA DI CAMBIO
POLITICA ESTERA –
COORDINAMENTO
NX
↑
Y
↓
↑
↑
↑
↑
d) Nonostante le politiche b e c abbiano gli stessi effetti su NX e Y, esse non sono del tutto
identiche perchè la politica di cambio ha un ulteriore effetto negativo sui consumatori nazionali,
che devono pagare prezzi più alti per i beni esteri.