Compit recupero eletrotecnica classe terza
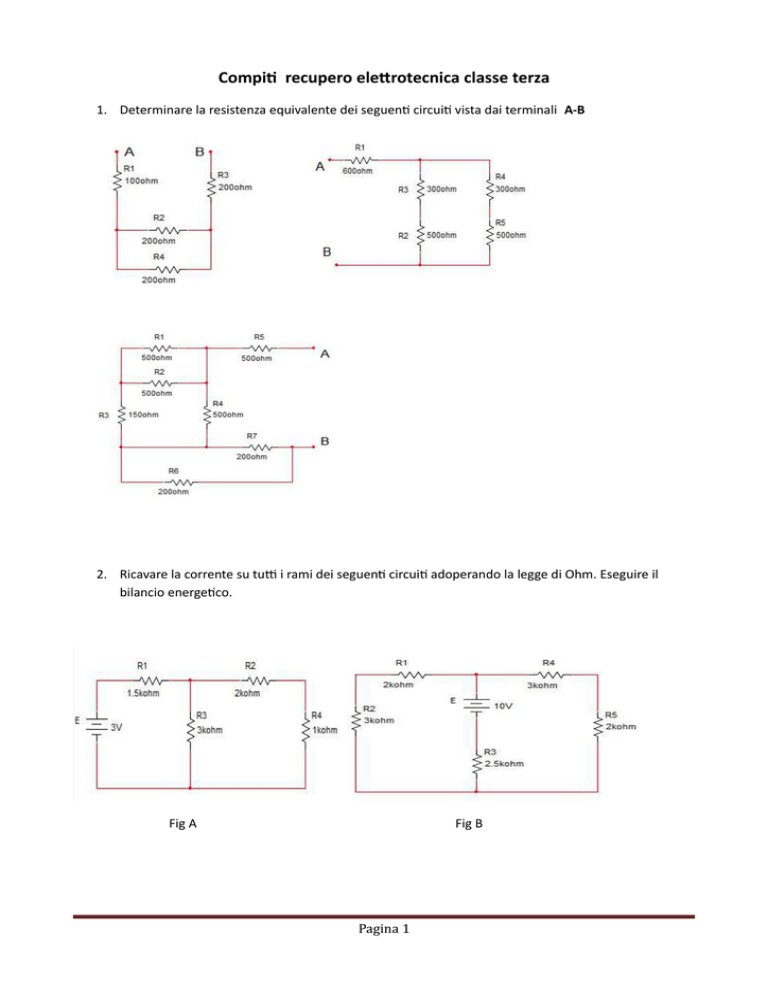
1. Determinare la resistenza equivalente dei seguent circuit vista dai terminali A-B
2. Ricavare la corrente su tut i rami dei seguent circuit adoperando la legge di Ohm. Eseguire il
bilancio energetco.
Fig A
Fig B
Pagina 1
Fig C
3. Ripetere gli esercizi di fg A e Fig B utlizzando i principi di Kirchhof
4. Ricavare le corrent in tut i rami adoperando il principio di sovrapposizione degli efet
Fig D
Fig E
Fig F
Pagina 2
5. Ripetere gli esercizi di fg D, Fig E e Fig F adoperando i principi di Kirchhof
6. Per l circuit di fgura C e D calcolare la corrente sul ramo contenente R4 adoperando il principio di
Thevenin
7. Ricavare la corrente sul ramo contenente Ra applicando il principio di Thevenin
Fig G
8. Ripetere l’esercizio di fgura G adoperando i principi di Kirchof.
9. Rifare tut gli esercizi eseguit in classe
Pagina 3
Compit recupero eletronica classe terza
1. Scrivi la funzione canonica relatva alle seguent tabelle di verità; minimizza poi tali funzioni utlizzando i
teoremi dell’algebra di Boole
A
0
0
0
0
0
0
0
0
1
1
1
1
1
1
1
1
B
0
0
0
0
1
1
1
1
0
0
0
0
1
1
1
1
C
0
0
1
1
0
0
1
1
0
0
1
1
0
0
1
1
D
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
Y
1
1
0
0
0
1
1
1
1
1
0
1
0
0
0
1
A
0
0
0
0
0
0
0
0
1
1
1
1
1
1
1
1
B
0
0
0
0
1
1
1
1
0
0
0
0
1
1
1
1
C
0
0
1
1
0
0
1
1
0
0
1
1
0
0
1
1
D
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
Y
1
1
1
0
0
0
1
0
1
0
0
1
1
0
0
1
A
0
0
0
0
0
0
0
0
1
1
1
1
1
1
1
1
B
0
0
0
0
1
1
1
1
0
0
0
0
1
1
1
1
C
0
0
1
1
0
0
1
1
0
0
1
1
0
0
1
1
D
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
Y
0
0
1
0
1
1
1
0
1
0
1
1
1
0
1
1
2. Trasforma le funzioni minime otenute nell’esercizio precedente in sole porte Nand a due ingressi
3. Minimizza le seguent funzioni usando tut i teoremi necessari:
Y = ( A + B )( A +B C ) + Ā B̄+ Ā C̄
Y = A B ( C +B ) + A B C̄ + A B̄
Y = Ā ( B +C ) + A B C̄ + A B+ C
Y = ( A + B̄+C )( A+ B̄+ C̄ ) ( Ā +C)
Y = A B C+ { A B ⌈ D+ Ā ( C̄ D+ B ) + B̄ D ⌉+ A B̄ }+ A B̄ C̄
4. Esegui gli esercizi del punto 1 adoperando le mappe di Karnaugh. Disegna i relatvi circuit.
Pagina 4
5. Minimizza le seguent tabelle utlizzando le mappe
A
0
0
0
0
0
0
0
0
1
1
1
1
1
1
1
1
B
0
0
0
0
1
1
1
1
0
0
0
0
1
1
1
1
C
0
0
1
1
0
0
1
1
0
0
1
1
0
0
1
1
D
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
Y
0
0
X
0
0
1
1
X
1
X
0
0
X
1
X
1
A
0
0
0
0
0
0
0
0
1
1
1
1
1
1
1
1
B
0
0
0
0
1
1
1
1
0
0
0
0
1
1
1
1
C
0
0
1
1
0
0
1
1
0
0
1
1
0
0
1
1
D
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
Y
1
X
X
0
1
0
X
X
0
1
1
X
1
X
0
1
A
0
0
0
0
0
0
0
0
1
1
1
1
1
1
1
1
B
0
0
0
0
1
1
1
1
0
0
0
0
1
1
1
1
C
0
0
1
1
0
0
1
1
0
0
1
1
0
0
1
1
D
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
Y
0
X
1
1
X
X
0
1
0
X
X
1
1
1
X
1
6. Esegui gli esercizi dei punto 1 e 5 adoperando per ciascuno mux del tpo 8/1. Disegna i circuit relatvi.
7. Progeta una rete logica in grado di eseguire la seguente espressione:
y=3 A−2 B+2
Dove A e B sono due numeri binari di due bit ciascuno. La rete deve fornire anche il segno dell’espressione.
Eseguire il progeto sia mediante porte logiche che mediante mux.
8. Progeta e disegna i seguent contatori asincroni con le relatve specifche:
3÷9
F.F PET ingressi asincroni atvi alt
12÷6
F.F NET ingressi asincroni atvi alt
9÷3
F.F PET ingressi asincroni atvi alt
6÷12
F.F PET ingressi asincroni atvi bassi
2÷13
F.F NET ingressi asincroni atvi bassi
8÷1
F.F PET ingressi asincroni atvi alt
3÷9
F.F NET ingressi asincroni atvi alt
Pagina 5










