cap 4

4. Sorgenti di Rumore Elettromagnetico ed
Ottico
4.1 Luce e Rumore
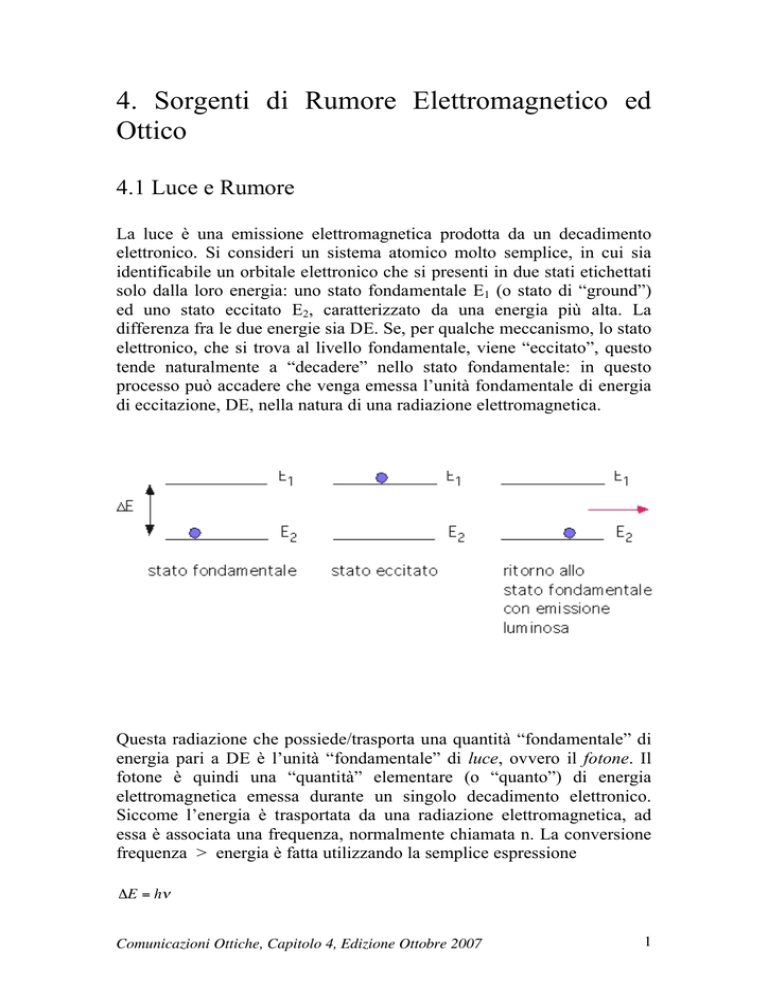
La luce è una emissione elettromagnetica prodotta da un decadimento
elettronico. Si consideri un sistema atomico molto semplice, in cui sia
identificabile un orbitale elettronico che si presenti in due stati etichettati
solo dalla loro energia: uno stato fondamentale E1 (o stato di “ground”)
ed uno stato eccitato E2, caratterizzato da una energia più alta. La
differenza fra le due energie sia DE. Se, per qualche meccanismo, lo stato
elettronico, che si trova al livello fondamentale, viene “eccitato”, questo
tende naturalmente a “decadere” nello stato fondamentale: in questo
processo può accadere che venga emessa l’unità fondamentale di energia
di eccitazione, DE, nella natura di una radiazione elettromagnetica.
Questa radiazione che possiede/trasporta una quantità “fondamentale” di
energia pari a DE è l’unità “fondamentale” di luce, ovvero il fotone. Il
fotone è quindi una “quantità” elementare (o “quanto”) di energia
elettromagnetica emessa durante un singolo decadimento elettronico.
Siccome l’energia è trasportata da una radiazione elettromagnetica, ad
essa è associata una frequenza, normalmente chiamata n. La conversione
frequenza > energia è fatta utilizzando la semplice espressione
"E = h#
!
Comunicazioni Ottiche, Capitolo 4, Edizione Ottobre 2007
1
dove h è una costante di proporzionalità chiamata costante di Planck che
vale 6.6624 10-34 Joule Hz.
La modellizzazione del fenomeno sopra-descritto di emissione luminosa
ha impegnato i fisici per più di mezzo secolo ed ha portato alla
consapevolezza che i modelli “classici” elettromagnetici non potevano
dare ragione compiuta dello stesso: la soluzione del problema della
emissione luminosa, e quindi della natura della luce, trova il suo
compimento solo con l’introduzione della meccanica quantistica ( che
viene formalizzata nel 1930 con la pubblicazione del libro “I principi
della meccanica quantistica” di P.A.M. Dirac ). Essa prevede che il modo
più efficace di modellizzare il semplice sistema sopra-descritto sia quello
di immaginarlo come un oscillatore armonico, ovvero un sistema che
conserva la sua energia e che la trasforma in continuazione da energia
potenziale a energia cinetica con una velocità di “scambio” che viene a
coincidere con la frequenza n della emissione luminosa stessa.
L’introduzione di questo modello rende inutile approfondire il
meccanismo elettromagnetico-atomico di questo fenomeno, comunque
non classicamente spiegabile, e lo riporta a modelli astratti del tipo
massa-molla o induttore-capacitore. Questi modelli sono quindi “risolti”
con le tecniche della meccanica quantistica e della meccanica statistica e
la loro soluzione produce i valori aspettati di energia luminosa ed anche
la descrizione più corretta della luce e delle sorgenti luminose. Questi
modelli rappresentano quindi la trattazione più rigorosa dei problemi di
emissione ed assorbimento della luce: normalmente, siccome i due
modelli sono equivalenti, si preferisce fare riferimento al modello massamolla piuttosto che a quello induttore-capacitore. Per il primo, chiamando
q la coordinata della massa m e k la costante di molla, la somma della
Comunicazioni Ottiche, Capitolo 4, Edizione Ottobre 2007
2
energia potenziale (quella accumulata dalla molla) e della energia cinetica
vale
Kq 2 p 2
Etotale =
+
2
2m
!
dove p rappresenta la quantità di moto. Dalla relazione classica che lega
la frequenza di oscillazione del sistema n ai parametri k ed m
" = 2#$ =
k
m
si ottiene l’equazione fondamentale che
dell’oscillatore armonico alle quantità p e q,
!
E totale =
!
lega
l’energia
totale
1 2 2
(" q + p2 )
2
Questa equazione è molto importante perché le tre quantità E, q e p
possiedono una descrizione equivalente in meccanica quantistica (sono
cioè “misurabili” in senso stretto): la loro trasposizione nel formalismo
della meccanica quantistica genera quindi una equazione agli autovalori
le cui soluzioni sono i livelli quantizzati di energia che l’oscillatore
armonico può possedere e le cui autosoluzioni sono i modi di oscillazione
dello stesso. In particolare si ottiene che i livelli di energia che
l’oscillatore armonico può possedere sono discreti (quantizzati) secondo
l’espressione:
"
1%
E totale = $ n + ' h(
#
2&
!
come appaiono anche nella figura seguente.
L’introduzione del concetto di “oscillatore armonico” è fondamentale in
tutte le descrizioni dei fenomeni luminosi e permette di ricavare le
proprietà di tutte le sorgenti di luce conosciute ed anche del “rumore”
luminoso. Nelle comunicazioni ottiche si ha a che fare con tre tipi di
”luce”: la “luce segnale” che è tipicamente una sorgente laser; la “luce
termica” naturale che è assunta a “rumore ambientale” e la “luce termica”
originata da emissione spontanea che caratterizza il rumore degli
amplificatori ottici.
Conoscere le caratteristiche delle diverse “luci” segnale e rumore che
concorrono allo studio del sistema di comunicazioni ottiche è molto
importante al fine di stabilire i limiti di funzionamento del sistema stesso,
la corretta valutazione del rapporto segnale/rumore, la valutazione della
Comunicazioni Ottiche, Capitolo 4, Edizione Ottobre 2007
3
qualità della trasmissione, il tipo di sorgenti di rumore, ecc.
Esse possono essere descritte sulla base di tre parametri misurabili:
- la modalità temporale
- la modalità spaziale
- la statistica di insieme
Modalità temporale. Un oscillatore armonico è caratterizzato da una sola
frequenza di oscillazione: esso presenta quindi solo un modo temporale
ed il suo spettro è strettamente mono-modale. La luce su un solo modo
temporale è quindi monocromatica. Questa è la caratteristica più tipica
della luce laser. Possono esserci emissioni luminose che coinvolgono
insiemi di oscillatori armonici di diversa frequenza di oscillazione, in
questo caso ottengo luce con spettro ampio, discreto o continuo. Questa è
la caratteristica tipica della luce delle lampade o luce termica, ma anche
sorgenti laser possono avere spettri ampi. La modalità temporale della
luce è quindi legata alle sue caratteristiche di purezza spettrale.
Modalità spaziale. La radiazione elettromagnetica è per sua natura
propagante ed in quanto tale è quindi caratterizzata da un vettore d’onda
k=
!
2"
#
Il vettore k occupa uno spazio tre-dimensionale e quindi per ogni
frequenza n vi possono essere una molteplicità di modi spaziali, ognuno
dei quali etichettato da un diverso valore di k. In uno spazio illimitato di
propagazione omogeneo ed isotropo, questi modi occupano la superficie
di una sfera di raggio |k|: tutte le direzioni ed i versi sono permessi e per
uno stessa frequenza sono permesse infinite realizzazioni spazio-modali.
Questo non è vero in uno spazio limitato (ad esempio di lunghezza L) ed
Comunicazioni Ottiche, Capitolo 4, Edizione Ottobre 2007
4
anisotropo. In questo caso i “modi” sono autosoluzioni discrete della
coordinata spaziale, in altri termini il vettore d’onda non può assumere
qualsiasi lunghezza ma il suo modulo deve essere un multiplo del vettore
d’onda più piccolo, questo essendo p/L. Se poi lo spazio è anisotropo (
come ad esempio succede per le lunghezze d’onda ottiche in un mesacristallo o photonic-band-gap material) alcune direzioni spaziali sono
proibite o risulta una densità di modi variabile a seconda della frequenza
considerata.
Può essere utile stimare quanti modi spaziali vi siano in un intervallo di
vettori d’onda assegnato dk e nel corrispondente intervallo di pulsazioni
dw. Immaginiamo che la radiazione sia contenuta in un cubo di lato L. I
“modi” (cioè le realizzazioni stazionarie del campo) si adageranno nella
scatola come onde sinusoidali i cui nodi coincideranno con le pareti:
quindi la massima lunghezza d’onda ospitata nella scatola sarà 2L ed il
massimo vettore d’onda sarà:
kM =
!
2" "
=
2L L
Se consideriamo uno spazio omogeneo ed isotropo quale spazio di
propagazione della luce, i modi occuperanno una corteccia di un
quadrante di sfera di raggio k spessa dk e cioè
1
4 "k 2 dk )
(
8
in questa corteccia di sfera vi saranno quindi
!
!
1
(4"k 2dk )
8
2
# " &3
% (
$L'
modi spaziali (il fattore 2 in alcune trattazioni si omette: esso in questa
trattazione tiene conto dei due stati di polarizzazione che ciascun modo
può possedere). Il numero di modi per unità di volume nell’intervallo dk
definisce la densità di modi rkdk e vale quindi
" k dk = k 2 dk / # 2
ovvero in termine di frequenza
!
!
"# d# = # 2 d$ / % 2c 3
Comunicazioni Ottiche, Capitolo 4, Edizione Ottobre 2007
5
Le comunicazioni ottiche prevedono normalmente l’impiego di luce
monomodale, perché la propagazione che si considera è solitamente
quella in fibre ottiche monomodali ed anche le sorgenti laser vengono
spazialmente filtrate per renderle monomodali. La luce ambiente e molta
luce considerata “rumore” si presenta naturalmente multimodale.
Se si considerano solo i parametri modi temporali e modi spaziali il
quadro complessivo delle diverse “luci” possibili si presenta come nello
specchietto seguente
Comunicazioni Ottiche, Capitolo 4, Edizione Ottobre 2007
6
Statistica di insieme. Le collezioni di oscillatori armonici elementari che
costituiscono le sorgenti luminose si possono presentare con diverso
grado di energia di eccitazione: si dice in altri termini che gli stati degli
oscillatori armonici sono diversamente occupati, il numero di
occupazione essendo il numero n di fotoni che occupa lo stato. La
distribuzione di energia di eccitazione (ovvero dell’n) dell’insieme di
oscillatori armonici della sorgente luminosa genera delle statistiche che
caratterizzano in modo particolare i diversi tipi di sorgenti luminose. In
particolare, si può dimostrare che la luce di origine termica è
caratterizzata da una distribuzione di Bose-Einstein (questo tipo di
statistica è quello che caratterizza la luce detta anche “caotica”, che
rappresenta la luce “rumore” tipica dei sistemi di comunicazione ottica)
mentre la luce ottenuta con una inversione dell’equilibrio termodinamico,
la luce laser, presenta una distribuzione di Poisson (questo tipo di
statistica è quello che caratterizza la luce detta anche “ordinata” , che
rappresenta la luce “segnale” tipica dei sistemi di comunicazione ottica) .
Se si considerano solo i parametri statistica di insieme e modi spaziali il
quadro complessivo delle diverse “luci” possibili si presenta come nello
specchietto seguente
Comunicazioni Ottiche, Capitolo 4, Edizione Ottobre 2007
7
4.2 La funzione di Planck
Che tipo di “rumore” influenza i sistemi di comunicazione ottica? Se
consideriamo i segnali ottici un particolare tipo di segnali
elettromagnetici, questa domanda è riportabile alla più generale domanda:
che tipo di rumore elettromagnetico influenza i sistemi di comunicazione
? la trattazione del “rumore” è di fondamentale importanza per tutti i
sistemi di comunicazione (sia alle frequenze radio che alle frequenze
delle micro-onde) perché in ultima analisi quello che l’ingegnere delle
comunicazioni deve affrontare è sempre un problema di segnale/rumore:
deve quindi conoscere da dove proviene e che di natura è il rumore che
compete al suo sistema. La trattazione del rumore elettromagnetico più
condivisa considera una situazione di emissione elettromagnetica
proveniente da un insieme di oscillatori armonici contenuti in un bagno
termico, cioè in equilibrio termico con l’ambiente circostante
caratterizzato solo dalla sua temperatura. La presenza di energia termica
eccita e dis-eccita gli oscillatori armonici secondo leggi generali di
assorbimento ed emissione che vedremo più avanti nella trattazione. (vedi
figura)
Questa continua eccitazione e dis-ecittazione produce una radiazione
Comunicazioni Ottiche, Capitolo 4, Edizione Ottobre 2007
8
elettromagnetica nel mio contenitore (che supponiamo isolato rispetto
all’ambiente esterno e per questo chiamiamo “corpo nero”) che va
all’equilibrio con gli stati degli oscillatori locali. La domanda che ci
poniamo è : qual è il livello spettrale medio ( in W/Hz) che investe il mio
ricevitore elettromagnetico/ottico quando esso è posto in un ambiente a
temperatura T ? In altri termini, qual è l’energia elettromagnetica che
investe il mio ricevitore ? occorre intanto chiarire che non esiste la
possibilità di “isolare” il mio ricevitore dall’ambiente elettromagnetico
che origina il rumore perchè il ricevitore è “immerso” in un ambiente
caldo dotato di oscillatori armonici (gli stati elettronici della materia) e
quindi è illusorio pensare di potersi isolare da questa fonte primaria di
rumore. Inoltre il ricevitore dispone sempre di una “antenna” per ricevere
il segnale e da questa “antenna entra inevitabilmente anche il “rumore”
esterno che si trova alle stesse frequenze del segnale.
Per rispondere a questa domanda occorre “semplificare” il problema,
considerare cioè solo un sotto-insieme dei parametri che caratterizzano la
emissione elettromagnetica che, in generale, abbiamo visto essere
multimodale spaziale e temporale. Consideriamo ad esempio una
situazione monomodale sia spaziale che temporale. Il problema si
affronta ipotizzando che gli elementi emettitori di radiazione
elettromagnetica sino alle frequenze ottiche siano una collezione di
oscillatori armonici tutti uguali posti in un ambiente “caldo” per un tempo
sufficientemente lungo per essere considerati in uno stato stazionario.
Comunicazioni Ottiche, Capitolo 4, Edizione Ottobre 2007
9
L’agitazione termica degli oscillatori porta pian piano ad un equilibrio fra
la radiazione emessa e quella assorbita dagli stessi ed, all’equilibrio, la
probabilità di trovarli alla energia E n va come il fattore di Boltzmann
pn = e"E n / kT / # e"E n / kT
n
!
!
dove k è la costante di Boltzmann = 1.3810 "23 JK "1, T la temperatura
assoluta ed En
E n = ( n + 1/2) h"
!
!
Se faccio per il momeno l’approssimazione di trascurare il termine 1/2
(per facilitare il calcolo), e quindi di lavorare nell’ipotesi E n = nh"
siccome deve anche essere
"p
n
"e
=1
#nh$ / kT
!
=
n
1
1# e
#h$ / kT
e quindi
!
!
pn = e"nh# / kT [1" e"h# / kT ]
Conoscendo pn posso valutare il valore medio di n (ovvero n o “valore
di aspettazione” di n) ovvero quanti oscillatori armonici sono eccitati alla
energia En
!
!
n = " n pn =
!
%
(
"nh# / kT
"h# / kT
'$ ne
*(1" e
)
&n
)
% +
(
,
/
+
1
='
e"nh# / kT *(1" e"h# / kT ) =
1" e"h# / kT )
.
$
h# / kT 1(
0
+
h
#
/kT
+
h
#
/kT
1"
e
&
)
n
=
e"h# / kT
(1" e
"h# / kT
)
"h# / kT
)=
2 (1" e
e"h# / kT
1" e"h# / kT
!
Comunicazioni Ottiche, Capitolo 4, Edizione Ottobre 2007
10
e quindi moltiplicando sopra e sotto per e h" / kT ottengo che
n =
!
1
e
h" / kT
#1
!
Questa funzione è chiamata Funzione di Planck o anche Fattore BoseEinstein ed è molto importante in tutta la teoria elettromagnetica. Essa è
riportata in figura.
Esso ci dice in modo sintetico che per temperature “ambiente” dove
l’ascissa ha un valore molto alto, la probabilità di trovare oscillatori
armonici di alta frequenza eccitati tende a zero. Ad esempio, tipicamente
ho che a 23 °C
kT = 1,3810"23 • 296 = 408,410"23 joule
!
equivalente a 255 10-4 eV ovvero circa 25 meV.
Alle lunghezzed ‘onda tipiche delle comunicazioni ottiche, dove h" è
dell’ordine di 0,8 eV, significa che l’ascissa vale 32 ed n è pari a circa
1,26 10-14. Questo risultato non appare tale a frequenze non-ottiche, ad
esempio alle frequenze delle micro-onde, dove invece la !
radiazione di
“corpo nero” è ben presente: alle lunghezze d’onda
delle micro-onde la
!
Comunicazioni Ottiche, Capitolo 4, Edizione Ottobre 2007
11
probabilità di occupazione degli stati risulta dell’ordine di 102/103. Nella
tabella sottostante sono riportati i valori di n alle diverse lunghezze
d’onda delle telecomunicazioni.
E’ importante ricordare cosa rappresenta
! n . Esso
- è il numero medio di oscillatori armonici elementari eccitati:
secondo questa visione esso
! è il numero medio di fotoni che trovo
nel mio “contenitore” alla temperatura T o il numero medio di
fotoni che popola il mio campo elettromagnetico quantizzato:
questa è una visione corpuscolare della luce;
- sommato ad ½ e moltiplicato per h" rappresenta l’energia a cui si
porta l’oscillatore armonico eccitato dalla temperatura T: questa è
una visione ondulatoria della luce.
!
Le due visioni coesistono in tutta la trattazione rigorosa della luce.
Comunicazioni Ottiche, Capitolo 4, Edizione Ottobre 2007
12
Valutiamo ora quanto è la varianza di n , cioè (Dn)2. Debbo ricavare
n2
!
! )
&
n 2 = # "n n 2 = (1$ e$h% / kT )'# n 2e nh% / kT *
(n
+
n
& ,2
)
= (1$ e$h% / kT )' 2
e$nh% / kT *
#
( , h% /kT n
+
e dopo una serie di passaggi algebrici ottengo che
!
n2 = n + 2 n
2
da cui
!
("n)
!
2
(
= n2 # n
2
)=
2
n +2 n # n
2
= n + n
2
cioè le fluttuazioni di n sono sempre più grandi del suo valore medio:
questo ci autorizza a considerare nelle comunicazioni ottiche l’emissione
di corpo nero come “rumore”.
!
Dalla conoscenza del numero di fotoni eccitati alla temperatura T, n , si
può ricavare una utile espressione della distribuzione di probabilità pn.
Infatti essendo
n =
1
!
e h" / kT #1
si ottiene che
!
(e
h" / kT
#1) n = 1
da cui
!
e h" / kT n # n = 1
e h" / kT =
!
1+ n
n
Comunicazioni Ottiche, Capitolo 4, Edizione Ottobre 2007
13
e quindi
e"h# / kT =
n
1+ n
e quindi siccome per definizione
!
pn = e"nh# / kT (1" e"h# / kT )
sostituendo termine a termine ottengo
!
" n %n "
n % n
pn = $
' $1(
'=
#1+ n & # 1+ n &
pn =
!
n
(n
n
(1+ n ( n )
n +1
( n + 1)
n
+ 1)
n +1
Questa distribuzione di probabilità pn in funzione del valor medio di n, è
molto importante, ricorre spesso nella trattazione del rumore in teoria
delle comunicazioni ed è conosciuta in diversi modi a secondo del
contesto in cui si ricava: Distribuzione di Probabilità di Planck oppure
Distribuzione Termica oppure Distribuzione Geometrica oppure
distribuzione di Bose-Einstein. Essa è la distribuzione di probabilità che
caratterizza la “luce rumore” o “luce caotica” ed è tipica delle “sorgenti
termiche”, sorgenti luminose cioè in cui l’emissione di luce è ottenuta per
riscaldamento. Tipiche di stribuzioni di Bose-Einstein sono riportate nella
figura successiva.
Comunicazioni Ottiche, Capitolo 4, Edizione Ottobre 2007
14
Comunicazioni Ottiche, Capitolo 4, Edizione Ottobre 2007
15
4.3 La sorgente luminosa di tipo termico
Se supponiamo ora che il “corpo nero” possa emettere la radiazione
elettromagnetica in esso contenuta (attraverso una apertura che non
perturba le condizioni di equilibrio raggiunte), la radiazione così emessa
alle lunghezze d’onda tipiche dell’ottica si chiamerà “luce termica”.
Questo tipo di luce è molto comune nell’ottica: è la luce di tutte le
sorgenti che emettono in quanto portate a temperatura alta. La lampadina,
così come quasi tutte le sorgenti luminose non-laser, sono chiamate
“termiche” per segnalare l’origine del meccanismo che porta alla
emissione luminosa: un meccanismo di riscaldamento. Altre sorgenti
termiche importanti per le comunicazioni ottiche sono il sole (che
condiziona le comunicazioni ottiche cosidette “wireless” che impiegano
cioè fasci laser in propagazione libera), la luce delle stelle (che
condizionano le comunicazioni ottiche astronomiche), la luce delle
lampade ad arco ed a scarica di gas incandescente (i “neon” e le lampade
di tipo alogeno) che condizionano le comunicazioni ottiche “indoor”
(cioè quelle che avvengono all’interno di una stanza come il protocollo
Comunicazioni Ottiche, Capitolo 4, Edizione Ottobre 2007
16
IrDE) ecc.
Che caratteristiche di intensità I avrà questa luce? Per ricavarlo facciamo
l’ipotesi che la sua intensità sia direttamente proporzionale al numero di
fotoni in equilibrio dentro la cavità, cioè
pI " pn
si avrà allora
!
pI " pn =
n
(n
n
+ 1)
n +1
1
=
n
n
(n
n +1
+ 1)
n +1
n +1
1 # n &
=
%
(
n $ n + 1'
eseguo ora un cambio di variabile ponendo n + 1 " n # ed ottengo
!
n
n
1 % n # $1(
1 %
1 (
pI " pn =
'
* =
'1$
*
n # $1 & n # )
n # $1 &
n# )
!
#
#
dalla relazione (1" x ) = 1" nx ottengo
n
!
!
1 %
'1$
(n #) $1 &
#! 1
1 %
n
= 1 %1" 1
n $
n
"
n# (
* ovvero per n " grandi
n# )
&
(
(
!
'
"x
e ricordando lo sviluppo in serie di e
!
pn =
1 n/ n
e
n
!
e conseguentemente
!
1 "
pI =
e
I
!
I
I
Questa espressione ci dice che se osserviamo la radiazione emessa da una
sorgente “termica”, posto I la sua intensità media, il valore più
probabile osservato è zero e l’andamento per le altre intensità va come un
esponenziale negativo. L’andamento nel tempo dell’intensità di questa
sorgente si presenterebbe
come in figura.
!
Comunicazioni Ottiche, Capitolo 4, Edizione Ottobre 2007
17
Comunicazioni Ottiche, Capitolo 4, Edizione Ottobre 2007
18
4.4 La densità spettrale di potenza del rumore
elettromagnetico ed ottico: la legge di Planck
Abbiamo già visto come i dispositivi per telecomunicazione siano sempre
immersi in un “rumore elettromagnetico” presente a qualsiasi frequenza
dello spettro: è la cosidetta “radiazione di fondo”, presente per il solo
fatto di operare a temperature diverse dallo zero assoluto. La cattura di
questo rumore e quindi la sua influenza sul funzionamento del ricevitore
dipende dalle caratteristiche dei dispositivi: dipoli, antenne, resistenze e
fotodiodi catturano comunque un rumore, anche se a frequenze dello
spettro diverso.
Comunicazioni Ottiche, Capitolo 4, Edizione Ottobre 2007
19
Vogliamo ora usare l’espressione di Planck per determinare il valore
della densità spettrale eletttromagnetica W(w) (in W/Hz m-2 ovvero J/m2)
che costituisce la sorgente di rumore per il mio ricevitore.
Ho che:
W (" ) =
numero di fotoni energia modi
•
•
modo
fotone metro 2
e quindi
!
W (" ) = n • h" •
"2
# 2c 2
che è conosciuta anche come legge di Planck. Questa legge, il cui
!
andamento in funzione del parametro
h"
è riportato nella successiva
kT
figura stabilisce quanto “rumore” mi debbo aspettare alle diverse
frequenze dello spettro elettromagnetico in funzione della sola
temperatura T del corpo nero. !E’ una delle leggi più importanti della
fisica conosciuta anche prima dello sviluppo della meccanica quantistica.
Comunicazioni Ottiche, Capitolo 4, Edizione Ottobre 2007
20
Abbiamo visto precedentemente che alle energie tipiche della luce ed alla
temperatura ambiente, il parametro considerato vale circa 32: dalla legge
di Planck emerge quindi che alle frequenze ottiche io non dovrei avere
assolutamente rumore di origine ottica che entra nel sistema di
comunicazione. Solo a temperature molto più alte la legge di Planck
prevede una emissione “ottica” dal corpo nero. Infatti se valuto per quali
valori di frequenza elettromagnetica ho il massimo della funzione
prefissato un certo valore di temperatura, ottengo la cosidetta legge di
Wien che stabilisce una relazione fra le lunghezze d’onda l a cui ho il
massimo della funzione di Planck e la temperatura stessa
"=
!
[m]
(questa espressione della legge di Wien è stata ricavata da una legge di
Planck espressa in funzione della lunghezza d’onda, non quella riportata
precedentemente). Secondo la legge di Wien, per avere fotoni alla " di
1.5 µm, debbo avere sorgenti con temperatura pari a
T=
!
2,897 #10$3
T
2,897 "10#3
= 1930°K
1,5 "10#6
!
L’andamento della legge di Planck in funzione della temperatura del
“corpo nero” ed in funzione delle lunghezze d’onda della radiazione
emessa è illustrato nelle seguenti figure. Come si osserva, più voglio
ottenere una composizione spettrale di “colori” alti (cioè colori che
tendono al blu-violetto) più debbo innalzare la temperatura della
sorgente: per questo motivo la temperatura T sino ad ora considerata
viene anche chiamata “temperatura di colore”. Il sole, sorgente di luce per
eccellenza, ha una temperatura di colore circa 5700 °K: a questa
temperatura la emissione elettromagnetica ha un suo massimo nel range
di frequenze del visibile. Le lampade incandescenti hanno di solito
temperature di colore più basee (dai 3000 ai 2000 K) ed il cielo azzurro è
caratterizzato da una temperatura equivalente di colore molto alta, sopra i
7000 °K (non perché sia così caldo ma perché solo le componenti
spettrali a frequenze alte si salvano, le lunghezze d’onda rosse essendo
rimosse per diffusione).
Comunicazioni Ottiche, Capitolo 4, Edizione Ottobre 2007
21
Comunicazioni Ottiche, Capitolo 4, Edizione Ottobre 2007
22
4.5 L’introduzione dello stato vuoto e la legge di CallenWelton
Il risultato al paragrafo precedente è sempre stato visto con sospetto dai
fisici ed ha costituito un esempio chiaro di come la fisica
elettromagnetica classica non potesse spiegare compiutamente la teoria
del fotone e del campo ottico. Abbiamo visto al primo paragrafo come
all’oscillatore armonico veniva attribuita l’ energia totale
"
1%
E totale = $ n + ' h(
#
2&
!
Il termine ½, trascurato nel ricavare la funzione e la legge di Planck, deve
essere ri-introdotto per dare ragione del “rumore” che si osserva
inevitabilmente alle frequenze ottiche. Esso rappresenta l’energia dello
stato vuoto ovvero l’energia posseduta dall’oscillatore armonico anche in
assenza di eccitazione, in condizione di quiete. Questa energia è una
fluttuazione ineliminabile del “campo ottico” (del campo cioè formato
dall’insieme dei fotoni che costituiscono la luce) sempre presente a
qualsiasi frequenza e quindi spettralmente piatta. La presenza dello stato
vuoto e della sua energia giocano un ruolo fondamentale in tutta la teoria
delle comunicazioni ottiche. E’ quindi
1
E stato vuoto = h"
2
e la precedente espressione della legge di Planck
!
W (" ) =
1
e h# / kT $1
• h" •
"2
% 2c 2
si dovrà ora scrivere
!
!
%
1
1(
"2
W (" ) = ' h# / kT
+ * • h" • 2 2
&e
$1 2 )
+ c
Questa espressione viene ulteriormente semplificata se supponiamo la
radiazione emessa dal “corpo nero” sia vista da un “ricevitore”
spazialmente monomodale, che osserva il “corpo nero” dalla più piccola
area di coerenza possibile, cioè " #2 /2 , e che osserva una sola
polarizzazione (cade quindi il fattore 2 precedentemente introdotto) la
Comunicazioni Ottiche, Capitolo !
4, Edizione Ottobre 2007
23
Densità Spettrale di Potenza Nob(n) (in Joule o W/Hz) in funzione della
frequenza n sarà allora
$
1
1'
Nob(" ) = & h" / kT
+ ) • h"
%e
#1 2 (
!
espressione proposta da Callen e Welton nel 1951. La potenza
elettromagnetica vista dal ricevitore nella banda Dn sarà quindi
%
1
1(
Pob = Nob(" )#" = ' h" / kT
+ * • h" • #"
&e
$1 2 )
e questa funzione è rappresentata nella figura seguente
!
Comunicazioni Ottiche, Capitolo 4, Edizione Ottobre 2007
24
A partire dalla espressione di Callen-Welton posso avere due situazioni
di rumore distinte (nella ipotesi di operare in condizioni di temperatura
ambiente e quindi con kT dell’ordine di 25 meV):
1) h" / kT << 1. Sto considerando cioè frequenze elettromagnetiche, non
ottiche, che interessano quindi i componenti elettrici ed in particolare le
resistenze di carico dei circuiti. L’espressione precedente diventerà
!
$ kT '
N ob (" ) # h" & ) # kT
% h" (
Questa espressione rappresenta l’energia media che “entra” nel mio
sistema attraverso la resistenza di carico RL , provocando una fluttuazione
2
("i) di corrente che introduce rumore elettronico nel segnale
fotorivelato.
!
!
!
2) h" / kT >> 1: Questo è il caso delle frequenze ottiche che, come si vede
dal precedente grafico, dominano con l’energia dello “stato vuoto” lo
spettro di potenza alle frequenze sopra i 1013 Hz. E’ allora
!
1
N ob (" ) # h"
2
!
Come si osserva, il rumore che entra nel ricevitore corrisponde
esattamente a quello originato dalla energia di stato vuoto: questo risulta
quindi essere il “rumore limite” del processo di fotorivelazione: è come
se un campo ottico a media zero ma varianza non nulla interagisse con il
campo segnale di arrivo provocando una “incertezza” inevitabile nella
distribuzione di probabilità dei fotoni: la “traccia” di questa “incertezza”
si trova in diversi fenomeni di interesse del sistema di comunicazione
ottica, ad esempio:
a) nel segnale fotoelettrico come spettro di potenza a banda piatta che
costituisce lo “shot-noise” della luce di segnale;
b) nel rumore associato alla “emissione spontanea” presente in tutti gli
Amplificatori Ottici e dovuta al battimento fra lo stato vuoto ed il
momento di dipolo elettrico della transizione in esame.
Comunicazioni Ottiche, Capitolo 4, Edizione Ottobre 2007
25
La legge di Callen-Walton unisce una funzione “classica” (l’espressione
di Planck) con un comportamento quantistico. Bisogna fare attenzione
nella interpretazione di questo diagramma perché mentre l’energia
elettromagnetica di origine termica viene effettivamente prodotta e quindi
anche “catturata” dall’antenna o dai componenti del ricevitore, l’energia
dello “stato vuoto”, non viene mai direttamente ricevuta e quindi
“misurata”. Essa si manifesta tramite il “quantum noise” che si rileva
quando un “altro” segnale ottico è presente. Si suole affermare che
“l’energia dello stato vuoto non si estrae”.
L’ultima espressione dello spettro di potenza residuo quanto il solo
rumore ottico sia considerato, consente di fare una stima del rapporto
Segnale/Rumore aspettato in un ideale ricevitore ottico.
SNRottico =
potenza di segnale
Ps
=
potenza di rumore 1 h"B
2
dove B rappresenta la banda della rivelazione. Sapendo poi che
!
Ps = n ( t ) h"
ho che
!
quantum lim ited
SNRottico
=
!
ovvero considerando una banda bi-laterale pari a 2B (come ottengo con la
rivelazione coerente)
quantum lim ited
SNRottico
=
!
2n ( t )
B
n( t )
=n
B
Questo rapporto segnale/rumore è il più alto ottenibile in comunicazione
ottica ed è pari semplicemente al numero di fotoni misurato nel tempo di
osservazione: esso si chiama SNR quantum-limited.
Nel caso di un ricevitore “radio” la stessa stima porterebbe al valore di
SNRradio =
potenza di segnale
Ps
=
potenza di rumore kTB
A temperatura ambiente, secondo la legge di Wien, avrei una emissione
!
Comunicazioni Ottiche, Capitolo 4, Edizione Ottobre 2007
26
dominante alla lunghezza d’onda di
2,897 #10$3
"=
= 9,8 #10$6 m
296
!
cioè a frequenze dell’ordine di 300 GHz. La potenza di segnale è invece
costituita da “fotoni” radio, con frequenze dell’ordine dei GHz: non posso
quindi eseguire la “semplificazione” che ho fatto nella espressione del
SNR ottico, anzi mi occorrono molti “fotoni” radio (cioè molta potenza
radio) per sovrastare il rumore del kT.
Comunicazioni Ottiche, Capitolo 4, Edizione Ottobre 2007
27