1
Due atleti, Mario e Franco, stanno facendo una corsa. Franco parte 16,0 m dietro a Mario correndo alla velocità costante di 9,00 m/s. Se
Mario corre alla velocità costante di 28,8 km/h, calcolare dopo quanto tempo Franco raggiunge Mario e lo spazio percorso da Franco in
tale intervallo di tempo.
2
Un corpo si muove con una velocità
a.
b.
c.
d.
v 5,0
m
m
2,0 2 t .
s
s
Rappresentare il moto in un grafico velocità-tempo.
Scrivere la legge oraria del moto.
Calcolare la velocità del corpo dopo 5,0 s.
Calcolare lo spazio percorso nello stesso intervallo di tempo,sia utilizzando la legge oraria sia con il metodo grafico.
3
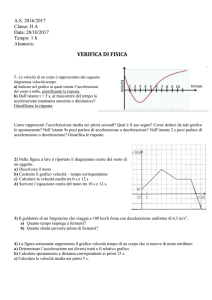
La velocità di un topolino in funzione del tempo è espressa dal grafico qui
riportato. Determinare l’accelerazione:
a. durante i primi 2,0 secondi;
b. tra il 2° e il 3° secondo;
c. la velocità dopo 4,0 secondi;
d. lo velocità media nell’intero percorso.
4
Un corpo si muove alla velocità di 40,0 m/s, rallenta poi con una
decelerazione pari a 5,0 m/s². Determinare:
a. la sua velocità dopo 6,0 s;
b. la sua velocità media durante i 6,0 secondi;
c. la distanza che percorre prima di fermarsi ed il tempo impiegato a fermarsi.
5
Un treno partito da fermo si muove con accelerazione costante. Ad un certo istante viaggia a 108 km/h e 160 m più avanti la sua velocità
è di 50 m/s. Calcolare:
a. l’accelerazione;
b. il tempo che impiega a percorrere i 160 m;
c. il tempo richiesto per raggiungere la velocità di 30 m/s;
d. la distanza tra il punto di partenza e quello in cui il treno ha raggiunto la velocità di 108 km/h.
1
Durante una corsa, Antonio passa davanti a un cartellone pubblicitario alla velocità di 6,00 m/s, mentre Bruno lo precede di un quarto di
kilometro e corre a 4,00 m/s. Supponiamo che entrambi si muovano con velocità costante. Stabilire a quale distanza dal cartellone
pubblicitario Antonio raggiunge Bruno e in quanto tempo.
2
Un corpo si muove con una velocità
v(m/s)
t(s)
a.
b.
c.
d.
v 8,0
m
m
1,0 2 t .
s
s
Rappresentare il moto in un grafico velocità-tempo.
Scrivere la legge oraria del moto.
Calcolare la velocità del corpo dopo 4,0 s.
Calcolare lo spazio percorso nello stesso intervallo di tempo,sia utilizzando la legge oraria sia con il metodo grafico.
3
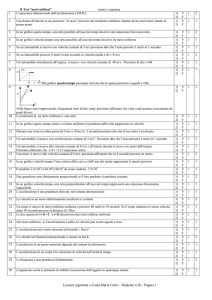
La velocità di un topolino in funzione del tempo è espressa dal grafico qui
riportato. Determinare l’accelerazione:
a. durante i primi 4,0 secondi;
b. tra il 4° e il 5° secondo;
c. la velocità dopo 6,0 secondi;
d. lo velocità media nell’intero percorso.
4
Un corpo si muove alla velocità di 60,0 m/s, rallenta poi con una
decelerazione pari a 4,0 m/s². Determinare:
a. la sua velocità dopo 5,0 s;
b. la sua velocità media durante i 5,0 secondi;
c. la distanza che percorre prima di fermarsi ed il tempo impiegato a fermarsi.
5
Un treno partito da fermo si muove con accelerazione costante. Ad un certo istante viaggia a 30 m/s e 160 m più avanti la sua velocità è
di 180 km/h. Calcolare:
a. l’accelerazione;
b. il tempo che impiega a percorrere i 160 m;
c. il tempo richiesto per raggiungere la velocità di 30 m/s;
d. la distanza tra il punto di partenza e quello in cui il treno ha raggiunto la velocità di 108 km/h.
v(m/s)
t(s)