Comportamento strutturale del patrimonio architettonico in muratura

Comportamento strutturale del patrimonio
architettonico in muratura:
criteri di modellazione
Sergio LAGOMARSINO
Dipartimento di Ingegneria delle Costruzioni,dell’Ambiente e del Territorio
Università degli Studi di Genova
[email protected]
Roma, 2 luglio 2008
Li
Linee
guida
id per lla valutazione
l t i
e riduzione
id i
d
dell rischio
i hi sismico
i i d
dell patrimonio
ti
i culturale
lt l
Corso di aggiornamento
Roma, complesso del San Michele. 30 giugno - 3 luglio 2008
Direttiva del Presidente del Consiglio dei Ministri – 12 ottobre 2007
(GU nn.25
25 del 29.1.2008,
29 1 2008 suppl
suppl.ord.
ord N
N. 24)
“Direttiva del Presidente del Consiglio dei Ministri per la valutazione
e la riduzione del rischio sismico del patrimonio culturale con
riferimento alle Norme Tecniche per le costruzioni”
Indice
1.
2.
3.
4.
5
5.
6.
Oggetto delle Linee Guida
Requisiti di sicurezza e conservazione
Azione sismica
Conoscenza del manufatto
Modelli per la valutazione della sicurezza sismica
Criteri per il miglioramento sismico e tecniche di
intervento
MODELLI PER LA VALUTAZIONE DELLA SICUREZZA SISMICA
Analisi territoriale
Valutazione sul singolo manufatto
LV1: analisi con modelli meccanici
semplificati o qualitativi
LV2: valutazione su singoli macroelementi
(progetto di interventi di restauro locali)
LV3: valutazione complessiva della
risposta del manufatto (progetto di un
intervento di restauro complessivo sul
manufatto)
a SLU
IS =
γ I Sa g
Capitolo 2 – Requisiti di sicurezza e conservazione
LIVELLI DI SICUREZZA
Nel caso del patrimonio culturale, considerato che ll’adeguamento
adeguamento sismico non
è obbligatorio e vincolante, è ragionevole confrontare la capacità sismica
con livelli di sicurezza di riferimento, opportunamente graduati con
riferimento
if i
t alla
ll rilevanza
il
culturale
lt l e all’uso
ll’
e ffunzione
i
svolti.
lti
Categorie
g
di rilevanza culturale: bassa,, media,, elevata
Categorie di uso: abbandonato o occasionale, frequente, molto frequente
Categoria d’uso
Categoria di rilevanza
Limitata
Media
Elevata
P eccedenza
d
γI
P eccedenza
d
γI
P eccedenza
d
γI
Saltuario o non utilizzato
40%
0.50
25%
0.65
17%
0.80
Frequente
25%
0 65
0.65
17%
0 80
0.80
10%
1 00
1.00
Molto frequente
17%
0.80
10%
1.00
6,5%
1.20
INGV-Istituto Nazionale di
Geofisica e Vulcanologia
DPC-Dipartimento della Protezione Civile
Convenzione INGV-DPC 2004 - 2006
Progetto S1
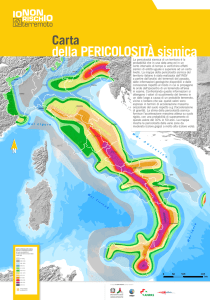
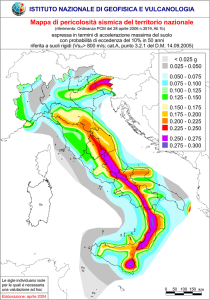
Pericolosità sismica per diverse probabilità di superamento in 50 anni: ag
C. Meletti, V. Montaldo
Probabilità di Corrispondente
eccedenza in
periodo di
50 anni
ritorno
Corrispondente
frequenza
annuale di
superamento
Dati
(scaricare il file)
81%
30
0.0332
(file zip - 631 kb)
63%
50
0.0199
(file zip - 642 kb)
50%
72
0.0139
(file zip - 651 kb)
39%
101
0.0099
(file zip - 657 kb)
30%
140
0.0071
(file zip - 650 kb)
22%
201
0.0050
((file zip
p - 666 kb))
10%
475
0.0021
MPS04
5%
975
0.0010
(file zip - 682 kb)
2%
2475
0.0004
(file zip - 686 kb)
http://esse1.mi.ingv.it/d2.html
Capitolo 5 – Modelli per la valutazione della sicurezza sismica
Intuizione dei meccanismi di collasso nelle strutture in muratura
Analisi limite dell’equilibrio
B
2
C
1
3
1
A
D
Modellazione non lineare ad elementi finiti
Comportamento sismico di costruzioni in muratura
I meccanismi di danno
Primo modo
Comportamento sismico di costruzioni in muratura
I meccanismi di danno
Primo modo
Comportamento sismico di costruzioni in muratura
I meccanismi di danno
Primo modo
Secondo modo
Seismic behaviour of masonry buildings
IN-PLANE MECHANISMS
C
S S
(2° failure mode)
OUT-OF-PLANE MECHANISMS
(1° failure
f il
mode)
d )
Seismic behaviour of masonry buildings
FLOORS and ROOF
Out-of-plane mechanisms (1° failure mode)
Seismic behaviour of masonry buildings
ANALISI STATICA NON LINEARE
fascia
maschio
nodo
MECCANISMI DI DANNO SISMICO NELLE CHIESE
Strutture molto vulnerabili:
• forma particolare
• elevate dimensioni
Non si realizza un comportamento
scatolare, ma più spesso si verifica
un meccanismo di danno locale
Macroelemento:
“parte della chiesa architettonicamente riconoscibile (facciata,
(f
abside, arco trionfale),
f ) caratterizzata da una risposta sismica autonoma dal
resto della fabbrica” (Doglioni et al. 1994)
Overturning of the church façade
Overturning of the church façade
Overturning of the façade gable
Overturning of the façade gable
Triumphal arches
Triumphal arches
Out-of-plane mechanisms of the lateral walls
Capitolo 5 – Modelli per la valutazione della sicurezza sismica
5.2 Livelli di valutazione della sicurezza sismica
5.2.1 LV1: analisi qualitativa con modelli meccanici semplificati
La valutazione LV1 consiste in una verifica semplificata da effettuarsi a scala territoriale
su tutto il patrimonio, in primo luogo per far fronte alla richiesta dell'OPCM 3274/03
(verifiche entro 5 anni) e per acquisire una conoscenza utile a fini preventivi e di
pianificazione degli interventi.
Tale strumento non può avere un'eccessiva complessità, quale è quella tipica dei calcoli
strutturali che sono eseguiti nel progetto di un intervento di restauro statico.
L'affidabilità del risultato è quindi ridotta, ma essendo l'obiettivo quello di stilare una
graduatoria dalla quale far emergere i manufatti più a rischio,
rischio ll'uso
uso di un unico
strumento oggettivo su un'intera tipologia costruttiva presenta notevoli vantaggi.
L’indice di sicurezza che si ottiene, anche se nella fase di programmazione viene usato
come indicatore comparativo, rappresenta comunque una stima quantitativa
dell'accelerazione sismica al suolo che produce un certo stato limite nella
costruzione.
Si sono adottati tre diversi modelli per i palazzi, le chiese e le torri.
Capitolo 5 – Modelli per la valutazione della sicurezza sismica
5.2.2 LV2: valutazione su singoli macroelementi (meccanismi locali)
Questo livello di valutazione si applica nei casi in cui sono previsti interventi di restauro
che interessano singole parti della costruzione. In questi casi è possibile utilizzare
modelli locali, riferiti a porzioni strutturalmente autonome della costruzione
((macroelementi).
) Tuttavia,, siccome l’Ordinanza richiede che per
p qualsiasi
q
intervento
di miglioramento venga calcolata l’accelerazione di collasso, relativamente al
manufatto nel suo complesso, la valutazione della sicurezza sismica complessiva
può essere stimata con gli strumenti del livello di valutazione LV1.
LV1
L’analisi cinematica, lineare o non lineare, rappresenta lo strumento in genere più
efficace ed agevole per tale valutazione; i risultati ottenibili possono però essere
eccessivamente cautelativi se non vengono considerati i diversi dettagli costruttivi
che determinano il comportamento reale: presenza di catene, ammorsamento tra
murature ortogonali, tessitura muraria, condizioni di vincolo degli orizzontamenti.
P ognii macroelemento,
Per
l
t il confronto
f t tra
t le
l accelerazioni
l
i i allo
ll stato
t t lilimite
it ultimo
lti prima
i e
dopo l’intervento consente di esprimere un giudizio sul grado di miglioramento
conseguito, evidenziando l’inutilità di alcuni interventi. Inoltre, considerando
l’accelerazione massima al suolo di riferimento nel sito, è possibile valutare
l’effettiva necessità degli interventi, che potrebbero essere evitati in alcune parti.
Capitolo 5 – Modelli per la valutazione della sicurezza sismica
5.2.3 LV3: valutazione complessiva della risposta del manufatto
In questo caso viene valutata la sicurezza sismica dell’intera costruzione, ovvero
l’accelerazione del suolo che porta allo stato limite ultimo la costruzione nel suo
complesso o singole sue parti significative (macroelementi). Il livello LV3 deve
essere adottato nella p
progettazione
g
di interventi diffusi nella costruzione e
quando il restauro riguarda un edificio di tipo strategico, per l’importanza sociale
di conoscere in modo attendibile la sicurezza di tali strutture.
La verifica complessiva della risposta sismica del manufatto non richiede
necessariamente il ricorso ad un modello globale della costruzione, ma è
possibile procedere alla scomposizione della struttura in parti (macroelementi), a
condizione che venga valutata la ripartizione delle azioni sismiche tra i diversi
sistemi strutturali, in ragione delle diverse rigidezze e dei collegamenti tra le
stesse. La valutazione può quindi essere eseguita con gli stessi metodi utilizzati
all lilivello
ll LV2
LV2, ma iin modo
d sistematico
i t
ti su ciascun
i
elemento
l
t ddella
ll costruzione.
t i
Confrontando i valori ottenuti nei diversi macroelementi si può evidenziare l’inutilità
di alcuni interventi: a) se il margine di miglioramento è modesto rispetto
all’impatto dell’intervento sulla conservazione; b) per l’eccessiva sicurezza
fornita ad alcuni macroelementi rispetto agli altri.
Capitolo 5 – Modelli per la valutazione della sicurezza sismica
5.4 Modelli di valutazione per tipologie
Il concetto di tipologia male si adatta a manufatti storici, che dovrebbero essere
considerati elementi unici della storia del costruire, per il modo con il quale sono
stati concepiti, realizzati e si sono trasformati nel tempo. Tuttavia, nella maggior
parte delle costruzioni storiche è possibile riconoscere caratteri ricorrenti.
ricorrenti
Vengono quindi fornite indicazioni esemplificative per l’analisi e la valutazione
della risposta sismica nel caso delle più diffuse tipologie di manufatti tutelati.
Vengono anche proposti modelli meccanici semplificati (LV1) per le verifiche da
eseguire sull’intero patrimonio culturale tutelato a scala territoriale, ai fini di una
valutazione preventiva del rischio.
5.4.1 Palazzi, ville ed altre strutture con pareti di spina ed orizzontamenti intermedi
grandi aule,, senza orizzontamenti intermedi
5.4.2 Chiese ed altre strutture con g
5.4.3 Torri, campanili ed altre strutture a prevalente sviluppo verticale
5.4.4 Ponti in muratura, archi trionfali ed altre strutture ad arco
Capitolo 5 – Modelli per la valutazione della sicurezza sismica
55.22 Livelli di valutazione della sicurezza sismica
5.2.1 LV1: analisi con modelli meccanici semplificati o a base statistica
5.4.1 Palazzi, ville ed altre strutture con pareti
di spina ed orizzontamenti intermedi
LV1 – Modello per i palazzi
Al fine di determinare l’ accelerazione al suolo che porta al raggiungimento delle
condizioni limite di collasso dell’edificio, occorre determinare, per tutti i piani,
l’accelerazione di collasso del piano (collasso per piano debole) e, in riferimento al
piano terra, l’accelerazione valutata considerando anche il meccanismo di collasso
uniforme (rottura delle fasce di architrave).
Il modello meccanico semplificato proposto fornisce una valutazione quantitativa
dell’accelerazione di collasso, nell’ipotesi che questo si verifichi per rottura delle
pareti nel proprio piano, nell’ambito di un comportamento complessivo del manufatto
Nel
e caso in cu
cui l’edificio
ed c o risultasse
su tasse p
più
ù vulnerabile
u e ab e nei
e riguardi
gua d d
di qua
qualche
c e
meccanismo locale (per carenza di collegamenti), rispetto al suo comportamento
globale, si dovrà valutare l’accelerazione orizzontale che porta allo stato limite
ultimo q
quel macroelemento e confrontarla con q
quella ottenuta dal modello nel
seguito illustrato.
LV1 – Modello per i palazzi
Capitolo 5 – Modelli per la valutazione della sicurezza sismica
5 2 1 LV1: analisi con modelli meccanici semplificati o a base statistica
5.2.1
5.4.1 Palazzi, ville ed altre strutture con pareti di spina ed orizzontamenti intermedi
Hp di base:
H
b
comportamento
t
t scatolare
t l
dell’edificio
d ll’ difi i – solo
l risposta
i
t delle
d ll pareti
ti nell
proprio piano
qF
SLU
Indice di sicurezza Is:
FSLU,xi
a
IS = SLU
γ ISa g
⎛ μ xi ξ xi A xi τdi ⎞
=⎜
⎟
βxi
⎝
⎠
e*MC(T )
=
γ ISa g
FSLU : resistenza a taglio dell’edificio , il pedice “xi”
indica ad esempio la direzione x e il piano generico iesimo dell’edificio
Capitolo 5 – Modelli per la valutazione della sicurezza sismica
5 2 1 LV1: analisi con modelli meccanici semplificati o a base statistica
5.2.1
5.4.1 Palazzi, ville ed altre strutture con pareti di spina ed orizzontamenti intermedi
Hp di base:
H
b
comportamento
t
t scatolare
t l
dell’edificio
d ll’ difi i – solo
l risposta
i
t delle
d ll pareti
ti nell
proprio piano
qF
SLU
Indice di sicurezza Is:
FSLU,xi
e*MC(T )
=
γ ISa g
⎛ μ xi ξ xi A xi τdi ⎞
=⎜
⎟
βxi
⎝
⎠
9 μ omogeneità di rigidezza e resistenza dei
maschi murari
9 β irregolarità geometrica in pianta
9 ξ tipo di rottura prevalente previsto per i
maschi
hi (1 taglio-0.8
t li 0 8 pressoflessione)
fl i
)
9 calcolo di τ di
Capitolo 5 – Modelli per la valutazione della sicurezza sismica
5 2 1 LV1: analisi con modelli meccanici semplificati o a base statistica
5.2.1
5.4.1 Palazzi, ville ed altre strutture con pareti di spina ed orizzontamenti intermedi
Hp di base:
H
b
comportamento
t
t scatolare
t l
dell’edificio
d ll’ difi i – solo
l risposta
i
t delle
d ll pareti
ti nell
proprio piano
qF
SLU
Indice di sicurezza Is:
a
IS = SLU
γ ISa g
e*MC(T )
=
γ ISa g
9 e* frazione di massa p
partecipante
p
Collasso del piano k-esimo
piano debole
uniforme
Collasso uniforme
9 C(T) spettro normalizzato, rapporto fra lo spettro di risposta elastico e l’accelerazione massima del terreno che tiene conto delle caratteristiche del sito (agS)
9 M massa sismica totale
LV1 – Modello per i palazzi
Sulla
S
ll b
base d
della
ll quantità
tità di setti
tti murarii portanti,
t ti d
delle
ll caratteristiche
tt i ti h d
della
ll
muratura, del numero di piani, della tipologia degli orizzontamenti,
della regolarità in pianta ed in elevato dell'edificio, attraverso semplici
formule si perviene ad una stima dell'accelerazione di collasso della
costruzione.
E' evidente che un'analisi
E
un analisi statica non lineare con un modello ad elementi
finiti (secondo le indicazioni dell'OPCM) fornirebbe una stima più
precisa, ma tale approccio è improponibile a scala territoriale.
Il modello consiste in una verifica a collasso semplificata, nell’ipotesi di
collasso per piano debole. Essa è congruente con quanto ammesso
dall’OPCM nel caso di edifici inseriti in aggregati edilizi, per i quali un
modello a telaio equivalente dell’intero edificio, senza considerare
l’interazione con le strutture adiacenti, avrebbe poco senso.
Per l’applicazione
l applicazione del modello è necessario acquisire un certo numero di
informazioni (pianta dell'edificio ai diversi piani, spessori murari, ecc.)
e questi dati possono essere introdotti nel database del MiBAC,
disponibile in internet
internet, che pro
provvede
ede in a
automatico
tomatico ad effett
effettuare
are la
valutazione.
LV1 – Modello per i palazzi
LV1 – Modello per i palazzi
PIANO 1
LV1 – Modello per i palazzi
PIANO 2
LV1 – Modello per i palazzi
PIANO 3
LV1 – Modello per i palazzi
Dati generali:
• Dati del monitoraggio
• Valutazione Culturale
• Fattori di Sensibilità
• Caratteristiche
geografiche
• Caratteristiche di
accessibilità
Rilievo:
• Rilievo ingombro
geografico
• Rilievi semplificati
• Altra Documentazione
Morfologia elementi:
• Struttura dei piani
• Rilievo Elementi
Strutturali
• Associazioni tra
Elementi
• Codifica
C difi d
degli
li elementi
l
ti
Definizione delle
Vulnerabilità
Stato di conservazione
• Danno strutturale
RIEPILO
OGO E CALCOLO
O Is
5.2.1 LV1: analisi con modelli meccanici semplificati o a base statistica
5.4.2 Chiese ed altre strutture con g
grandi aule,, senza orizzontamenti intermedi
L’osservazione sistematica dei danni subiti dal patrimonio storico architettonico a
seguito degli eventi sismici degli ultimi 30 anni (Friuli, 1976; Umbria e Marche, 1997;
Molise, 2002; Salò, 2004), in particolare per le chiese, ha portato a riconoscere un
comportamento sistematico per meccanismi di collasso nei macroelementi (parti
architettoniche caratterizzate da un comportamento
p
in certa misura autonomo))
LA SCHEDA DI RILIEVO DELLE CHIESE
A partire dal terremoto Umbria-Marche,
Umbria Marche il rilievo del danno in emergenza è stato
effettuato con una scheda che richiede un rilievo del livello di danno nei singoli
macroelementi, riconoscendo attraverso un giudizio qualitativo diagnostico il
meccanismo
i
di collasso
ll
attivato
tti t e lle ffonti
ti di vulnerabilità.
l
bilità
Questo approccio ha il necessario carattere speditivo e risulta utile per: a) agibilità;
b) opere di pronto intervento; c) stima dei costi; d) avviamento e controllo dei progetti.
Scomposizione in macroelementi
Ribaltamento della facciata
Meccanismi nel piano della
facciata
Meccanismi nella sommità della facciata
Protiro o nartece
Indice di
danno
1
id =
5N
28
∑d
k =1
k
Rilievo del danno e della vulnerabilità
Nel box vulnerabilità sono indicati una serie di presidi antisismici che possono contrastare
l’ tti i
l’attivazione
d l suddetto
del
dd tt cinematismo
i
ti
ed
d una serie
i d’indicatori
d’i di t i di vulnerabilità
l
bilità che
h possono
invece aumentare la propensione al danneggiamento. Per ognuno di essi, il rilevatore dovrà
evidenziare la presenza o l’assenza (Si – No), e nella colonna di destra esprimere un giudizio
sull’efficacia
sull
efficacia del particolare costruttivo,
costruttivo modulando il suo giudizio su tre diversi livelli (0:
inefficace; 1: modesto; 2: buona; 3: completamente efficace).
28
1∑
iv = k =1
6
ρ k (vki − vkp )
28
∑ρ
k =1
k
+
1
2
DPM (Matrici di Probabilità di danno)
Umbria
Imcs = V
Imcs = VI
06
0.6
Imcs = VII
06
0.6
d=0.20
0.5
Imcs = VIII
06
0.6
d=0.26
0.5
06
0.6
d=0.43
0.5
0.4
0.4
0.4
0.4
0.3
0.3
0.3
0.3
0.2
0.2
0.2
0.2
0.1
0.1
0.1
0.1
0.0
0.0
0
1
2
3
4
5
0.0
0
1
2
3
4
d=0.58
0.5
0.0
5
0
1
2
3
4
5
0
1
2
3
4
5
Marche
Imcs = V
Imcs = VI
06
0.6
Imcs = VII
d=0.22
06
0.6
06
0.6
06
0.6
0.5
Imcs = VIII
d=0.28
0.5
d=0.36
0.5
0.4
0.4
0.4
0.4
03
0.3
03
0.3
03
0.3
03
0.3
0.2
0.2
0.2
0.2
0.1
0.1
0.1
0.1
0
0
0
0
1
2
3
4
5
0
1
2
3
4
5
d=0.64
0.5
0
0
1
2
3
4
5
0
1
2
3
4
5
Modello LV1 per le chiese
a SLU = 0.025 ⋅ 1.8
a SLD = 0.025 ⋅ 1.8
Indice di vulnerabilità minimo per la verifica
nelle diverse zone (IS=1, per suolo A e γI=1).
5.1−3.44 i v
2.75−3.44i v
ag
0 35
0.35
0 25
0.25
0 15
0.15
0 05
0.05
SLU
0.18
0.34
0.6
1
SLD
S
0
00.11
00.37
3
00.91
9
0.5
SLU
accceleraziione
0.4
SLD
03
0.3
0.2
0.1
0
0
0.2
0.4
0.6
Indice di vulnerabilità iV
0.8
1
LV1 – Modello per le chiese
Il modello per le chiese è concettualmente diverso da quello per i palazzi.
Le tipologie architettoniche e le geometrie sono talmente diversificate da
rendere impossibile la messa a punto di un modello di calcolo analitico
semplificato; inoltre per le chiese una valutazione globale sull'intera
fabbrica avrebbe poco senso, in quanto il collasso si verifica
di ti t
distintamente
t sulle
ll singole
i
l parti
ti (facciata,
(f
i t abside,
b id ecc.).
)
Meccanismi locali si verificano anche negli edifici, ma prevalentemente nel
costruito minore dei centri storici, mentre nei palazzi la qualità dei
collegamenti è sufficiente a garantire un comportamento globale.
Per le chiese si è quindi proposto un modello LV1 basato su una lettura
attenta
tt t delle
d ll caratteristiche
tt i ti h costruttive
t tti
d ll fabbrica,
della
f bb i
neii diversi
di
i
elementi architettonici che la compongono (macroelementi); in
particolare, sulla base delle specifiche vulnerabilità riscontrate (scarsa
qualità muraria, assenza di collegamenti, presenza di elementi
spingenti, ecc.) e della presenza di elementi costruttivi di presidio
antisismico (catene, contrafforti, ecc.) viene calcolato un punteggio,
denominato indice di vulnerabilità.
LV1 – Modello per le chiese
Questo indice avrebbe un significato puramente qualitativo; tuttavia
essendo stato valutato a seguito dei recenti terremoti in Italia (UmbriaM h Molise,
Marche,
M li
S lò ecc.)) è stato
Salò,
t t possibile
ibil stabilire,
t bili
t
tramite
it questo
t
indice, una correlazione statistica tra l'accelerazione sismica e lo stato
limite di danno o collasso prodotto.
In
altre parole, noto l'indice di vulnerabilità posso risalire
all'accelerazione sismica al suolo corrispondente ai diversi stati limite.
La base dati statistica è molto ampia (oltre 3000 chiese) e la confidenza
della valutazione è molto buona.
Questo modello ha il limite di non essere basato su una valutazione
meccanica, ma ha il pregio di tener conto esplicitamente
(diversamente dal modello dei palazzi), di tutte le informazioni
qualitative frutto della conoscenza diretta sul manufatto.
LV1: analisi qualitativa con modelli meccanici semplificati
A li i
Applicazione
a 12 chiese
hi
danneggiate
d
i t d
dall’evento
ll’
t sismico
i i d
della
ll LLombardia
b di del
d l 2004
Azione sismica di riferimento
Pericolosità del sito
γISa
S max
Evento sismico 2004
IMCS
a SLU = 0.025 ⋅ 1.8 5.1−3.44i v
amax
a SLD = 0.025 ⋅1.8 2.75−3.44i v
ar
a
o
ola
t
rtin
o
tol
om
e
ma
c
ar
ll'I
m
S.
B
de
Ma
zia
rin
o
di
Sc
o
d'A
g
S.
gh
er
i ta
Ch
ies
a
S.
M
elo
nd
re
a
Ar
ca
ng
S.
Pi
er
ele
.A
ita
or
cia
iov
aN
att
ist
a
eG
iS
tin
o
le
d
ich
ch
ia
au
s
S.
M
Pa
rro
c
SS
:F
od
an
ni
B
de
tt
o
S.
An
dr
ea
S.
Cr
oc
ifis
s
iov
rio
S
S.
G
tua
S.
Be
ne
Sa
n
Is
Pericolosità del sito – Stato limite ultimo
2.5
20
2.0
1.5
1.0
0.5
0.0
ar
io
SS
S.
An
.C
ro
cif
iss
o
dr
ea
Gi
ov
an
ni
S.
Ba
Be
ttis
ne
ta
de
tto
da
SS
No
:F
rci
au
a
sti
n
Pa
oe
rro
Gi
cc
ov
hia
ita
le
di
S.
An
S.
dr
Mi
ea
ch
ele
Ar
ca
ng
elo
S.
Pi
er
S.
d'A
Ma
gr
ino
rg
he
rita
di
Sc
oz
ia
S.
Ch
Ma
ies
rtin
ad
o
ell
'Im
ma
co
lat
a
S.
Ba
rto
lom
eo
S.
Sa
ntu
Is
Pericolosità del sito – Stato limite danno
2.5
20
2.0
1.5
1.0
0.5
0.0
en
ed
ett
od
aN
S.
or
cia
Gi
ov
an
Pa
ni
rro
Ba
cc
ttis
hia
ta
le
di
S.
An
dr
ea
S.
An
S.
dr
Mi
ea
ch
ele
Ar
Ch
ca
ies
ng
ad
elo
ell
'Im
S.
ma
Ma
co
lat
rg
he
a
rita
di
Sc
oz
ia
S.
Sa
Ma
ntu
rtin
ar
io
o
SS
.C
ro
ci f
i ss
o
S.
Ba
rto
SS
lom
:F
au
eo
sti
no
eG
iov
ita
S.
Pi
er
d'A
gr
ino
S.
B
Is
Evento sismico 2004 – Stato limite ultimo
12
11
10
9
Id = 0.65
8
7
6
5
4
3
2
1
0
S.
Be
ne
de
tt
od
aN
Mi
ch
ele
Ar
S.
dr
ea
ca
ng
An
elo
de
ll'I
mm
S.
ac
Ma
ola
rg
ta
he
rita
di
Sc
oz
ia
S.
Sa
Ma
ntu
rtin
ar
io
o
SS
.C
ro
c if
iss
o
S.
Ba
rto
SS
lom
:F
au
eo
sti
no
eG
iov
ita
S.
Pi
er
d'A
gr
ino
Ch
ies
a
S.
or
Gi
cia
ov
an
Pa
ni
rro
Ba
cc
ttis
hia
ta
le
di
S.
An
dr
ea
S.
Is
Evento sismico 2004 – Stato limite danno
3
2
Id = 0
0.02
02
Id = 0.05
1
Id = 0.1
Id = 0.05
0
Capitolo 5 – Modelli per la valutazione della sicurezza sismica
55.22 Livelli di valutazione della sicurezza sismica
5.2.1 LV1: analisi con modelli meccanici semplificati o a base statistica
5.4.3 Torri, campanili ed altre strutture a
prevalente sviluppo verticale
Chiesa di S.Maria Assunta
(Gemona)
Chiesa di S.Stefano (Cavazzo
Carnico)
S.Pietro e Paolo (Maiano)
Capitolo 5 – Modelli per la valutazione della sicurezza sismica
5 2 1 LV1: analisi con modelli meccanici semplificati o a base statistica
5.2.1
5.4.3 Torri, campanili ed altre strutture a prevalente sviluppo verticale
Hp di base: la torre è schematizzata come una mensola,
mensola sollecitata da un sistema di
forze orizzontali oltre che dal proprio peso, che può andare in crisi in una generica
sezione per schiacciamento nella zona compressa a seguito della parzializzazione
dovuta alla non resistenza a trazione
Verifica a
pressoflessione:
M u,i, =
σ 0i Ai ⎛
2
σ 0i Ai ⎞
⎜ bi −
⎟
0 85 i f d ⎠
0.85a
⎝
9 M u,i
u i è il momento corrispondente al collasso per presso
flessione della sezione i-esima di analisi;
9 ai è il lato perpendicolare alla direzione dell’azione sismica
considerata della sezione i-esima di analisi,
d
depurato
t d
dalle
ll eventuali
t li aperture;
t
9 bi è il lato parallelo alla direzione dell’azione sismica
considerata della sezione di analisi;
9 Ai è l’area totale della sezione di analisi;;
9 σ0i è la tensione normale media nella sezione di analisi
9 fd è la resistenza a compressione di calcolo della muratura
(tenendo conto del fattore di confidenza FC).
Capitolo 5 – Modelli per la valutazione della sicurezza sismica
5 2 1 LV1: analisi con modelli meccanici semplificati o a base statistica
5.2.1
5.4.3 Torri, campanili ed altre strutture a prevalente sviluppo verticale
Momento agente
di calcolo:
9 F h = 0.85Sd(T1)W/g;
9 Wi e Wk sono i pesii d
deii settori
tt i i e k rispettivamente;
i
tti
t
9 zi e zk sono le altezze dei baricentri dei settori i e k rispetto alle fondazioni;
9 Sd((T1) è l’ordinata dello spettro
p
di risposta
p
di p
progetto,
g
funzione del p
primo
periodo T1 della struttura secondo la direzione considerata;
9 W=ΣWi è il peso complessivo della struttura;
9 g è l’accelerazione
l accelerazione di gravità
gravità.
Risultante delle
forze sismiche nella
sezione i-esima
Altezza cui
applicare Fhi
Capitolo 5 – Modelli per la valutazione della sicurezza sismica
5 2 1 LV1: analisi con modelli meccanici semplificati o a base statistica
5.2.1
5.4.3 Torri, campanili ed altre strutture a prevalente sviluppo verticale
Definiti Mu,i , Fhi e zhi dai
passi precedenti
Uguaglianza tra momento
ultimo e momento di progetto
Valore dell’accelerazione massima
del suolo corrispondente al
raggiungimento dello stato limite
ultimo nella sezione i-esima
Capitolo 5 – Modelli per la valutazione della sicurezza sismica
Allegato B - L’analisi strutturale delle costruzioni storiche in muratura
• La muratura
• La modellazione strutturale
• I metodi di analisi
5 2 Metodi di analisi
5.2
1.
2
2.
3.
4.
Analisi statica o cinematica lineare
Analisi dinamica modale
Analisi statica o cinematica non lineare
Analisi dinamica non lineare
ANALISI STATICA LINEARE
•
Il metodo agli elementi finiti in campo lineare può essere molto utile per
lo studio delle condizioni in esercizio di una struttura (ruolo dei diversi
elementi, stati di tensione e deformazione). Tuttavia è necessaria una
attenta modellazione delle connessioni tra gli elementi e delle fasi
costruttive e di trasformazione.
ANALISI STATICA LINEARE
•
•
•
L azione sismica di riferimento al suolo
L’azione
suolo, per lo stato limite ultimo
ultimo, viene in
questo caso ridotta attraverso il fattore di struttura, per consentire una
verifica in campo elastico; in questo modo si tiene implicitamente conto
delle ulteriori capacità di spostamento, una volta raggiunta la massima
resistenza (difficoltà di stimare appropriati fattori di struttura).
Il modello deve essere sottoposto ad un sistema di forze orizzontali:
a) distribuzione di forze proporzionale alle masse; b) distribuzione di forze
proporzionale al principale modo di vibrazione, eventualmente adattato
it ti
iterativamente.
t Il periodo
i d di vibrazione
ib i
potrà
t à essere stimato
ti t anche
h
ipotizzando una forma modale principale (metodo di Rayleigh-Ritz).
L’analisi
L
analisi elastica ad elementi finiti ha poco significato per una struttura
complessa, in quanto i valori puntuali dello stato tensionale nel materiale
muratura devono essere confrontati per la verifica con i valori di resistenza
d l materiale.
del
t i l Con
C questa
t analisi
li i sii riscontrano,
i
t
generalmente,
l
t tensioni
t i i di
trazione, non accettabili nella muratura, o elevate tensioni di compressione,
influenzate dalla mesh ((concentrazioni tensionali).
) Le verifiche p
puntuali
potrebbero quindi non essere soddisfatte anche in condizioni lontane dallo
stato limite ultimo (sovraresistenza).
ANALISI STATICA LINEARE
•
•
Nel caso di palazzi e ville
ville, ovvero di edifici caratterizzati da pareti di spina
ed orizzontamenti intermedi, è possibile fare ricorso ad un modello a telaio
equivalente, che consente una verifica a livello dell’elemento strutturale
(elementi portanti verticali e orizzontali) e non di tipo puntuale. In questo
caso, essendo le condizioni di verifica del singolo elemento riferite a
condizioni locali fessurate,
fessurate l’analisi
l analisi statica lineare può essere considerata
maggiormente significativa.
Nel caso in cui l’analisi sismica sia basata sulla valutazione distinta di
di
diversi
i meccanismi
i i llocali,
li sia
i per una valutazione
l t i
complessiva
l i d
dell
manufatto, sia per una verifica nelle sole zone oggetto di intervento, è
possibile utilizzare gli strumenti dell
dell’analisi
analisi limite, in particolare nella forma
del teorema cinematico. L’analisi cinematica lineare, come definita
nell’Ordinanza (Allegato 11.C), consiste nel calcolo del moltiplicatore
orizzontale
i
t l dei
d i carichi
i hi che
h attiva
tti il meccanismo
i
di collasso
ll
e nella
ll
valutazione della corrispondente accelerazione sismica al suolo. Per la
verifica allo SLU,, tale accelerazione viene confrontata con q
quella di
riferimento, ridotta attraverso un opportuno fattore di struttura.
INFLUENZA DELLE FASI DI COSTRUZIONE E TRASFORMAZIONE
Edificio Galata, Porto Antico di Genova
Analisi stratigrafica ed individuazione delle fasi storiche
Modellazione ad elementi finiti delle diverse fasi
ANALISI NON LINEARE PER FASI
Fase 1
PARETE DI SPINA
CENTRALE
Fase 2
Fase 3
ANALISI NON LINEARE IN UNICA FASE
MPa
-1.5
-1.0
-0.5
-0.1
0.0
+0.1
La Basilica di San Francesco d’Assisi
dal 1228 al XIV secolo
Influenza delle fasi costruttive
La Basilica di San Francesco d’Assisi
XIV secolo
Influenza delle fasi costruttive
La Basilica di San Francesco d’Assisi
1475
Influenza delle fasi costruttive
La Basilica di San Francesco d’Assisi
1957
Influenza delle fasi costruttive
Tensioni Verticali di
compressione nelle
pareti laterali
phase
1
phase
2
Analisi in 1 fase
1+2
Spostamento alle
imposte delle volte
before
step
Analisi per Analisi in 1
fasi
fase
2
4.7
1.9
3
5.5
3.4
4
6.5
3.7
phase
3
1957
after
phase
4
1957
Capitolo 5 – Modelli per la valutazione della sicurezza sismica
5.2 Metodi di analisi
ANALISI DINAMICA MODALE
•
•
•
L’analisi modale con spettro di risposta presuppone la sovrapposizione
degli effetti e regole di combinazione modale calibrate su strutture a telaio;
è quindi scarsamente attendibile,
attendibile specie nel caso di strutture complesse
complesse,
caratterizzate da trasformazioni e fasi costruttive differenti. In questi casi,
considerare il contributo dei modi superiori
p
può
p avere poco
p
significato,
g
per
p
la forte nonlinearità dei materiali e la presenza di giunti strutturali.
Può essere utilizzata con maggiore confidenza in presenza di strutture
flessibili e strutturalmente ben modellabili,
modellabili come ad esempio le torri,
torri i
campanili o altre strutture a prevalente sviluppo verticale. In questi casi
possono risultare importanti i contributi dei modi superiori. Resta tuttavia la
difficoltà di determinare opportuni fattori di struttura.
Può essere utilizzata per stimare il modo principale di vibrazione nelle due
direzioni e determinare quindi un
un’attendibile
attendibile distribuzione di forze da
adottare nell’analisi statica lineare o non lineare.
Capitolo 5 – Modelli per la valutazione della sicurezza sismica
5.2 Metodi di analisi
1.
2.
3.
4
4.
Analisi statica o cinematica lineare
Analisi dinamica modale
Analisi statica o cinematica non lineare
A li i dinamica
Analisi
di
i non lineare
li
ANALISI STATICA NON LINEARE
•
•
L’analisi statica non lineare consiste nella valutazione del comportamento sismico
della struttura fino a collasso (legame forza-spostamento)
forza spostamento) ed in particolare della
capacità di spostamento allo stato limite ultimo, da confrontare con lo spostamento
richiesto dal terremoto.
Tale analisi può essere eseguita con un modello che rappresenti il comportamento
globale della costruzione (modello ad elementi finiti), adottando legami costitutivi
non lineari.
Capitolo 5 – Modelli per la valutazione della sicurezza sismica
5.2 Metodi di analisi
ANALISI STATICA NON LINEARE
•
•
L’analisi statica non lineare consiste nella valutazione della capacità di
spostamento allo stato limite ultimo (legame forza-spostamento), da
confrontarsi con lo spostamento richiesto dal terremoto,
terremoto valutato in termini
spettrali su un sistema equivalente ad 1 gdl. Tale analisi può essere
eseguita
g
con un modello che rappresenti
pp
il comportamento
p
globale
g
o
attraverso modelli di sottostrutture (macroelementi), con verifiche locali.
La curva di capacità della struttura può essere derivata dal legame forzaspostamento ottenuto attraverso un
spostamento,
un’analisi
analisi incrementale ad elementi finiti
finiti,
utilizzando legami costitutivi non lineari e, se necessario, considerando la
non linearità geometrica. L’analisi consiste nell’applicare i carichi
gravitazionali ed un sistema di forze orizzontali, che vengono scalate,
mantenendo invariati i rapporti relativi tra le stesse, in modo da far crescere
monotonamente lo spostamento orizzontale di un punto di controllo,
controllo fino al
raggiungimento delle condizioni ultime.
ANALISI STATICA NON LINEARE
•
•
Individuazione della capacità di spostamento ultimo: 1) se il modello è in
grado di descrivere la perdita di resistenza (softening), grazie a legami
costitutivi sofisticati e/o condizioni limite sugli spostamenti dei singoli
elementi strutturali, esso sarà definito in corrispondenza di una riduzione
della reazione massima orizzontale pari al 20%; 2) nel caso di legame elastoplastico o di solido non resistente a trazione
trazione, l’analisi
l analisi sarà portata avanti
fino a spostamenti significativi, senza la necessità di definire uno
spostamento limite ultimo. La conversione del legame forza-spostamento
generalizzato in sistema bi-lineare equivalente sarà effettuata con i metodi
noti. Considerata la difficoltà di definire lo spostamento allo stato limite
ultimo, il rapporto tra la forza di risposta elastica e la forza massima del
sistema bi-lineare equivalente non potrà superare un valore massimo
ammissibile, definito in base alle caratteristiche di duttilità e dinamiche
proprie
i di ciascuna
i
titipologia
l i e comunque compreso ttra 3 e 66.
Nel caso di palazzi e ville, ovvero di edifici caratterizzati da pareti di spina
ed orizzontamenti intermedi,, è p
possibile fare riferimento a modelli a telaio
equivalente.
Vulnerability of Colonial churches in Puebla and Oaxaca
regions (Mexico) – 1999 earthquake
(in cooperation with Prof. R. Meli Piralla)
Piralla)
• Damage assessment
• Non linear f.e.m. of a prototype
nonlinear layered shell
Capitolo 5 – Modelli per la valutazione della sicurezza sismica
5.2 Metodi di analisi
1.
2.
3.
4
4.
Analisi statica o cinematica lineare
Analisi dinamica modale
Analisi statica o cinematica non lineare
A li i dinamica
Analisi
di
i non lineare
li
ANALISI CINEMATICA
•
Nello studio dei meccanismi locali si può usare l’analisi limite dell’equilibrio,
secondo l’approccio proposto da Heyman (e da Giuffrè nel caso sismico)
Capitolo 5 – Modelli per la valutazione della sicurezza sismica
5.2 Metodi di analisi
ANALISI CINEMATICA NON LINEARE
•
•
In alternativa al metodo degli elementi finiti, anche nel caso di un’analisi
non lineare è possibile fare ricorso all’analisi limite, attraverso un’analisi per
cinematismi
i
ti i di collasso,
ll
assegnando
d incrementalmente
i
t l
t all cinematismo
i
ti
configurazioni variate in spostamenti finiti di entità crescente. Questa
prende il nome di analisi cinematica non lineare e consente di valutare le
p
capacità di spostamento del sistema dopo che il meccanismo si è attivato.
La procedura per la determinazione del sistema bi-lineare equivalente e per
la valutazione della risposta massima in spostamento (spettro elastico al 5%
di smorzamento, con rigidezza secante) è descritta nell’Allegato 11.C
dell’Ordinanza. La Circolare esplicativa delle nuove Norme Tecniche, di
prossima pubblicazione, propongono un metodo leggermente modificato.
ANALISI LIMITE DELLE STRUTTURE MURARIE
Il collasso delle costruzioni in muratura avviene in genere per perdita di
equilibrio di porzioni strutturali piuttosto che per il raggiungimento della
tensione di rottura del materiale.
Ipotesi
• materiale non resistente a trazione (gli elementi costituenti la muratura
sono fragili,
fragili la malta di calce è debole
debole, giunti a secco o degradati)
• infinita resistenza a compressione (in genere la muratura è poco sollecitata
rispetto alle tensioni di rottura locale per compressione)
• materiale indeformabile (le strutture murarie sono in genere tozze
tozze,
comunque non sensibili agli effetti di non linearità geometrica)
• assenza di scorrimenti nei giunti (l’attrito inibisce gli scorrimenti, a parte
casi p
particolari;; la validità dell’ipotesi
p
può
p
essere verificata a posteriori)
p
)
HEYMAN (1969)
Dimostra la validità dei teoremi dell
dell’analisi
analisi limite
anche per le murature
Afferma che una struttura in muratura è equilibrata
q
se è possibile trovare una curva delle pressioni che
si mantenga ovunque all’interno del solido murario
Analisi limite dei telai
q
λP
Assegnata una struttura ed una
distribuzione di carichi, permanenti ed
accidentali,, valutare λ, il moltiplicatore
p
di questi ultimi che porta al collasso
q
λP
Collasso locale
• momento plastico MP: massimo momento
sopportabile
soppo
tab e nella
e a se
sezione
o e
MP
• cerniera plastica:
plastica raggiunto MP in una sezione,
si introduce una cerniera ed i momenti plastici
(il momento
t non può
ò più
iù crescere in
i quella
ll
sezione per i successivi incrementi di carico)
MP
I TEOREMI DELL’ANALISI LIMITE
Teorema statico
Scegliere il moltiplicatore di collasso nell
nell’insieme
insieme dei
moltiplicatori staticamente ammissibili λ−
• λ− è qualsiasi moltiplicatore per il quale sia possibile trovare
una soluzione
l i
equilibrata
ilib
(non
(
necessariamente
i
congruente),
)
con sollecitazioni ammissibili in ogni sezione (M≤MP)
Teorema cinematico
Scegliere
g
il moltiplicatore
p
di collasso nell’insieme dei
moltiplicatori cinematicamente sufficienti λ+
• introduco nel sistema un numero di cerniere plastiche tali
da trasformare la struttura in un cinematismo di elementi che
considero rigidi (struttura labile)
• λ+ è il moltiplicatore associato al cinematismo, ottenuto
applicando il teorema dei lavori virtuali,
virtuali che fornisce una
distribuzione di azioni equilibrate per il sistema labile
I TEOREMI DELL’ANALISI LIMITE
Si dimostra:
• per l’insieme
l insieme dei moltiplicatori statici:
• per l’insieme dei moltiplicatori cinematici:
λ = max { λ− } = min { λ+ }
Come posso determinare λ:
• teorema statico
statico: analisi incrementale
• teorema cinematico:
cinematico analisi per tentativi
λ− ≤ λ
λ+ ≥ λ
Applicazione del TEOREMA STATICO
Metodo operativo:
1. risolvo la struttura iperstatica
2 determino la sezione più sollecitata ed introduco una cerniera
2.
plastica (cerniera + momento plastico)
3. risolvo la nuova struttura, che presenta un grado di iperstaticità
ridotto di uno rispetto alla precedente
4. eseguo più volte i passi 2 e 3, fino alla trasformazione della
struttura in un sistema isostatico
5. determino λ in modo che si formi
f
l’ultima cerniera plastica, che
trasforma il sistema in labile e quindi coincide con il collasso
2λP
λP
2λP
λP
2λP
2λP
λP
λP
(λ−3)MP
MP
MP
MP
(λ−2)
(λ
2)MP
MP
MP
MP
MP
MP
MP
λ=3
Applicazione del TEOREMA CINEMATICO
M d operativo:
Metodo
i
1. ipotizzo un cinematismo di collasso, posizionando un numero
sufficiente di cerniere plastiche
2. determino le rotazioni virtuali nelle cerniere plastiche e gli
spostamenti virtuali dei punti di applicazione delle forze esterne
3 calcolo il moltiplicatore corrispondente a quel possibile
3.
cinematismo, attraverso il teorema dei lavori virtuali
4. eseguo più volte i passi 1, 2 e 3, scegliendo diversi possibili
cinematismi di collasso
5. seleziono il moltiplicatore più basso tra i λ+ (la stima è a sfavore di
sicurezza a meno che se tra essi non ci sia il meccanismo giusto)
2λP
θa
MP
λP
C3
(3)
MP
(1)
MP
MP
(2)
θ
θ
C1
C2
λP θ a = MP ((θ+θ+θ+θ))
MP = P a
λ=4
Applicazione del TEOREMA CINEMATICO
M d operativo:
Metodo
i
1. ipotizzo un cinematismo di collasso, posizionando un numero
sufficiente di cerniere plastiche
2. determino le rotazioni virtuali nelle cerniere plastiche e gli
spostamenti virtuali dei punti di applicazione delle forze esterne
3 calcolo il moltiplicatore corrispondente a quel possibile
3.
cinematismo, attraverso il teorema dei lavori virtuali
4. eseguo più volte i passi 1, 2 e 3, scegliendo diversi possibili
cinematismi di collasso
5. seleziono il moltiplicatore più basso tra i λ+ (la stima è a sfavore di
sicurezza a meno che se tra essi non ci sia il meccanismo giusto)
C3
2λP
θa
λP
MP
MP
2θ
(1 )
θa
(3)
(2 )
C1
MP
MP
θ
C2
λP θa + 2λP θa = 10 Pa θ
λ = 3.33
3 33
Applicazione del TEOREMA CINEMATICO
M d operativo:
Metodo
i
1. ipotizzo un cinematismo di collasso, posizionando un numero
sufficiente di cerniere plastiche
2. determino le rotazioni virtuali nelle cerniere plastiche e gli
spostamenti virtuali dei punti di applicazione delle forze esterne
3 calcolo il moltiplicatore corrispondente a quel possibile
3.
cinematismo, attraverso il teorema dei lavori virtuali
4. eseguo più volte i passi 1, 2 e 3, scegliendo diversi possibili
cinematismi di collasso
C3
2λP
θa
λP
MP
MP
λP θa + 2λP θa/2 = 6 Pa θ
θ a/2 (3)
(1)
MP
MP
(2)
θ
θ
C1
C2
λ=3
L’ANALISI A COLLASSO DELLE STRUTTURE MURARIE
Data una struttura muraria, soggetta a carichi permanenti e accidentali,
voglio sapere di quanto possono crescere i secondi prima del collasso.
Applicazione
A li
i
del
d l TEOREMA STATICO
Metodo operativo (analisi incrementale):
1. suddivido la struttura in conci e valuto i carichi agenti su ciascuno
2. ipotizzo un valore del moltiplicatore λ dei carichi accidentali e cerco
una curva delle pressioni staticamente ammissibile
3. se la trovo, incremento ulteriormente il carico (λ+Δλ
λ+Δλ) e cerco
nuovamente una curva delle pressioni ammissibile
4 continuo finché non riesco più a equilibrare il carico
4.
λ− -
il massimo dei moltiplicatori
p
staticamente
ammissibili potrebbe non essere ancora il vero λ
vantaggi – il risultato è a favore di sicurezza
svantaggi – procedimento laborioso
Applicazione del TEOREMA CINEMATICO
Trasformo
T
f
la
l struttura
t tt
iin un cinematismo
i
ti
di bl
blocchi
hi rigidi,
i idi introducendo
i t d
d
un numero strettamente sufficiente di cerniere.
Il collasso locale si verifica quando la curva delle pressioni lambisce il
bordo esterno della sezione; questa situazione corrisponde a mettere in
quel punto una cerniera, in quanto i due blocchi sono liberi di ruotare
Metodo operativo (analisi per tentativi):
1. Ipotizzo diversi cinematismi e calcolo per ciascuno il moltiplicatore
cinematico, applicando il teorema dei lavori virtuali sulle forze
esterne (le forze interne sono nulle in quanto MP=0)
• in ogni blocco occorre valutare le forze peso, proporzionali al
volume del blocco ed applicate nel suo baricentro
• dalla catena cinematica si valutano gli spostamenti virtuali dei
baricentri dei blocchi e dei punti di applicazione delle forze
λ+ -
il minore dei moltiplicatori
p
cinematici valutati
potrebbe essere maggiore di quello esatto
vantaggi – procedimento semplice e rapido
svantaggi – a sfavore di sicurezza, specie se non si hanno
indicazioni sul possibile meccanismo di collasso
Ponte ferroviario di PRAROLO
Epoca di costruzione: 1850-53
Caratteristiche geometriche:
- Luce: 40 m
- Spalle troncoconiche (alte 22 m, φ 20 m)
- Arcata di sezione variabile, prosegue
nelle pile ca
cave,
e con contrafforti (frenelli)
- Obliquo rispetto al torrente Scrivia
- Intradosso convesso
METODI DI SOLUZIONE
• costruzione del modello CAD 3D
• verifica grafica CAD parametrico
ANALISI DI UN ARCO CON CARICO CONCENTRATO
ANALISI STATICA
λ=3.6
ANALISI DI UN ARCO CON CARICO CONCENTRATO
ANALISI CINEMATICA
λ=5.8
λ=4
ANALISI DI UN ARCO CON CARICO CONCENTRATO
ANALISI STATICA
ANALISI CINEMATICA
λ=3.6
λ=4
L’ANALISI SISMICA
Si t
Sistema
rigido
i id - le
l forze
f
sismiche
i i h orizzontali
i
li sono:
FH = W amax/g
(forza apparente di trascinamento, senza amplificazione dinamica)
Il problema sismico delle strutture murarie
Analisi a collasso con
con:
• azioni permanenti costanti
• forze orizzontali proporzionali ai carichi permanenti, tramite λ
λ = amax/g
Come d
C
definire
fi i il meccanismo
i
di collasso
ll
per una chiesa?
hi
?
MACROELEMENTO: parte della chiesa architettonicamente riconoscibile ((facciata, abside, arco trionfale),
) caratterizzata da una risposta
sismica sostanzialmente autonoma dal resto della fabbrica
MECCANISMO DI COLLASSO: i diversi modi con i quali giungono a
collasso i macroelementi,, al variare di geometria
g
e tecniche costruttive, sono stati sistematicamente osservati (Le chiese e il terremoto,
abaco della scheda chiese, codici di pratica)
MECHANICAL-BASED METHOD FOR MONUMENTS
Δx1 = θ1(yA-y1) Δy1 = θ1(x1- xA)
Δx2 = θ1(yA-yB)+θ2(yB-y2) Δy2 = θ1(xB-xA)+θ2(x2-xB)
Δx3 = θ3(yD-y3) Δy3 = θ3(x3-xD)
Δl = θ3(ycatena-yD) - θ1(ycatena-yA)
C2
2
λ
3
C3
1
C1
Prove su tavola vibrante eseguite presso ENEA Casaccia, Roma
Progetto TREMA – ENEA, DPC, Università della Basilicata, ReLUIS
O.P.C.M. n. 3274 del 21/03/2003 e s.m.i.
Allegato 11
11.C
C
Suggerisce la valutazione della vulnerabilità sismica dei
meccanismi locali attraverso l’utilizzo
l utilizzo dell
dell’Analisi
Analisi Limite
dell’Equilibrio secondo un approccio cinematico
• Definizione del meccanismo di collasso
• Valutazione accelerazione che attiva il meccanismo
• Andamento dell’azione che la struttura è in grado di
sopportare all’evolversi del meccanismo
Analisi Cinematica Lineare
Analisi Cinematica Non Lineare
Analisi Limite – APPROCCIO CINEMATICO
Per ogni possibile meccanismo locale ritenuto significativo per l’edificio,
il metodo si articola nei seguenti passi:
1. trasformazione della parte di costruzione in un sistema labile
(catena cinematica), attraverso l’individuazione di corpi rigidi,
definiti da piani di frattura,
frattura in grado di ruotare o scorrere tra loro
Analisi Limite – APPROCCIO CINEMATICO
2 Valutazione
2.
V l t i
d l moltiplicatore
del
lti li t
orizzontale
i
t l dei
d i carichi
i hi a0 che
h genera
l’attivazione del meccanismo
⎛ n
α 0 ⎜ ∑ Pi δ x,
xi
⎜ i =1
⎝
P i i i dei
Principio
d i Lavori
L
i Vi
Virtuali
t li
n+m
o
⎞ n
⎟
+ ∑ P j δ x,
x j ⎟ − ∑ Pi δ y,
y i − ∑ Fh δ h = L fi
j= n +1
h =1
⎠ i =1
α0
F1
α0P1
P1
θ1
((11.C.1))
Analisi cinematica lineare: la capacità della
struttura è definita dall’accelerazione
spettrale che attiva il meccanismo a0*
a *0
α0
=
n +m
∑ Pi
i =1
*
M
=
α 0g
e*
Analisi Limite – APPROCCIO CINEMATICO
3. Valutazione
V l t i
dell’evoluzione
d ll’ l i
ddell moltiplicatore
lti li t
d
deii carichi
i hi α all crescere
dello spostamento dk del punto di controllo, scelto in prossimità del
baricentro fino all’annullamento
baricentro,
all annullamento della forza sismica orizzontale;
Passo 0
α0
Passo 1
0.06
α1
Passo i
αi
0.05
0.04
Legame α –
L
spostamento
generalizzato
0.03
0.02
Spostamento
punto
t di controllo
t ll
0.01
0
0
0.1
0.2
dk [m]
0.3
0.4
Analisi Limite – APPROCCIO CINEMATICO
4. Trasformazione della curva ottenuta in curva di capacità, ovvero in
accelerazione a* e spostamento d* spettrali
α
α
Accelerazione spettrale a*
a =
*
n +m
∑P
i
i =1
*
M
n+m
dk
0.6
Spostamento spettrale d
d*
d* = d k
2
a* [m/s ]
0.5
2
P
δ
∑ i x,i
i =1
n+m
δ x,k ∑ Pi δ x,i
i =1
0.4
0.3
0.2
0.1
0
0
0.1
0.2
d* [m]
0.3
0.4
αg
= *
e
Analisi dei meccanismi locali di collasso in edifici esistenti
Approccio
A
i in
i spostamenti:
t
ti per considerare
id
l risorse
le
i
i fase
in
f
non lineare
li
come evidenziato dall’osservazione dei danni e da campagne sperimentali
CURVA DI CAPACITA’
Teq = 2π
a eq
d eq
• Rappresentazione come SDOF equivalente
• Capacità in termini di spostamento (quota parte dello spostamento
per cui l’equilibrio è possibile solo in assenza di azione sismica)
• Controllo di altre condizioni limite locali (sfilamento di travi, ecc.)
Analisi dei meccanismi locali di collasso in edifici esistenti
Approccio
A
i in
i spostamenti:
t
ti per considerare
id
l risorse
le
i
i fase
in
f
non lineare
li
come evidenziato dall’osservazione dei danni e da campagne sperimentali
14
9
Equivalent SDOF system
Analitycal formulation
10
θ lim = arctg(B/H)
λ= H/B
8
6
Analytical formulation
7
Period T (s)
12
Equivalent SDOF system
8
4
6
5
4
3
β = 125°
s/R = 0.06
θ lim = 0.0385 rad
2
2
1
0
0
0
0.2
0.4
0.6
θ 0/θ lim
0.8
(a)
1
0
0.2
0.4
0.6
θ0/θ lim
0.8
1
(b)
Analisi Limite – APPROCCIO CINEMATICO
5 V
5.
Verifica
ifi di sicurezza,
i
attraverso
tt
il confronto
f t ttra DOMANDA e
CAPACITÀ.
Analisi Cinematica Lineare
Verifica semplificata in termini di accelerazione spettrali
a ≥
*
0
( )
a g PVR S
Accelerazione massima al suolo
q
Se (T1 ) ⋅ ψ (Z) ⋅ γ
a ≥
q
*
0
CAPACITÀ
Accelerazione massima a quota Z
DOMANDA
azione sismica (zona
(zona, terreno
terreno, ecc
ecc.))
q è il fattore di struttura uguale a 2.0.
Analisi Limite – APPROCCIO CINEMATICO
5 Verifica
5.
V ifi di sicurezza,
i
confronto
f t DOMANDA/CAPACITÀ
Analisi Cinematica Non Lineare
Confronto tra la capacità di spostamento ultimo du* del meccanismo
locale e la domanda di spostamento Dd.
d*u ≥
SDe (Ts ) ⋅ ψ (Z) ⋅ γ
2
⎛ Ts ⎞
Ts
1
−
+
0
0.02
02
⎜
⎟
T1
⎝ T1 ⎠
CAPACITÀ
DOMANDA
Azione sismica
(zona, terreno, …)
OSSERVAZIONI
• E’ necessario individuare correttamente i meccanismi da analizzare
α0P2
P2
α0P1
P1
θ1
Ribaltamento globale con buon ammorsamento
OSSERVAZIONI
• E’ necessario individuare correttamente i meccanismi da analizzare
C2
θ2
α0P2
P2
C12
α0P1
P1
θ1
C1
Presenza di solaio intermedio spingente
OSSERVAZIONI
• E’ necessario considerare la qualità della muratura
ARRETRAMENTO
DELLE CERNIERE
OSSERVAZIONI
• E’ possibile valutare l’efficacia di interventi di rinforzo
F1
α0P1
P1
θ1
Presenza di incatenamento (forza esterna)
ANALISI SISMICA DI SANTA MARIA DEL MAR - BARCELLONA
5th Framework
Frame ork E
European
ropean Commission Project
Project: RISK
RISK-UE
UE
An advanced approach to earthquake risk scenarios
with applications to different European towns
SANTA MARIA DEL MAR, BARCELLONA
La chiesa di Santa Maria del Mar è una delle principali opere del gotico catalano.
catalano
La costruzione iniziò nel 1329 (XIV secolo). La facciata presenta due torri poligonali ai lati,
realizzate successivamente,
successivamente ed un grosso rosone.
rosone LL’interno
interno è a tre navate
navate, senza transetto
transetto.
La chiesa subì due terremoti:
• in occasione del terremoto del 1373 (epicentro nei
Pirenei, intensità VIII-IX), mentre la chiesa era in costruzione, ci fu qualche lieve danno alla torre campanaria;
• durante il terremoto del 1428 (intensità epicentrale VIII)
ci fu il crollo del rosone, con la morte di diverse persone.
Fructuós
F
t ó M
Maña
ñ
J. Irizarry, X. Goula, T. Susagna, A. Roca
Geometría de Santa María del Mar
26m
37.5m
15m
15m
Vistas Interiores de la Iglesia
g
z
z
z
Las 3 naves de la iglesia, cubiertas con bóvedas de crucería, logran crear
la sensación de una única nave .
El gótico
óti catalán
t lá se distingue
di ti
por ell uso dde contrafuertes
t f t en vez dde
arbotantes
El espacio entre las naves
laterales y los contrafuertes se
incluye dentro del interior de la
estructura para crear capillas.
macroelemento
MODELLO GEOMETRICO DELLA COSTRUZIONE
colonne
pareti laterali, archi
trasversali, contrafforti
volte
l
MODELLO GEOMETRICO DELLA COSTRUZIONE
Total width
Central nave
Side nave
Central bay
35.2 m
13.6 m
10 8 m
10.8
13.6 m
Total height
Central vault springings
Lateral vault springings
32.2 m
23.4 m
18.9 m
Total volume
Vault volume: central nave
Vault volume: side naves
Vault volume: chapels
p
Pillars
Counterforts and walls
Colonne:
σ = 11.55 N/mm2
Pareti laterali: σ = 0.45 N/mm2
1350.43
1350
43
59.31
72.15
17.53
69.56
1131.88
m3
m3
m3
m3
m3
m3
Tensioni medie di compressione
MODELLO STRUTTURALE
AD ELEMENTI FINITI
z
Analisi dinamica modale, per stimare il periodo
fondamentale di vibrazione
T = 0.78 s
z
Analisi incrementale a collasso con un legame
costitutivo non lineare per la muratura.
meccanismo di collasso
ANALISI INCREMENTALE A COLLASSO
Localizzazzione fessure
T i i di compressione
Tensioni
i
CURVA DI CAPACITA’ SISMICA
analisi
li i cinematica
i
ti iincrementale,
t l su configurazioni
fi
i i ddeformate
f
t
CURVA DI CAPACITA’ SISMICA
analisi
li i cinematica
i
ti iincrementale,
t l su configurazioni
fi
i i ddeformate
f
t
Arretramento negli arconi
Arretramento
A
t
t nelle
ll colonne
l
e nelle
ll paretiti
laterali/contrafforti (coeff. di sicurezza 3)
CURVE DI CAPACITA’ SISMICA
I fl
Influenza
della
d ll resistenza
i t
a compressione
i
ddell materiale
t i l
STATI LIMITE DI DANNO E COLLASSO
C f t con i risultati
Confronto
i lt ti dell’analisi
d ll’ li i non lilineare add elementi
l
ti fifiniti
iti
RISPOSTA SISMICA CON LO SPETTRO DI BARCELLONA
Il lilivello
ll di danno
d
atteso
tt
è moderato
d t ((comparsa di ffessure))
Zone 1
Probabilistic spectrum
Senza arretramento
!!
Definizione di spettri a quote diverse dalla base dell’edificio
L’analisi è stata concentrata sulle celle campanarie in quanto sono
risultate il macroelemento maggiormente vulnerabile.
S. Stefano – Nocera Umbra - (PG)
Tarcento – (UD)
S. Maria Assunta - Casacco - (UD) S. Lorenzo - Sabbio Chiese – (BS)
S. Maria delle Grazie – Salò - (BS) S. Maria Assunta - Sellano (PG)
SS Trinità di Monteaperta Taiapana – (UD)
S. Stefano – Cesclans - (UD)
Definizione di spettri a quote diverse dalla base dell’edificio
Accelerogramma
di input per la cella
?
Accelerogramma
cce e og a a d
di
input per la cella
Accelerogramma
all suolo
l
⎧T2
⎪ 2
⎪ Tr
⎪
n ⎪
⎪
Δ (T ) = ∑ ⎨
2
r =1 ⎪ T
⎪ 2
⎪ Tr
⎪
⎪⎩
S D e ( Tr ) γ rψ r ( z )
2
⎡ ⎛ T ⎞⎤
0.02 ⎛ T ⎞
⎢1 − ⎜
⎟⎥ +
⎜
⎟
η D 2 (ξ s ) ⎝ Tr ⎠
⎣ ⎝ Tr ⎠ ⎦
S D e ( Tr ) γ rψ r ( z )
2
⎡ ⎛ T ⎞⎤
⎛T ⎞
⎢1 − ⎜
⎟ ⎥ + 0.02 ⎜
⎟
⎝ Tr ⎠
⎣ ⎝ Tr ⎠ ⎦
⋅ η D (ξ s )
T ≤ Tr
T > Tr
Domanda di spostamento
per meccanismi locali
secondo la nuova
Circolare esplicativa delle
N
Norme
T
Tecniche
i h (di
prossima pubblicazione)
Proposta di una formulazione per la definizione dello spettro
16
35
A
14
Sa[m/s ]
2
2
Sa[m/s ]
25
10
8
6
F
4
0.5
1.0
T [s]
1.5
25
B
20
40
15
C
10
0.0
0.5
1.0
T [s]
1.5
2.0
E
35
D
30
2
2
0
E
2.0
Sa[m/s ]
0.0
Sa[m/s ]
15
5
0
25
20
15
10
5
B
5
0
0
0.0
25
0.5
1.0
T [s]
1.5
2.0
A
60
C
20
0.0
0.5
1.0
T [s]
1.5
2.0
F
50
40
15
2
Sa[m/s ]
2
20
10
2
Sa[m/s ]
D
30
12
10
Chiesa di S. Martino
Resiutta (UD)
5
0
0.0
0.5
1.0
T [s]
1.5
2.0
Spettri da
analisi numerica
30
20
10
0
0.0
0.5
Formulazione
analitica
1.0
T [s]
1.5
2.0
Definizione di spettri a quote diverse dalla base dell’edificio
L formulazione
La
f
l i
nell’OPCM
ll’OPCM per valutare
l t
l’incremento
l’i
t dello
d ll spettro
tt di
risposta non pare però del tutto adeguata
NUOVA PROCEDURA SEMPLIFICATA
derivata da una formulazione che definisce i floor response spectra
⎧T2
⎪ 2
⎪ Tr
⎪
n ⎪
⎪
Δ (T ) = ∑ ⎨
2
r =1 ⎪ T
⎪ 2
⎪ Tr
⎪
⎪⎩
S D e ( Tr
) γ rψ r ( z )
2
⎡
⎛ T ⎞⎤
0 .0 2 ⎛ T ⎞
⎢1 − ⎜
⎟⎥ +
⎜
⎟
η D 2 (ξ s ) ⎝ T r ⎠
⎝ Tr ⎠ ⎦
⎣
S D e ( Tr
) γ rψ r ( z )
2
⎡
⎛ T ⎞⎤
⎛T ⎞
⎢1 − ⎜
⎟ ⎥ + 0 .00 2 ⎜
⎟
⎝ Tr ⎠ ⎦
⎝ Tr ⎠
⎣
Tipologia
p g
Periodo
Tr (s)
Edifici, palazzi
(n = numero di piani)
0.05 H3/4
Chiese
Campanili, torri
⋅ η D (ξ s )
T ≤ Tr
T > Tr
Coeff. di partecipazione modale γr
3n
2n + 1
H
altezza della struttura
0.07 H3/4
1.1
quota di gronda
0.04 H
1.5
quota di gronda
quota di colmo
Verifica di meccanismi locali tramite Spettri di
Risposta in Spostamento: esempio applicativo
Chiesa di San Nicola di Bari a Macchia
Valforte (CB)
Sposstamento (m))
0.14
curva di capacità
spettro
du*
retta T*u
0.12
0.1
0.08
0.06
0.04
0.02
0
0
0.5
1
1.5
2 2.5 3
Periodo T (s)
3.5
4
4.5
5
Spostam
mento (m)
0.25
Spettro
C r a di capacità
Curva
d*u
T*u
0.20
0.15
0.10
0.05
0.00
0
0.5
1
Periodo T (s)
1.5
2
Esempio di applicazione
• Isolato dal resto della fabbrica;
• Danneggiamento
D
i
t principalmente
i i l
t
concentrato nella cella e composto da
lesioni evidenti.
Esempio di applicazione
Dal danneggiamento
gg
rilevato sono stati analizzati due meccanismi di collasso
Meccanismo 1
Meccanismo 2
Applicando il Teorema dei Lavori Virtuali è stato possibile valutare il moltiplicatore
orizzontale α0 dei carichi e la sua evoluzione al crescere dello spostamento di un
punto di controllo dk ((baricentro del corpo
p
p 2).
) La curva di capacità
p
è stata ottenuta
trasformando il moltiplicatore α in accelerazione spettrale a* e dk in spostamento
spettrale d* secondo quanto proposto nell’OPCM 3431/05.
Esempio di applicazione
Meccanismo 1
Meccanismo 2
40
4.0
3.5
2
a [m/s ]
2.5
2.0
*
*
2
a [m/s ]
3.0
1.5
1.0
0.5
0.0
0
0.02
0.04
0.06
*
d [m]
0.08
0.1
0.12
44.55
4.0
3.5
3.0
25
2.5
2.0
1.5
1.0
0.5
0.0
0
0.05
0.1
0.15
0.2
0.25
*
d [m]
Applicando il Teorema dei Lavori Virtuali è stato possibile valutare il moltiplicatore
orizzontale α0 dei carichi e la sua evoluzione al crescere dello spostamento di un
punto di controllo dk ((baricentro del corpo
p
p 2).
) La curva di capacità
p
è stata ottenuta
trasformando il moltiplicatore α in accelerazione spettrale a* e dk in spostamento
spettrale d* secondo quanto proposto nell’OPCM 3431/05.
0.3
*
2
a [m/s ]
Esempio di applicazione
4.5
4.0
3.5
3.0
2.5
2.0
15
1.5
1.0
05
0.5
0.0
Meccanismo 1
0
0.02
0.04
Meccanismo 2
0.06
0.08
0.1
0.12
0.14 * 0.16
d [m]
Il meccanismo 1 risulta maggiormente vulnerabile sia in termini di
accelerazione di attivazione, sia in termini di duttilità.
Esempio di applicazione
Determinazione della PGA al suolo corrispondente
p
alla determinazione della
condizione ultima della cella.
14
Curva di capacità
Sa [m/s2]
Spettro alla base del- 12
la cella per una PGA
al suolo pari a 1m/s2 10
Spettro alla base della
cella corrispondente
alla PGA di collasso
8
6
4
2
0
0 00
0.00
0 04
0.04
0 08
0.08
Sd [m]
0 12
0.12
0 16
0.16
0 20
0.20
Esempio di applicazione
30
30
Suolo A
Suolo A
25
Suolo
B-C-E
25
20
Sa [m/s2]
20
2
Sa [m/s ]
Suolo B-C-E
15
15
10
10
5
5
0
0
0
0.04
0.08 S [m] 0.12
d
24
0.16
0.2
0
0.04
0.08
Sd [m]
0.12
0.16
Suolo D
Suolo D
20
2
Sa [m/s ]
16
12
PGA al suolo
2.03 m/s2
4
Suolo
A
0
B-C-E
1.54 m/s2
D
1 22 m/s
1.22
/ 2
8
0
0 04
0.04
0 08 S [m] 0.12
0.08
0 12
d
0 16
0.16
02
0.2
0.2
5.2 Metodi di analisi
ANALISI DINAMICA NON LINEARE
•
•
•
L’analisi dinamica non lineare richiede modelli non lineari ad elementi finiti
(o a telaio equivalente),
equivalente) purché i legami costitutivi siano in grado di simulare
non solo il degrado di rigidezza e resistenza (a livello puntuale o di singolo
elemento strutturale),
) ma anche le caratteristiche dissipative
p
associate al
comportamento ciclico isteretico. Questo metodo di analisi non può
prescindere dall’esecuzione, con lo stesso modello strutturale, di un’analisi
statica non lineare
lineare, al fine di determinare la capacità di spostamento ultimo
della struttura, eventualmente attraverso una limitazione della duttilità.
L’analisi dinamica non lineare presuppone l’utilizzo di diversi gruppi di
accelerogrammi (almeno tre) selezionati in modo da risultare compatibili
con lo spettro di risposta corrispondente al tipo di sottosuolo.
L’utilizzo
L
utilizzo di questo metodo di analisi è limitato a casi particolari,
particolari quando la
complessità della struttura e l’importante contributo di diversi modi di
vibrazione non consentono di definire in modo attendibile un sistema non
lineare equivalente ad un solo grado di libertà. Le richieste di spostamento
sono in genere inferiori a quelle dell’analisi statica non lineare.
CONCLUSIONI
La grande sfida per gli ingegneri e gli architetti che si occupano degli
aspetti strutturali è contribuire in modo decisivo nella definizione del
giusto punto di equilibrio tra sicurezza e conservazione: a tal fine è
opportuno un uso combinato di valutazioni qualitative e quantitative.
Nel secolo scorso gli interventi di consolidamento sul costruito storico
sono stati progettati senza usare modelli meccanici; ciò ha prodotto:
• Interventi pesanti ed invasivi (scelti a priori, seguendo una prassi)
• Interventi leggeri (decisi su base qualitativa; volendo operare
“ t l ti
“cautelativamente”,
t ” spesso sono stati
t ti realizzati
li ti interventi
i t
ti inutili)
i tili)
Attraverso un uso corretto (non dimenticando i loro limiti), i modelli di
calcolo possono rappresentare uno strumento decisivo per una
conservazione consapevole degli edifici storici, anche in area sismica.