Coordinate_ppt

ASTRONOMICAL COORDINATE SYSTEMS TOPICS: Main coordinate systems The effects of Earth’s mo;on Defini;ons and ;me measurements Necessità di conoscere posizione nello spazio e nel tempo di un oggeEo: • Per poterlo localizzare • Per poter studiare il suo moto: • Mo; apparen; (dipendono dal sistema di riferimento) • Mo; propri (intrinseci dell’oggeEo) La determinazione (molto precisa) delle posizioni e dei mo; propri cos;tuisce l’oggeEo dell’ Astrometria Assegnare le coordinate a un oggeEo (o a un insieme di oggeJ) in un frame si chiama: astrometrizzazione Mol; di ques; riferimen; spaziali e temporali sono sta; inizialmente sviluppa; sopraEuEo per esigenze civili, militari e religiose: orientamento, determinazione della longitudine in mare, computo del tempo, computo della Pasqua, etc. Board of longitudes (GB – 1714): cospicuo premio in denaro per lo sviluppo di un metodo per la determinazione della longitudine in mare. Bureau des longitudes (Fr -­‐ 1795): “reprendre la maîtrise des mers aux anglais, grâce à l´améliora;on de la détermina;on des longitudes en mer (les la;tudes se déterminent facilement) qui ne peut se faire que par l
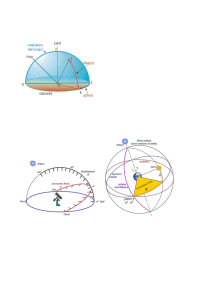
´observa;on astronomique et l´u;lisa;on d'horloges fiables.” hEp://www.bureau-­‐des-­‐longitudes.fr/ US Naval Observatory (USA): Pubblica dal 1852 The Nau+cal Almanac. Alcuni dei principali cataloghi astronomici (USNO, NOMAD, etc. ) sono cura; dall’US N.O. hEp://www.usno.navy.mil/ Meridiana di S. Maria degli Angeli (Roma)  Computo accurato del tempo per scopi religiosi Principali sistemi di Coordinate Celes; Alt-­‐Azimutale (Horizontal Coordinate System): usato Equatoriale (Equatorial CS): quello più u;lizzato GalaJco (Galac;c CS): usato nell’astronomia galaJca ed extragalaJca Meno usa;, o comunque u;lizza; in ambi; specifici: SupergalaJco EcliJco In tuJ i sistemi di coordinate astronomici NON ci poniamo il problema della distanza TuJ gli oggeJ astronomici sono immagina; pos; “alla stessa distanza” su un’ipote;ca Sfera Celeste. Fissato un punto di riferimento tuEo quello che ci occorre è specificare una Direzione, ovvero un Angolo. Coordinate alt-­‐azimutali Azimuth – Az In senso orario a par;re da N Cerchio ver;cale North pole Altezza (Al;tude)-­‐Alt South pole Meridiano Locale Alt = 0 – 90°, Az = 0 – 360° Pro: Coordinate locali di “facile” determinazione Contro: Variano con;nuamente nel tempo Le montature dei grandi telescopi moderni sono alt-­‐azimutali, ma richiedono un controllo da computer. Coordinate Equatoriali In senso an;orario a par;re dal punto γ
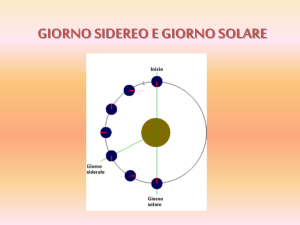
ProieEano sulla sfera celeste il sistema di meridiani e paralleli terrestri Ascensione ReEa (AR, RA, α) in h,m,s, da 0 a 24h Declinazione (Dec, δ) da -­‐90° a +90° Es.: M31: RA 00 42 44, Dec +41 16 09 α 00h42m44s, δ +41°16’09” Il punto di partenza della AR è il punto gamma (γ) – o punto Vernale o punto dell’Ariete: intersezione della proiezione dell’equatore terrestre e dell’ecliJca. L’ AR si misura in senso an+orario rispeEo a punto γ. L’ AR cos;tuisce un “orologio siderale”: l’ AR di un oggeEo che passa al meridiano locale in quel momento definisce il tempo siderale locale (LST). Sono le ore 00 00 00 di tempo siderale locale quando il punto γ transita al meridiano. Immaginate il meridiano locale come una lanceEa che indica il tempo “segnato” dall’ AR sull’equatore celeste. Conoscendo il LST e l’ AR di un oggeEo si può determinare il suo Angolo Orario (Hour Angle) cioè l’angolo di cui dobbiamo spostarci in ascensione reEa per trovare l’oggeEo: HAobject = LST – αobject Se HA è posi;vo dobbiamo spostarci verso Ovest, se è nega;vo verso Est. Conoscendo α, δ e LST siamo sempre in grado di puntare un oggeEo. Nel sistema di coordinate equatoriali solo una coordinata (l’angolo orario) cambia nel tempo e in maniera regolare. Nelle montature equatoriali il telescopio deve muoversi con una velocità angolare costante (360°/23h56m4s ≈ 0.0042°/sec, velocità siderale) solo aEorno all’asse polare per tenere puntato un oggeEo. Ma: Come facciamo a conoscere l’ora siderale locale (LST)? Dalla: HAobject = LST – αobject Si vede che se HA = 0 l’AR coincide con il LST: Il tempo siderale locale coincide con l’AR che in quel momento transita al meridiano RispeEo al punto γ la Terra compie una rotazione completa in un Giorno Siderale (circa 23h56m4s di tempo solare). I circa 4 minu; in più che portano alle 24 ore del Giorno Solare Medio sono dovu; al faEo che, a causa del suo spostamento lungo l’orbita, la Terra deve compiere una ulteriore rotazione di circa 1° per riportare il Sole al Meridiano. Per questo mo;vo ogni sera gli astri an+cipano il loro sorgere di circa 4 minu;. Il Giorno Siderale (e il conseguente secondo siderale) sarebbero troppo scomodi per usi civili. Come facciamo a CALCOLARE il LST per una data ora ? • Trovate l’algoritmo sulle dispense e scrivete un piccolo programma… • Lo calcolate in rete, es.: hEp://www.csgnetwork.com/siderealjulian;mecalc.html • (il tempo da inserire è quello di Greenwich !) • Lo guardate su di un soxware planetario Viceversa: nota l’AR di un oggeEo quando transiterà al meridiano di noEe ? Indica;vamente: Periodo dell’anno Transitano al meridiano di noTe gli oggeU con AR compresa tra: Equinozio primavera 7 -­‐ 17 Sols;zio estate 15 -­‐ 21 Equinozio autunno 19 -­‐ 5 Sols;zio inverno 0 -­‐ 12 Giorno Solare e Ora Solare Giorno Solare: intervallo di tempo che intercorre tra due passaggi del Sole allo stesso meridiano. Meridano di riferimento: Greenwich Ora solare di riferimento: GMT (Greenwich Mean Time), UT (Universal Time), UTC (Coordinated Universal Time). Sono le ore 12:00:00 UT quando il Sole passa al meridiano di Greenwich (in prima approx.) Time zones (tempo civile) – occhio ai daylight savings!... Per tuEo il centro Europa (Italia inclusa): CET (Central European Time): GMT + 1 . LSMT (tempo locale solare medio): dipende dalla longitudine del luogo Tempo medio e tempo apparente 2a legge di Keplero la velocità della Terra non è costante lungo l’orbita l’angolo di rotazione per riportare il Sole al meridiano cambia nel corso dell’anno non tuJ i giorni hanno durata uguale! Si definisce un giorno medio e un tempo medio. Per conoscere il mezzogiorno astronomico e quindi il tempo solare apparente (transito effeJvo del Sole al meridiano per quel giorno) si usa l’Equazione del Tempo per correggere il tempo medio Il punto gamma transita al meridiano di Greenwich Equatore celeste Notare come, a causa dell’equazione del tempo, il mezzogiorno astronomico non coincide con l’UT Per calcolare separazioni angolari possiamo esprimere l’AR in gradi: Poiché 24h360°: 1h 15° 4m 1° Etc… Ma AEenzione! L’effeJva separazione angolare (sulla sfera) dipende dalla declinazione… ESERCIZIO Calcolare la separazione angolare delle seguen; coppie di stelle: A: 1 (01 00 00, +45°00’00”), 2 (02 00 00, +45°00’00”) B: 1 (03 30 15, +5° 00’ 00”), 2 (03 30 15, +75°00’00”) C: 1 (12 25 30, +38°23’12”), 2 (14 23 22, +42°21’05”) Ma, abbiamo un problema… La variazione nell’orientazione dell’asse terrestre Il punto γ cambia nel tempo! L’asse di rotazione Terrestre (la cui orientazione determina la posizione del punto γ) si muove: • Precessione degli equinozi (periodo 25.725 yr circa – anno platonico, oscillazione max. circa 56°) • Nutazione (periodo principale 18.6 yr, oscillazione max: meno di 20”) • Altre perturbazioni (a volte difficilmente calcolabili sul lungo periodo) Le coordinate astronomiche (equatoriali) cambiano nel tempo e vanno riferite a un’Epoca. Un’Epoca è un istante. L’ul;ma Epoca di riferimento sono le ore 12 dell’1 gennaio 2000 (J2000.0) Siamo poi in grado di calcolare (con buona approssimazione) come variano nel tempo rispeEo a quell’Epoca. Correzione per la Precessione: p_RA = m + n * sin (RA) * tan (Dec) p_Dec = n * cos (RA) m = + 46.124" + 0.000279" * t = 3.0749 s + 0.0000186 s * t n = + 20.043" -­‐ 0.000085" * t = 1.3362s -­‐ 0.0000056 s * t Tranquilli: i so@ware planetari lo fanno automa+camente!... Nei cataloghi recen; trovate, accanto alle coordinate (RA, Dec): EquJ2000.0, ma potete anche trovare EquJ1950.0 A causa della nutazione si definisce, anche per il tempo siderale, un tempo medio e un tempo apparente (al livello delle nostre precisioni possiamo tranquillamente ignorare la differenza… ) Coordinate GalaJche -­‐ Galac;c Coordinate System (GCS) -­‐90° -­‐ b (la;tudine galaJca) -­‐ 90° 0° -­‐ l (longitudine galaJca) -­‐ 360° North Galac;c Pole: 12h 51m 26.282s, +27° 07’ 42.01″ (J2000) SagiEarius A* : l = 359° 56’ 39.5”, b = −0° 2’ 46.3″ La Data Giuliana (Jiulian Date -­‐ JD) Conta il tempo in giorni (e frazioni decimali di giorno) a par;re da un t0 t0 = ore 12 (tempo di Greenwich) del 1° gennaio 4713 avan; Cristo. Sistema introdoEo da Giuseppe Scaligero nel 1583 Sulla base di un ciclo (giuliano) basato su altri cicli (indizione, metonico, solare,… Vantaggi: • Indipendente dai calendari (e dalle loro modifiche) • Decimale: facile fare i con;! • Conta i giorni a par;re da mezzogiorno, per includere nella stessa JD un’intera noEe (tuEe le osservazioni di quella noEe appartengono alla stessa JD) Le 10:30, ora locale (11:30 UTC) di oggi (25/02/2011) corrispondono a JD = 2455617.89583 JD dell’1 gennaio 2000 ore 12 = 2451545.0 1 secondo = 0.00001157 JD Nelle dispense trovate un algoritmo per calcolare la JD a par;re dalla data di Calendario Gregoriano. Geocentrico o Topocentrico ?... I sistemi di coordinate celes; riferi; alla Terra sono Geocentrici (il centro del sistema di riferimento coincide con il centro della Terra) Ma noi osserviamo da un punto sulla superficie Per corpi vicini può fare una grande differenza I sistemi di riferimento in pra;ca Un sistema di riferimento deve essere basato su di un frame fisico A esempio, il sistema di riferimento delle coordinate geografiche (la;tudine e longitudine) sulla Terra è fisicamente realizzato da (almeno) tre satelli; della costellazione GPS. La distanza da tre pun; di riferimento nello spazio è sufficiente per individuare univocamente ogni punto dello spazio. Ma se abbiamo più di tre pun; siamo più precisi. Nel caso astronomico: La maggior parte delle posizioni nei cataloghi sono di natura differenziale, cioè sono rela;ve a un insieme di stelle (o altri oggeJ) di riferimento di posizione nota con grande precisione che cos;tuiscono un catalogo fondamentale. I più usa;: FK4 (1500 stelle brillan;, 1964) FK5 (circa 4500 stelle, fino al 1998) AEualmente: ICRS. Interna;onal Celes;al Reference System ICRS e ICRF L’Interna;onal Celes;al Reference System (ICRS) è il sistema di riferimento celeste fondamentale adoEato dall’IAU per l’astronomia di posizione di alta precisione. Si basa su di una serie di assi di riferimento individua; dalla posizione di un certo numero di sorgen;. Differenza tra un Sistema di Riferimento e un Frame di Riferimento: Un frame di riferimento consiste non di pun; “ideali”, ma di un catalogo di posizioni (e mo;, se misurabili) di stelle o di oggeJ extragalaJci vis; dal baricentro del Sistema Solare a una specifica Epoca. Idealmente sono sufficien; due posizioni sulla sfera per definire un frame. L’ICRF è un catalogo di posizioni di 608 sorgen; radio extragalaJche (di cui 212 definiscono il frame) la cui posizione, misurata con tecniche interferometriche radio (VLBI), è determinata con precisione dell’ordine del millesimo di secondo d’arco. Per una traEazione estesa: hEp://www.usno.navy.mil/USNO/astronomical-­‐applica;ons/astronomical-­‐
informa;on-­‐center/icrs-­‐narra;ve Le precisioni astrometriche In condizioni “normali” 1 arcsec Circa 0.01 arcsec Si possono raggiungere 0.001 arcsec E si punta a 100 µarcsec… Immagine non astrometrizzata Immagine astrometrizzata Nel “piccolo” anche il puntamento di precisione delle montature dei telescopi avviene usando un frame di stelle di riferimento piuEosto che basarsi sulla (necessariamente limitata) precisione meccanica dei cerchi di puntamento Esempio del soxware di puntamento T-­‐point Conclusione… e consolazione TuEo quello che avete visto oggi lo fanno i soxware … se sapete cosa calcolare, cosa significa, e a che vi serve!