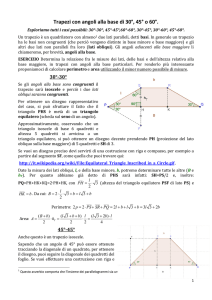
Testi tratti dal libro: ”Il nuovo pensiero geometrico” vol. 1, E. Cateni-R. Fortini-C. Bernardi, ed. Le Monnier
Problemi di geometria piana
1. La figura mostra un ottagono ottenuto costruendo su ogni
lato di un quadrato, ed esternamente ad esso, un triangolo
equilatero. Verificato che anche il quadrilatero ABCD è un
quadrato, se ne determini il perimetro sapendo che il
perimetro dell'ottagono è 12 m.
[R. 11,5... dopo aver approssimato le radici quadrate]
2. In un trapezio isoscele l'area è 204 m2, l'altezza è 12 m e il
perimetro 64 m. Calcolare le lunghezze dei lati.
[R. 26 m, 8 m, 15 m]
3. In un trapezio isoscele una diagonale, l'altezza e la base maggiore sono rispettivamente 119 cm,
56 cm e 112,5 cm. Determinare la base minore, il lato obliquo e l'area del trapezio.
[R. 97,5 cm, 56,5 cm, 5880 cm2]
4. In un triangolo isoscele la base e l'altezza sono uguali rispettivamente a 288 cm e 108 cm;
determinare le lunghezze delle altezze relative ai lati uguali.
[R. 172,8 cm]
5. Due lati di un triangolo sono lunghi rispettivamente 8 dm e 4,2 dm. Sapendo che l'altezza relativa
al primo lato è 63 cm, determinare l'altezza relativa al secondo lato.
[R. 12 dm]
6. Due lati consecutivi di un parallelogramma sono uguali a 12 m e 336 dm. Determinare le altezze
e l'area della figura sapendo che un suo angolo è di 30°.
[R. 60 dm e ....; 20160 dm2]
7. In un parallelogramma, un angolo alla base è di 30°; l'altezza è i 5/7 della base e la loro somma è
60 m. Calcolare i lati e l'area della figura.
[R. 35 m, 50 m, 875 m2]
8. Dividere un angolo di 72° in parti direttamente proporzionali ai numeri 7, 8 e 9.
[R. 21°, 24°, 27°]
9. Il perimetro di un triangolo isoscele è 580 m. Determinare il lato e la base del triangolo sapendo
che il loro rapporto è 8/13.
[R. 160 m, 260 m]
10. In un parallelogramma ABCD l'angolo BAD è di 60° e la diagonale minore BD è perpendicolare
al lato AB. Trovare i lati sapendo che i 3/5 del perimetro sono uguali a 1,44 m.
Suggerimento: indicare con x la lunghezza di AB...
[R. AB=0,4 m, AD=0,8 m]
11. Sono dati un segmento AB di lunghezza 10 cm ed un suo punto P. Dalla stessa parte di AB si
costruiscono i due quadrati APQR e PBMN nonché il rettangolo PMSR avente per dimensioni le
diagonali PR e PM dei due quadrati. Come deve essere scelto P affinché tale rettangolo abbia area
42 cm2?
Suggerimento: indicare con x la lunghezza di AP..
[R. due soluzioni, entrambe accettabili: AP=3cm, AP=7 cm]