scarica - Dipartimento di Fisica

Università degli Studi di Napoli “Federico II”
Scuola Politecnica e delle Scienze di Base
Area Didattica di Scienze Matematiche Fisiche e Naturali
Dipartimento di Fisica “Ettore Pancini”
Laurea triennale in Fisica
Tesi sperimentale
Calibrazione di un rivelatore a scintillatore
liquido con sorgenti radioattive
Relatori:
Candidato:
Prof. Giuliana Fiorillo
Dott. Biagio Rossi
Chiara Errico
Matricola N85/501
A.A. 2015/2016
Indice
Introduzione
3
1 Interazione radiazione-materia
1.1 Particelle cariche . . . . . . .
1.2 Fotoni . . . . . . . . . . . . .
1.2.1 Effetto fotoelettrico . .
1.2.2 Scattering Compton .
1.2.3 Produzione di coppie .
1.3 Meccanismi di scintillazione .
1.3.1 Scintillatori organici .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
5
5
6
7
8
10
11
12
2 Rivelazione di luce
2.1 Caratteristiche generali di un rivelatore
2.1.1 Sensibilità . . . . . . . . . . . .
2.1.2 Risposta temporale . . . . . . .
2.1.3 Pulse shape discrimination . . .
2.2 Risoluzione in energia . . . . . . . . . .
2.3 Caratterizzazione di un PMT . . . . .
2.4 Guadagno del PMT . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
15
15
16
16
17
18
19
21
3 Apparato sperimentale e analisi dei dati
3.1 Descrizione dell’apparato sperimentale .
3.2 Partitore di tensione del PMT . . . . . .
3.3 Misure di spettro di singolo fotone . . . .
3.4 Calibrazione del rivelatore . . . . . . . .
3.4.1 Linearità e risoluzione in energia
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
23
23
27
28
35
40
Conclusioni
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
44
2
Bibliografia
45
3
Introduzione
Lo scopo del presente lavoro di tesi è la calibrazione di un rivelatore a scintillatore liquido: l’EJ-309 della SCIONIX Holland che ha come solvente lo
Xilene. Questo rivelatore verrà utilizzato in esperimenti successivi per misurare l’energia in uscita di un fascio di neutroni incidenti su una TPC a
doppia fase ad Argon liquido.
I rivelatori a scintillazione, sono tra i rivelatori di particelle più usati e
diffusi nella fisica nucleare e delle particelle. Gli scintillatori sono rivelatori
che fanno uso della proprietà di alcuni materiali di emettere luce quando sono
colpiti da una particella. Solitamente questi scintillatori vengono accoppiati
ai fotomoltiplicatori che permettono di convertire la scintillazione in un impulso elettrico che può essere analizzato e fornire informazioni riguardo la
particella incidente.
Per effettuare la calibrazione del rivelatore a scintillatore liquido, sono
state utilizzante alcune sorgenti che emettono raggi gamma di energia nota.
Nel primo capitolo è descritta l’interazione della radiazione con la materia dando particolare rilievo all’interazione dei raggi gamma e soffermandosi
sugli spettri energetici attesi nel caso di effetto fotoelettrico e della diffusione Compton. Sono stati inoltre trattati i meccanismi di scintillazione
analizzando il caso degli scintillatori liquidi.
Le caratteristiche generali di un rivelatore quali la sensibilità, la risposta
temporale, la pulse shape discrimination e la risoluzione in energia sono state
trattate nel secondo capitolo. In questo capitolo è stato inoltre descritto il
funzionamento del fotomoltiplicatore, fondamentale in quanto accoppiato allo
scintillatore.
Nell’ultimo capitolo è stata riportata un accurata descrizione dell’apparato sperimentale utilizzato per la calibrazione dello scintillatore. È descritto il
lavoro svolto in laboratorio e l’analisi dei dati per ottenere i risultati necessari
alla calibrazione.
4
Capitolo 1
Interazione radiazione-materia
1.1
Particelle cariche
Il passaggio di particelle cariche attraverso la materia è caratterizzato da una
perdita di energia della particella e da una deflessione della particella rispetto
alla sua traiettoria originale. Questi effetti sono dovuti a due processi:
• collisioni inelastiche con gli elettroni atomici del materiale
• scattering elastico con i nuclei
Le prime sono responsabili della perdita di energia delle particelle cariche
pesanti, quest’energia è trasferita all’atomo causando ionizzazione ed eccitazione del mezzo. Le seconde permettono il trasferimento di poca energia
poiché le masse dei nuclei della maggior parte dei materiali sono generalmente
grandi rispetto a quelle delle particelle incidenti.
Le collisioni inelastiche sono per loro natura statistiche e poiché il numero
di queste collisioni lungo tutto il percorso è solitamente grande mentre la
fluttuazione dell’energia persa è piccola si può usare l’energia media persa
che prende il nome di stopping power).
per unità di lunghezza ( dE
dx
La perdita di energia per unità di lunghezza ad energie non relativistiche,
secondo la formula di Bethe-Bloch:
2
dE
2me γ 2 v 2 Wmax
C
2
2 Z z
2
−
ln
− 2β − δ − 2
= 2πNa re me c ρ
dx
A β2
I2
Z
Lo stopping power, come si può notare dalla figura 1.1, è dominato da un
fattore β12 e decresce all’aumentare dell’energia, fino a raggiungere il minimo
5
di ionizzazione (βγ ' 0.96c ). Successivamente vi è una risalita dovuta al
termine logaritmico.
Figura 1.1: Perdita di energia per unità di lunghezza in funzione dell’energia.
1.2
Fotoni
Il comportamento dei fotoni nella materia è totalmente diverso da quello delle
particelle cariche. La mancanza di carica elettrica da parte dei fotoni rende
impossibile le collisioni inelastiche con gli elettroni atomici che avvengono solo
per le particelle cariche. Le principali interazioni dei fotoni con la materia
sono:
a) effetto fotoelettrico
b) diffusione Compton
c) produzione di coppie
I fotoni sono molto più penetranti rispetto alle particelle cariche in quanto
la sezione d’urto dei tre processi è minore rispetto a quella delle collisioni
inelastiche degli elettroni. Inoltre, un fascio di fotoni, quando attraversa la
materia, non è degradato in energia ma solo attenuato in intensità. Il fotone
6
che interagisce con il materiale viene completamente rimosso dal fascio, o per
assorbimento o per scattering mentre i fotoni che riescono ad attraversare
il materiale sono quelli che non hanno avuto alcuna interazione e quindi
mantengono la stessa energia. Vi è quindi una riduzione rispetto al numero
iniziale di fotoni.
Figura 1.2: Sezione d’urto dei fotoni in funzione dell’energia: a) effetto
fotoelettrico, b) scattering Compton, c) produzione di coppie.
L’attenuazione del fascio di fotoni ha un andamento esponenziale che
dipende dallo spessore del materiale:
I(x) = I0 exp(−µx)
dove I0 è l’intensità del fascio incidente, x lo spessore del materiale e µ il
coefficiente di assorbimento che è una caratteristica del materiale.
Come si può vedere in figura 1.2 l’effetto fotoelettrico è predominante per
raggi γ a basse energie (fino alla centinaia di keV), la produzione di coppie
ad alte energie (5-10 MeV) e lo scattering Compton nel range di energia
compreso tra i precedenti.
1.2.1
Effetto fotoelettrico
L’effetto fotoelettrico è caratterizzato dall’assorbimento di un fotone da un
elettrone atomico che diviene pertanto libero come schematizzato nell’imma7
gine 1.3. Questo tipo di interazione non può avvenire con un elettrone libero
ma solo con quelli legati all’atomo.
Figura 1.3: Rappresentazione effetto fotoelettrico.
L’energia del elettrone emesso è data da:
E = hν − B.E.
dove B.E. rappresenta l’energia di legame dell’elettrone nella sua shell originaria, solitamente trascurabile per energie dell’ordine del keV.
La sezione d’urto dell’effetto fotoelettrico è proporzionale a Z 4 ÷ Z 5 e a
1
.
E 7/2
L’effetto fotoelettrico è il processo ideale nel caso in cui si sia interessati
a misurare l’energia del raggio γ incidente, in quanto si può assumere che
corrisponda all’energia cinetica dell’elettrone uscente. Durante il lavoro di
questa tesi si sono usate sorgenti radioattive γ monocromatiche di bassa
energia per calibrare il rivelatore tramite l’effetto fotoelettrico.
La distribuzione di energia attesa per eventi fotoelettrici è una gaussiana
con valore medio pari all’energia del fotone incidente come si può osservare
dalla figura 1.4.
1.2.2
Scattering Compton
Lo scattering Compton è probabilmente il processo meglio compreso tra quelli
che includono i fotoni ed è inoltre l’interazione predominante per i raggi γ
che hanno energie tipiche delle sorgenti radiative. In questo processo, il
8
Figura 1.4: Picco fotoelettrico.
fotone incide su un elettrone poco legato, che quindi appartiene alla shell più
esterna, e trasferisce parte dalla sua energia a quest’ultimo, come mostrato
in figura 1.5. Si verifica una deflessione del fotone, di un angolo θ, che si
forma tra la direzione del fotone incidente e quella dopo lo scattering; da
quest’angolo dipende l’energia trasferita all’elettrone.
Figura 1.5: Rappresentazione scattering Compton.
Applicando le leggi di conservazione dell’energia e del momento si ottiene
9
l’espressione che lega l’energia e l’angolo di scattering:
hν 0 =
dove γ =
hν
.
m0 c2
hν
1 + γ(1 − cos θ)
L’energia dell’elettrone è data da:
Ee− = hν − hν 0 = hν
γ(1 − cosθ)
1 + γ(1 − cosθ)
È possibile osservare due casi estremi: il primo in cui si ha θ ∼
= 0 e quindi
0 ∼
∼
dalle formule precedenti si ottiene hν = hν e Ee− = 0; il secondo rappresenta
una collisione head-on con θ ∼
= π alla quale corrisponde la massima energia
che può essere trasferita all’elettrone con un singolo scattering Compton.
La probabilità che avvenga lo scatering Compton dipende dal numero di elettroni disponibili per lo scattering sul bersaglio e quindi aumenta
linearmente con Z.
Nel caso dello scattering Compton, la distribuzione dell’energia dell’elettrone è rappresentata dal ”Compton continuum” e la massima energia
rilasciata corrisponde alla ”Compton edge”. Quest’ultima differisce di una
hν
dall’energia del raggio γ incidente.
quantità Ec = hν − Ee− |θ=π = 1+2γ
Figura 1.6: Spalla Compton.
1.2.3
Produzione di coppie
Il processo di produzione di coppie comporta la trasformazione di un fotone in
una coppia elettrone-positrone. Questo processo è energeticamente possibile
10
quando l’energia del fotone supera di due volte la massa a riposo dell’e−
(2m0 c2 = 1, 022MeV); tuttavia la probabilità che avvenga quest’interazione
resta molto bassa fin quando non si raggiungono energie di qualche MeV e
quindi questo processo è significativo solo ad alte energie.
Figura 1.7: Schema pair-production.
Nell’interazione il fotone scompare e tutta l’energia che possiede è trasformata in energia cinetica equamente divisa tra la coppia e− e+ .
1.3
Meccanismi di scintillazione
La rivelazione di radiazione ionizzante tramite la scintillazione prodotta da
alcuni materiali è uno dei metodi più antichi per la rivelazione di particelle
ed è a tutt’oggi uno dei metodi più utili per la rivelazione e la spettroscopia
di un vasto assortimento di radiazioni. Le proprietà che dovrebbe possedere
uno scintillatore ideale sono:
• convertire l’energia cinetica delle particelle incidenti in luce rivelabile
con un alta efficienza di scintillazione;
• la conversione dell’energia dovrebbe essere lineare affinché la luce emessa sia proporzionale all’energia depositata;
• il mezzo dovrebbe essere trasparente alla lunghezza d’onda della sua
stessa emissione in modo che ci sia una buona trasmissione di luce;
11
• il tempo di decadimento dovrebbe essere breve per far sı̀ che vengano
prodotti impulsi veloci;
• il materiale dovrebbe essere di buona qualità e abbastanza grande per
poter essere utilizzato come rivelatore;
• il suo indice di rifrazione dovrebbe essere prossimo a quello del vetro in modo da poter accoppiare efficientemente lo scintillatore ad un
rivelatore di luce (solitamente fotomoltiplicatori).
Non esistono materiali che verifichino simultaneamente queste proprietà
e per questo motivo la scelta del rivelatore è un compromesso tra questi ed
altri fattori.
Esistono due tipi di scintillatori:
• gli inorganici che hanno la maggiore luce in uscita ed una risposta
lineare ma, sono relativamente lenti nel loro tempo di risposta
• gli organici che sono più veloci, hanno un tempo di decadimento dell’
ordine dei ns, ma producono meno luce.
L’alto valore di Z e della densità dei cristalli inorganici li rendono una
scelta migliore per la rivelazione di raggi γ, mentre gli organici sono preferiti,
per il loro contenuto di idrogeno, per la spettroscopia β e la rivelazione di
neutroni veloci.
Esistono diversi processi di scintillazione che possono essere distinti. La
fluorescenza è l’emissione pronta di radiazione visibile da una sostanza dopo
la sua eccitazione; la fosforescenza corrisponde all’emissione di lunghezze
d’onda maggiori rispetto alla fluorescenza ma con un ritardo temporale che
è solitamente molto più elevato; la fluorescenza ritardata appare nello stesso
spettro di emissione della fluorescenza ma con un ritardo ancor più alto dopo
l’eccitazione.
1.3.1
Scintillatori organici
Gli scintillatori organici sono composti di idrocarburi aromatici contenenti
strutture di anelli benzenici. La loro peculiarità è un tempo di decadimento
di pochi nanosecondi o anche meno. La scintillazione in questo caso è data
dalla transizione dell’elettrone di valenza libero della molecola. In figura 1.8
è riportato un diagramma energetico nel quale è possibile distinguere gli stati
12
Figura 1.8: Diagramma dei livelli energetici di uno scintillatore organico.
di singoletto (S ) da quelli di tripletto (T ). Lo stato fondamentale è S0 al di
sopra del quale vi sono gli stati eccitati S1 , S2 , lo stato più basso di tripletto
è T0 al quale corrispondono gli stati eccitati T1 , T2 . Inoltre associata ad ogni
livello elettronico vi è una struttura che corrisponde a modi di eccitazione
vibrazionali della molecola che in figura 1.8 sono rappresentati con le linee
tratteggiate. L’energia tra i diversi livelli è dell’ordine dell’eV mentre quella
che corrisponde ai livelli vibrazionali è dei decimi di eV.
L’energia dovuta alla radiazione incidente, eccita entrambi i livelli, sia
quello elettronico che quello vibrazionale. Lo stato S2 decade, in un tempo
minore di 10 ps, senza emissione di radiazione in S1 (decadimento interno).
C’è invece un’ alta probabilità di decadimento radiativo in uno degli stati
vibrazionali di S0 con un tempo dell’ordine dei ns. Questo è il processo della
fluorescenza che è descritto dalla componente veloce. Gli stati di tripletto
decadono per degradazione interna in T0 che, a causa delle regole di selezione,
non può decadere nello stato S0 . Il meccanismo di diseccitazione avviene
13
medianta l’interazione con un altro stato T0 : T0 + T0 = S1 + S0 + f otoni.
Questo processo è invece descritto dalla componente lenta.
Scintillatori liquidi
Lo scintillatore calibrato in questo lavoro di tesi è uno scintillatore liquido.
Gli scintillatori liquidi sono una soluzione di uno o più scintillatori organici
ed il processo di scintillazione è equivalente a quello descritto in precedenza,
mentre il meccanismo di assorbimento dell’energia è differente.
In questi scintillatori, l’energia di viene assorbita prima dal solvente e
poi passa al soluto; questo processo avviene molto rapidamente. L’efficienza
di scintillazione aumenta con la concentrazione di soluto e le concentrazioni
tipiche sono di 3g di soluto per litro di solvente.
La risposta di questi scintillatori è veloce con tempi di decadimento dell’ordine di (3 ÷ 4)ns. Sono inoltre molto vantaggiosi perché facilmente collegabili con altri materiali in modo da aumentarne l’efficienza. Tuttavia
quest’unione provoca un allungamento del tempo di decadimento ed una diminuzione della luce in uscita dovuta agli effetti di quenching. Un aspetto
negativo degli scintillatori liquidi è una grande sensibilità alle impurità, è
infatti possibile osservare, da due campioni, impulsi notevolmente differenti.
14
Capitolo 2
Rivelazione di luce
2.1
Caratteristiche generali di un rivelatore
Esistono diversi tipi di rivelatori le cui caratteristiche fondamentali sono:
• sensibilità;
• risposta temporale;
• risoluzione temporale;
• risoluzione in energia;
• efficienza.
È praticamente impossibile costruire un rivelatore che risulti eccellente in
tutte le sue caratteristiche. Per tale motivo, si seleziona il rivelatore che
meglio soddisfa le esigenze di una particolare misura.
In questo lavoro di tesi si è utilizzato un rivelatore a scintillatore liquido.
I meccansimi di scintillazione di questo tipo di rivelatori sono stati trattati
nel capitolo precedente. Le principali caratteristiche degli scintillatori sono
la sensibilità all’energia ossia la capacità di rispondere in maniera lineare
all’energia rilasciata, un tempo di risposta rapido rispetto ad altri tipi di
rivelatori e la ”pulse shape discrimination” che permette la distinzione delle
particelle attraverso l’analisi degli impulsi in uscita. Queste caratteristiche
saranno descritte in modo più completo nei prossimi paragrafi.
15
2.1.1
Sensibilità
La sensibilità è la capacità di produrre un segnale per una data energia
o radiazione. Si può assumere con buona approssimazione che vi sia una
proporzionalità diretta tra la luce emessa e l’energia. In realtà la risposta
degli scintillatori è più complessa e dipende anche dal tipo di particella e dalla
densità di ionizzazione. In particolare le particelle più pesanti mostrano una
deviazione più marcata ad energie più basse rispetto agli elettroni.
La risposta degli scintillatori organici può essere ben descritta da una
e l’energia persa
relazione tra la fluorescenza emessa per unità di lunghezza dL
dx
).
Il
modello
semi-empirico
dalla particella carica per unità di lunghezza ( dE
dx
utilizzato è quello di Birks:
S dE
dL
dx
=
dx
1 + kB dE
dx
supponendo che la densità delle molecole eccitate sia direttamente proporzionale alla densità di ionizzazione e supponendo inoltre che in assenza di quenching, che è il fenomeno attraverso il quale viene smorzata la fluorescenza, la
luce prodotta sia proporzionale all’energia persa si ottiene:
dL
dE
=S
dx
dx
dove S è l’efficienza di scintillazione, cioè quanta energia viene trasformata
in luce.
2.1.2
Risposta temporale
L’evoluzione temporale del processo di emissione può essere descritto, in
prima approssimazione come un decadimento esponenziale
N=
N0
−t
exp
τd
τd
dove τd è la costante di decadimento e N0 è il numero totale di fotoni emessi.
Per descrivere in modo completo il comportamento degli scintillatori è necessario utilizzare un modello della dipendenza temporale della scintillazione
prodotta che tenga conto di due componenti: una veloce che rappresenta
16
Figura 2.1: Rappresentazione delle due componenti di decadimento e della
curva totale del decadimento.
la fluorescenza ed una lenta dovuta alla fosforescenza ed alla fluorescenza
ritardata. In questo caso si otterrà:
N = A exp
−t
−t
+ B exp
τf
τs
dove τf è la costante di decadimento veloce (fast) e τs è la costante di decadimento lenta (slow). In figura 2.1 sono mostrate la componente lenta, quella
veloce e l’andamento totale del decadimento.
2.1.3
Pulse shape discrimination
Per la maggioranza degli scintillatori organici la fluorescenza rappresenta la
maggior parte della luce emessa; spesso, però, è possibile osservare un’altra
componente che corrisponde alla fluorescenza ritardata. La curva prodotta può essere rappresentata dalla somma dei due decadimenti esponenziali
come visto nel paragrafo 2.1.2. Se la componente veloce ha un tempo di
decadimento di pochi nanosecondi, la componente lenta avrà un tempo di
decadimento di centinaia di nanosecondi. Un’importante conseguenza è che
la frazione di luce che appare nella componente lenta dipende dalla natura
della particella eccitante, in particolare dalla densità di ionizzazione. È possibile utilizzare questa dipendenza per distinguere le particelle nel rivelatore.
Questo è il processo della pulse shape discrimination che permette di distinguere le diverse particelle che attraversano il rivelatore, osservando la forma
17
Figura 2.2: Risposta temporale che mette in evidenza la differenza tra le
diverse radiazioni.
dell’impulso emesso. Questo metodo è ampiamente utilizzato in particolar
modo per distinguere i raggi γ dai neutroni come è possibile osservare in
figura 2.2.
2.2
Risoluzione in energia
Una caratteristica di fondamentale importanza per i rivelatori che sono progettati per misurare l’energia della radiazione incidente è la risoluzione in
energia. Questa solitamente può essere misurata osservando l’impulso in
uscita ottenuto da un fascio monoenergetico inviato sul rivelatore. Ciò che ci
si aspetta è una delta ma, a causa delle fluttuazioni nel numero di ionizzazioni ed eccitazioni, si osserva una gaussiana. Per questo motivo la risoluzione
viene solitamente calcolata in termini di ampiezza a mezza altezza
√
∆E = 2σE 2ln2 = 2.35σE
La risoluzione R relativa all’energia E è data da:
R=
∆E
E
18
La risoluzione viene solitamente espressa in percentuale ed è una funzione
dell’energia rilasciata nel rivelatore. L’energia media necessaria per produrre
sia una ionizzazione sia l’eccitazione che da luogo alla scintillazione è una
quantità fissata (w) e dipende dal materiale. Per un’energia E ci si aspetta
in media J = E
ionizzazioni; all’aumentare dell’energia c’è quindi un aumenw
to del numero di ionizzazioni. Il numero di ionizzazioni prodotte segue la
statistica di Poisson, la varianza è σ 2 = J e quindi la risoluzione è:
√
J
σ
R = 2.35 = 2.35
J
J
Nel caso degli scintillatori la risoluzione è data da
r
w
R = 2.35
E
ed è quindi inversamente proporzionale alla radice quadrata dell’energia.
In aggiunta alle fluttuazioni dovute al rilascio di energia, c’è un insieme di fattori esterni che può modificare la risoluzione totale del rivelatore. Di questi fattori fa parte il rumore dovuto all’elettronica. Assumendo che tutte queste sorgenti siano indipendenti ed abbiano una distribuzione gaussiana, la risoluzione totale è data dalla somma in quadratura:
(∆E)2 = (∆Erivelatore )2 + (∆Eelettronica )2 .
2.3
Caratterizzazione di un PMT
Il diffuso uso degli scintillatori come rivelatori non sarebbe stato possibile
senza un dispositivo che fosse capace di convertire una debole luce in un
impulso elettrico da poter analizzare. Il fotomoltiplicatore è un dispositivo
che converte la luce in un segnale elettrico che viene accoppiato agli scintillatori e che compie questo lavoro senza l’aggiunta di una grande quantità di
rumore al segnale prodotto. Esistono diversi tipi di PMT che sono sensibili
a lunghezze d’onda nell’ultravioletto, visibile ed infrarosso che hanno diverse
applicazioni nella spettroscopia ottica, misurazioni laser e astronomia.
La struttura del fotomoltiplicatore è rappresentata in figura 2.3; questo è
caratterizzato da un catodo fotosensibile che permette di trasformare i fotoni
incidenti in elettroni, seguito da un sistema di raccolta, per portarli senza
perdite al primo stadio di moltiplicazione, da una sezione moltiplicatrice formata da dinodi posti a ddp costante ed infine da un anodo che collegato
all’elettronica ci consente di analizzare il segnale.
19
Figura 2.3: Struttura di un PMT.
Il fotocatodo converte la luce incidente in elettroni tramite l’effetto fotoelettrico; per facilitare il passaggio della luce, il materiale fotosensibile è disposto in una lamina sottile all’interno della finestra del PMT che è solitamente
costituita di vetro o quarzo. Una grandezza di fondamentale importanza è
la quantum efficiency (QE) del fotocatodo che è definita come:
η(λ) =
numero di f otoelettroni emessi
numero di f otoni incidenti sul catodo
La QE sarebbe del 100% per un fotocatodo ideale. La maggior parte dei
fotocatodi moderni è costituita da semiconduttori con i quali si riesce a raggiungere una QE del 20% − 30%, nel caso degli SBA e UBA anche ben oltre
il 45%.
Dopo l’emissione dal fotocatodo gli elettroni devono essere raccolti e focalizzati nel primo stadio della sezione moltiplicatrice. Questo è ottenuto
tramite l’utilizzo di un campo elettrico in una configurazione particolare. Ci
sono due caratteristiche fondamentali che devono essere soddisfatte:
20
• La raccolta deve essere la più efficiente possibile, per esempio il maggior numero possibile di elettroni emessi deve raggiungere la sezione
moltiplicatrice indipendentemente dal punto d’origine sul catodo
• il tempo che l’elettrone impiega a raggiungere il primo dinodo deve
essere il più indipendente possibile dal punto di emissione.
La sezione moltiplicatrice amplifica la debole corrente primaria utilizzando una serie di emissioni secondarie per produrre una corrente misurabile
all’anodo. Gli elettroni provenienti dal fotocatodo sono accelerati dal campo
elettrico e costretti a colpire la superficie di un elettrodo chiamata dinodo.
I dinodi sono costruiti con un materiale opportuno in modo tale che l’energia dell’elettrone incidente produca la ri-emissione di più di un elettrone
dalla stessa superficie. Il processo di emissione secondaria è simile alla fotoemissione eccetto per il fatto che il fotone è ora sostituito da un elettrone.
L’energia dell’elettrone incidente viene trasferita agli elettroni presenti nel
dinodo permettendo ad un determinato numero di elettroni secondari di lasciare il materiale. Il guadagno di ogni elettrodo è conosciuto come fattore
di emissione secondaria δ:
δ=
numero di elettroni secondari emessi
numero di elettroni incidenti primari
Un buon dinodo dovrebbe avere le seguenti caratteristiche:
• un grande fattore di emissione secondaria
• stabilità di emissione secondaria anche ad alte correnti
• basso rumore
2.4
Guadagno del PMT
L’amplificazione totale o il guadagno di un PMT dipende dal numero di
dinodi nella sezione moltiplicatrice e dal fattore di emissione secondaria δ,
che è una funzione dell’energia dell’elettrone primario. Nella sezione moltiplicatrice, l’energia dell’elettrone incidente è chiaramente una funzione della
differenza di potenziale tra i dinodi. Possiamo infatti scrivere:
δ = KVd
21
Assumendo che il potenziale applicato sia diviso equamente tra i dinodi, il
guadagno totale del PMT è
G = δ n = (KVd )n
dove n è il numero degli stadi.
È molto importante che ci sia una stabilità nella tensione applicata, il
metodo maggiormente utilizzato è la combinazione di uno stabilizzatore di
alta tensione con un partitore di tensione.
Il partitore è caratterizzato da una catena di resistenze scelte in modo da
poter applicare la tensione opportuna ad ogni dinodo.
22
Capitolo 3
Apparato sperimentale e analisi
dei dati
3.1
Descrizione dell’apparato sperimentale
Figura 3.1: Schema dell’apparato sperimentale.
L’apparato sperimentale utilizzato è composto da uno scintillatore liquido
accoppiato ad un fotomoltiplicatore ed è mostrato in figura 3.6. Lo scintillatore liquido è l’EJ-309 della SCIONIX Holland che fa parte di quella classe
di scintillatori che ha come solvente lo Xilene. Possiede un certo numero
23
di proprietà che lo rendono ideale per la rivelazione di raggi γ e neutroni
con energie dell’ordine del MeV. Queste proprietà, mostrate in figura 3.2,
includono: un’efficienza di scintillazione di 12300 fotoni/MeV, un tempo di
risposta di 3.5 ns, e lunghezza d’onda di massima emissione di 424 nm (come
mostrato in figura 3.4).
Figura 3.2: Specifiche dello scintillatore liquido EJ-309.
Il fotomoltiplicatore è il modello 9821B della ET Enterprises, le cui caratteristiche sono mostrate in figura 3.5. La finestra piano-concava del fotomoltiplicatore ha un diametro di 78 millimetri ed una sensibilità alle lunghezze
d’onda blu-verde [λ ' (400 ÷ 500)nm]. La sezione moltiplicatrice è formata
da 12 dinodi di una lega di rame e berillio (BeCu) progettati con una focalizzazione lineare per ottenere una buona risposta temporale e linearità.
In figura 3.3 è riportata la quantum efficiency del fotocatodo ed è possibile
notare un massimo del 30% proprio in corrispondenza delle lunghezze d’onda
blu.
La configurazione utilizzata per la presa dati descritta in questa tesi è
schematicamente riportata in figura 3.1. Il fotocatodo del PMT è collegato
24
Figura 3.3: Quantum efficiency del PMT 9821B della ET enterprises.
Figura 3.4: Spettro di emissione dello scintillatore liquido EJ-309.
all’alta tensione (che non può essere superiore ai 2900 V), mentre il segnale
che arriva all’anodo è connesso ad un amplificatore che ha due canali in uscita Ch0 e Ch1 con amplificazione rispettivamente ×10 e ×1. Tali canali sono
collegati a loro volta all’ADC, che campiona il segnale analogico trasformandolo in digitale. L’ADC salva i dati convertiti su una memoria interna che
viene letta dal PC e salvata su disco, in presenza di un segnale di trigger.
25
Figura 3.5: Caratteristiche del PMT 9821B della ET Enterprises.
26
L’ADC adoperato è il modello V1720 prodotto dalla CAEN che ha 12 bit di
risoluzione e 4 ns di campionamento ed è mostrato in figura 3.7. Un’ulteriore
uscita dell’amplificatore è collegata all’oscilloscopio in modo da permetterci
di monitorare visivamente l’impulso.
Figura 3.6: Rivelatore a scintillatore liquido accoppiato al PMT 9821B della
ET Enterprises.
3.2
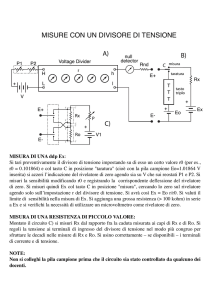
Partitore di tensione del PMT
Con la configurazione descritta nel paragrafo 3.1, è stato possibile in primo luogo calcolare la somma di tutte le resistenze del partitore di tensione
presente nella sezione moltiplicatrice del PMT. La tensione è stata variata
tramite il generatore NIM della CAEN N1470, mostrato in figura 3.8, in un
intervallo che va da 0 V a 2200 V, ed è stata monitorata la corrente che
scorreva nel partitore di tensione. I valori sono riportati in tabella 3.1.
L’andamento dei dati sperimentali segue la prima legge di Ohm V =
iR. In figura 3.9 è rappresento l’andamento della tensione in funzione della
corrente. Per ogni valore è stato considerato un errore dell’ 1%. Effettuando
un fit lineare dei punti, l’inverso del coefficiente angolare della retta ci fornisce
il valore
R = (2.422 ± 0.007) MΩ
27
Figura 3.7: Fotografia del sistema di acquisizione: ADC V1720 della CAEN
e amplificatore costruito dal laboratorio di elettronica di INFN-LNGS.
3.3
Misure di spettro di singolo fotone
Idealmente, la sezione moltiplicatrice dovrebbe fornire un guadagno costante,
ma ciò non è possibile a causa della natura statistica delle emissioni secondarie. I singoli elettroni aventi la stessa energia produrranno per questo motivo
un numero diverso di elettroni secondari, provocando cosı̀ una variazione nel
guadagno. Una stima delle fluttuazioni nel guadagno della catena moltiplicatrice è data dallo spettro di singolo elettrone, che è la distribuzione di carica
degli impulsi di risposta ad un singolo fotone, in uscita dal PMT. È proprio
per la natura statistica delle emissioni che l’impulso in uscita sarà diverso
per ogni evento di singolo elettrone.
28
VP M T [V ]
9.0
19.0
49.0
99.2
199.2
299.4
399.4
499.4
599.6
I [µA]
2.55
6.70
19.00
39.50
80.75
122.05
163.30
204.55
245.85
VP M T [V ]
699.6
799.4
899.6
999.6
1099.8
1198.8
1300.0
1400.0
1499.6
I [µA]
287.10
328.46
369.85
411.25
452.70
494.15
535.60
577.15
618.60
VP M T [V ]
1599.8
1699.8
1800.0
1899.8
1999.8
2049.8
2100.0
2150.0
2199.8
I [µA]
660.15
701.65
743.40
785.00
826.60
847.50
868.40
889.20
909.95
Tabella 3.1: Riassunto dei valori di corrente e tensione del partitore di
tensione.
L’ADC è collegato ad una scheda PCI installata in un computer mediante
due fibre ottiche che permettono ai due apparecchi di comunicare. Per le
misure di singolo fotoelettrone, si è impostata una soglia di trigger sul canale
Ch0 dell’ADC (quello con amplificazione ×10) a circa 1 mV sopra il livello
medio di rumore elettronico. All’arrivo del trigger, il PC salva su disco il
buffer di memoria dell’ADC preimpostato a 1500 campionamenti [da −2 µs
a +4 µs]. I dati sono suddivisi in RUN contenenti 200000 eventi, ognuno con
una diversa tensione di alimentazione [da 1800 V a 2200 V] i cui valori sono
riportati in tabella 3.2.
In figura 3.10 è mostrato un impulso tipico ed è possibile notare in nero
quello amplificato ed in rosso quello senza amplificazione. Ognuno di questi
impulsi è stato integrato da −0.02 µs a 0.02 µs (intervallo evidenziato in verde
in figura 3.10) in modo da poter ottenere la carica del singolo fotoelettrone
(SPE) come:
Z
Z
∆V
dt
Q = Idt =
R
con R = 50Ω.
Mediante un programma opportunamente creato, i risultati dell’integrazione sono stati riportati in un istogramma (vedi figura 3.11) per diversi
valori di tensione nell’intervallo che va da 1800 V a 2200 V. È stata effettuata una conversione da ADCcount × sample a mV × ns, per poter avere
29
Figura 3.8: Generatore NIM della CAEN e amplificatore.
negli istogrammi i valori della carica in pC, usando la seguente formula:
mV × ns =
ADCcount × sample
0.5 × 4
Il picco di singolo fotoelettrone in ogni istogramma, riportati nelle figure
3.11, 3.12, 3.13, è stato fittato con una gaussiana:
(x−µ)2
1
f (x) = √ e− 2σ2
σ 2π
il cui valor medio (µ) ci restituisce il valore della carica corrispondente ad un
fotone. I valori medi della carica ottenuti sono riportati nella tabella 3.3 in
funzione delle diverse tensioni di alimentazione e dei RUN corrispondenti, ed
aumentano in funzione della tensione come atteso.
30
Figura 3.9: Andamento della tensione in funzione della corrente che scorre
nel partitore del PMT.
RUN
6149
6150
6151
6153
6148
6152
6154
6155
6156
VP M T [V ]
1800
1850
1900
1950
2000
2050
2100
2150
2200
Tabella 3.2: RUN di acquisizione degli eventi di singolo fotoelettrone
corrispondenti a tensioni di alimentazioni diverse.
31
Figura 3.10: Impulso di singolo fotoelettrone. In nero il segnale del Ch0
amplificato ed in rosso quello del Ch1 non amplificato.
Figura 3.11: Spettro di singolo fotoelettrone alla tensione di 2200 V.
Il guadagno del PMT si ottiene dividendo la risposta ottenuta per un
singolo fotoelettrone emesso dal fotocatodo per la carica dell’elettrone (e− =
1.602 × 10−19 ). I risultati ottenuti sono riportati in tabella 3.3. Il guadagno
è stato graficato in funzione della tensione di alimentazione, anche in scala
bilogaritmica. Gli andamenti sono mostrati in figura 3.14. È stato eseguito il
fit dei punti sperimentali, con l’approssimazione che la tensione applicata sia
equamente divisa tra tutti i dinodi. Il guadagno risulta essere proporzionale
32
(a) SPE alla tensione di 1800 V.
(b) SPE alla tensione di 1850 V.
(c) SPE alla tensione di 1900 V.
(d) SPE alla tensione di 1950 V.
(e) SPE alla tensione di 2000 V.
(f) SPE alla tensione di 2050 V.
Figura 3.12: SPE a diverse tensioni.
33
(a) SPE alla tensione di 2100 V.
(b) SPE alla tensione di 2150 V.
Figura 3.13: Spettri di singolo fotoelettrone a diverse tensioni.
a V CN dove V è la tensione applicata al PMT, N il numero di stadi e C
un parametro che dipende dal materiale e dalla struttura dei dinodi ed è
compreso tra 0.7 e 0.8. L’andamento che si ottiene è quello atteso ed i
parametri del fit sono: K = 7.02 × 10−25 ± 1.01 × 10−24 , N = 12.06 ± 0.3
che è il numero di dinodi e C = 0.754 ± 0.019 che rientra nei limiti del valore
atteso.
RUN
6149
6150
6151
6153
6148
6152
6154
6155
6156
VP M T [V ]
1800
1850
1900
1950
2000
2050
2100
2150
2200
Q [pC]
0.435 ± 0.011
0.603 ± 0.017
0.728 ± 0.015
0.970 ± 0.018
1.21 ± 0.03
1.47 ± 0.03
1.83 ± 0.04
2.27 ± 0.08
2.79 ± 0.05
Guadagno
(2.72 ± 0.07) × 106
(3.77 ± 0.11) × 106
(4.55 ± 0.09) × 106
(6.05 ± 0.12) × 106
(7.57 ± 0.16) × 106
(9.16 ± 0.18) × 106
(1.14 ± 0.03) × 107
(1.42 ± 0.05) × 107
(1.74 ± 0.03) × 107
Tabella 3.3: Valori medi della carica ricavati dagli spettri di singolo fotoelettrone per i diversi valori di tensione e valori del guadagno del PMT ottenuti
dalla conversione della carica.
34
(a)
(b)
Figura 3.14: Andamento del guadagno in funzione della tensione graficato
anche in scala bilogaritmica (b).
3.4
Calibrazione del rivelatore
Figura 3.15: Schema dell’apparato sperimentale con sorgente radioattiva.
Durante il mio lavoro di tesi ho effettuato una calibrazione del rivelatore
a scintillatore liquido, utilizzando alcune sorgenti che emettono raggi gamma
di energia nota. Le sorgenti utilizzate sono riportate in tabella 3.4 in modo
35
da poter stabilire una relazione tra energia in keV e la risposta del rivelatore
in termini di fotoelettroni.
Lo schema dell’apparato sperimentale utilizzato per tali misure è mostrato
in figura 3.15. Sono stati acquisiti dati a turno con le diverse sorgenti. La
catena di acquisizione è la stessa descritta nel paragrafo 3.1. Le sorgenti,
contenute in appositi supporti di materiale plastico dal diametro di circa
3 cm sono state adagiate a contatto con la parete esterna del rivelatore a
scintillatore liquido, al centro dello stesso. La sola sorgente di americio,
più attiva delle altre, è stata posizionata 4 cm distante dal rivelatore per
minimizzare il numero di eventi multipli.
I dati acquisiti con le sorgenti gamma sono stati suddivisi in RUN contenenti 500000 eventi per ogni sorgente. L’ADC utilizzato è lo stesso descritto
nel paragrafo 3.1. La soglia del trigger è stata impostata ad un valore maggiore di 10 fotoelettroni equivalenti per massimizzare il numero di eventi
interessanti per la calibrazione. Si è scelto lo stesso valore della soglia di
trigger per tutte le sorgenti.
In tabella 3.4 sono riportate le energie dei raggi gamma corrispondenti
alle diverse sorgenti radioattive, la tensione di alimentazione del PMT ed i
RUN corrispondenti. Per ogni RUN sono stati acquisiti gli eventi sia con
amplificazione ×10 che senza amplificazione.
Per l’analisi dati delle sorgenti meno energetiche (210 P b e 241 Am) ho considerato il canale con l’amplificazione. Le sorgenti più energetiche, presentavano una saturazione dell’elettronica, di conseguenza per le sorgenti di 133 Ba e
137
Cs, si è utilizzato il canale non amplificato per l’analisi dati. Inoltre, molti
degli eventi di 60 Co (la sorgente più energetica utilizzata) saturavano l’elettronica. Si è quindi scelto di diminuire il guadagno del PMT alimentandolo
a 1800 V invece che a 2000 V.
RUN
6161
6160
6163
6162
6165
HP M T [V ]
2000
2000
2000
2000
1800
Amplificazione
×10 Ch0
×10 Ch0
×1 Ch1
×1 Ch1
×1 Ch1
Source
210
Pb
241
Am
133
Ba
137
Cs
60
Co
γ Energy [keV]
47
60
356
661.64
1173.2
Tabella 3.4: Energia dei raggi gamma per le varie sorgenti.
36
Sono stati inoltre acquisiti due RUN da 500000 eventi di radiazione di
fondo del laboratorio (background) per le diverse configurazioni di presa dati
sopraelencate, ovvero per i due canali di amplificazione e per le due tensioni
di alimentazione del PMT, mantenendo la soglia del trigger costante in modo
da poterli sottrarre ai RUN acquisiti con la sorgente.
BG
BG
RUN
6164
6168
HP M T [V ]
2000
1800
Tabella 3.5: Background alle tensioni di acquisizione con sorgenti.
In figura 3.16 (a) è mostrata una forma d’onda tipica di scintillazione di un
evento acquisito con la sorgente di 60 Co ed in figura 3.16 (b) è rappresentato
un suo ingrandimento che ci permette di distinguere la componente veloce e
quella lenta della scintillazione. In entrambe le figure in nero è rappresentato
il segnale amplificato ed in rosso quello non amplificato.
Impulsi analoghi sono stati ottenuti per tutte le sorgenti utilizzate. Ognuno di questi impulsi è stato integrato da −0.03 µs a 1 µs in modo da ricostruire la carica ottenuta per ogni singolo evento. Come nel paragrafo 3.3,
è stata effettuata una conversione da ADCcount × sample a mV × ns. Per
ottenere il numero di fotoelettroni il risultato ottenuto dall’integrazione è
stato diviso per la carica corrispondente ad un singolo fotone, calcolata nel
paragrafo 3.3. Per i RUN delle sorgenti di 210 P b, 241 Am, 133 Ba e 137 Cs il
valore del singolo fotoelettrone è 1.21 pC, invece per il RUN della sorgente
di 60 Co il valore del singolo fotoelettrone è 0.435 pC.
Lo spettro in energia per le diverse sorgenti è stato riportato in un istogramma come mostrato nelle figure 3.17, 3.18 e 3.19. In nero è rappresentato
lo spettro in presenza della sorgente, in blu il background ed in rosso la
differenza tra i due. In figura 3.17 (a) riporto lo spettro di energia della
sorgente di 210 P b. Si vede chiaramente il picco fotoelettrico attorno ai 110
fotoelettroni. Del picco fotoelettrico è stato effettuato un fit gaussiano che
restituisce: # f otoelettroni = 114.6 ± 0.1 e σ = 20.37 ± 0.19. In figura 3.17
(b) è riportato lo spettro di energia della sorgente di 241 Am ed è stato fatto
un ragionamento analogo al precedente. I valori ottenuti dal fit gaussiano
sono: # f otoelettroni = 153.5 ± 0.1 e σ = 22.39 ± 0.13.
37
(a) Forma d’onda tipica di scintillazione di un evento acquisito durante il RUN
con la sorgente di Cobalto.
(b) Ingrandimento della forma d’onda tipica di scintillazione di un evento
acquisito durante il RUN con la sorgente di Cobalto.
Figura 3.16: Forma d’onda tipica di scintillazione di un evento acquisito
durante il RUN con la sorgente del Cobalto (a) ed un suo ingrandimento
che ci permette di notare la componente veloce della scintillazione e i fotoni
ritardati della componente lenta (b). In nero il segnale amplificato del Ch0
ed in rosso quello del Ch1 non amplificato.
38
(a) Spettro ottenuto con
210
P b.
(b) Spettro ottenuto con
241
Am.
Figura 3.17: Spettri ottenuti con le sorgenti radioattive meno energetiche (a)
45 keV, (b) 60 keV.
(a) Spettro ottenuto con
133
Ba.
(b) Spettro ottenuto con
(c) Spettro ottenuto con
60
137
Cs.
Co.
Figura 3.18: Spettri ottenuti con le sorgenti radioattive più energetiche (a)
356 keV, (b) 661.64 keV, (c) 1332.5 keV.
39
(a) Ingrandimento dello spettro ottenuto (b) Ingrandimento dello spettro ottenuto
con 133 Ba.
con 137 Cs.
Figura 3.19: Ingrandimento degli spettri ottenuti con le sorgenti (a) 133 Ba,
(b) 137 Cs considerando il picco fotoelettrico rispettivamente alle energie di
(a) 31 keV e (b) 32.3 keV.
In figura 3.18 sono riportati i tre spettri in energia relativi alle sorgenti di
(a) 133 Ba, (b) 137 Cs e (c) 60 Co. In questo caso l’energia rilasciata dalle sorgenti è tale da permetterci di osservare la spettro Compton ma non un chiaro
picco fotoelettrico. Si è scelto di utilizzare il valore della spalla Compton come punto di calibrazione. Teoricamente il ”Compton continuum” termina in
corrispondenza della massima energia Compton con una spalla ripida come
mostrato in figura 1.6. In realtà, come si osserva nelle figure 3.18, la spalla
Compton presenta una coda gaussiana dovuta alla risoluzione non infinita
del rivelatore. Per questo motivo si è scelto di effettuare un fit gaussiano in
corrispondenza della spalla per poter ottenere sia l’energia rilasciata che la
risoluzione. Per le sorgenti di 133 Ba e 137 Cs, è stato effettuato il fit anche
del picco fotoelettrico, che è stato notato mediante un ingrandimento dello
spettro energetico delle due sorgenti ed è mostrato in figura 3.19, le energie
in questo caso sono di 31 keV e 32.3 keV I risultati del fit oltre ad essere
riportati nei grafici, sono riportati in tabella 3.6.
3.4.1
Linearità e risoluzione in energia
La curva di calibrazione, mostrata in figura 3.20, è stata ottenuta graficando
i valori riportati in tabella 3.6. Si può notare dall’andamento dei punti sperimentali graficati che vi è una risposta lineare della resa in luce in funzione dell’energia. La resa in luce (LY Light-Yeld) è una caratteristica fondamentale
40
RUN
6163
6162
6161
6160
6163
6162
6165
Source
133
Ba
137
Cs
210
Pb
241
Am
133
Ba
137
Cs
60
Co
γ Energy [keV]
31
32.3
47
60
356
661.64
1332.5
Ee− [keV ]
208.96
479.9
1121.6
#P E
68.86 ± 0.11
76.51 ± 0.3
114.6 ± 0.1
153.5 ± 0.1
491.4 ± 1.2
1334 ± 3
2904 ± 4
σ
19.74 ± 0.14
24.88 ± 0.14
20.37 ± 0.19
22.39 ± 0.13
108.4 ± 0.6
128 ± 3
351.4 ± 9
Tabella 3.6: Energia dei raggi gamma per le varie sorgenti, risultati ottenuti
dai fit e Ec = hν − Ee− |θ=π
dei rivelatori ed è il numero di fotoni emessi per energia rilasciata.
# f otoni prodotti
LY =
E
Un valore della resa in luce dello scintillatore è quindi ottenuto dalla pen-
Figura 3.20: Linearità della resa in luce in funzione dell’energia.
denza del grafico 3.20 che risulta essere:
LY = (2.589 ± 0.035)
41
γ
keV
È stata effettuata la propagazione degli erori sul numero di fotoelettroni,
in quanto non era sufficiente considerare il solo errore presente sul fit, ma è
stato necessario tener conto degli errori dovuti alla converisone dalla carica al
numero di fotoelettroni. È stato considerato un errore sistematico del 2.15%
per tutte le sorgenti in cui si è utilizzato il valore del singolo fotoelettrone
di 1.21 pC, invece per il solo Co l’errore è del 2.55% in quanto la carica del
singolo fotoelettrone è di 0.435 pC. Il 2.15% e il 2.55% sono gli errori relativi
percentuali dei valori di singolo fotoelettrone utilizzati. Gli errori sistematici
su descritti sono stati sommati in quadratura con quelli ottenuti dai fit.
Questa grandezza è stata inoltre misurata per tutte le sorgenti utilizzate
per calibrare il rivelatore a scintillatore liquido. Tutti i valori della resa in
luce calcolati, con i relativi errori, sono riportati in tabella 3.7
Source
133
Ba
137
Cs
210
Pb
241
Am
133
Ba
137
Cs
60
Co
γ Energy [keV]
31
32.3
47
60
356
661.64
1173.2
LY [γ/keV ]
2.22 ± 0.03
2.37 ± 0.03
2.44 ± 0.03
2.56 ± 0.03
2.36 ± 0.03
2.78 ± 0.03
2.58 ± 0.03
Tabella 3.7: Resa in luce delle sorgenti utilizzate per la calibrazione del
rivelatore a scintillatore liquido.
Per calcolare la risoluzione dello scintillatore liquido è stata utilizzata la
formula vista nel paragrafo 2.2:
R = 2.35
σ
E
I valori necessari per calcolare questa grandezza, sono ottenuti dai fit degli
spettri in energia delle diverse sorgenti radioattive, riportati in tabella 3.6. I
risultati ottenuti della risoluzione con i relativi errori sono riportati in tabella
3.8.
La risoluzione è stata successivamente graficata in funzione dell’energia
dei raggi γ incidenti ed è stato eseguito un fit utilizzando la funzione R =
p0
√
+ p1
+ p2 dove p0, p1 e p2 sono tre parametri che si ottengono dal fit.
E
E
42
RUN
6163
6162
6161
6160
6163
6162
6165
R[%]
67.37
76.41
41.77
34.28
59.50
22.60
28.40
σR
0.59
2.30
0.43
0.22
1.10
0.58
0.78
Tabella 3.8: Valori della risoluzione in energia ed il suo errore calcolati per
le sorgenti radioattive usate per la calibrazione.
Figura 3.21: Andamento della risoluzione in funzione dell’ energia delle sorgenti radioattive. Per eseguire il fit è stata utilizzata la funzione
R = √p0E + p1
+ p2 dove R è la risoluzione, E l’energia e p0, p1 e p2 i
E
parametri che si ottengono dal fit.
43
Conclusioni
Oggetto di questo lavoro di tesi è stata la calibrazione di un rivelatore a scintillatore liquido. Il rivelatore che è stato calibrato è costituito da uno scintillatore liquido della SCIONIX HOLLAND modello LS EJ-309 accoppiato al
PMT 9821B della ET Enterprises.
In primo luogo è stato calcolato il valore della somma delle resistenze del
partitore di tensione del PMT. Sono stati studiati gli spettri di singolo fotoelettrone relativi a diverse tensioni di alimentazioni del PMT attraverso i quali
è stato possibile ottenere la carica corrispondente al singolo fotoelettrone e
quindi il guadagno del PMT che risulta essere di 106 ÷107 come atteso. Infine
tramite l’utilizzo delle sorgenti radioattive di 210 P b, 241 Am, 133 Ba, 137 Cs e
60
Co è stato verificato l’andamento lineare della resa in luce dello scintillatore in funzione delle energia rilasciata da tali sorgenti ed è stata calcolata la
risoluzione.
44
Bibliografia
[1] LEO, William R. Techniques for nuclear and particle physics experiments:
a how-to approach. Springer Science & Business Media, 2012.
[2] KNOLL, Glenn F. Radiation detection and measurement. John Wiley &
Sons, 2010.
45