equazioni di maxwell e onde elettromagnetiche

EQUAZIONI DI MAXWELL
CAMPO ELETTRICO INDOTTO
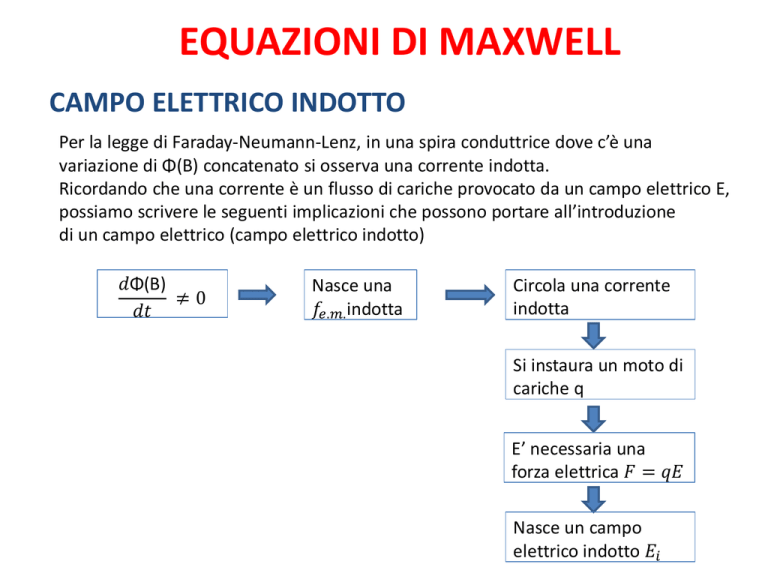
Per la legge di Faraday-Neumann-Lenz, in una spira conduttrice dove c’è una
variazione di Φ(B) concatenato si osserva una corrente indotta.
Ricordando che una corrente è un flusso di cariche provocato da un campo elettrico E,
possiamo scrivere le seguenti implicazioni che possono portare all’introduzione
di un campo elettrico (campo elettrico indotto)
𝑑Φ(B)
≠0
𝑑𝑡
Nasce una
𝑓𝑒.𝑚. indotta
Circola una corrente
indotta
Si instaura un moto di
cariche q
E’ necessaria una
forza elettrica 𝐹 = 𝑞𝐸
Nasce un campo
elettrico indotto 𝐸𝑖
CAMPO ELETTRICO INDOTTO
Possiamo pensare ad un’interpretazione diversa dovuta a Maxwell
(in rosso) per spiegare l’insorgere di una corrente indotta nella spira
Se in una regione dello spazio si ha una variazione del flusso
𝑑Φ(B)
magnetico, 𝑑𝑡 ≠ 0, si crea una nuova proprietà dello spazio
detta campo elettrico indotto
𝑑Φ(B)
≠0
𝑑𝑡
Nasce una
𝑓𝑒.𝑚. indotta
Circola una corrente
indotta
Si instaura un moto di
cariche q
E’ necessaria una
forza elettrica 𝐹 = 𝑞𝐸
Nasce un campo
elettrico indotto 𝐸𝑖
CAMPO ELETTRICO INDOTTO
Questa proprietà dello spazio poi si manifesta su
un’eventuale spira conduttrice (o circuito) presente
nella regione, con una corrente indotta
IN CONCLUSIONE:
UN CAMPO MAGNETICO VARIABILE GENERA
UN CAMPO ELETTRICO INDOTTO
Il campo indotto non dipende dalla presenza o meno
di un circuito; togliendo il circuito non avremo più la
corrente ma continuerà ad essere presente il campo
elettrico
Caratteristiche di questo campo elettrico indotto
Consideriamo che in una regione dello spazio in cui è presente un campo
magnetico variabile nel tempo ci sia un circuito (o semplicemente una linea
chiusa) 𝛾 di superficie S. Per la legge di Faraday Neumann- Lenz si genera una
f.e.m. indotta nel circuito data da :
𝑓𝑒.𝑚.
𝑑Φ(B)
=−
𝑑𝑡
La 𝑓𝑒.𝑚. è il lavoro per unità di carica necessario per spostare una carica q lungo la
curva 𝛾.
𝐿
𝑓𝑒.𝑚. =
𝑞
Suddividiamo la curva in tratti piccolissimi ∆𝑙𝑘 così piccoli in modo da essere
considerati rettilinei e tali che in ciascuno di essi la forza 𝐹𝑘 sulla carica rimanga
costante. Il lavoro elementare ∆𝐿𝑘 per spostare una carica q lungo il tratto ∆𝑙𝑘 è
∆𝐿𝑘 = 𝐹𝑘 ∙ ∆𝑙𝑘 . Il lavoro totale per spostare la carica q lungo l’intera curva è:
𝐿=
∆𝐿𝑘 =
𝑘
𝐹𝑘 ∙ ∆𝑙𝑘 .
𝑘
Quindi la forza elettromotrice si può scrivere:
𝑓𝑒.𝑚. =
Il rapporto
𝐹𝑘
𝑞
𝐿
=
𝑞
𝑘 𝐹𝑘
∙ ∆𝑙𝑘 .
=
𝑞
𝑘
𝐹𝑘
∙ ∆𝑙𝑘 .
𝑞
è il campo elettrico indotto nel tratto ∆𝑙𝑘 della curva, quindi:
𝑓𝑒.𝑚. =
𝐸𝑘 ∙ ∆𝑙𝑘 .
𝑘
Il membro di destra è la circuitazione del campo elettrico indotto lungo la curva 𝛾:
𝐶(𝐸) =
𝐸𝑘 ∙ ∆𝑙𝑘 .
𝑘
La legge di Faraday-Neumann-Lenz si può riscrivere nella forma:
𝑑Φ(B)
𝐶 𝐸 =−
𝑑𝑡
La
𝑘 𝐸𝑘
∙ ∆𝑙𝑘 . si può riscrivere tramite integrale lungo una linea chiusa come:
𝐸 ∙ 𝑑𝑙 = −
𝑑Φ(B)
𝑑𝑡
Dalla nuova formulazione della legge di Faraday-Neumann osserviamo che la
circuitazione del campo elettrico indotto è diversa da zero per cui:
IL CAMPO ELETTRICO INDOTTO NON E’ CONSERVATIVO
Se ci troviamo nel caso stazionario in cui non varia il campo magnetico, ossia se:
𝐵 = 𝑐𝑜𝑠𝑡 =>
𝑑Φ(B)
= 0 =>
𝑑𝑡
𝐸 ∙ 𝑑𝑙 = 0
Abbiamo un campo elettrico conservativo, perché la circuitazione lunga una linea
chiusa è nulla. Non è più un campo elettrico indotto
L’equazione
𝑑Φ(B)
𝐸 ∙ 𝑑𝑙 = −
𝑑𝑡
Include anche il caso stazionario di campo elettrostatico
𝑬 è il campo elettrostatico per i casi stazionari e il campo elettrico indotto per i
casi variabili, non stazionari
Campi elettrici
Campo
elettrostatico
Circuitazione = 0
il campo è conservativo
(creato da cariche)
Campo
elettrico
indotto
Circuitazione  0
il campo
non è conservativo
(creato da variazioni di B)
Equazioni di Maxwell
7
CAMPO MAGNETICO INDOTTO
𝐸 ∙ 𝑑𝑙 = −
𝑑Φ(B)
𝑑𝑡
L’equazione
dice che in una regione in
cui c’è un campo magnetico che varia si genera un campo elettrico
Questa interpretazione della Legge di Faraday fa sorgere una
domanda naturale: è vero anche la situazione simmetrica?
Se in una regione di spazio c’è un campo elettrico che varia, si crea
un campo magnetico?
La risposta è affermativa e questa evidenza sperimentale si
sviluppa in una teoria grazie a Maxwell partendo dall’evidenziare i
limiti della Legge di Ampere
𝐶𝛾 (B)= 𝜇0 𝑖𝑐
Dove 𝑖𝑐 è la corrente
concatenata alla linea 𝛾
Che possiamo riscrivere tramite integrale lungo una linea chiusa
𝐵 ∙ 𝑑𝑙 = 𝜇0 𝑖𝑐
8
Il campo magnetico indotto
Consideriamo un condensatore piano in carica, come mostrato in
figura:
• Intorno al filo conduttore si genera un campo magnetico variabile
nel tempo che permane fino al completamento della carica
• Tra le piastre del condensatore
- si genera un campo elettrico variabile che aumenta fino a
raggiungere il valore massimo quando le piastre sono
completamente cariche
- si genera anche un debole campo magnetico nonostante
l’assenza di corrente
In conclusione si osserva sperimentalmente che c’è una simmetria:
Così come un campo magnetico variabile genera un campo
elettrico indotto, anche un campo elettrico variabile genera
un campo magnetico indotto. Entrambi i campi indotti sono
concatenati ai campi "induttori"
( E ) 
q

( B)  0
 
d ( B)
E

d
l



dt
 
 B  dl   i
Flusso
Dove poter
inserire questa
simmetria?
Circuitazione
10
Asimmetrie campi elettrici e magnetici
q

( E ) 

( B)  0
 
d ( B)
 E  dl   dt
 
B

d
l


i


Esistono cariche isolate, ma
non poli magnetici isolati
Se un campo magnetico
variabile crea un campo
elettrico indotto, è vero il
viceversa?
SI, APPENA VISTO, MA
COME MODIFICHIAMO
L’EQUAZIONE? 11
GENERALIZZAZIONE DELLA LEGGE DI AMPERE
Tentiamo di ristabilire la simmetria
• C’è un errore dimensionale
q
tra i due membri
( E ) 
• Il segno – va cambiato con

quello + poiché la
( B)  0
circuitazione del campo
magnetico calcolata lungo
d ( B)
una linea chiusa avvolta
E  dl  
intorno alle linee di E è
dt
positiva in corrispondenza
d

(
E
)
di un aumento del flusso
B

dl


i
B  dl  
??? del campo E


dt
12
Carica di un condensatore
Abbiamo visto che:
• La corrente di carica crea un campo magnetico
• Dentro il condensatore si crea un campo elettrico variabile; anche il
campo elettrico variabile nel vuoto genera un campo magnetico
(debole)
E
B
B
Qui c’è corrente
Qui c’è corrente
Qui NO
Ma….LA NATURA NON FA SALTI ed inoltre
la variazione di flusso del campo elettrico nel condensatore si
comporta come una corrente nel filo in quanto genera un campo
13
magnetico
Esperimento di Maxwell
• Applicando la legge di Ampere,
Maxwell osserva che la circuitazione
del campo magnetico lungo S1 prima e
dopo il condensatore è costante e non
nulla, mentre è nulla lungo S2 se non si
tiene conto dell’esistenza di una
‘corrente’ anche tra le armature
• Ricordando il fondamentale principio
della fisica, la natura non fa salti,
ipotizza l’esistenza, all’interno del
condensatore, di una nuova corrente
corrente di spostamento, di valore
pari a quella di carica del
condensatore.
Alla ricerca del termine mancante
• L’unica cosa presente nel condensatore è il campo
elettrico.
• Pertanto Maxwell trova la relazione tra questo e la
corrente di carica i.
• La variazione di carica sul condensatore vale: Q  it

E

• Il campo E vale:
Q


dove la densità di carica vale:
S
dove S è la superficie delle armature del condensatore.
• Quindi la variazione del flusso del campo elettrico nel
condensatore è pari a:

Δσ
ΔQ
ΔQ
ΔΦ E  Δ(ES) 
S
S
ε
Sε
ε
Il calcolo della corrente di spostamento
Q  it
Ricordando che:
segue:

 E 
Q


it

Esplicitando la corrente abbiamo che:
Maxwell la chiama corrente di
spostamento, che indicheremo col
simbolo is.

 E
is  
t

 E
i 
t
Il teorema di Ampère-Maxwell
Maxwell modifica il teorema di Ampère come segue:

C B   i  is 
Sostituendo is otteniamo:

 

 E
C B   i  

t



Che prende il nome di teorema di Ampère-Maxwell.

OSS:  E
d ( B)
dt
t
È la variazione del flusso di E nel tempo ∆𝑡, mentre con il simbolo
Si indica la derivata del flusso rispetto al tempo, ossia quanto l’intervallo di
tempo in cui si misura la variazione temporale è prossimo a zero
Equazioni di Maxwell definitive
( E ) 
q

( B)  0

 
d ( B)
E

d
l



dt

 

d ( E ) 


B

d
l



i





dt


Un campo E variabile
crea un campo B
Un campo B variabile
crea un campo E
… e così via
OSS: Rappresentiamo le equazioni utilizzando derivate temporali (variazioni piccole di
tempo)
18
L’importanza di Maxwell
• Con l’aggiunta del suo termine mancante, Maxwell modifica
profondamente le equazioni dei campi elettrici e magnetici,
mostrando l’interdipendenza tra i due.
• Per questo da Maxwell in poi si potrà parlare di campi
elettromagnetici.
• Questo è il motivo per cui le precedenti equazioni, scoperte
dai predecessori di Maxwell, dove Maxwell aggiunge solo un
piccolo termine, giustamente prendono il nome di equazioni
di Maxwell.
OSS: Per completare la descrizione delle interazioni elettromagnetiche,
in particolare per descrivere l’azione dei campi elettrici e magnetici su
una particella carica in moto, ricordiamo che bisogna aggiungere una
quinta equazione, l’ EQUAZIONE DI LORENTZ
𝐹 = 𝑞(𝐸 + 𝑣 × 𝐵)
EQUAZIONI DI MAXWELL NEL CASO STATICO
Le equazioni di Maxwell nel caso di campi elettrici e
magnetici costanti diventano:
( E ) 
q

( B)  0
 E  dl  0
B

dl



i

Nel caso statico
NON CI SONO RELAZIONI TRA
CAMPO ELETTRICO E MAGNETICO
EQUAZIONI DI MAXWELL IN ASSENZA DI
CARICHE E DI CORRENTI
La simmetria di cui si è parlato è ancora più evidente
riscrivendole nel caso in cui non siano presenti né
cariche e né circuiti percorsi da correnti.
In tal caso non ci sono sorgenti, cioè Q = 0 ed i = 0
Pertanto le equazioni si riscrivono nel seguente modo:
 E   0
 B   0
d ( B )
C E   
dt
d ( E )
C B   
dt
Da questa situazione si
arriverà a scoprire le
onde elettromagnetiche
CAMPO ELETTROMAGNETICO
Maxwell sistemò in una teoria unitaria tutte le leggi
dei fenomeni elettrici e magnetici.
In questa teoria i due tipi di campi sono due aspetti
di una stessa entità: il campo elettromagnetico.
CAMPO ELETTROMAGNETICO
Dalla terza e quarta equazione di Maxwell in assenza di cariche e di
correnti segue che:
Un campo magnetico variabile genera un campo elettrico indotto
che, se risulta a sua volta variabile, produce un secondo campo
magnetico che, nel caso anche questo fosse variabile, si
produrrebbe un secondo campo elettrico indotto e così via,
generando una perturbazione elettromagnetica, ossia una
perturbazione del campo elettromagnetico
Affinché di possa creare una perturbazione elettromagnetica,
i campi elettrici e magnetici devono essere VARIABILI
Ciò è possibile accelerando una carica elettrica
-
Una carica elettrica accelerata genera un campo
elettrico variabile; ma una carica in moto equivale
a una corrente, e si genera quindi anche un
campo magnetico variabile (poiché il moto della
carica è accelerato e la sua velocità è variabile).
Si genera così un’onda elettromagnetica
La perturbazione elettromagnetica si propaga nello
spazio da un punto a uno immediatamente vicino a una
velocità costante ed è in grado di autosostenersi
La velocità con cui si propaga la perturbazione del
campo elettromagnetico è la velocità della luce.
La luce stessa è un’onda elettromagnetica di particolare
frequenza
ONDA ELETTROMAGNETICA
Un’onda elettromagnetica è prodotta da oscillazioni di
cariche elettriche ed è l’effetto di una vibrazione di un
campo elettrico e di un campo magnetico che si
propagano nello spazio con la stessa velocità.
La velocità, c, che coincide con quella della luce, vale:
𝑚
8
𝑐 = 2,99 79 ∙ 10
𝑠
Dalla terza e quarta equazione di Maxwell in assenza di
cariche e correnti, con un semplice calcolo si arriva al
seguente risultato
𝑐=
1
𝜀0 𝜇0
=
8𝑚
2,99 79 ∙ 10
𝑠
La propagazione delle onde elettromagnetiche
L’apparato più semplice per produrre un’onda
elettromagnetica, quindi un campo elettromagnetico
variabile nel tempo, è l’antenna a dipolo elettrico
– si può schematizzare con un dipolo elettrico
oscillante
• la radiazione emessa prende il nome di radiazione da
dipolo elettrico
– il campo elettrico e il campo magnetico indotto sono
perpendicolari tra loro e legati da una relazione di
proporzionalità diretta
– c è la velocità della luce
ANTENNA A DIPOLO ELETTRICO
Heinrich Rudolf Hertz nel 1887 costruì la prima antenna
trasmittente e ricevente e confermò sperimentalmente l’esistenza
delle onde elettromagnetiche previste teoricamente da Maxwell
Il movimento delle
cariche all’interno
dell’antenna
alimentata da un
generatore di
corrente alternata
può essere
schematizzato
attraverso un dipolo
elettrico oscillante.
ONDE ELETTROMAGNETICHE
La rappresentazione temporale dell’onda elettromagnetica
generata dall’antenna a dipolo elettrico in un certo punto P, a
quattro differenti istanti (fissata la posizione dell’osservatore).
I due campi sono fra loro perpendicolari.
(A) All’istante iniziale il campo elettrico è massimo ed è diretto verso l’alto
(B) Ad un istante successivo il campo elettrico diminuisce e si genera un campo
magnetico indotto perpendicolare al piano che contiene il campo elettrico.
(C) Nei casi (B) (C) (D), i campi si propagano verso destra alla velocità della luce e i
loro moduli sono legati istante per istante dalla relazione:
Le funzioni che rappresentano i campi sono sinusoidali e si propagano su due piani
perpendicolari fra loro
ONDE ELETTROMAGNETICHE
La rappresentazione spaziale dell’onda elettromagnetica a
un determinato istante t. L’onda si propaga lungo l’asse x
con una lunghezza d’onda ʎ.
Le proprietà delle onde elettromagnetiche
Le onde elettromagnetiche
– sono onde trasversali
– godono delle stesse proprietà delle onde
periodiche in generale
– possono propagarsi sia in un mezzo sia nel vuoto
– danno origine agli stessi fenomeni della luce
• riflessione, rifrazione, interferenza, diffrazione