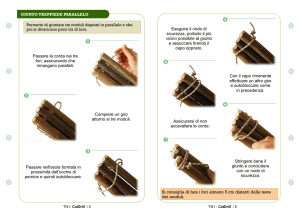
Programma del corso di
ALGEBRA IV
tenuto dalla Prof. Mercede MAJ
nell'anno accademico 2006/2007
1 - Numeri cardinali
Richiami su: insiemi equipotenti, potenza di un insieme, numero cardinale (o
cardinalita’ di un insieme), insiemi numerabili, insiemi finiti e infiniti, cardinali finiti
e infiniti.
Relazione d’ordine nella classe dei numeri cardinali. Teoremi di Hartogs e di
Cantor-Schröder-Bernstein. Teorema di tricotomia.
Aritmetica dei numeri cardinali. Somma di numeri cardinali. Proprieta’. Prodotto
di numeri cardinali. Proprieta’. Somma e prodotto di due cardinali non entrambi
finiti. Numero cardinale dell’unione di insiemi di uguale cardinalità.
2 – Moduli
Definizione di modulo sinistro (destro) su un anello unitario, esempi. Regole di
calcolo in un modulo. Omotetie. Legami tra il modulo M su R e gli anelli R e End
M.Moduli sull’anello degli interi Z. Legame tra moduli sinistri e moduli destri.
Sottomoduli. Sottomodulo generato da una parte, sottomodulo generato da una
famiglia di sottomoduli. Moduli ciclici, moduli finitamente generati. Somma diretta
di sottomoduli. Sommandi diretti. Esempi,
Modulo quoziente. Omomorfismi tra moduli. Teoremi di omomorfismo. Il gruppo
Hom R(M, N) degli R-omomorfismi di un modulo M in un modulo N. L’anello EndRM
degli R-omomorfismi di un modulo M. Sequenze di moduli, sequenze corte, sequenze
esatte. Esempi. Teoremi sulle sequenze sulle sequenze. Lemma dei 5, anche in forma
debole. Sequenze corte spezzate, loro caratterizzazioni. Push-out , pull-back (dim
facoltativa)
Moduli semplici. Lemma di Schur. Moduli indecomponibili . Moduli fedeli.
Moduli di torsione e senza torsione. Esempi.
Prodotto diretto esterno di una famiglia di moduli. Esempi. Proprietà universale
del prodotto diretto. Somma diretta esterna di una famiglia di moduli. Esempi.
Proprietà universale della somma diretta.
Parti libere, parti dipendenti di un modulo. Basi di un modulo. Moduli liberi., loro
caratterizzazioni. Esempi. Proprietà universale dei moduli liberi. Teorema di Von
Dyck. Esempio di modulo libero con basi non equipotenti. Equipotenza di basi
infinite. Anelli con la proprietà della dimensione invariante. Esempi.
Moduli proiettivi , loro caratterizzazioni. Esempi. Legami tra moduli liberi e
moduli proiettivi. Somma diretta di una famiglia di moduli proiettivi.
Moduli iniettivi. Esempi. Prodotto diretto di una famiglia di moduli iniettivi.
Criterio di Baer. Moduli divisibili. Legami tra moduli divisibili e moduli iniettivi.
Immersione di un modulo in un modulo iniettivo.
Inviluppo iniettivo (dim facoltativa) .
Moduli Noetheriani e Artiniani. Esempi, proprieta’, caratterizzazioni.
Lemma di Fitting (dim facoltativa). Teorema di Krull, Remak, Schmidt, Wedderburn
(dim facoltativa). Moduli dotati di serie di composizione (dim facoltativa). Teorema
di Jordan-Holder (dim facoltativa)
Moduli semisemplici (dimostrazioni facoltative)
Moduli su di un anello principale (dimostrazioni facoltative)
Prodotto tensoriale di moduli. Esistenza e unicità a meno di isomorfismi. Regole
di calcolo. Esempi. Prodotto tensoriale di omomorfismi (dimostrazioni facoltative).
Prodotto tensoriale di moduli su di un anello commutativo
Testi consigliati
M. Curzio, P. Longobardi, M. Maj - Lezioni di Algebra - Liguori , 1994.
T.W. Hungerfort - Algebra - Springer-Verlag, Berlin 1973.
e inoltre
T.S. Blyth - Module Theory - Clarendon Press , Oxford, 1990.
B. Hartley –T. Hawkes –Rings, modules and linear Algebra, Chapman & Hall,
London 1970.
F. Kasch – Modules and rings, Academic Press, London-New York, 1982.
J: Lambek – Lectures on rings and modules, Chelsea, N.Y. 1986.
S. Lang - Algebra, Addison-Wesley, Reading, Mass., 1965.