Secondo Principo della Dinamica

Palermo 29 Novembre 2004
I tre principi della dinamica
Lo studio della Dinamica iniziò tre secoli fa da Galileo Galilei e da Newton.
Lo scopo della Dinamica consiste nel determinare come si muove un oggetto quando si conoscono
le forze a cui è sottoposto. Si può così prevedere, oltre alla sua traiettoria, anche la posizione e la
velocità che ha in ogni istante.
La Dinamica si fonda su tre principi:
1) Il primo principio o principio d’inerzia
2) Il secondo principio o legge fondamentale della Dinamica
3) Il terzo principio o principio di azione e reazione
Il secondo principio della dinamica, enuncia che:
L’accelerazione di un punto materiale è in ogni istante direttamente proporzionale alla forza
applicata; forza e accelerazione hanno lo stesso verso.
F = ma
F corrisponde alla forza applicata, m corrisponde alla massa dell’oggetto e a all’accelerazione che
esso acquista quando è applicata la forza.
L’unità di misura della forza nel Sistema Internazionale è il newton (N), che corrisponde alla forza
necessaria a fare accelerare di 1 m/s2 un corpo di massa 1 kg .
1
Il secondo principio della dinamica
Verifichiamo il secondo principio della dinamica, risolvendo un problema così configurato:
A
B
Un carrello di massa 0,4 kg, posto su una rotaia a cuscino d’aria, viene accelerato da un peso
di
0,3 kg che cade. Il filo è inestensibile e di massa trascurabile. La carrucola è ben lubrificata e
l’attrito trascurabile.
Calcoliamo la tensione del filo che trascina il carrello, e cosa accadrebbe se appendessimo un
secondo pesetto al primo. La tensione raddoppierà?
Sul peso B, che cade, agisce la forza di gravità, che vale:
P = mg = (0,3 kg) * (9,8 m/s2) = 2,94 N
Utilizzando il principio della dinamica, e le relative formule inverse, sappiamo che l’accelerazione
che acquista un corpo è pari al rapporto tra la Forza che è impressa e la massa del corpo, nel nostro
caso la Forza non è altro che la forza di gravità agente sul peso B, mentre la massa è la somma del
carrello A e del peso B:
a=
F
2,94 N
=
= 4,2 m/s2
mtot
(0,3kg  0,4kg)
Il peso del carrello A è equilibrato dalla reazione vincolare del piano, dovuto al cuscino d’aria;
quindi la forza risultante agente sul carrello è la tensione T del filo.
E quindi: T = (0,4 kg) * (4,2 m/s2)= 1,68 N.
Ora conosciamo la tensione che trascina il filo, vediamo cosa accadrebbe se attaccassimo un altro
peso d’uguale massa; moltiplichiamo per due la forza di gravità che agiva su un peso per avere
quella che agirà su due:
P2 = 2 * (2,94 N) = 5,88 N.
Quindi l’accelerazione sarà di:
a=
F
5,88 N
=
= 5,88 m/s2
mtot
(0,6kg  0,4kg)
Segue che la nuova tensione del filo sarà di :
T2 = (0,4 kg) * (5,88 m/s2) = 2,35 N.
Quindi la prima tensione era di 1,68 N mentre la seconda di 2,35 N, si nota dunque, la seconda non
è il doppio della prima.
2
Successivamente, per verificare il secondo principio della dinamica, abbiamo ricreato il problema
appena risolto utilizzando un software.
Nello specifico abbiamo utilizzato: Interactive Physics,
questo, è un laboratorio multimediale lavorante su 2
dimensioni, che permette la simulazione virtuale di una
gran quantità d’esperimenti fisici, alcuni dei quali,
impossibili da realizzare nella realtà poiché sarebbe
impossibile creare le situazioni adatte, come per esempio
la possibilità di eliminare la forza d’attrito.
L’ambiente di lavoro è il seguente:
Barra degli
strumenti
Righello
Strumenti
di lavoro
Piano di lavoro
Abbiamo simulato l’ambiente nel quale si svolgeva il problema, precedentemente analizzato, nel
software, utilizzato lo strumento per creare gli oggetti, quali peso, carrello, piano; tolta la forza
d’attrito settando le proprietà degli oggetti, inserito la carrucola ed infine unito gli oggetti con un
filo.
3
Una volta sistemati i nostri oggetti e assegnatagli la massa,elimineremo la forza d’attrito utilizzando
il pannello Proprietà per poi avviare l’animazione.
Provata l’animazione possiamo anche inserire dei
grafici, creati automaticamente dal software, e
inoltre farci mostrare il vettore accelerazione d’ogni
oggetto.
Infatti, cliccando sull’oggetto del quale si vuole
misurare: posizione, velocità o accelerazione.
Apriremo
il
menù
Misura,
selezioneremo
Posizione, Velocità o Accelerazione, secondo le
esigenze, e selezionando l’asse nel quale si trova la voce prescelta, sarà creato un grafico.
Per quanto riguarda la visualizzazione del vettore direttamente sull’oggetto, aprendo questa volta il
menù Definisci cliccheremo su Vettori per selezionare la voce che c’interessa, sarà così visualizzato
il vettore, aggiornato in tempo reale sull’oggetto. Impostati
tutti questi parametri i
risultati ottenuti sono
quelli da noi attesi, sia per
l’accelerazione di 4,2 m/s2,
sia per la tensione T del
filo che è di 1,6 N:
Con IP possiamo inoltre misurare con esattezza il tempo,
modificare sia il tipo d’accelerazione che può essere di gravità o planetaria, che possono essere più
o meno forti; è possibile inserire
l’attrito
dell’aria;
forze,
ruote
dentate, molle e molto altro ancora.
Abbiamo inoltre utilizzato IP per
verificare il principio della
dinamica applicato ad un corpo in
caduta libera, infatti, il peso P di un
corpo, è il prodotto
dell’accelerazione gravitazionale
per la sua massa, cioè: F = ma
diventa P = gm.
4
Abbiamo, inoltre, visto un film, dal titolo: “Inerzia e Moto”, riguardante sempre i principi della
dinamica.
Il film è basato su di uno scienziato che, tramite degli esperimenti in laboratorio,
dimostra il principio della dinamica.
Nel film si dimostra che serve una forza per fare variare lo stato del moto di un
oggetto; nel fare ciò entra in lavoro il fisico, il quale deve creare un sistema più
semplice da laboratorio, in modo da “diffalcare” gli impedimenti, come disse Galileo Galilei.
Nel mondo non semplificato, se si spinge un corpo su di un tavolo, il corpo scivola, si muove e poi
si ferma; ma ciò e dovuto agli attriti, quindi noi cercheremo di semplificare cercando di levare gli
attriti.
Quindi ora entriamo nel Laboratorio, e semplifichiamo. Innanzitutto il nostro oggetto sarà un
recipiente di metallo contente ghiaccio secco (CO2), con sotto
un disco da cui fuoriesce un gas, formando così un cuscinetto
d’aria. Ciò diminuisce di molto
l’attrito tra l’oggetto e la lastra di
vetro ben lucidata che copre il tavolo
dove poggia il nostro recipiente.
Notiamo che se si spinge il disco, esso si muoverà in linea retta, per
verificare ciò utilizziamo una scala graduata su di un’asta, e osserviamo il disco dall’alto.
Il disco non tende a fermarsi fin quando non lo fermiamo noi.
Scattando delle foto ogni secondo notiamo che il disco percorre spazi uguali in tempi uguali, nel
nostro caso 16 cm/s; quindi un corpo che si muove non disturbato da
altre forze, mantiene il suo moto e la sua velocità costante e
percorrendo lo spazio in modo retto.
Ora dimostriamo che un oggetto dove ci sono forze equilibrate si
muove a velocità costante.
Dovremmo quindi applicare una forza non equilibrata all’oggetto, e per comodità ne applichiamo
una costante. Il peso dell’oggetto è equilibrato dal cuscinetto di gas, quindi la forza peso è
equilibrata, ma noi applicheremo una forza costante all’oggetto,
parallela al piano. Per essere certi che la forza sia costante
utilizzeremo un elastico attaccato ad un filo che tireremo. Se
applicheremo una forza sempre costante l’elastico, si deformerà
sempre nello stesso modo.
Ora scattando fotografie sempre ad intervalli di un secondo
5
notiamo che le di stanze percorse dell’oggetto sono diverse in ogni intervallo, infatti, ogni secondo
che passava il disco percorreva più spazio. Creando il grafico spazio/tempo, otteniamo una retta che
ci conferma un moto uniformemente accelerato.
Vogliamo inoltre vedere cosa succede se applichiamo 2
forze di stessa intensità alla prima. Per fare ciò attaccheremo
2 elastici, in modo tale che quando applicheremo un forza
tale da fare piegare entrambi gli elastici nello stesso modo di
quando ne avevamo attaccato solamente uno, saremo sicuri
di avere raddoppiato la forza e di mantenerla costante.
Una volta finito il cambiamento di velocità sarà doppio rispetto a quello di prima. Quindi
raddoppiando la forza applicata si raddoppia anche l’accelerazione.
Possiamo concludere, dicendo che:
 Quando su di un oggetto si applica una forza non equilibrata, l’accelerazione dell’oggetto
è direttamente proporzionale alla forza applicata.
 E’ necessaria una forza per cambiare il moto di un corpo.
 La rapidità di variazione della velocità e proporzionale alla forza applicata.
Alla fine del film, ci viene svelato chi era ad applicare le forze in modo costante. A fare ciò infatti
non poteva certo essere un essere umano, ma era un disco identico al primo, con la sola differenza
di essere su di un tavolo inclinato, e quindi, questo quando scendeva per il tavolo si trascinava
anche l’altro.
6
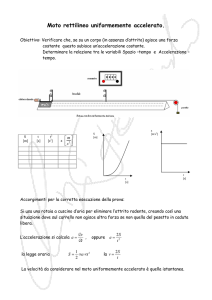
Abbiamo deciso di provare noi stessi un esperimento in laboratorio per dimostrare il principio della
dinamica.
Per fare ciò utilizzeremo un carrello di peso 535,1 g, pesato con una bilancia elettronica; un binario
dove fare muovere il carrello, un filo, una carrucola, un peso di 50g, e un sonar che è collegato ad
un PC, con il quale potremo automaticamente ricevere i dati e creare grafici.
535,1 g
50g
Sappiamo che F = ma, nel nostro caso F è la forza peso del peso di 50 g, mentre la massa è quella
complessiva del carrello più il peso.
F = ma  P =(M+m)a  mg = (M+m)a  a =
50
* 9,8 = 0,84 m/s2
50  531
Il secondo principio della dinamica è stato così da noi verificato.
Gabriele Pergola II A
7