UNITÀ 2. DISEQUAZIONI ALGEBRICHE 1. Generalità e definizioni

UNITÀ 2.
DISEQUAZIONI ALGEBRICHE
1. Generalità e definizioni sulle disequazioni algebriche.
2. Disequazioni di primo grado.
3. Disequazioni di secondo grado.
4. Disequazioni di grado superiore al secondo.
5. Disequazioni fratte.
6. Sistemi con disequazioni di primo grado.
7. Sistemi con disequazioni di secondo grado.
8. Sistemi con disequazioni di grado superiore al secondo.
9. Sistemi con disequazioni fratte.
10. Equazioni irrazionali.
11. Disequazioni irrazionali di prima specie e di seconda specie.
12. Il valore assoluto e le sue proprietà.
13. Equazioni con valore assoluto.
14. Equazioni con più valori assoluti.
15. Disequazioni con valore assoluto.
16. Disequazioni con più valori assoluti.
17. Problemi vari che si risolvono con disequazioni o con sistemi di disequazioni.
1. Generalità e definizioni sulle disequazioni algebriche.
Una disequazione algebrica è una disuguaglianza tra due espressioni contenenti un’incognita, che è verificata
soltanto per alcuni valori dell’incognita.
Per esempio, la disequazione 5x  4  x  2
contenente l’incognita x, non è verificata per x  0 ma è verificata per x  2 .
Le soluzioni di una disequazione sono tutti i valori dell’incognita che, sostituiti nella disequazione, verificano la
disuguaglianza.
Risolvere una disequazione significa trovare tutte le sue soluzioni.
Una disequazione si dice impossibile se non ha alcuna soluzione. Per esempio x2 1 0 è impossibile.
Le disequazioni algebriche sono quelle che al primo e al secondo membro contengono polinomi, o frazioni
algebriche o espressioni irrazionali, come nei seguenti esempi:
5x2  4x  x  2 disequazione algebrica razionale intera;
x 1
 1 x
x2
disequazione algebrica razionale fratta;
3x  1  x  4
disequazione algebrica irrazionale intera;
x2
 1  4x
x 1
disequazione algebrica irrazionale fratta.
Una qualunque disequazione, dopo aver svolto gli opportuni calcoli, si riconduce sempre ad una delle seguenti
forme:
ax  b  0
se è di primo grado;
ax2 bxc  0
ax3  bx2  cx d  0
se è di secondo grado;
se è di terzo grado … e così via.
Due disequazioni si dicono equivalenti se hanno le stesse soluzioni.
Per risolvere una disequazione bisogna trasformarla in una disequazione equivalente applicando ripetutamente
il principio di addizione e il principio di moltiplicazione.
Principio di addizione:
aggiungendo o sottraendo ai due membri di una disequazione uno stesso numero, si ottiene una disequazione
equivalente con lo stesso verso;
da questo principio consegue che è possibile trasportare un addendo dal primo al secondo membro, cambiandolo
di segno.
Principio di moltiplicazione:
moltiplicando o dividendo i due membri di una disequazione per uno stesso numero maggiore di zero, si ottiene
una disequazione equivalente con lo stesso verso.
moltiplicando o dividendo i due membri di una disequazione per uno stesso numero minore di zero si ottiene
una disequazione equivalente con il verso contrario.
Da questo principio consegue che è possibile trasportare un fattore positivo dal numeratore del primo membro al
denominatore del secondo membro o dal denominatore del primo membro al numeratore del secondo membro,
lasciando lo stesso verso della disequazione.
Consegue anche che è possibile trasportare un fattore negativo dal numeratore del primo membro al denominatore
del secondo membro o dal denominatore del primo membro al numeratore del secondo membro, cambiando il
verso della disequazione.
2. Disequazioni di primo grado.
3. Disequazioni di secondo grado.
4. Disequazioni di grado superiore al secondo.
5. Disequazioni fratte.
6. Sistemi con disequazioni di primo grado.
7. Sistemi con disequazioni di secondo grado.
8. Sistemi con disequazioni di grado superiore al secondo.
9. Sistemi con disequazioni fratte.
10. Equazioni irrazionali.
11. Disequazioni irrazionali di prima specie e di seconda specie.
12. Il valore assoluto e le sue proprietà.
Il valore assoluto di un numero a si indica con a ed è uguale allo stesso valore a se a  0 , all’opposto di a se
a0.
 a se a  0
Quindi per definizione di valore assoluto risulta:
a 
 a s e a  0
0 0
5 5
Per esempio: 5  5
Rappresentando i numeri reali su una retta orientata R, il valore assoluto di un numero corrisponde alla distanza
di quel numero dall’origine O.
R
Il valore assoluto possiede importanti proprietà che sono molto utili nella risoluzione di alcune equazioni e
disequazioni che contengono il valore assoluto.
Se x ed y sono due numeri reali qualsiasi, valgono le seguenti proprietà, che si possono dimostrare applicando
la definizione di valore assoluto. Per comprendere e ricordare queste proprietà bisogna pensare al valore
assoluto come una distanza.
1)
x 0
2)
x 0 x 0
3)
x  2 è impossibile
4)
x  2  x  2  x  2
5)
x  x
6)
x  y  x  y  x  y
7)
x  y  x y
8)
x
x

y
y
9)
x  2 2  x  2
10) x  2  x  2  x  2
11) x  y  x2  y2
12) x  x2
13. Equazioni col valore assoluto.
Sono equazioni che contengono l’incognita all’interno di un valore assoluto. L’espressione che si trova nel
valore assoluto si chiama argomento del valore assoluto.
In generale, per risolvere un’equazione con valore assoluto, se è possibile, si cerca di utilizzare qualche
proprietà del valore assoluto per ottenere la soluzione più rapidamente.
Esempio 1. 1  2 x  0  1  2 x  0  2 x  1  x 
Esempio 2.
3x  5  4 equazioneimpos s ibil
e
Esempio 3.
5x  1  2 ;
1
2
5x 1  2  5x 1  2
5x  3  5x  1
x
Esempio 4.
3
1
 x
5
5
x  3  1 2x ;
x  3  1  2x  x  3  1  2x
3x  2   x  4
x
Esempio 5.
3
 x4
2
x  2  x 3  2 ;
( x  2)  ( x  3)  2
x2  3x  2x  6  2
x2 5x  6  2
x2 5x  6  2

x2 5x  6  2
x2 5x  4  0

x2 5x 8  0
  25  16  9
  25  32  7  0
La prima equazione ha
le seguenti soluzioni:
La seconda equazione
non ha soluzioni
x
53
1 e 4
2
L’equazione col valore assoluto ammette perciò due soluzioni: x  1 e x  4
Quando non si può utilizzare alcuna proprietà del valore assoluto bisogna applicare la definizione di valore
assoluto e considerare entrambi i casi: argomento  0 e argomento  0 . Si ottengono così due sistemi da
risolvere: le soluzioni dell’equazione col valore assoluto sono date dall’unione tra le soluzioni del primo sistema
e le soluzioni del secondo sistema.
Esempio 6.
2x  9  x  9
s e 2x  9  0

2x  9  x  9

 s e 2x  9  0

 2x  9  x  9
 2x  9

2x  x  0

 2x  9

 3x  18
9

 x
2


x  0 s oluz.accett.
9

 x
2


x  6 s oluz.accett.

L’equazione col valore assoluto ammette perciò due soluzioni: x  0 e x  6
Esempio 7.
2x  x  1  5
x 1  2x  5
s e x  1  0

x  1  2x  5

 s e x 1  0

 x  1  2x  5
 x 1

x  4 accett.

 x 1

3x  6  x  3 non accett.
L’equazione col valore assoluto ammette perciò solo la soluzione: x  4
14. Equazioni con più valori assoluti.
Se l’equazione contiene più valori assoluti, si studia il segno di ciascuno di essi, si rappresentano i segni su una
retta orientata e per ogni intervallo ottenuto si risolve un sistema.
2x  3  x  2  4
Esempio 1. Risolvere l’equazione:
1° valore assoluto: 2 x  3  0 per 2 x  3 cioè x 
3
2
2° valore assoluto: x 2  0 per x  2
3
2
2


x
1
2
3

s e x 
2


 2x  3  x  2  4
3

x
2


 3x  1
3

x


2

x  1 accett.

3


3

 se  x  2
2


2x  3  x  2  4

 3
 x2
 2

x  5

 3
 x2
 2

x  5 non accett.
 s ex  2
 
2x  3  x  2  4

 x2

3x  9

 x2

x  3 accett.
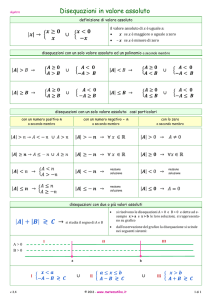
15. Disequazioni con valore assoluto.
Sono disequazioni che contengono l’incognita all’interno di un valore assoluto.
Per risolvere queste disequazioni, se è possibile, si cerca di utilizzare qualche proprietà del valore assoluto per
ottenere la soluzione più rapidamente; se ciò non è possibile bisogna utilizzare la definizione di valore assoluto e
considerare entrambi i casi: argomento  0 e argomento  0 . Si ottengono così due sistemi da risolvere: le
soluzioni della disequazione col valore assoluto sono date dall’unione tra le soluzioni del primo sistema e le
soluzioni del secondo sistema.
Esempio 1. Risolvere la disequazione: 3x  7  2
Si può utilizzare una proprietà del valore assoluto e si ottiene la disequazione:  2  3x  7  2
Si aggiunge  7 a tutti i membri della disequazione:  7  2  3x  2  7  9  3x  5
Si dividono tutti i membri per 3 e si ottiene la soluzione:
3 x  
5
3
Esempio 2. Risolvere la disequazione: 2  5  3
Si può utilizzare una proprietà del valore assoluto e si ottengono due disequazioni:
2  5x  3

2  5x  3
 5x  5

 5x  1
5x  5

5x  1
x 1

x
Esempio 3. Risolvere la disequazione:
1
5
5  2x  4  x
Non si può utilizzare alcuna proprietà del valore assoluto e perciò si devono risolvere due sistemi:
s e 5  2x  0

5  2x  4  x

 s e 5  2x  0

 5  2x  4  x
 2x  5

3x  1

 2x  5

x  9

5

x 
2


x  9
5

x


2

x  1

3

x
1
3

x9
16. Disequazioni con più valori assoluti.
Se la disequazione contiene più valori assoluti, si studia il segno di ciascuno di essi, si rappresentano i segni su
una retta orientata e per ogni intervallo ottenuto si risolve un sistema.
2x  3  x  2  4
Esempio 1. Risolvere l’equazione:
1° valore assoluto: 2 x  3  0 per 2 x  3 cioè x 
3
2
2° valore assoluto: x 2  0 per x  2
3
2
2


x
1
2
3

s e x 
2


 2 x  3  x  2  4

3

x
2


 3x  1
3

x


2

x  1

3

Soluzione finale:
3

 se  x  2
2


2 x  3  x  2  4
x
1
3
x
1
3
 s ex  2
 
2 x  3  x  2  4

 3
 x2
 2

x  5

 x2

3x  9

 3
 x2
 2

 x5

 x2

 x3




x3
x3
17. Problemi vari che si risolvono con disequazioni o con sistemi di disequazioni.