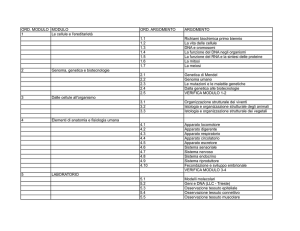
Facoltà di Architettura – Università degli Studi di Genova
Corso di TECNICA DELLE COSTRUZIONI
Chiara CALDERINI
A.A. 2007-2008
LEZIONE 1
IL PROGETTO STRUTTURALE
Parte I. Il concetto di sicurezza
IL PROGRAMMA DEL CORSO
LEZIONE 1 - Il PROGETTO STRUTTURALE
LEZIONE 2 - I MATERIALI E I CARICHI DELLA COSTRUZIONE
STRUTTURA
LEZIONI
LEZIONE 3-5 – PROGETTO DI COSTRUZIONI IN ACCIAIO
LEZIONE 6-7 – PROGETTO DI COSTRUZIONI IN LEGNO
LEZIONE 8-10 – PROGETTO DI COSTRUZIONI IN CLS ARMATO
1 e 1/2 ORA:
TEORIA
+
1 e 1/4 ORA:
LEZIONE 11 – PROGETTO DI COSTRUZIONI IN MURATURA
LEZIONE 12 – ANALISI DI COSTRUZIONI IN MURATURA
LEZIONE 13 – INTERVENTI DI CONSOLIDAMENTO
APPLICAZIONE
IL PROGRAMMA DEL CORSO
RICHIESTA DI CONOSCENZE MINIME
METODO E CRITERI GENERALI
MODALITA’ DI ESAME
LA SICUREZZA STRUTTURALE
IL CONCETTO DI SICUREZZA STRUTTURALE - 1
Codice di Hammurabi (2200 a.C.)
“Se un edificio crolla causando la morte del proprietario, il costruttore
deve essere ucciso; se il crollo dell’edificio causa la morte del figlio del
proprietario, anche il figlio del costruttore deve essere ucciso; se il crollo
dell’edificio produce la morte ad un schiavo del proprietario, il
costruttore è tenuto a fornirgliene un altro; se l’edificio subisce danni
questi devono essere riparati a spese del costruttore”.
LA SICUREZZA STRUTTURALE
IL CONCETTO DI SICUREZZA STRUTTURALE - 2
L’Arte del Costruire
Fino al XIX, la sicurezza delle costruzioni è affidata principalmente al
rispetto delle REGOLE DELLA TRADIZIONE.
Tali regole sono state elaborate nel corso dei secoli, sulla base
dell’esperienza, dell’osservazione di crolli e danni, dell’intuizione del
comportamento delle strutture.
L’arte del costruire è da ritenersi affidabile, ma ha un limite: è molto
difficile uscire dagli schemi della tradizione costruttiva, risolvere
problemi costruttivi “nuovi” (per funzione o per scala), proporre
soluzioni innovative.
LA SICUREZZA STRUTTURALE
IL CONCETTO DI SICUREZZA STRUTTURALE - 3
La Scienza del Costruire
A parte le esperienze pionieristiche di Hooke ed Eulero fra il XVII ed il
XVIII secolo, è soltanto nel XIX secolo che la MATEMATICA e la
MECCANICA entrano a far parte della pratica progettuale (Mohr e
Clapeyron). L’ARTE DEL COSTRUIRE assurge progressivamente il
ruolo di disciplina scientifica (SCIENZA DEL COSTRUIRE).
Fino agli anni ’50 del XX secolo, la Scienza del Costruire mette a punto
MODELLI DI CALCOLO che supportano l’ingegnere nelle proprie
scelte. Quest’ultime, tuttavia, rimangono ancora fortemente ancorate,
nella pratica, all’ESPERIENZA e alla TRADIZIONE.
CONCEZIONE DETERMINISTICA DELLA SICUREZZA
LA SICUREZZA STRUTTURALE
IL CONCETTO DI SICUREZZA STRUTTURALE - 4
La moderna concezione della sicurezza
Nel corso degli anni ’50 del XX secolo si assiste ad una vera rivoluzione.
Si iniziano a concepire e progettare opere innovative (grattacieli, i ponti
di grande luce, le centrali nucleari…). Gli ingegneri e gli architetti
realizzano che i MODELLI DI CALCOLO fino ad allora impiegati sono,
di fatto, in gran parte giustificati dall’esperienza e dalla tradizione, e
come tali NON SONO GENERABILIZZABILI a nuovi contesti.
Emergono i limiti della SCIENZA del COSTRUIRE:
• i modelli di calcolo offrono una rappresentazione parziale della realtà;
• i parametri che figurano in essi sono affetti da incertezze.
CONCEZIONE PROBABILISTICA DELLA SICUREZZA
LA SICUREZZA STRUTTURALE
IL CONCETTO DI SICUREZZA STRUTTURALE - 5
La moderna concezione probabilistica della sicurezza
Nella concezione moderna della sicurezza, il progetto strutturale è basato
sul CALCOLO DELLA PROBABILITA’ che una struttura soddisfi
prefissati OBBIETTIVI nel corso di assegnati PERIODI DI TEMPO.
Es.: Quale probabilità c’è che la mia struttura sopporti le forze
dell’ambiente (neve e vento e terremoti) senza pervenire a collasso nel
corso nei prossimi 100 anni?
Tutte le moderne normative strutturali sono basate su questo concetto, in
modo più o meno esplicito.
LA SICUREZZA STRUTTURALE
FORMULAZIONE DEL PROBLEMA IN TERMINI PROBABILISTICI
INPUT
FILTRO
OUTPUT
AZIONI
STRUTTURA
RISPOSTA
AZIONI:
FORZE ESTERNE E SPOSTAMENTI IMPRESSI
PARAMETRI DI RISPOSTA:
DEFORMAZIONI, SPOSTAMENTI, TENSIONI, SOLLECITAZIONI.
STRUTTURA FILTRO:
PARAMETRI GEOMETRICI E MECCANICI
LA SICUREZZA STRUTTURALE
FORMULAZIONE DEL PROBLEMA IN TERMINI PROBABILISTICI
INPUT
FILTRO
OUTPUT
AZIONI
STRUTTURA
RISPOSTA
W
K
U
U = U(W,K)
Modello che esprime la risposta in funzione delle AZIONI e delle proprietà della STRUTTURA.
LA SICUREZZA STRUTTURALE
FORMULAZIONE DEL PROBLEMA IN TERMINI PROBABILISTICI
Sia X un vettore che elenca le variabili (elementi di W, K e U) mediante le
quali è possibile confrontare lo stato del sistema con un prefissato STATO
LIMITE. Tale vettore è definito VETTORE DI STATO.
Si definisce SUPERFICIE DI CRISI, e si indica con Lx, lo STATO
LIMITE, o frontiera, che separa lo spazio ω degli stati X in una regione
SICURA ωs ed in una regione INSICURA ωf.
Convenzionalmente, si assume L x ⊂ ωf .
Il problema è generalmente N-dimensionale, essendo N la dimensione di X.
LA SICUREZZA STRUTTURALE
FORMULAZIONE DEL PROBLEMA IN TERMINI PROBABILISTICI
PROBLEMA MONODIMENSIONALE
PROBLEMA BIDIMENSIONALE
X1
ωs
Lx
ωf
ωs
ωf
X
X2
Lx
Es.: Lx rappresenta una resistenza di
un materiale e X la tensione media.
Es.: Lx un limite di spostamento in un
piano, e X1 e X2 sono due componenti
di spostamento di un punto della
struttura.
LA SICUREZZA STRUTTURALE
FORMULAZIONE DEL PROBLEMA IN TERMINI PROBABILISTICI
L’equazione che descrive lo STATO LIMITE Lx può essere in termini
generali espressa come:
f ( X) = 0
dove f è una funzione tale che f(X) > 0 quando X appartiene alla regione
SICURA ωs e f(X) < 0 quando X appartiene alla regione INSICURA ωf.
Si definisce MARGINE DI SICUREZZA il valore assunto da f in
corrispondenza del generico stato X del sistema. La struttura è SICURA nei
riguardi dello STATO LIMITE se M>0 ( X ∈ ωs ). La struttura è INSICURA
se M≤0 ( X ∈ ωf ). M offre una misura della distanza dello stato X dallo stato
limite.
LA SICUREZZA STRUTTURALE
FORMULAZIONE DEL PROBLEMA IN TERMINI PROBABILISTICI
PROBLEMA MONODIMENSIONALE
PROBLEMA BIDIMENSIONALE
X1
ωs
f ( X) > 0
Lx
ωf
X
f ( X) < 0
f ( X) = 0
Es.: Lx rappresenta una resistenza di
un materiale e X la tensione media.
ωs
f ( X1 ,X 2 ) < 0
ωf
f ( X1 ,X 2 ) > 0
X2
Lx
f ( X1 ,X 2 ) = 0
Es.: Lx un limite di spostamento in un
piano, e X1 e X2 sono due componenti
di spostamento di un punto della
struttura.
LA SICUREZZA STRUTTURALE
FORMULAZIONE DEL PROBLEMA IN TERMINI PROBABILISTICI
PROBLEMA MONODIMENSIONALE
PROBLEMA BIDIMENSIONALE
M
M
ωs
Lx
ωf
f ( X) = 0
f ( X) > 0
ωf L x
X
ωs
f ( X) < 0
X1
f ( X1 ,X 2 ) > 0
X2
f ( X1 ,X 2 ) < 0 f ( X ,X ) = 0
1
2
LA SICUREZZA STRUTTURALE
FORMULAZIONE DEL PROBLEMA IN TERMINI PROBABILISTICI
ESEMPIO
d
V
INPUT – AZIONI:
W = (H,V,d,h)
FILTRO - STRUTTURA:
K = (d,h)
OUTPUT - RISPOSTA:
U = U (W,K) = M0 = Vd + Hh
H
h
M0
LA SICUREZZA STRUTTURALE
FORMULAZIONE DEL PROBLEMA IN TERMINI PROBABILISTICI
ESEMPIO
d
V
Sia X = (M0, Mu) il VETTORE DI STATO del sistema.
Sia f(X) = M0-Mu = 0 l’equazione che definisce lo STATO LIMITE.
H
La struttura è SICURA ( X ∈ ωs ) quando M0 < Mu ; la struttura è
INSICURA ( X ∈ ωs ) quando M0 > Mu.
h
Mu
Lx
ωs
ωf
M0
M0
LA SICUREZZA STRUTTURALE
INCERTEZZE ED ALEATORIETA’
Stabilito che, nei riguardi di un prefissato stato limite lo stato X del
sistema può configurarsi in due condizioni reciprocamente
complementari, la SICUREZZA ωs e l’INSICUREZZA ωf, è necessario
prendere coscienza che, in virtù di tutte le incertezze che governano il
problema, l’appartenenza di X a ωs oppure a ωf, è di natura
PROBABILISTICA e non DETERMINISTICA!
LA SICUREZZA STRUTTURALE
PROBABILITA’ DI CRISI ED AFFIDABILITA’
INCERTEZZE FISICHE
SONO RELATIVE ALLA NATURA ALEATORIA DELLE AZIONI W E DEL SISTEMA K E AL LIVELLO
CONOSCITIVO CHE NOI ABBIAMO DI ESSE.
INCERTEZZE SULLE AZIONI:
INTENSITA’
DIREZIONE
PUNTO DI APPLICAZIONE
EVOLUZIONE NEL TEMPO.
INCERTEZZE SULLA STRUTTURA:
VARIABILI
ALEATORIE
PROPRIETA’ MECCANICHE
CARATTERISTICHE GEOMETRICHE
INCERTEZZE STATISTICHE
DIPENDONO ESCLUSIVAMENTE DA CARENZA DI INFORMAZIONI.
INCERTEZZE DI MODELLO
DIPENDONO DALLA CAPACITA’ DEI MODELLI IMPIEGATI DI DESCRIVERE LA REALTA’.
U = U (W,K)
LA SICUREZZA STRUTTURALE
INCERTEZZE ED ALEATORIETA’
Alla luce delle incertezze che contraddistinguono W,K, e U, anche X,
che ne costituisce una selezione, è un VETTORE ALEATORIO. Di
conseguenza, anche il margine di sicurezza M è ALEATORIO.
Nei riguardi di uno stato limite assegnato, l’appartenenza di X alla
regione SICURA ωs o alla regione INSICURA ωf è di tipo
PROBABILISTICO.
Si definisce PROBABILITA’ DI CRISI Pf la probabilità che nel corso di
un intervallo temporale T si verifichi almeno una volta X ∈ ωf, cioè M<0.
Si definisce PROBABILITA’ DI SICUREZZA o AFFIDABILITA’ R la
probabilità che nel corso di T sia sempre X ∈ ωs .
R = 1 − Pf
LA SICUREZZA STRUTTURALE
OBBIETTIVI DELLA PROGETTAZIONE STRUTTURALE
LA PROGETTAZIONE STRUTTURALE DEVE GARANTIRE CHE LA
PROBABILITA’ DI RAGGIUNGIMENTO DEGLI STATI LIMITE DI UNA
STRUTTURA (Pf) SIA MINORE DI UN VALORE ASSEGNATO (Plim):
Pf < Plim
IL VALORE Plim RAPPRESENTA IL LIVELLO DI AFFIDABILITA’
ASSUNTO ACCETTABILE PER LA STRUTTURA
LA SICUREZZA STRUTTURALE
OBBIETTIVI DELLA PROGETTAZIONE STRUTTURALE
PROBLEMI:
• CHI DEFINISCE IL LIVELLO DI AFFIDABILITA’?
(STATO, ENTI NORMATORI…)
• COME SI DEFINISCE IL LIVELLO DI AFFIDABILITA’?
(CONSEGUENZE, RISCHI COMPARABILI, COSTI…)
QUESTE SONO SCELTE DI NATURA POLITICA, ECONOMICA, SOCIALE!
La scelta del livello di affidabilità ottimale, che rappresenta la sintesi delle analisi teoriche e
dell’esperienza acquisita sul costruito, è in genere effettuata in modo da garantire alle nuove
costruzioni un livello di affidabilità non inferiore a quello caratteristico di costruzioni
esistenti, correttamente funzionanti.
LA SICUREZZA STRUTTURALE
METODI DI ANALISI
IL PROCEDIMENTO LOGICO IDEALE
1.
DEFINIZIONE DEGLI STATI LIMITE
2.
MODELLAZIONE PROBABILISTICA DELLE AZIONI (W)
3.
MODELLAZIONE PROBABILISTICA DELLE PROPRIETA’ DEL SISTEMA (K)
4.
DEFINIZIONE DELLE LEGGI CHE ESPRIMONO LA RISPOSTA STRUTTURALE
U = U(W,K))
5.
DEFINIZIONE DELLE PROBABILITA’ DI CRISI O DI SICUREZZA RELATIVE A
CIASCUNO STATO LIMITE PREFISSATO.
6.
VALUTAZIONE DELLA PROBABILITA’ DI CRISI O DI SICUREZZA RELATIVA
A CIASCUNO STATO LIMITE NEL CONTESTO DELLE CONDIZIONI SOCIALI,
ECONOMICHE E POLITICHE AL CONTORNO.
GRANDI DIFFICOLTA’ CONCETTUALI E COMPUTAZIONALI!
LA SICUREZZA STRUTTURALE
METODI DI ANALISI
IPOTESI SEMPLIFICATIVE
IPOTESI SEMPLIFICATIVE GENERALI
•
SI TRASCURANO INCERTEZZE STATISTICHE
•
SI TRASCURANO LE INCERTEZZE DI MODELLO (!!!)
•
LE VARIABILI AFFETTE DA LIMITATE INCERTEZZE FISICHE VENGONO
ASSUNTE DETERMINISTICHE
•
LE VARIABILI AFFETTE DA GRANDI INCERTEZZE FISICHE VENGONO
TRATTATE COME ALEATORIE.
IPOTESI RELATIVE AI SINGOLI PUNTI DEL PROCEDIMENTO
•
ANALISI DI DIVERSO LIVELLO (DA 0 A IV)
LA SICUREZZA STRUTTURALE
METODI DI ANALISI
LIVELLI DI ANALISI
•
IV LIVELLO – ANALISI DI RISCHIO INTEGRALE
•
III LIVELLO – ANALISI AFFIDABILISTICHE
•
II LIVELLO – METODI β
•
I LIVELLO – METODI SEMIPROBABILISTICI
•
LIVELLO 0 – METODI PSEUDODETERMINISTICI
CALIBRAZIONE
LIVELLO NORMATIVO
NELLE ANALISI DI SICUREZZA SI TIENE ANCHE IN CONTO DEGLI ERRORI UMANI!
Gli errori casuali (piccoli errori di calcolo, piccole discordanze tra progetto e realizzazione, …) sono
imprescindibili e vengono tenuti in conto mediante opportuni margini di sicurezza.
Gli errori grossolani (dimenticanza di controventature, inversione ferri parte tesa parte compressa,…)
costituiscono un pericolo latente di estrema gravità.
LA SICUREZZA STRUTTURALE
NORMATIVA ITALIANA
•
METODO SEMIPROBABILISTICO AGLI STATI LIMITE
•
METODO DELLE TENSIONI AMMISSIBILI
IN PROGRESSIVO DISUSO
LA SICUREZZA STRUTTURALE
LA SICUREZZA DELLE COSTRUZIONI ESISTENTI
• QUALE LIVELLO DI AFFIDABILITA’ IMPORRE AD UNA COSTRUZIONE ESISTENTE?
• E SE TALE LIVELLO NON E’ RAGGIUNTO?
• IL CONCETTO DI ADEGUAMENTO E DI MIGLIORAMENTO
• LA PROBLEMATICA RELATIVA AI BENI TUTELATI
LE LINEE GUIDA PER LA RIDUZIONE DEL RISCHIO SISMICO DEI BENI CULTURALI
• L’INTRODUZIONE DELLO STATO LIMITE DI DANNO AI BENI ARTISTICI
• IL SUPERAMENTO DELLA DISTINZIONE TRA ADEGUAMENTO E MIGLIORAMENTO
• IL PROBLEMA DEGLI EDIFICI CON FUNZIONI STRATEGICHE