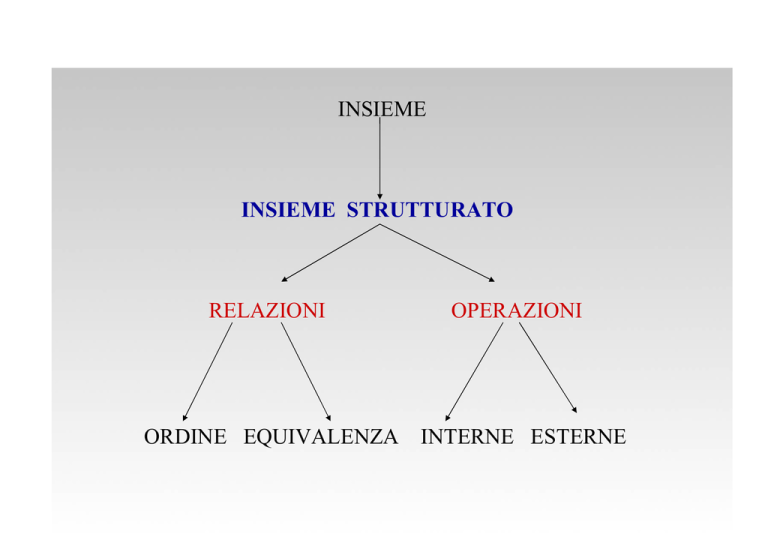
INSIEME
INSIEME STRUTTURATO
RELAZIONI
OPERAZIONI
ORDINE EQUIVALENZA INTERNE ESTERNE
Angela Donatiello
1
Consideriamo l’insieme N dei numeri naturali. N ={0,1,2,3,4,…}
E’ naturale definire in N una somma tra i suoi numeri.
Esiste una corrispondenza tra l’insieme delle coppie di numeri
naturali e l’insieme dei numeri naturali che fa corrispondere alla
coppia (3,6) il numero 9 e alla coppia (7,5) il numero 12.
Una tale operazione è detta
OPERAZIONE INTERNA
all’insieme N
+ : (a , b ) ∈ N × N → a + b ∈ N
N ( + ) è una STRUTTURA ALGEBRICA
Proprietà:
∀x , y ∈ N ⇒ x + y ∈ N
Legge interna:
Proprietà associativa:
∀x , y , z ∈ N ⇒ x + ( y + z ) = ( x + y ) + z
Esistenza dell’elemento neutro:
Angela Donatiello
∀x ∈ N , ∃0 ∈ N | x + 0 = 0 + x = x
2
In N viene però a cadere una proprietà:
Esistenza del simmetrico:
∀x ∈ N, ∃x '∈ N | x + x ' = x '+ x = 0 ?
Tale proprietà viene a cadere in quanto in N nessun elemento è
dotato di simmetrico, eccetto lo zero.
Risulta pertanto necessario ampliare l’insieme N con un nuovo
insieme Z. L’insieme Z è l’insieme dei numeri interi relativi in cui è
possibile definire una somma usuale tra numeri come in N.
+ : (a , b ) ∈ Z × Z → a + b ∈ Z
Z(+) è una STRUTTURA ALGEBRICA
∀x , y ∈ Z ⇒ x + y ∈ Z
Legge interna:
Proprietà associativa:
∀x , y, z ∈ Z ⇒ x + ( y + z ) = ( x + y) + z
Angela Donatiello
3
Esistenza dell’elemento neutro:
Esistenza del simmetrico:
∀x ∈ Z, ∃0 ∈ Z | x + 0 = 0 + x = x
∀x ∈ Z, ∃x '∈ Z | x + x ' = x '+ x = 0
Inoltre:
Se considero due numeri interi relativi qualsiasi a e b, si sa che
a + b = b + a e ciò equivale a dire che la somma tra numeri
gode della proprietà COMMUTATIVA
Angela Donatiello
4
Osserviamo:
• il risultato della composizione di due elementi di Z è ancora un
elemento di Z per cui + è una LEGGE INTERNA a Z
• vale la proprietà ASSOCIATIVA
• esiste l’ELEMENTO NEUTRO
• Ogni elemento di Z ha il SIMMETRICO
•
•
•
Sia G un insieme di natura qualsiasi in cui sia presente una
legge di composizione interna * di natura qualsiasi.
Diremo che G( * ) è un GRUPPO se valgono le tre proprietà
evidenziate in precedenza:
Associatività
Esistenza dell’elemento neutro
Esistenza, per tutti gli elementi, dell’elemento simmetrico
Angela Donatiello
5
Valutiamo Z
(•)
∀x , y ∈ Z ⇒ x • y ∈ Z
∀x , y, z ∈ Z ⇒ x • ( y • z ) = ( x • y) • z
Esistenza dell’elemento neutro: ∀x ∈ Z, ∃1 ∈ Z | x • 1 = 1 • x = x
Legge interna:
Proprietà associativa:
In Z viene a cadere una proprietà:
Esistenza del simmetrico:
∀x ∈ Z, ∃/x '∈ Z | x • x ' = x '• x = 1
E’ vero solo se sia x che x’ sono uguali a 1.
Angela Donatiello
6
A tale scopo risulta necessario definire
m
Q = | m, n ∈ Z ∧ n ≠ 0
n
Q(+ ) è un gruppo abeliano
Q − {0}(•) è un gruppo abeliano e in più vale anche la
proprietà distributiva del prodotto rispetto alla somma
⇒ Q( +,•) è un CAMPO
Angela Donatiello
7
A(+,⋅) anello ⇔ 1) A( + ) gruppo commutativo
2) ⋅ associativa
3) ⋅ distributiva rispetto a +
A(+,⋅) anello commutativo ⇔ 1) A( +,⋅ ) è anello
2) ⋅ commutativa
A( + ,⋅ ) anello unitario ⇔ 1) A( + , ⋅ ) anello
2) ∃ 1 elemento neutro per ⋅
A(+,⋅ ) campo ⇔ 1) A( + ) gruppo abeliano
2) A - {1}(⋅) gruppo abeliano
3) ⋅ distributiva rispetto a +
Angela Donatiello
8
Q è denso: tra due numeri razionali c’è ancora un numero
razionale, ciò nonostante presenta ancora dei “buchi”, ovvero
non è possibile associare ad ogni punto della retta un numero
razionale.
Ad esempio 2 è un numero non razionale, ossia non è possibile
scriverlo sotto forma di frazione. (dimostrazione)
2∉Q
Si considera un insieme R che rispetto alle operazioni di somma e
prodotto è ancora un campo. R ( +,•)
R è denso
R è continuo (la retta reale non presenta “buchi”, ossia è
sempre possibile mettere in relazione biunivoca un punto
della retta con un numero reale)
Angela Donatiello
9
N
N⊂Z⊂Q⊂R
Z
Q
R
INTERVALLI DI R
[a ,+∞[ = {x ∈ R | x ≥ a}
]a ,+∞[ = {x ∈ R | x > a}
]− ∞, b] = {x ∈ R | x ≤ b}
]− ∞, b[ = {x ∈ R | x < b}
[a , b] = {x ∈ R | a ≤ x ≤ b}
[a , b[ = {x ∈ R | a ≤ x < b}
]a , b] = {x ∈ R | a < x ≤ b}
]a , b[ = {x ∈ R | a < x < b}
Angela Donatiello
10
Le slides sono reperibili all’indirizzo web:
http://digilander.libero.it/angeladonatiello/uninsubria.html
Il programma GRAPH con cui sono stati realizzati i grafici
è scaricabile all’indirizzo:
www.padowan.dk
Il programma Maxima (che utilizza Gnuplot per i grafici) è
scaricabile all’indirizzo:
http://maxima.sourceforge.net/
Angela Donatiello
11