( ) MOTO del PROIETTILE

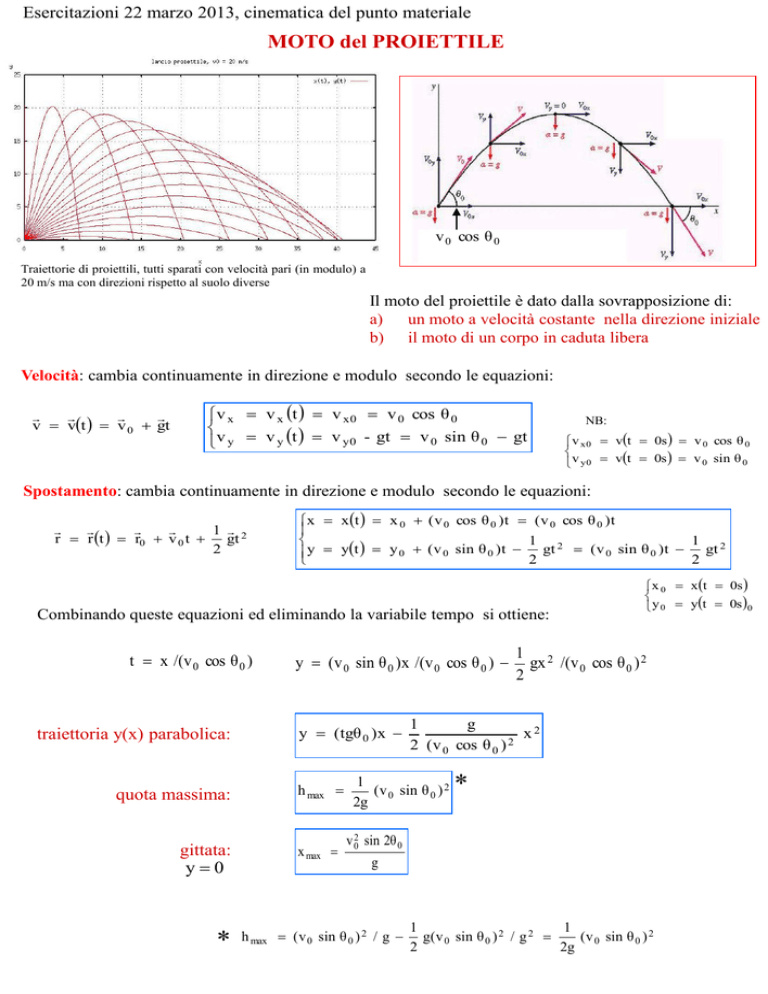
Esercitazioni 22 marzo 2013, cinematica del punto materiale
MOTO del PROIETTILE
v 0 cos θ 0
Traiettorie di proiettili, tutti sparati con velocità pari (in modulo) a
20 m/s ma con direzioni rispetto al suolo diverse
Il moto del proiettile è dato dalla sovrapposizione di:
a) un moto a velocità costante nella direzione iniziale
b) il moto di un corpo in caduta libera
Velocità: cambia continuamente in direzione e modulo secondo le equazioni:




v  vt   v 0  gt
v x  v x t   v x0  v 0 cos θ 0

v y  v y t   v y0 - gt  v 0 sin θ 0  gt
NB:
v x0  vt  0s   v 0 cos θ 0

v y0  vt  0s   v 0 sin θ 0
Spostamento: cambia continuamente in direzione e modulo secondo le equazioni:




1 
r  r t   r0  v 0 t  gt 2
2
x  x t   x 0  ( v 0 cos θ 0 ) t  ( v 0 cos θ 0 ) t


1 2
1 2
y  yt   y 0  ( v 0 sin θ 0 ) t  2 gt  ( v 0 sin θ 0 ) t  2 gt

Combinando queste equazioni ed eliminando la variabile tempo si ottiene:
t  x /(v 0 cos θ 0 )
traiettoria y(x) parabolica:
quota massima:
gittata:
y0
*
y  (v 0 sin θ 0 )x /(v 0 cos θ 0 ) 
y  ( tgθ 0 ) x 
h max 
x max 
x 0  x t  0s 

y 0  yt  0s 0
1 2
gx /(v 0 cos θ 0 ) 2
2
g
1
x2
2 ( v 0 cos θ 0 ) 2
1
( v 0 sin θ 0 ) 2
2g
*
v 02 sin 2θ 0
g
h max  ( v 0 sin θ 0 ) 2 / g 
1
1
g(v 0 sin θ 0 ) 2 / g 2 
( v 0 sin θ 0 ) 2
2
2g
Esercizio1:
Un cannone spara un proiettile alla velocità di 100 m/s ad un certo angolo col piano orizzontale.
a)Si calcoli l’angolo che causa la gittata massima e il valore della gittata.
b)Si calcoli inoltre l’angolo necessario per colpire un bersaglio a 500 m di distanza
a)
 x  v 0 t cos θ

1 2

 y  v 0 t sin θ  2 gt
x

t  v cos θ
0

 
gx 2
sin θ
1
y

x


cos
θ
2 v 02 cos 2 θ



tgθ

y

v0
q
x
y  0
x
 sin θ

gx 2
gx
sin θ
1
1

  0


x


2 cos 2 θ
2 cos 2 θ 
 cos θ
cos
θ
2
2
v
v

0
0


tgθ
Si ha quindi che y=0 o quando x=0 o quando
x 
v 02
g
2 sin θ cos θ 
v 02 sin 2θ
g
Ricordando che la funzione seno è una funzione compresa tra -1 ed 1, si ha che la gittata massima, cioè
xmax si ottiene quando sin(2q )= 1, cioè : 2q = 90° => q =45°
x max 
θ max
v 02
g
 45
45°
b)
d  500m 
v 02 sin 2θ
g
θ 
 gd 
1
arcsin  2 
2
 v0 
 gd 
 9.81  500 ms  2 m 
1
1
1



θ 
arcsin  2  
arcsin 

arcsin 0.49
2
2
2
m 2 s  2 
2
 100
 v0 
1
14,67  14 40 12 
 2 29.37
1
arcsin 0.49  
 
1
2
59.67  5940 12 
 (29  90)
2
Esistono quindi due angoli di inclinazione del cannone per i quali il proiettile partendo con una velocità
pari, in modulo, a 100 m/s colpisce un oggetto a 500 m e sono:
θ  14 4012 
θ  59 40 12
Esercizio2:
Una palla di cannone viene sparata orizzontalmente, alla velocità di 400 m/s, dalla cima di una rupe a
picco sul mare, alta 100 m.
a) In quanto tempo il proiettile cadrà in mare?
b) A quale distanza dai piedi della rupe avverrà l’impatto con l’acqua?
y

v0
Scelgo come origine degli assi la base della rupe
h
x
Poilchè la palla viene sparata orrizzontalmente, cioè ad un angolo q=0° rispetto all’asse dell x, la velocità
in funzione del tempo viene descritta dalle seguenti equazioni
v x  v 0

v y  gt
v x  v x t   v x0  v 0 cos θ 0  v 0  1

v y  v y t   v y0 - gt  v 0 sin θ 0  gt  0  gt
E le equazioni del moto diventano :
x  x t   0  ( v 0 cos θ 0 ) t  v 0 t


1


1
1
 y  yt   h  ( v 0 sin θ 0 ) t  gt 2  h  gt 2



2
2

0

Quando la palla di cannone tocca la superficie del mare y=0 si ha quindi che, se t1 è l’istante in cui la
palla raggiunge il mare si può scrivere:
x 1  x t 1   v 0 t 1


1 2
 y1  yt 1   0  h  2 gt 1

1 2
gt  h
2 1
t1 
2h

g
100 m  s 2


9.8
m
10 s 2  3.1 s
Trovato l’istante in cui la palla raggiunge il mare sostituisco il suo valore nell’equazione che descrive il
moto lungo x per trovare a che distanza dai piedi della rupe la palla cade in acqua.
x 1  x t 1   v 0 t 1  v 0 
2h
 400 m s  3.1 s  1200m  1.2Km
g
Esercizio3:
Da una macchina da allenamento alta 1.70 m viene lanciata orizzontalmente una palla da baseball con
v0= 161 km/h verso il battitore posto a d =18.3 m.
1) Calcolare il tempo necessario a percorrere d/2
2) Calcolare il tempo necessario a percorrere il restante cammino (d/2)
3) Calcolare la coordinata verticale della palla rispetto a quella iniziale quando la coordinata orizzontale
è d/2
4) Calcolare la coordinata verticale della palla rispetto a quella iniziale quando la coordinata orizzontale
èd
Risposta alla domanda n. 1: 0.205 s
Risposta alla domanda n. 2: 0.205 s
Risposta alla domanda n. 3: 1.49 m
Risposta alla domanda n. 4: 0.88 m
Scelgo il sistema di riferimento con l’origine posto
ai piedi della macchina da allenamento
t=to= 0s
t=t1
t=t2
y
1.7 m
x
d=18.3 m
Le equazioni che descrivono il moto della palla sono:
 161 km h
v
Velocità:  0 x
v 0 y  0

v x t   v 0 x


v y t   v 0 y  gt
 161 km h  44.7 m s
 9.8 m s 2  t
x t   x 0  v 0 x t  161 km h  t


1 2
2
2
yt   y 0  2 gt  1.7m  9.8 m s  t

 x 0  0m
Eq. moto: 
y 0  1.7m
1) t1=?
xt   x 0  v 0 x t

xt 1  
d
 v 0x t 1
2

t1 
d
18.3m

 0.205s
2v 0 x
89.4 m s
2) t2 -t1=?
xt   x0  v0 xt

xt2   d  v0 xt 2


3) y(t1)=?
yt   y 0 
t2 
1 2
gt
2

yt 1   1.7m 
d
18.3m

 0.41s
v0 x 44.7 m s
t2  t1  0.41s  0.205s  0.205s
9.8  0.2052
m  1.70m  0.21m  1.49m
2
4) y(t2)=?
1
y  y 0  gt 2
2

yt 2 
9.8  0.412
 1.7m 
m  1.70m  0.82m  0.88m
2
Esercizio4:
In un fiume largo 500 m, una barca a motore si dirige da una riva, con una velocità di 7.2 Km/h, in direzione
perpendicolare alla riva stessa. La corrente però la fa approdare sull’altra riva a 150 m più a valle. Trovare la
velocità della corrente ed il tempo totale di attraversamento del fiume
Composizione di due moti indipendenti, che durano però uno stesso tempo totale T. Pertanto:
x A  0

y A  0
x B  d  150m

 y B  s  500m
d
y
fiume
v x  v Ax  v fiume

v y  v Ay  7.2 km h  2 m s
s
A
x


x t   x A  v x t
x B  x T   d  v x T
 


 y B  yT   s  v y T
 yt   y A  v y t

La velocità della corrente è quindi:
B
vx 
Da cui si ricava:
d
150m

v x  T  T

d
500m

 250 s  4 min e 10 s
T 
vy
2ms

d
150m

 0.6 m s
T
250s
Il tempo totale di attraversamento è invece T=4 min e 10 s
Esercizio1:
Un corpo si muove dimoto circolare uniforme con periodo T = 2.00s e r =3.00m. Ad un certo istante la
sua accelerazione è a  6î  4 ĵ
 
va
1) Calcolare
 
r a
2) Calcolare
v
j
i
3) Calcolare il modulo di v
4) Calcolare il vettore v nello stesso istante
a
1)
v ┴ a quindi il prodotto scalare è nullo
(il prodotto scalare tra due vettori ortogonali è identicamente uguale a 0)
2)
r // a quindi il prodotto vettoriale è nullo
(il prodotto vettoriale tra due vettori paralleli è identicamente uguale a 0)
3)
v  ωr 
2π
2  3.14
r 
3.00 m s  9.42 m s
T
2.00
4) Poichè v ed a sono perpendicolari e quindi il loro prodotto scalare sarà nullo si ha:
 
3
a  v  a x v x  a y v y  6v x  4v y  0  v y 
vx
2
Inoltre poiché v2=vx2+vy2
2
9
13 2
v  v 2  9.42 m s 2  v 2x  v 2y  v 2x  v 2x 
vx
4
4
4 2
4
9.42 m s 2  27.3 m 2 s 2 
 v 2x 
v 
v x  5.22 m s
13
13
vy 

v  v x î  v y ĵ  5.22m î  7.83m ĵ
3
3
vx 
5.22 m s  7.83 m s
2
2
Esercizio2:
Trovare la velocità angolare nei seguenti casi:
a)La terra che ruota intorno al sole
b)La terra che ruota intorno a se stessa
c)La lancetta delle ore
d)La lancetta dei minuti
e)La lancetta dei secondi
2π
2π

 2.0  10  7 rad s
a) ω1 
T1
b) ω 2
365  24  60  60 s
NB :
2π
2π


 7.3  10  5 rad s
T2
24  60  60 s
c) ω 3 
2π
2π

 1.45  10  4 rad s
T3
12  60  60 s
d) ω 4 
2π
2π

 1.7  10  3 rad s
T4
60  60 s
180  π  3.14 rad
1rad 
180
 57 ,3
π
e) ω 5  2π  2π  0.1 rad s
T5
60 s
Esercizio 3:
Determinare la velocità e la velocità angolare che deve mantenere un aereoplano affinchè il sole appaia
fisso all’orizzonte
L’aereo deve volare verso est o verso ovest? (NB: RT= 6.37∙103 Km)
ω aereo  ω terra  7.3  10 5 rad s (vedi esercizio precedente)
Il segno “-” sta ad indicare che l’aereo deve andare da est verso ovest
(verso contrario a quello della rotazione terrestre)
Ovest
v aereo  ω aereo  R T  7.3 
10 5
rad s  6.37 
10 3
Km  4.65 
Est
10 2
m s  1670 Km h
Esercizio4:
Un treno, affrontando una curva di raggio 150 m, nei 15 s che impiega a percorrere la curva rallenta da
90Km/h a 50Km/h. Calcolare l’accelerazione tangenziale e centripeta nel momento in cui la velocità è
50Km/h, assumendo che il treno continui a decelerare
1. Trasformiamo da Km/h a m/s:
t1,v1
90
v1  90 Km h 
v2
m s  25 m s
3.6
50
 50 Km h 
m s  14 m s
3.6
2. Calcoliamo l’accelerazione tangenziale media tra i 15 s in esame:
at 
R=150m
v  v1
14  25 m s  0.7 m s 2
Δv
 2

Δt
t 2  t1
15s
3. Calcoliamo l’accelerazione radiale all’istante in cui v=v2:
ac 
t2,v2
v 22
R

142
m2 s2
 1.3 m s 2
150m
4. Calcoliamo il modulo dell’accelerazione nell’istante in cui v=v2:

a  a 
a 2t  a c2 
 0.72
 1.3 2 m s 2  1.5 m s 2
NB: Se il treno non continuasse
decelerare e continuasse però
seguire la stessa traiettoria curva,
avrebbe: a t  0

a 
a
a
si
ac
Esercizio5:
Un bambino siede a 4m dal centro di una giostra che compie un giro completo ogni 10s. Qual’è
l’accelerazione del bambino?
Moto circolare uniforme => abbiamo solo accelerazione centripeta.
a c  ω2 R
Sapendo che il periodo T di rotazione della giostra è 10s, possiamo ricavarci la velocità angolare w:
ω 
2π
6.28rad

 0.63 rad s
T
10s
L’accelerazione del bambino, che siede ad una distanza R=4m dal centro di rotazione è quindi:
a c  ω 2 R  0.63 rad s2  4m  0.40 rad 2 s 2  4m  1.6 m s 2
Esercizio6:
Un aereoplano da caccia a reazione che vola alla velocità di 500 m/s esce da una picchiata percorrendo
una traiettoria circolare. Qual’è il raggio della traiettoria se il pilota è soggetto ad una accelerazione di
5g?
ac 
R 
v2
R
5  10 2
5g
R 
m s
2

v2
v2

ac
5g
2.5  10 5 m 2 s 2
 5.1  10 3 m  5 .1Km
2
5  9.8 m s
ac=5g
R=?
v