Astronomia
2016-17
Parte III
Evoluzione stellare
16
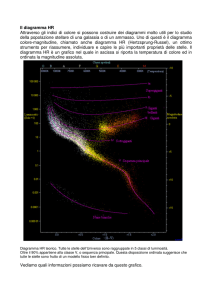
Evoluzione sul diagramma HR
Stella con massa M ≈ M ⊙
Red giant
Main sequence
Subgiant
Evoluzione stellare
Oltre la Sequenza principale
Evoluzione del nucleo nella fase di Gigante Rossa
8
Stelle M > 0.5M ⊙ : contrazione del nucleo, T ≈ 10 K
Innesco della reazione 3α
Come per l'accensione H, anche l'accensione He dipende dallo stato di
degenerazione della materia del nucleo
Dipende dalla massa della stella
M < 0.5M ⊙
La pressione degli elettroni degeneri ferma il collasso del nucleo prima
dell'accensione del He
0.5M ⊙ < M < 2.25M ⊙
3-α si accende in un nucleo dominato da
pressione degenere
Estrema dipendenza dell’innesco
della 3-alpha dalla temperatura
ε 3α ∝ ρ 2T 40
L'accensione dell’He è esplosiva
“Helium Flash”
La pressione degli elettroni
2
5/3
P
≈
0
.
05
(
h
/
m
)
n
e
e
degeneri non dipende da T
In un gas non degenere: produzione energia
aumento della pressione
espansione rallentamento della reazione
M > 2.25M ⊙
L'elio si accende nel nucleo non degenere, in modo non esplosivo
Evoluzione sul diagramma HR
Stella con massa M ≈ M ⊙
• Flash dell'elio
T cresce
Si ferma quando T rimuove la degenerazione degli elettroni
4π 2 me kT
nQ ≈
2
h
3/ 2
Nucleo:
non degenere, convettivo,
in espansione
• Dopo una fase di assestamento:
He
C,O in nucleo non degenere
H
He in uno strato circostante
- Il guscio di H che fonde in He (che fornisce la
maggior parte dell'energia) si è assottigliato:
La luminosità diminuisce
- Espansione del nucleo, contrazione dell'inviluppo
La T cresce leggermente
• La stella si trova nella zona del “braccio orizzontale” del diagramma HR
Evoluzione sul diagramma HR
Stella con massa M ≈ M ⊙
• Diagramma HR: “horizontal branch” (braccio orizzontale)
Nel braccio orizzontale
•La posizione precisa dipende dalla
massa perduta nella fase di gigante
Helium flash
•Più massa perde la stella, meno
inviluppo circonda il nucleo, e più la
superficie della stella è calda
Evoluzione sul diagramma HR
Stella con massa M ≈ M ⊙
• Quando anche He si esaurisce, il nucleo si contrae
Nucleo di C e O (degenere)
Due shell concentriche (H He, He C) continuano a dare energia
• L'inviluppo si dilata
La stella evolve con L∼costante fino al limite di Hayashi
• Si instaura la convezione. La stella diventa molto luminosa con T ∼ costante
“Ramo asintotico”
La convezione può portare alla superficie il C dal nucleo
“Dredge-up”
Stelle di classe spettrale R ed N, ricche di Carbonio
In stelle di massa solare il C non arriva ad accendersi
Il bruciamento dell‘He nello strato interno diventa instabile
• Quando la stella raggiunge la sommità del braccio asintotico:
”Supergigante rossa”
RSG ~ 300 RS
• Grande perdita di massa massa, fino a perdere tutto l'inviluppo
Inviluppo: Nebulosa planetaria
Nucleo: molto caldo e degenere, di C e O,
privo di reazioni termonucleari: Nana Bianca
Evoluzione sul diagramma HR
Stella con massa M ≈ M ⊙
Il nucleo di C e O diviene completamente degenere
Evoluzione sul diagramma HR
Stella con massa M ≈ M ⊙
Nebulosa planetaria
GM 2
• Espansione degli strati esterni, debole legame gravitazionale U GR = −
R
• In competizione con il trasferimento di momento dei fotoni p = E / c
- Espansione: evidenza spettroscopica
Redshift
- Forma anulare: profondità ottica ai
bordi della “bolla”
Righe mostrano doppio spostamento
Doppler (blueshift + redshift)
vshell ≈ 10 − 50 km/s
Tshell ≈ 10 4 K
osservatore
Blueshift
Linea di vista
Linea di vista
M shell ≈ 0.1M Sun
osservatore
Materiale disponibile per successive
generazioni di stelle
Abell 39
Ring Nebula (M57)
Colstellazione Lyra
Distanza ∼ 1kpc
Diametro ∼ 0.3pc
Eskimo
2392)
MedusaNebula
nebula(NGC
(Abell
21)
Old planetary nebula
Evoluzione sul diagramma HR
Stella con massa M ≈ M ⊙
Tempi scala
104
yrs
109 yrs
1010 yrs
1010 yrs
Evoluzione sul diagramma HR
Stella con massa M ≈ M ⊙
LPN
PN = fase di
massima luminosità
nella vita di una
stella
I valori massimi di
luminosità nella
classe PN hanno
limite superiore ben
definito
(stelle di massa
superiore a una
certa soglia
evolvono
diversamente)
Nebulose planetarie come indicatori di distanza
PNe nella galassia di Andromeda (M31)
Funzione di Luminosità (LF)
La LF cade bruscamente, individuando
una luminosità massima ben precisa
Merrett et al. (2006)
Usando nebulose planetarie:
DVirgo / DM 31 = 20.65 ± 6%
Approcci simili (LF cut-off) usati con altre classi di oggetti, e.g.:
• Supergiant stars
• Dominant Galaxy in clusters
Evoluzione sul diagramma HR
Stella con massa M ≈ M ⊙
La stella è divenuta una nana bianca
Sostenuta unicamente dalla pressione degli elettroni degeneri
Valori tipici di: Dimensione, densità, pressione?
Raggio:
R ∝ L1/ 2T −2
L ∝ R 2T 4
TWD ≈ T⊙
LWD ≈ 10−4 L⊙
RWD ≈ 7 ×108 cm
RWD / R⊙ ≈ 10−2
Densità:
ρ WD
Pressione:
≈ 0.05 ⋅
(2 × 1033 g)
6
3
=
≈
10
g/cm
(4π / 3)(7 × 108 cm)3
ρ
2 Z
P ≈ 0.05 ⋅ h
A m p
5/3
−27
5/3
1
me
5/3
(6.63 ×10 erg ⋅ s)
10 g/cm
22
2
0.5
-28
−24 ≈ 3×10 dyn/cm
9.11× 10 g
1.67 × 10 g
2
6
3
Nana bianca
RWD / R⊙ ∝ ( LWD / L⊙ )1/2 ≈ 10−2
RWD ≈ 7 ×108 cm
Noto con grande precisione
Dalla massa (sistema bunario) si ricava il raggio in modo accurato
Evoluzione stellare
Nana bianca
• Relazione tra massa e raggio di una nana bianca
Z
P ≈ 0.05 ⋅ h 2
A
5/3
ρ
mp
5/3
1
me
GM 2
P≈
R4
2
Pressione necessaria
dP
GM (r )
=−
ρ
(
r
)
all’equilibrio gravitazionale
dr
r2
GM
2 Z
≈
0.05
⋅
h
R4
A
5/3
1
m p
Z
GM 2−(5/3) R −4+5 ≈ 0.05 ⋅ h 2
A
h
M R ≈ 0.05 ⋅
Gme
2
1/3
Regime non-relativistico
5/3
1 M
me 4 R 3
1
4
m
p
5/3
ρ ≈ M / 4R3
5/3
1
me
5/3
5/3
1
4m p
5/3
M
M
⊙
Z
A
Z
R ≃ 1.2 × 10 9 cm
A
5/3
− 1/3
Nota la massa per una nana
bianca (e.g. sistema binario),
il suo raggio è precisamente
determinato
Per una massa maggiore si ha un raggio inferiore
Evoluzione stellare
Nana bianca
Per WD di massa sufficientemente grande il gas tende a diventare relativistico
Conseguenza nella relazione massa-raggio?
Caso non-relativistico
Pdeg,non-rel
3
=
π
2/3
h2
Z
20m 5/3
m
p
e A
Caso ultra-relativistico
5/3
ρ
1/3
5/3
Pdeg,rel
Pdeg ∝ ρ (4+ε )/3
hc Z
3
=
4/3
π 8m p A
4/3
ρ 4/3
Per masse crescenti si passa dal
regime non-rel a ultra-rel ε: 1 → 0
Che cosa succede al raggio della stella sostenuta da pressione degenere?
(4 +ε )/3
GM 2
(4 +ε )/3
M
Peq ≈
∝ρ
= (4+ε )
4
R
R
pressione interna necessaria
a sostenere la stella
R∝M
ε
R ∝M
ε −2
3ε
4 +ε
−2
3
ε →0
=M
ε −2
3
R → M −∞ → 0
(Gas ultra relativistico)
Se si raggiunge la pressione ultrarelativistica:
La pressione degenere non è più in grado di supportare la gravità
La stella collassa (limite di Chandrasekhar)
Evoluzione stellare
Nana bianca
• Relazione tra massa e raggio di una nana bianca
R∝M
− 1/3
Regime non-relativistico
Regime relativistico
ε −2
3ε
R∝M
ε →0
R→0
Massa di
Chandrasekhar
Nessuna nana bianca può avere massa superiore alla
massa di Chandrasekhar
Nana bianca:Temperatura superficiale
Temperatura superficiale
λmaxT ≃ 0.29 cm K
White Dwarf G191-B2B spectrum
Ly γ
Ly β
0.29
K
−5
10
≃ 29, 000 K
Lyman-series lines
T≃
Ly α
Per una nana bianca
appena formata:
Artifact
T ≈ 5 × 104 K
(iniziale)
Picco di emissione: UV
10-5 cm
I fotoni ionizzano gli strati esterni espulsi:
Nebulosa planetaria
Raffreddamento:
Nana bianca più fredda conosciuta: WD 0346+246,
T ≈ 3900 K
Evoluzione stellare
Nana bianca
Interno della stella:
Nessuna reazione nucleare in atto, gas degenere
• Bassa opacità
fotoni non facilmente assorbiti da gas degenere
• Alta conducibilità termica
Basso gradiente termico
elettroni liberi nel gas degenere
T ∼ 107-108 K
Effetto Zeeman
Campi magnetici ∼ 105 - 107 Gauss
Gas degenere
(0.99 R)
La stella irraggia e si raffredda
Processo lentissimo:
Gas non-degenere, T ∼ 104 K (0.01 R)
Riserva termica a ~107K
Irraggia come corpo nero a ~104K
Fotosfera: Minore conducibilità termica
Rallenta il raffreddamento
WD: Estremamente deboli nel visibile
Spesso osservate come compagne in sistemi doppi
Evoluzione sul diagramma HR
Tempo di raffreddamento delle nane bianche
Energia persa = luminosità
L = 4πR σT
2
ETh ≈
4
dETh
=
dt
dETh M dT
≈
k
dt
mP dt
M
kT
mP
M dT
k
mP dt
M
k
1
dt =
dT
2
4
mP 4π R σ T
1
kM
−3
tWD ≈
T
3 4π R 2σ mP
4πR 2σT 4 =
Nane bianche
utilizzate
come
indicatori
dell’età
dell’universo
tWD
1
(1.4 ×10 −16 erg K -1 )(1033 g)
−3
≈
T
12π (6 ×108 cm) 2 (5.7 × 10 −5 erg cm -2s -1K -4 )(1.7 × 10 − 24 g)
≈ (3 × 1018 yr K 3 )T −3 = (3 × 109 yr)(103 K )3 T −3
tWD
T
≈ (3 × 109 yr) 3
10 K
−3
Luminosità in funzione del tempo:
T ∝ t −1/3
L(t ) ∝ R 2T 4 ∝ t −4/3
L ∝ T 4 ∝ t −4/3
White dwarfs as cosmic clocks
Cooling of white dwarfs
Globular cluster M4
White dwarf luminosity scales and age
(and with mass) as:
tWD
T
≈ 3 × 10 yr 3
10 K
−3
9
More detailed models give:
T ∝ t −1/3
L ∝ T 4 ∝ t −4/3
L(t ) ∝ Mt −7/5
L( M , t ) ∝ Mt −7/5
Hansen & Liebert (2004)
Luminosity function of WD as indicator
of population age
Simulazione dell’evoluzione stellare sul diagramma HR
(Geneva Stellar Model)
Stelle di massa solare
Evoluzione di una stella di 1
massa solare
Evoluzione delle stelle
2.25M ⊙ < M < 8M ⊙
Differenza rispetto a M ≈ M ⊙
L‘He viene acceso nel nucleo non degenere, non si verifica il “flash”
Per il resto la stella evolve in modo simile
alle stelle di massa minore:
- il nucleo di C ed O si contrae e diventa degenere
- l'inviluppo si espande finché la stella raggiunge il
ramo asintotico
Attorno al nucleo si formano due strati di
combustione: H
He, He
C
La T non è sufficiente a fondere il C
Forte vento stellare
Lifetime: tstar ∝ M
intero inviluppo espulso come nebulosa planetaria
−2.5
tstar
t⊙
M star
≃
M
⊙
Consideriamo ad esempio:
M star ≃ 5M ⊙
8
tstar ≃ 5−2.5 × 1010 yr ≈ 10 yr
−2.5
Time-scales (M = 5Msun)
Prialink stellar model
H-burning
9.4 x 107 yrs
1
Expansion
4.6 x 105 yrs
0.005
He-burning
1.6 x 107 yrs
0.17
Evoluzione stellare sul diagramma HR
M > 8M ⊙
Stelle più massicce di 8 Msun
T sufficienti a bruciare il C
E elementi più pesanti per stelle di massa crescente
Bruciato il C si passa al Ne, O, Si, … Fe (alpha process); quindi: r, s process
Ogni volta che termina un bruciamento il
nucleo si contrae e l'inviluppo si espande
• L’interno si comprime, aumentano P e T
nel nucleo (gas perfetto)
Aumento della pressione di radiazione
(Stefan-Boltzmann)
• La pressione spinge all’esterno gli
strati superficiali: espansione
Espansione nucleo,
contrazione inviluppo
Accensioni:
C
He
H
Contrazione del nucleo,
espansione inviluppo
T superficiale diminuisce
Viceversa:
A ogni inizio di nuovo bruciamento il nucleo
si espande e l'inviluppo si contrae
T superficiale aumenta
La stella traccia sul diagramma HR una traiettoria che va “avanti e indietro”,
con L circa costante
La fase finale delle stelle massicce
M > 8M ⊙
Il nucleo viene circondato da strati di bruciamenti successivi, formando una
“struttura a cipolla”
10−2 R⊙
Bruciato anche il 28Si e 32S
si forma un nucleo ferroso
(56Fe, 58Ni)
103 R⊙
Non c'e più convenienza
energetica a fondere 56Fe e
58Ni in elementi più pesanti
Densità estreme nel nucleo:
ρ core ≃ 109 g cm -3
Time-scales (M = 15Msun)
Geneva model
H-burning
He-burning
Carbon
Oxygen
Silicon
1 x 107 yrs
1 x 106 yrs
4 x 102 yrs
1 yr
10-2 yrs
1
0.1
4x10-5
10-7
10-9
Geneva model of stellar evolution
Relazione massa-lifetime
t* ∝ M −2.5
di massa fino a ≈ 10M ⊙
La relazione
Evoluzione stellare sul diagramma HR
vale per stelle
(Tempo di permanenza nella MS)
(107yr)
X=
mH
mTOT
Y=
mHe
mTOT
Metallicità:
Z=
(4x107yr)
(2x108yr)
(6x108yr)
mmetals
mTOT
(4x109yr)
(1010yr)
Per stelle super-massive (M > 30Ms):
t* → tm ≈ 3 × 106 yr
Meynet et al. 1993 (Astr. & Astr. Supp. Ser., 98,477)
Simulazione dell’evoluzione stellare sul diagramma HR
(Geneva Stellar Model)
Stelle intermedie
Evoluzione di otto stelle da 1 a 8
masse solari
Composizione finale di una stella con massa 25 Msun
up to He
burned
up to H-burned
up to O
burned
Mass fraction
up to Si
burned
up to Ne-burned
(pre-Supernova)
Interior mass (MSun)
unburned