Moto Parabolico
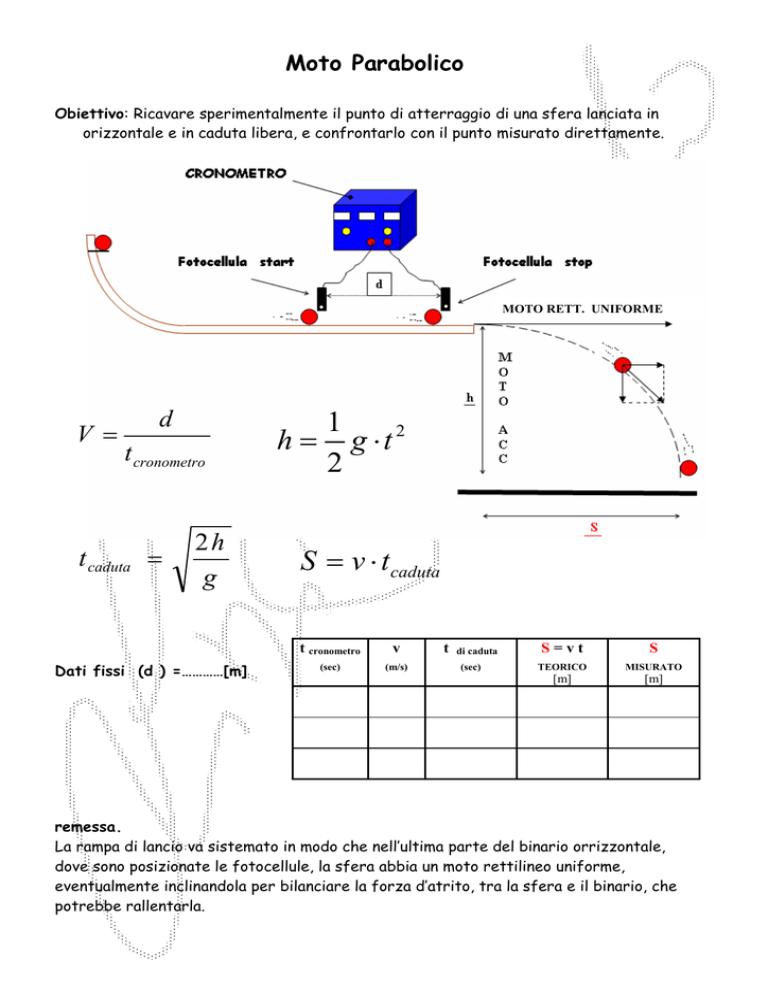
Obiettivo: Ricavare sperimentalmente il punto di atterraggio di una sfera lanciata in
orizzontale e in caduta libera, e confrontarlo con il punto misurato direttamente.
MOTO RETT. UNIFORME
V=
d
t cronometro
t caduta =
2h
g
Dati fissi (d ) =…………[m]
1
h = g ⋅t2
2
S = v ⋅ t caduta
t cronometro
v
(sec)
(m/s)
t
di caduta
(sec)
S=vt
S
TEORICO
MISURATO
[m]
[m]
remessa.
La rampa di lancio va sistemato in modo che nell’ultima parte del binario orrizzontale,
dove sono posizionate le fotocellule, la sfera abbia un moto rettilineo uniforme,
eventualmente inclinandola per bilanciare la forza d’atrito, tra la sfera e il binario, che
potrebbe rallentarla.
Nota :
Lo spazio S è in relazione alla velocità che ha il corpo all’uscita dal binario (moto
rettilineo uniforme), ed al suo tempo di caduta (moto uniformemente accelerato).
Dal momento che la sfera esce dal binario. La direzione del moto non è più rettilineo, in
quanto viene ad agire una forza costante ( Forza di gravità ) che provoca un moto
uniformemente accelerato con direzione verticale verso il basso. A questo punto la
traiettoria diventa una parabola .
La sfera infatti e sottoposta a due moti, uno rettilineo uniforme orizzontale, dovuto
all’impulso iniziale e l’altro uniformemente accelerato verticale, dovuto all’azione costante
della forza di gravità.
Sapendo l’altezza della sfera da terra, con la formula della legge oraria posso ricavarmi il
tempo di caduta.
Potendo calcolare la velocità di uscita dal binario, e il tempo di caduta, posso ricavare
teoricamente lo spazio in orizzontale che può percorrere durante il volo.
Fasi operative:
• Posizionare le fotocellule ad una distanza misurata, e mettere a terra, in
corrispondenza dell’eventuale punto di impatto della sfera sul pavimento, un
cartone che si deformerà nel punto di caduta.
•
Azzerare il cronometro e posizionare la sfera sullo scivolo che gli darà l’impulso
iniziale.
•
Lasciare la sfera che incomincerà a scivolare lungo il percorso attraversando le
fotocellule, che comandano il cronometro, a velocità costante.
•
Con il tempo del cronometro e lo spazio tra le fotocellule si ricava la velocità
d’uscita.
•
Con l’accelerazione di gravità e lo spazio di caduta si ricava il tempo di volo.
•
Con la velocità orizzontale e il tempo di volo si calcola sperimentalmente il punto di
caduta rispetto la verticale della fine del binario.
•
Con un metro si misura direttamente la distanza in orizzontale percorsa dalla
sfera durante il volo. Si confrontano i dati sperimentali, teorici e pratici, che
dovrebbero coincidere tenendo conto degli errori possibili.












