LICEO SCIENTIFICO STATALE “G.B. GRASSI”
CLASSI PRIME 2013/14
INDICAZIONI DI LAVORO PER LA
SOSPENSIONE DEL GIUDIZIO IN FISICA
Liceo scientifico e liceo delle scienze applicate
In relazione alle esigenze del secondo anno di corso, si segnala la necessità di una soddisfacente
conoscenza dei contenuti del programma di seguito indicato; durante il periodo estivo dovrai rivedere
con attenzione sia la teoria che la sua applicazione, tramite lo svolgimento di esercizi e problemi.
Poniti l’obiettivo di assimilare i contenuti indicati, curando con particolare attenzione il linguaggio
utilizzato e la chiarezza dell’esposizione. Oltre al manuale di fisica (G. Ruffo, Fisica Lezioni e problemi,
Zanichelli), ti servirai del materiale che trovi sul sito del liceo.
Ad inizio settembre dovrai sostenere una prova scritta (sugli argomenti indicati, durata un’ora e
mezza) per stabilire se hai colmato le lacune nella tua preparazione.
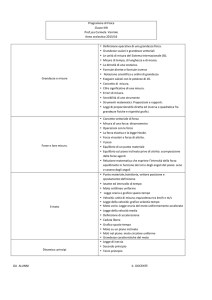
PROGRAMMA
1. Introduzione alla fisica ed elementi di base di matematica
Di che cosa si occupa la fisica? Costruzione grafici (anche con Excel). Gli errori nei grafici. Proporzionalità diretta e
dipendenza lineare. Potenze di dieci. Formule inverse.
2. La misura delle grandezze fisiche
Il linguaggio dei numeri (la notazione scientifica, l’ordine di grandezza di un numero, l’arrotondamento di un numero).
Misurabilità di una grandezza. Misure dirette e misure indirette. Il concetto di unità di misura, scelta dello strumento e
del campione. Errori di misura. Errore connesso ad ogni misura, tipi di errore. Misurazioni eseguite una sola volta.
Misurazioni ripetute alcune volte (media e semidispersione massima). Cenni alla nascita ed all’evoluzione nel tempo
dei sistemi di unità di misura. Il Sistema Internazionale di unità di misura, SI. Unità fondamentali e unità derivate del SI.
Il calibro a cursore. L’errore connesso alla misura con uno strumento preciso; caratteristiche di uno strumento di
misura. La propagazione degli errori nelle misure indirette. Cifre significative. Notazione esplicita e notazione implicita
dell’errore.
Le grandezze fisiche. La misura di lunghezze, aree e volumi. La misura della massa. Misure di densità.
3. I vettori
Grandezze scalari e grandezze vettoriali. Un esempio di vettore: lo spostamento. Definizione di vettore. Elementi di
calcolo vettoriale: somma di vettori (metodi punta-coda e del parallelogramma), prodotto di un vettore per uno
scalare, vettore opposto di un vettore dato, differenza di due vettori, scomposizione di un vettore lungo due direzioni
assegnate; versori, notazione cartesiana di un vettore.
4. Il moto
Grandezze cinematiche: posizione, spostamento, velocità. Scelta del sistema di riferimento e ruolo delle condizioni
iniziali. Formulazione cinematica del principio di inerzia, sistemi di riferimento inerziali. Relatività del moto, principio di
relatività. Il “gran navilio” di Galileo. La cinematica del moto rettilineo uniforme: velocità media e velocità media
scalare, equazione oraria, diagramma orario, legge della velocità e relativi grafici. Moto rettilineo uniforme a tratti: dal
grafico (s-t) al grafico (v-t) e viceversa. Radianti. Moto circolare uniforme: definizione di periodo, frequenza, velocità
angolare, velocità tangenziale. Accelerazione centripeta.
5. Le forze
Le forze cambiano la velocità. La misura delle forze. La forza peso. La forza elastica. La forza d’attrito. Equilibrio del
punto materiale. L’equilibrio su un piano inclinato.
6. L’equilibrio dei fluidi
Pressione. La pressione nei liquidi. Principio di Pascal e legge di Stevin. La spinta di Archimede. Misura della pressione
2
atmosferica. Diverse unità di misura della pressione e relativi fattori di conversione (atm, bar, mbar, mmHg, kgP/cm ).
1
Materiale di riferimento: dal libro di testo:
Nelle pagine segnalate ci sono numerosi problemi svolti. Esaminali con particolare attenzione!
Dopo aver studiato la teoria, esamina con attenzione anche le pagine Per collegare le idee alla fine di ogni unità
PARTE A
Pagine A7, A11, A15, A19, A23, A27, Test e quesiti online (richiamo a pag. A31), A33 n. 10-11-12-15, A34, A36, A38,
A39, A59, A64, A69, A73 (tranne 8 e 9), A77 (tranne 14-15 e 16), A81, A85, A89, A97, A98, A100, A101, A102, Problemi
riassuntivi (richiamo a pag. A102)
PARTE B
Pagine B5, B19, B25, B26, B27, B35, B39, B45, B49, da B53 a B58.
PARTE C
Pagine C5, C9, C26 n.1-2-3, C28, C29, C30 n. 14-15-16, C40, C41, C54, C55
PARTE D
Pagina D5
Altro materiale:
La misura delle grandezze fisiche.
3
1.Il litro serve a misurare il volume? Appartiene al SI? A quanti m corrisponde?
2.Un giradischi a 45 giri/minuto ha compiuto 18 giri. Quanti secondi sono passati?Quanti giri farà nello stesso tempo
il piatto di un giradischi a 33 giri/minuto?
3.Trasformare:
a. 15 μs in megasecondi, millisecondi, terasecondi;
-12
-3
-18
[15·10 Ms; 15 ·10 ms; 15·10 Ts]
b. 1500 km in millimetri, in picometri, in attometri, in petametri;
9
15
24
-9
[1,5 ·10 mm; 1,5 ·10 pm; 1,5 ·10 am; 1,5·10 Pm]
c. 1,32 Gg in kilogrammi, in milligrammi, in megagrammi, in exagrammi;
6
[1,32·10 kg; 1,32·1012 mg; 1,32·103 Mg; 1,32·10-9 Eg]
4.Trasformare:
2
a. 1234 dm in megametri quadrati, in micrometri quadrati, in kilometri quadrati;
-11
2
13
2
-5
2
[1,234·10 Mm ; 1,234·10 μm ; 1,234·10 km ]
3
b. 350 cm in metri cubi, in terametri cubi, in decimetri cubi, in gigametri cubi.
-4
3
-40
3
-1
3
-31
3
[3,50·10 m ; 3,50·10 Tm ; 3,50·10 dm ; 3,50·10 Gm ]
5.La velocità di un corpo vale a 15 cm/s: esprimere tale valore in metri al minuto, in kilometri all'anno, in millimetri
5
all'ora.
[9 m/min; 4730,4 km/anno; 5,4·10 mm/h]
6.Scrivere le seguenti grandezze usando i prefissi SI:
a) 1000000 m;
b) 0,005 g;
c) 35000 s.
7.Scrivere le seguenti grandezze usando i prefissi SI:
a) 54000000 g;
b) 0,000 000 3 m;
c) 1000 W.
[1 Mm; 5 mg; 35 ks;]
[54 Mg; 0,3 μs; 1 kW]
8.Il raggio r di una circonferenza vale (33,8 ± 0,1) dm; calcolare l'area del cerchio di raggio r con l'errore assoluto
2
corrispondente.
[(3600 ± 70) dm ]
9.Trovare l'ordine di grandezza in metri di:
a. l'altezza di un albero
b. l'altezza di un grattacielo di 50 piani
2
c. la distanza Milano-Torino
d. lo spessore di una moneta
e. il diametro di una bottiglia di acqua minerale.
2
5
-3
-1
[10 m; 10 m; 10 m; 10 m; 10 m]
10.
Nelle seguenti espressioni x è misurata in metri, t in secondi, v in metri al secondo,
quadrato. Determinare le unità SI per ciascuna delle seguenti espressioni:
a.
3
v
x
x
; b.
av
-1
-1/2
[s m ; s
c.
2
2
xv
a
d.
x
a
e.
x 2v
a
f.
a in metri al secondo
x2
.
a3
6
; m · s; s ; m s; s ]
11.
La membrana cellulare ha uno spessore di circa 7 nm; quante membrane cellulari occorrono per ottenere una
6
pila alta 1 cm? [1,46 ·10 ]
Cinematica
Rispondere per iscritto ai seguenti quesiti, utilizzando per ciascuno non più di 10 righe:
1.Dare la definizione di sistema di riferimento.
2.Enunciare il principio di inerzia e definire i sistemi di riferimento inerziali.
3.Enunciare il principio di relatività.
4.Dare la definizione di traiettoria e di legge oraria.
5.“Il moto di un punto materiale è uniforme, quindi la traiettoria è rettilinea": discutere la correttezza di tale
affermazione.
6.Ricavare la legge oraria per il moto rettilineo uniforme.
7.Descrivere le caratteristiche del vettore velocità.
8.Descrivere quali informazioni possono essere ricavate dall'analisi di un diagramma orario.
9.Una particella si muove su una retta; rispetto ad un assegnato punto di riferimento essa si trova nel punto di ascissa
+6,0 m all'istante iniziale t0 = 0,0 s, nel punto di ascissa +3,0 m dopo 4,0 s, nel punto di ascissa -2,0 m all'istante t =
12 s. Calcolare la velocità scalare media durante gli intervalli di tempo da 0,0 a 4,0 s, da 4,0 a 12 s e da 0,0 a 12 s.
[-0,75 m/s; -0,63 m/s; -0,66
m/s]
10.
Un ciclista percorre un primo tratto di 1,00 km in 1 minuto e 30,0 s, un secondo tratto di 2,50 km in 2 minuti e
50,0 s, un terzo tratto di 1,30 km in 1 min 40,0 s; calcolare le velocità medie su ciascuno dei tratti e la velocità
media complessiva. La velocità media complessiva si può calcolare come media delle velocità sui singoli tratti?
[11,1 m/s; 14,7 m/s; 13,0 m/s; 13,3 m/s; no]
11.
Due veicoli A e B si muovono uno incontro all'altro di moto rettilineo uniforme con velocità rispettivamente di
45,0 km/h e 54,0 km/h; ad un certo istante il veicolo A passa dal punto X, il veicolo B dal punto Y; se la distanza tra
X e Y vale 247,5 km, calcolare dopo quanto tempo dal passaggio da X e Y i due veicoli si incontrano.
[2 h 30 min]
12.
All'istante t0 = 0,0 s due punti mobili A e B transitano per l'origine O di un sistema di assi cartesiani ortogonali;
A si muove sull'asse x e B sull'asse y. Se le velocità sono rispettivamente 6,0 m/s e 8,0 m/s, calcolare dopo quanto
tempo la distanza tra i due punti vale 73 m.
[7,3 s]
13.
Due ciclisti A e B si muovono di moto uniforme su un percorso rettilineo, nello stesso senso, con velocità
rispettivamente pari a 24 km/h e 32 km/h; quando B passa per il punto O, A ha un vantaggio di 18 km. Calcolare:
a) il tempo che intercorre tra i passaggi di A e B da O;
[45 min]
b) dopo quanto tempo dal passaggio di A da O A sarà raggiunto da B.
[3 h]
14.
Assumendo che la velocità del suono sia pari a 330 m/s, calcolare il tempo necessario ad un aereo che voli al
doppio della velocità del suono per coprire la distanza Milano-Roma, posta uguale a 600 km.
[15,1 min]
15.
Un ragazzo percorre 8m verso Nord e 6m verso Est. Il tempo impiegato nell’intero percorso è 5s. Calcola la
velocità media e la velocità scalare media. Disegna il vettore spostamento e il vettore velocità media
3
16.
I due grafici in figura rappresentano le posizioni in
funzione del tempo di due treni che corrono su due binari
paralleli
Descrivi i due movimenti
I due treni hanno viaggiato con la stessa velocità media?
Esiste un istante, prima di tB in cui i due treni hanno la stessa
velocità?
17.
Due carrellini partono dalle estremità di una rotaia lunga 2m e si muovono l’uno verso l’altro con la velocità di
2m/s e 3 m/s, rispettivamente.
Scegli un sistema di riferimento opportuno
Scrivi la legge oraria di ciascun carrellino e traccia il grafico delle due funzioni
Calcola l’istante e la posizione in cui i due carrelli si incontrano
18.
Un automobilista distratto passa a un semaforo rosso senza fermarsi e procede tranquillamente alla velocità
di 10m/s. Un vigile motorizzato lo insegue, passando dallo stesso semaforo 30s dopo ,alla velocità di 20m/s.
Automobilista e vigile viaggiano a velocità costante. Disegna il diagramma orario di ciascuno dei due moti e
determina dopo quanto tempo e a quale distanza dal semaforo il vigile raggiunge l’automobilista
19.
Alla guida di un’automobile, dopo aver percorso una strada rettilinea per 10 km a 40 km/h, siete rimasti senza
benzina. Avete quindi proseguito a piedi, sempre nella stessa direzione, per 2 km fino al prossimo distributore,
dove siete arrivati dopo 30 minuti di cammino. . Scrivere le equazioni orarie relative a ciascuno dei due percorsi,
tracciare un grafico posizione-tempo dell’intero percorso e calcolare la velocità media
20.
Carlo percorre 6 km a 80 km/h e i successivi 6 km a 120 km/h. Qual è la sua velocità media?
21.
Calcola la velocità media e la
velocità media scalare del moto
descritto dal grafico (s-t) accanto.
Disegna il corrispondente grafico (v-t).
22.
Due treni partono da due stazioni
distanti 20 km dirigendosi uno verso
l’altro rispettivamente alla velocità
costante di v1=50,00 km/h e v2=100,00
km/h. Dopo quanti minuti si
incontrano? dove?
23.
Partendo dal grafico accanto, relativo al
moto di un oggetto P, costruisci il
corrispondente grafico (s-t), sapendo che P si
trova nel punto di ascissa -5m al tempo t=0.
Calcola la velocità media di P nell’intervallo che va
da 4s a 7s.
In quale istante P passa per l’origine? (rispondi sia
guardando il grafico che con calcoli opportuni)
4
24.
Una ruota panoramica di raggio 9,5 m compie un giro ogni 36 secondi. Determinare il modulo e la direzione
dell’accelerazione di un passeggero quando si trova nel punto più alto della ruota e quando si trova nel punto più
basso della ruota.
5
25.
Un satellite artificiale percorre, a quota 5,00 ⋅10 m rispetto alla superficie terrestre, un’orbita circolare con
6
periodo uguale a 94 min e 32 s. Sapendo che il raggio medio della Terra è di 6,38 ⋅ 10 m, quali sono la velocità e
l’accelerazione centripeta del satellite?
3
26.
Un CD del diametro di 13,3 cm, compie 3,00 ⋅ 10 giri al minuto. Quali sono periodo e la velocità angolare del
moto? A quale velocità si muove un punto sul bordo?
27.
Se la ruota di una roulette gira ad una fissata velocità angolare, la relazione che esprime il modulo della
velocità v di un punto della ruota in funzione della distanza dal centro, è una proporzionalità diretta?.
Per apportare gli ultimi ritocchi ad un vaso di terracotta, un vasaio fa compiere alla ruota 7,5 giri. A quanti radianti
equivale questa rotazione?
Forze
1. La figura rappresenta un piano inclinato di lunghezza 100 cm e altezza
incognita x. Una forza F equilibra un corpo di 6,0 kg poggiato su di
esso.
Esprimi come varia l’intensità della forza F necessaria per tenere in equilibrio il
corpo al variare di x e ed esegui un grafico di tale relazione riportando x in
ascisse e F in ordinate
Calcola il valore dell’altezza x del piano se la forza equilibrante è 12 N. Se invece
fosse nota h=100 cm, come varia l’intensità della forza F necessaria per tenere
in equilibrio il corpo al variare della lunghezza x del piano? anche in questo caso
esegui un grafico di tale relazione riportando x in ascisse e F in ordinate.
2. Si consideri il piano inclinato senza attrito. Si sa che
all’equilibrio l’allungamento della molla è 2,0 cm e che
la costante elastica vale 10 N/cm. Calcolare:
a. la forza elastica (disegnala)
b. la componente della forza peso parallela al
piano (disegnala)
c. l’altezza del piano inclinato
3. Descrivere una procedura sperimentale per
determinare la costante di elasticità di una molla.
4. Una chiatta è trainata lungo un fiume tramite due funi agganciate a due autovetture che viaggiano lungo le
rive del fiume; le funi formano un angolo di 45,0° rispetto alla direzione di avanzamento e per fare avanzare la
chiatta è necessaria una forza di 1800 N. Calcolare la forza esercitata su ciascuno dei ganci di traino.
3
[1.27 ·10 kN]
5. Calcolare l'intensità della risultante di due forze applicate ad uno stesso punto, di 7N e 24N rispettivamente,
nei seguenti tre casi:
a. sono parallele ed equiverse b. sono parallele e di verso opposto
c. formano un angolo retto
6. Nella figura a lato sono rappresentate tre forze
che si fanno equilibrio, di cui F1 ha intensità 8N.
Determinare le intensità di F2 e F3.
5
7. Un corpo di massa 10kg appoggiato su un piano orizzontale è applicata una forza di 20N che forma un angolo
di 45° con l'orizzontale. Sapendo che il coefficiente di attrito statico tra corpo e piano vale 0,2:scomponi la
forza in una componente orizzontale ed una verticale e calcolane l'intensità. La forza riesce a mettere in moto
il corpo? Perché?
8. Due individui sostengono un carico di 300N mediante due funi
disposte come in figura a lato. Determinare la forza che deve essere
applicata da ciascuno di essi.
9. Due blocchi di peso P1 e P2 sono appoggiati ai due piani
inclinati rappresentati nella figura in alto a sinistra.
L'intensità di P1 vale 100N. Determinare l'intensità di P2 che,
in assenza di attriti, consente al sistema di rimanere in
equilibrio.
10. Un corpo di massa 10 kg è poggiato su un piano orizzontale. Un secondo corpo è collegato al primo tramite
una corda che passa in una carrucola e scende verticalmente trascinando con sé il primo corpo. Nell'ipotesi in
cui il piano abbia coefficiente di attrito statico pari a 0,4 calcola la massima massa del secondo corpo affinché
il sistema sia in equilibrio.
11. Una molla di costante elastica 20 N/m è poggiata su un piano inclinato di 30° con coefficiente di attrito 0,2. Se
alla molla viene attaccato un corpo di massa 2 kg, determina di quanto si allunga la molla perché il sistema sia
in equilibrio.
6