esp 5

Esperienza n 5: Ponte di Wheatstone, Modulo di Young
1
Esperienza n 5: Ponte di Wheatstone, Modulo di Young
Lo scopo dell'esperienza è di misurare il modulo di Young E di una sbarra 6x6 mm2 di
duralluminio attraverso ad una misura differenziale ottenuta con il ponte di Wheatstone
e facendo uso di trasduttori di tipo estensimetrico.
L'apparato meccanico consiste in una sbarra fissata ad una estremità e sottoposta ad una
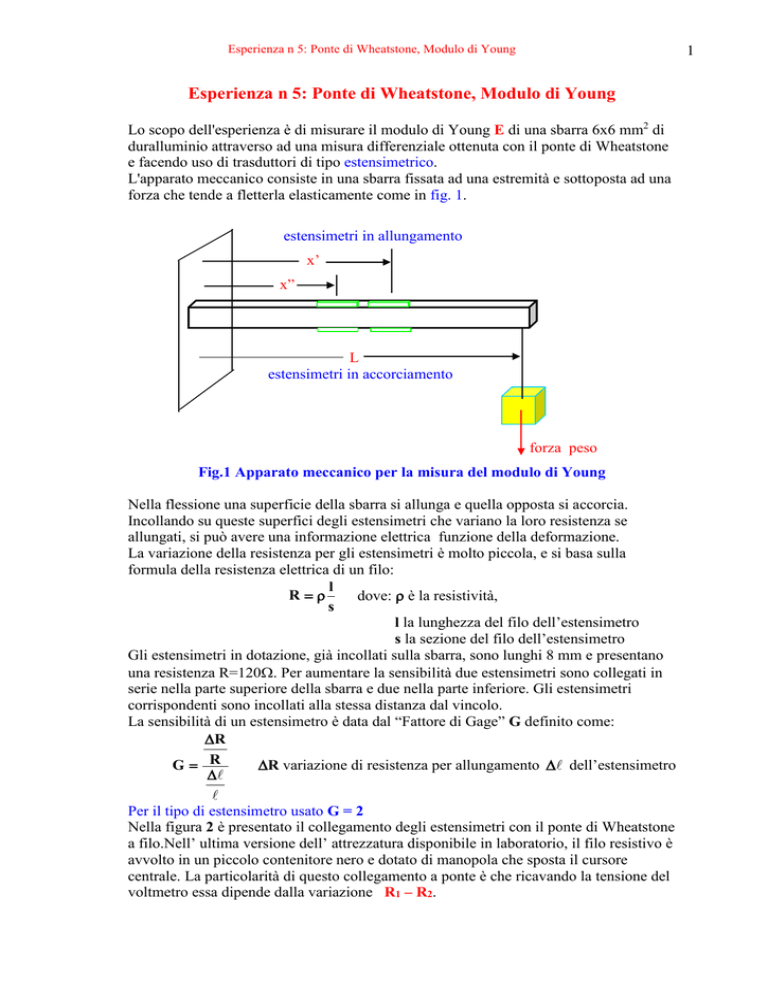
forza che tende a fletterla elasticamente come in fig. 1.
estensimetri in allungamento
x’
x”
L
estensimetri in accorciamento
forza peso
Fig.1 Apparato meccanico per la misura del modulo di Young
Nella flessione una superficie della sbarra si allunga e quella opposta si accorcia.
Incollando su queste superfici degli estensimetri che variano la loro resistenza se
allungati, si può avere una informazione elettrica funzione della deformazione.
La variazione della resistenza per gli estensimetri è molto piccola, e si basa sulla
formula della resistenza elettrica di un filo:
l
R
dove:  è la resistività,
s
l la lunghezza del filo dell’estensimetro
s la sezione del filo dell’estensimetro
Gli estensimetri in dotazione, già incollati sulla sbarra, sono lunghi 8 mm e presentano
una resistenza R=120. Per aumentare la sensibilità due estensimetri sono collegati in
serie nella parte superiore della sbarra e due nella parte inferiore. Gli estensimetri
corrispondenti sono incollati alla stessa distanza dal vincolo.
La sensibilità di un estensimetro è data dal “Fattore di Gage” G definito come:
R
R variazione di resistenza per allungamento  dell’estensimetro
G R


Per il tipo di estensimetro usato G = 2
Nella figura 2 è presentato il collegamento degli estensimetri con il ponte di Wheatstone
a filo.Nell’ ultima versione dell’ attrezzatura disponibile in laboratorio, il filo resistivo è
avvolto in un piccolo contenitore nero e dotato di manopola che sposta il cursore
centrale. La particolarità di questo collegamento a ponte è che ricavando la tensione del
voltmetro essa dipende dalla variazione R1 – R2.
Esperienza n 5: Ponte di Wheatstone, Modulo di Young
B
voltmetro
estensimetri in allungamento
estensimetri in compressione
R1
R2
cursore
A
R1f
D
R2f
C
2V
filo resistivo
V = 2Volt
Fig. 2 Ponte di Wheatstone a filo resistivo, le R1 ed R2 rappresentano gli
estensimetri
Analizzando il circuito si può scrivere:
V
R1
R1  R 2
V
VDA  V2 
R 1f
R 1f  R 2 f
La tensione misurata dal voltmetro inserito nel circuito vale:
 R1

R 1f
V1 – V2 = V 


 R 1  R 2 R 1f  R 2f 
Spostando il cursore D sul filo resistivo si può bilanciare il ponte in modo che:
V1 – V2 = 0
R1
R 1f
da cui ne deriva

R 1  R 2 R 1f  R 2f
Supponendo che gli estensimetri siano ad una temperatura a 25°C e cambiando
semplicemente le notazioni si ha:
R 125C
R 1f

25 C
25 C
R 1f  R 2 f
R1  R 2
Se la temperatura degli estensimetri (essendo gli estensimetri incollati alla sbarra
subiscono tutti lo stesso aumento di temperatura) dovesse cambiare ad esempio arrivare
a 50° si può sostituire il nuovo valore nel bilanciamento considerando che:
R 50C  R 25C (1  t ) con  costante del materiale
VBA  V1 
R 150C
R 125C (1  t )
 25C
C
C
R 150C  R 50
R 1 (1  t )  R 25
(1  t )
2
2
semplificando si deduce che il bilanciamento del ponte rimane inalterato per variazioni
di temperatura degli estensimetri.
Applicando una forza alla sbarra in esame, come in fig. 1, si ottiene un aumento di
resistenza R1 di R1dovuto all'allungamento ed un decremento di R2 di - R2.
2
Esperienza n 5: Ponte di Wheatstone, Modulo di Young
Nel nostro caso R 1  R 1'  R "1 ed R 2  R '2  R "2 perché gli estensimetri sono 2 e
collegati in serie. La variazione di resistenza sarà R 1  R 1'  R "1
La tensione letta diventa:


R 1  R 1
R 1f
V2 - V1 = V 


 R 1  R 1  R 2  R 2 R 1f  R 2f 
Ricordando che gli estensimetri sono uguali e posti alla stessa distanza rispetto al
vincolo si ha:
R1  R 2
 R  R 1

R 1f
V2  V1  V  1


R 1f  R 2f 
 R1  R 2
 R1
R 1
R 1f 
V2  V1  V 



 R 1  R 2 R 1  R 2 R 1f R 2f 
il primo e l'ultimo termine sono uguali se il ponte è bilanciato quindi:
V
V
V2  V1 
R  '
 R 1'  R "1 
"
'
"
R1  R 2
R1  R1  R 2  R 2
Considerato che gli estensimetri sono uguali in lunghezza , ed hanno una resistenza di
120  e sostituendo il valore di Gage:
R 1' ' R '
R "1 " R "
"
e
 ' 








 
  si ha
2R
2R
2R 1'
2R "1
V   '
 " 
V2  V1 
  2R
 2R
=
4R 

 


V
'  "
2
2 V
 '   " 

3)
V
avendo indicato con V la tensione indicata dal voltmetro con  ' l’allungamento
dell’estensimetro corrispondente alla posizione x ' e con  " la posizione
dell'estensimetro corrispondente alla posizione x".
Dalla formula del modulo di Young 2), ricavata in appendice:

6
E
 2 F( L  x 0 )
 ba
si ottiene per i due estensimetri:
 6
'  "   2 F  L  x '   L  x " 
E ba

 12
x '  x" 
'
"

     2 F   L 
E ba
2 

dalla 3) si ottiene:

2 V
 12
x '  x" 
 '   " 
   2 F   L 

V
E ba
2


da cui si può ricavare il modulo di Young:

V
6
V
6
x '  x" 
 
 2 F  L  x 0 
E
 2 F   L 
V ba
2  V ba

con x0 la media della posizione dei due estensimetri.
V 


3
Esperienza n 5: Ponte di Wheatstone, Modulo di Young
-
4
Modo di procedere per la misura:
- Misurare la distanza fra il vicolo e la posizione dove si applica il carico e valutare
l'errore
- Con il tester misurare la resistenza della coppia di estensimetri. Essendo i contatti
degli estensimetri molto delicati, non toccarli con le dita, ma guardarli con una lente di
ingrandimento.
- Montare il circuito elettrico del ponte e spostando il cursore D bilanciare il ponte, in
modo che il voltmetro segni zero.
- Senza toccare il bilanciamento del ponte, cominciare a piegare la sbarra, mettendo un
peso noto (esempio 210  5 gr.)
- costruire il grafico Vvoltmetro = f(Fforza applicata)
Ricavare il "best fit" della retta e ricavare il modulo di Young E con il suo errore.
Estensimetri
L’estensimetro è costituito da un supporto, generalmente plastica, su cui è depositato o
incollato un filo metallico resistivo come schematizzato in fig. 3.
l
filo resistivo
R
Fig. 3 L’estensimetro
Un estensimetro presenta una resistenza R che può dipendere dalla temperatura e perciò
si cerca di applicare questi trasduttori di parametri (da allungamento a cambio di
resistenza) in modo che si possano eseguire misure differenziali come nel nostro caso.
Molto sensibili sono gli estensimetri di semiconduttore.
Allungando un estensimetro si ottiene un allungamento del filo incollato ed una
diminuzione dalla sua sezione quindi un aumento di resistenza R.
Per non danneggiare gli estensimetri l’allungamento possibile è di circa 1% e la sua
resistenza varia quindi di:
R L est

 G F doveGF è il fattore di Gage e nel nostro caso vale 2
R
L est
cioè circa il 2% del suo valore. E’ impensabile quindi effettuare solo misure di
variazione di resistenza con un tester.
Calcolare di quanto si è allungata la superficie superiore ed inferiore della sbarra.