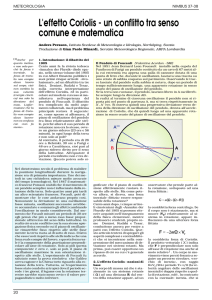
Accelerazione di Coriolis
Corpi in rotazione e forze d'inerzia
Dato un corpo rigido in rotazione attorno ad un asse, tale che, dopo un intervallo di tempo Δt esso
abbia ruotato di un angolo Δθ, si definisce velocità angolare istantanea il limite per Δt → 0 del
rapporto tra la variazione dell'angolo di rotazione (espresso in radianti) e l'intervallo di tempo Δt
(derivata dello spostamento angolare rispetto al tempo)
ω = lim
Δt → 0
Δϑ dϑ
=
Δt
dt
r
Si conviene inoltre di associare a tale grandezza scalare un vettore parallelo all'asse di rotazione
e con il medesimo verso che avrebbe il moto di avanzamento di una vite (destrorsa) che ruoti nello
stesso senso del corpo considerato
r
In tal modo, detto r il vettore distanza che congiunge un punto P del corpo con un punto qualsiasi
r
dell'asse di rotazione, è sempre possibile calcolare la velocità lineare v del punto P come il
prodotto vettoriale
r r r
ω∧r =v
ed in modulo
v = ω ⋅ r ⋅ sen α
dove α è l'angolo (convesso) compreso tra i due vettori, cosicché r sin α è la proiezione di r sulla
retta perpendicolare che congiunge il punto P all'asse di rotazione e rappresenta dunque la distanza
di P dall'asse.
Nel caso della terra è facile verificare che, utilizzando il raggio terrestre, la velocità lineare di un
punto a latitudine ϕ è pari a
v = ω ⋅ r ⋅ sen α = ω ⋅ r ⋅ cos ϕ
Un osservatore solidale con un sistema in moto accelerato, qual è appunto un sistema in rotazione,
non verifica il principio di inerzia (nel senso che sperimenta fenomeni in disaccordo con esso e ne
dimostra quindi la falsità). I sistemi in moto accelerato sono perciò detti sistemi non inerziali. In
essi corpi apparentemente non soggetti a forze manifestano accelerazioni.
In realtà si può dimostrare che la comparsa di tali accelerazioni è legata al particolare sistema di
riferimento considerato ed esse non esisterebbero se il sistema fosse fermo o si muovesse di moto
rettilineo uniforme. Paradossalmente in un sistema accelerato l'inerzia di un corpo si manifesta
come una accelerazione apparente. Per questo motivo tali accelerazioni apparenti vengono attribuite
a forze fittizie dette forze d'inerzia.
La più comune forza d'inerzia è la forza centrifuga che si manifesta in un sistema in rotazione. Un
osservatore solidale con un sistema in rotazione (una giostra ad esempio) si sente spinto verso
l'esterno in direzione normale all'asse di rotazione. Tale sensazione è un effetto dell'inerzia che
tenderebbe a far muovere l'osservatore di moto rettilineo uniforme rispetto al sistema esterno fisso,
lungo la direzione tangente al suo moto rotatorio.
Si può dimostrare che tale forza è proporzionale ad una accelerazione (accelerazione centrifuga)
che vale
r
r r
r
a c = −ω ∧ (ω ∧ r )
E' facile verificare che il prodotto vettoriale è sempre diretto in senso radiale.
Nel caso il corpo si muova di velocità v rispetto al sistema in rotazione compare, oltre alla forza
centrifuga, una seconda forza fittizia, detta forza di Coriolis. Si può dimostrare che tale forza è
proporzionale ad una accelerazione (accelerazione di Coriolis) che vale
r r
r
a Cor = −2ω ∧ v
Tale forza si manifesta ad esempio su tutti i corpi in movimento rispetto alla superficie terrestre,
v v
con l'eccezione dei casi in cui i vettori e v hanno la stessa direzione (in caso di parallelismo
l'angolo compreso tra i vettori e nullo ed essendo sin 0 = 0, anche il prodotto vettoriale si annulla).
Casi del genere si hanno quando un corpo si muove lungo la verticale in corrispondenza dei poli (ad
esempio un grave che cade sopra un polo) o quando un corpo parte dall'equatore con direzione
tangente al meridiano.
Quando un corpo si muove rispetto alla superficie terrestre possiamo distinguere due casi:
a) movimento tangenziale (parallelo alla superficie)
b) movimento radiale (perpendicolare alla superficie)
2
1) Movimento tangenziale
v v
Nel caso di un movimento tangenziale è facile verificare che l'angolo α tra i vettori e v coincide
con l'angolo ϕ di latitudine del corpo
L'accelerazione di Coriolis presenta in tal caso modulo pari a
aCor = 2ω ⋅ v ⋅ sen ϕ
Per la regola del prodotto vettoriale essa è sempre perpendicolare al piano individuato dai due
v v
vettori e v . Il verso è quello di una terna sinistrorsa (poiché il prodotto vettoriale è preceduto dal
segno meno). Il corpo viene quindi deviato verso Est se si muove verso latitudini maggiori (verso i
poli) e verso Ovest se si muove verso le basse latitudini (verso l'equatore).
In pratica ciò comporta una deviazione verso destra nell'emisfero boreale e verso sinistra in quello
australe.
Se il corpo si muove lungo un meridiano (direzione Nord/Sud) l'accelerazione di Coriolis presenta
un'unica componente orizzontale, tangente al parallelo passante per il luogo.
Se il corpo durante il moto cambia la sua longitudine ed il vettore velocità risulta dunque inclinato
rispetto ai meridiani, l'accelerazione di Coriolis presenta anche una componente verticale.
Nel caso la direzione del vettore velocità formi un angolo β con il meridiano passante per il luogo,
possiamo considerare le componenti della velocità lungo il meridiano (v cosβ) e lungo il parallelo
(v sinβ)
La componente lungo il meridiano produce solo una deviazione laterale, mentre la componente
lungo il parallelo produce sia una deviazione laterale che una deviazione verticale.
Per rendercene conto rappresentiamo il moto di un corpo che si muova tangenzialmente ad un
parallelo che non sia l'equatore.
3
Come si può osservare il vettore accelerazione risulta in questo caso perpendicolare all'asse di
rotazione. E' dunque possibile scomporre il suo effetto sul moto del corpo in una componente
tangenziale, che lo devia verso destra, e in una componente verticale (che in questo caso lo devia
verso l'alto).
Naturalmente se il corpo si muove lungo un parallelo in direzione Ovest la componente orizzontale
è diretta sempre verso la sua destra (in questo caso verso il polo nord) mentre la componente
verticale è diretta verso il basso. La componente verticale è tanto maggiore quanto più la direzione
del vettore velocità si scosta dalla direzione del meridiano passante per il luogo e a parità di
inclinazione, diventa via via maggiore scendendo in latitudine. In particolare un corpo che parta
dall'equatore con un qualche angolo rispetto al meridiano presenta solo una componente verticale
che diventa massima quando il suo moto è tangente all'equatore.
In definitiva un corpo che si muova verso est subisce oltre ad una deviazione laterale anche una
deviazione verso l'alto (e pesa quindi meno di un corpo fermo), mentre un corpo che si muova verso
ovest subisce anche una deviazione verso il basso (e peso quindi di più di un corpo fermo).
Possiamo ottenere in modo semplice la relazione di Coriolis per un corpo che si muova
tangenzialmente alla superficie terrestre. Consideriamo il moto di un corpo P che, partendo da un
punto A posto a latitudine ϕ, si sposti con velocità v in direzione sud lungo il meridiano passante
per A. Il punto A si trovi ad una distanza D dall'asse di rotazione e sia quindi animato da una
velocità di rotazione pari a ωD.
Scomponiamo ora la velocità v nella sua componente perpendicolare all'asse di rotazione (v sin ϕ) e
parallela all'asse di rotazione (v cos ϕ).
Dopo un tempo t il corpo si è mosso di un tratto vt lungo la superficie terrestre e si è allontanato
dall'asse di rotazione di un tratto
d = (v sin ϕ) t
Il punto della superficie terrestre posto sullo stesso meridiano (passante per A) alla distanza
dall'asse D + d presenta una velocità di rotazione maggiore del punto A e pari a ω (D + d). Esso
dunque ruota più velocemente rispetto ad A di una quantità
ω (D + d) - ωD = ωd
4
Quando il corpo P giunge dopo un tempo t sopra tale punto lo troverà pertanto spostato verso est di
una quantità
s = t ωd
Esprimendo ora d in funzione della velocità del corpo si ottiene
s = t ω (v sin ϕ) t = ω v t2 sin ϕ
Se dunque interpretiamo tale spostamento come causato da una forza fittizia (di Coriolis) che agisce
in modo costante, possiamo descrivere il movimento in termini di un'accelerazione costante e
confrontare così la relazione precedente con quella del moto uniformemente accelerato
1
s = at 2
2
ed eguagliando i secondi membri troviamo l'espressione dell'accelerazione di Coriolis per un corpo
in moto tangenziale rispetto alla superficie terrestre
a = 2ωv sinϕ
2) Movimento radiale
Nel caso di un movimento radiale (caduta di un grave, proiettile lanciato verticalmente) è facile
v v
verificare che l'angolo α tra i vettori ω e v coincide con la colatitudine, cioè con l'angolo
complementare all'angolo di latitudine.
Se dunque ϕ = 90 - α, l'accelerazione di Coriolis presenta in tal caso modulo pari a
a Cor = 2ω ⋅ v ⋅ sen α = 2ω ⋅ v ⋅ cos ϕ
E' semplice verificare che, per la regola del prodotto vettoriale, l'accelerazione di Coriolis è in
questo caso sempre tangente al parallelo passante per il luogo e orientata verso est.
Calcoliamo ora lo spostamento verso est lungo il parallelo che subisce un corpo in caduta libera da
un'altezza h.
Il tempo t di caduta da un'altezza h di un corpo soggetto all'accelerazione di gravità g è pari a
2h
t=
g
La sua velocità al tempo t (nell'ipotesi che al tempo t = 0 la sua velocità fosse nulla) è pari a
v = gt
Sostituendo l'accelerazione di Coriolis diventa
a Cor = 2ω ⋅ gt ⋅ cos ϕ
Integrando due volte tale relazione si ottiene prima la velocità del corpo verso est
v Cor = ω ⋅ gt 2 ⋅ cos ϕ
5
e infine lo spostamento verso est, dopo un tempo t
1
sCor = ω ⋅ gt 3 ⋅ cos ϕ
3
Sostituendo infine a t il tempo di caduta da un'altezza h si ottiene
2
2h
sCor = ωh
⋅ cos ϕ
3
g
Poiché la terra compie una rotazione completa intorno al proprio asse (2π radianti) in 23h 56m 4s
(giorno sidereo = 86.164 s), la sua velocità angolare è pari a
2π
ω=
= 7,292 ⋅ 10 −5 rad / s
86.164
supponendo di trovarci ad una latitudine di 45° e ad una altezza di 100 m, lo spostamento subito dal
grave sarà
2
2h
2 ⋅ 100
cos α = 7,292 ⋅ 10 −5 ⋅ 100 ⋅
cos 45 = 0,0155 m = 15,5 mm
s = ωh
3
9,8
g
Si ritrova così per via teorica il valore ottenuto sperimentalmente (circa 16 mm) da Guglielmini nel
1691 lasciando cadere dei gravi dalla torre degli Asinelli a Bologna. Si noti che il parallelo che
passa per il luogo non indica la direzione Est-Ovest (quest’ultima è individuata dal cerchio
massimo passante per il luogo perpendicolarmente al meridiano locale). Così il grave, venendo
deviato dalla forza di Coriolis in direzione del parallelo, cade verso Nord-Est (nell’emisfero
boreale).
Il pendolo di Foucault
L'accelerazione di Coriolis è in grado di giustificare anche la rotazione del piano di oscillazione del
pendolo (esperimento di Foucault) a latitudini diverse dall'equatore
Supponiamo che il pendolo si trovi ad una latitudine ϕ e che stia oscillando lungo un meridiano (in
direzione Nord - Sud) muovendosi di un tratto ± r intorno al punto A (si supponga che il filo del
pendolo sia sufficientemente lungo da poter confondere la sua traiettoria curva con un segmento di
retta di lunghezza 2r), raggiungendo alternativamente il punto B e C.
Detta DA la distanza del punto A dall'asse di rotazione sarà allora
6
DC la distanza del punto C dall'asse di rotazione, pari a
DC = D A + d
DB la distanza del punto B dall'asse di rotazione, pari a
DB = D A − d
Le rispettive velocità lineari sono
V A = ωD A
VB = ωDB = ω (D A − d )
VC = ωDC = ω (D A + d )
e la differenza di velocità tra il punto A e gli estremi B e C vale
ΔV = V A − V B / C = ωd
osservando poi che
d = r sin ϕ
la differenza di velocità dei punti estremi rispetto al punto A varrà allora
ΔV = ωr ⋅ sen ϕ
Con tale velocità differenziale rispetto al punto A i punti B e C tracciano intorno ad A Una
circonferenza di raggio r. Ciascun punto completa la sua traiettoria intorno ad A in un tempo t pari a
t=
2πr
2π
86164
.
s
=
=
ωr ⋅ sen ϕ ω ⋅ sen ϕ
sen ϕ
Tale intervallo di tempo è detto giorno pendolare. Esso è pari ad un giorno sidereo ai poli ed
aumenta progressivamente verso l'equatore, dove il suo valore va all'infinito (il piano del pendolo
non ruota).
7