Ingegneria Meccanica <[email protected]> manovellismo.thp
page 1a
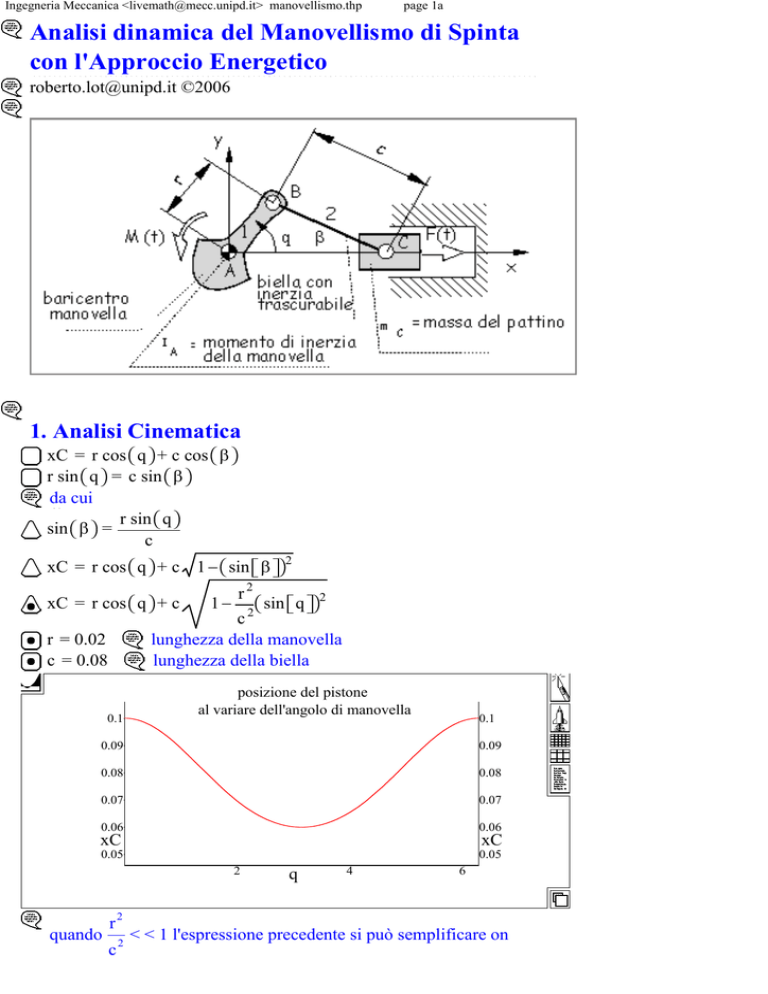
Analisi dinamica del Manovellismo di Spinta
con l'Approccio Energetico
[email protected] ©2006
1. Analisi Cinematica
xC = r cos q + c cos β
r sin q = c sin β
da cui
r sin q
sin β =
c
xC = r cos q + c 1 − sin β
xC = r cos q + c
1−
r2
2
2
sin q
2
c
lunghezza della manovella
lunghezza della biella
r = 0.02
c = 0.08
0.1
posizione del pistone
al variare dell'angolo di manovella
0.1
0.09
0.09
0.08
0.08
0.07
0.07
0.06
0.06
xC
xC
0.05
0.05
2
quando
r
2
c
2
q
4
6
< < 1 l'espressione precedente si può semplificare on
Ingegneria Meccanica <[email protected]> manovellismo.thp
xC S = r cos q + c 1 − 12
r2
2
sin q
page 2a
2
c
l'errore commesso è molto piccolo, come mostrato in figura
approssimazione
dovuta alla formula semplificata
0
0
-1x10-005
-1x10-005
-2x10-005
-2x10-005
-3x10-005
-3x10-005
xC
xC
-4x10-005
-4x10-005
2
q
4
6
2. Analisi dinamica
Inerzia Ridotta
IA = 0.0002
mp = 0.13
inerzia della manovella rispetto al perno di banco A
massa pistone
trascurando l'inerzia della biella, si ottiene
I ' = IA + mp τxC 2
τxC = ∂ xC
∂q
r 2 cos q sin q
τxC = − r sin q −
c 2 − r 2 sin q 2
Ingegneria Meccanica <[email protected]> manovellismo.thp
page 3a
inerzia ridotta
0.000 3
0.000 3
0.000 2
0.000 2
xC
xC
0.000 1
0.000 1
2
q
4
6
Momento Ridotto
M
coppia agente alla manovella
F
forza agente sul pistone
M ' = M + F τxC
coppia ridotta
r 2 cos q sin q
M ' = M + F − r sin q −
− r 2 sin q
2
+ c2
Equazione del moto
2
I ' ∂ ∂ q + 12 ∂ I ' ∂ q = M '
∂t ∂t
∂q
∂t
che ridotto in forma normale diventa
∂ q = q'
∂t
r 2 cos q sin q
−
− r sin q F + M − mp τxC q ' 2 ∂ τxC
2
2
2
∂q
− r sin q + c
∂ q' =
∂t
mp τxC 2 + IA
Moto in assenza di forze esterne
in questo caso l'energia del sistema si conserva
2
To = energiacineticainiziale
∂ q = To
1 IA + mp τxC 2
2
∂t
da cui
To
∂ q=
2
∂t
IA + mp τxC 2
integrando questa equazione differenziale
Ingegneria Meccanica <[email protected]> manovellismo.thp
To = 0.5
page 4a
Tabulate q t with
si ottiene il grafico seguente, che mostra l'irregolarità del moto dovua alle
variazioni di inerzia
irregolarità del moto dovuta
alle variazioni di inerzia ridotta
74
72
70
68
66
64
62
q'
60
0
t
0.02
0.04
0.06
0.08
0.1
Ingegneria Meccanica <[email protected]> manovellismo.thp
page 4b