Quesiti
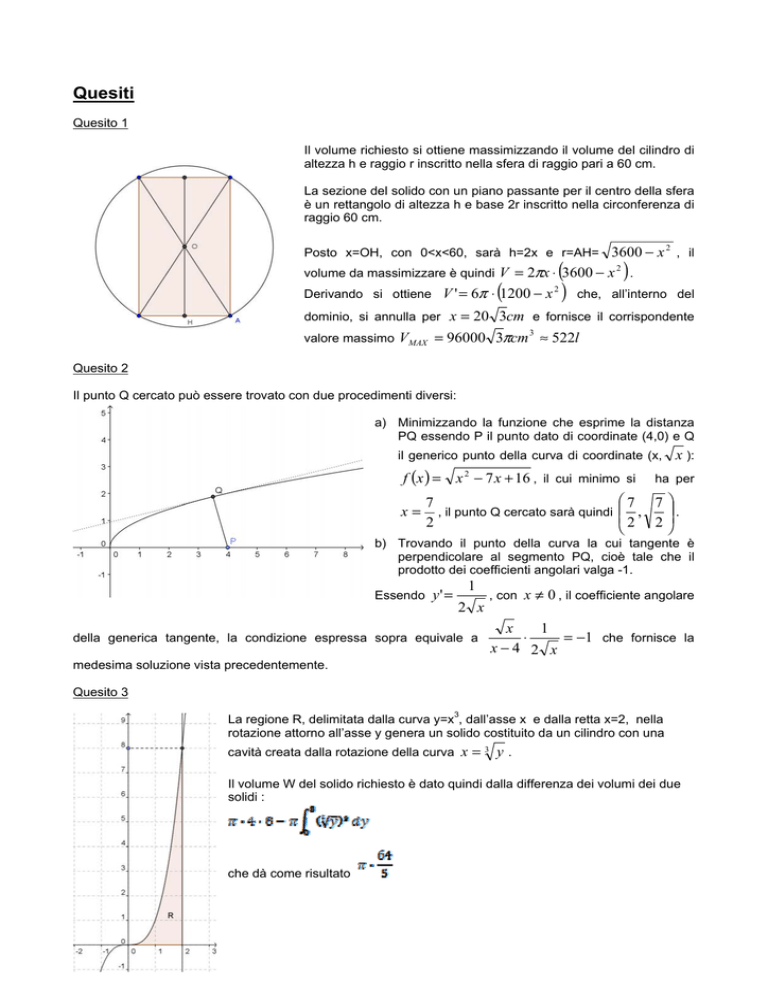
Quesito 1
Il volume richiesto si ottiene massimizzando il volume del cilindro di
altezza h e raggio r inscritto nella sfera di raggio pari a 60 cm.
La sezione del solido con un piano passante per il centro della sfera
è un rettangolo di altezza h e base 2r inscritto nella circonferenza di
raggio 60 cm.
Posto x=OH, con 0<x<60, sarà h=2x e r=AH= 3600 − x , il
2
(
V ' = 6π ⋅ (1200 − x )
volume da massimizzare è quindi V = 2πx ⋅ 3600 − x
Derivando si ottiene
2
2
).
che, all’interno del
dominio, si annulla per x = 20 3cm e fornisce il corrispondente
valore massimo VMAX = 96000 3πcm ≈ 522l
3
Quesito 2
Il punto Q cercato può essere trovato con due procedimenti diversi:
a) Minimizzando la funzione che esprime la distanza
PQ essendo P il punto dato di coordinate (4,0) e Q
il generico punto della curva di coordinate (x,
f (x ) = x 2 − 7 x + 16 , il cui minimo si
x=
7
, il punto Q cercato sarà quindi
2
x ):
ha per
⎛7 7 ⎞
⎜ ,
⎟
⎜2 2⎟.
⎝
⎠
b) Trovando il punto della curva la cui tangente è
perpendicolare al segmento PQ, cioè tale che il
prodotto dei coefficienti angolari valga -1.
Essendo y '=
1
, con x ≠ 0 , il coefficiente angolare
2 x
x
1
⋅
= −1 che fornisce la
x−4 2 x
della generica tangente, la condizione espressa sopra equivale a
medesima soluzione vista precedentemente.
Quesito 3
La regione R, delimitata dalla curva y=x3, dall’asse x e dalla retta x=2, nella
rotazione attorno all’asse y genera un solido costituito da un cilindro con una
cavità creata dalla rotazione della curva x =
3
y.
Il volume W del solido richiesto è dato quindi dalla differenza dei volumi dei due
solidi :
che dà come risultato
Quesito 4
Il numero delle combinazioni di n oggetti a 4 a 4 è dato da
oggetti a 3 a 3 è dato da
, mentre Il numero delle combinazioni di n
.
se k=4 e n-k=3 si trova n=7.
Per la legge delle classi complementari
In alternativa si può applicare le definizione di coefficiente binomiale per cui
all’equazione
che porta
che ha soluzione n=7
Quesito 5
Come risulta chiaro dalla figura, nell’intervallo [1,2] la
funzione y=cos x è non negativa per
negativa per
mentre è
.
Quindi l’area richiesta va calcolata spezzando l’integrale
come segue:
Il risultato sarà dunque uguale a 2 − (sin 1 + sin 2 ) ≈ 0,25
Quesito 6
Il limite, che presenta una forma di indecisione
⎡0⎤
⎢⎣ 0 ⎥⎦ si può risolvere con la sostituzione x-a=y, che lo
trasforma nel limite
e successivamente applicando le formule di addizione per la tangente si ottiene il limite
in cui il primo fattore corrisponde al limite fondamentale che tende a 1, mentre l’altro tende a 1+tg2a e quindi
il limite complessivo è 1+tg2a.
Quesito 7
Consideriamo la funzione f(x)= x2011 + 2011x + 12
f(-1) = - 2000 è un numero negativo mentre f(0)= 12 è un numero positivo, poiché la funzione polinomiale è
continua, per il teorema di esistenza degli zeri esiste, nell’intervallo (-1, 0) almeno un punto in cui f(x)=0.
L’unicità del punto si può dimostrare col calcolo della derivata prima: f’(x)= 2011 x2010+ 2011 questa è
strettamente positiva per qualsiasi x, quindi la funzione è strettamente crescente e la soluzione è unica.
Quesito 8
Il problema della quadratura del cerchio, cioè quello di valutare l’area di un cerchio costruendo un quadrato
ad esso equivalente, compare per la prima volta in un testo egiziano datato attorno al 1650 a.C., detto
Papiro di Rhind, dove lo scriba Ahmes propose una stima del valore della costante π, fissandola uguale a
256 / 81 (circa 3.1605).
Successivamente l'illusione di poter prima o poi esaurire le cifre di π viene infranta da Johann Heinrich
Lambert nel 1761, quando egli dimostra l'irrazionalità di questa costante, cioè l'impossibilità di esprimerla
esattamente attraverso un rapporto di interi come era stato tentato più volte da Ahmes in poi.
Cade infine il sogno greco della quadratura con riga e compasso grazie a Ferdinand von Lindemann, che
dimostra nel 1882 la trascendenza di π, cioè il fatto che questa costante non è soluzione di alcuna
equazione algebrica a coefficienti razionali e non appartiene dunque al campo dei numeri costruibili con riga
e compasso.
Questi reiterati tentativi, distribuiti in oltre tremilacinquecento anni di storia ne hanno fatto il simbolo di tutti i
problemi senza soluzione e ci riportano alla mente i versi del Paradiso di Dante ad esso relativi:
“Qual è 'l geometra che tutto s'affige
per misurar lo cerchio, e non ritrova,
pensando, quel principio ond'elli indige...”
Quesito 9
Consideriamo il triangolo ABC rettangolo in B e il punto M tale che
AM=MC=MB, per le proprietà di inscrivibilità del triangolo rettangolo
nella semicirconferenza di diametro pari all’ipotenusa.
Per dimostrare la tesi richiesta occorre mostrare che:
a) Tutti i punti appartenenti alla retta r passante per M e
perpendicolare al piano del triangolo sono equidistanti dai vertici
A,B,C
b) Solo i punti equidistanti dai vertici A,B,C appartengono alla retta
r.
Dimostrazione:
a) Consideriamo un punto P appartenente ad r e i triangoli PMA,
PMB, PMC: essi sono congruenti per il primo criterio perché
rettangoli con cateti congruenti per ipotesi, quindi sarà
PA=PB=PC
b) Consideriamo ora un punto P tale che PA=PB=PC: il triangolo PAC è quindi isoscele e la sua mediana
PM è anche altezza. I triangoli PMA, PMB, PMC sono quindi congruenti per il terzo criterio ed essendo
PMA e PMC rettangoli per la predetta proprietà dei triangoli isosceli, sarà rettangolo anche PMB, quindi r
è perpendicolare al piano del triangolo ABC.
Quesito 10
La risposta corretta è la D) f(x) =III f ’(x) = II f ‘’(x) = I
Infatti i punti in cui si annulla la derivata prima sono punti a tangente orizzontale di f(x) e gli intervalli di
crescenza e decrescenza corrispondono agli intervalli in cui la derivata prima è positiva o negativa.
Il punto di ascissa 0 è un punto di flesso per la funzione, punto stazionario per la derivata prima e zero per la
derivata seconda.
Gli intervalli in cui la derivata seconda è positiva o negativa corrispondono ai punti in cui la concavità è
rivolta verso l’alto o il basso










