esercizi su circuiti in regime sinusoidale

A. Maffucci: Circuiti in regime sinusoidale
ES. 1.4 ES. 1.1 Esprimere la corrente i(t) in termini di fasore nei seguenti tre casi:
a) i (t ) = 4 sin(ωt − 1.14)
b) i(t) = 10sin(ωt − π)
ver 2 - 2004
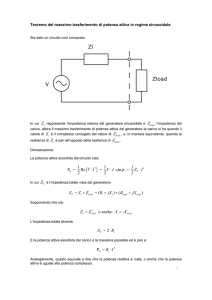
Si consideri il circuito in figura, determinando L tale che la parte immaginaria
dell’impedenza vista ai capi dei morsetti risulti Im{Z& }= 100 Ω.
R
c) i(t) = 8sin(ωt + π / 2)
L
Risultato: a) I = 4 exp(− j1.14) ; b) I = −10 ; c) I = 8 j .
C = 10 µF
C
f = 1 kHz
ES. 1.2 Valutare (in forma cartesiana e polare) le impedenze viste ai capi dei morsetti:
R
2C
R
R
L'impedenza totale vista ai capi dei morsetti è
C
L
ωL
( jωL) /( jωC)
,
Z& = R +
= R+ j
j(ωL −1/ ωC)
1 − ω 2 LC
C
quindi basta imporre
(a )
R = 10 Ω
= 1 mH
L
4
ω = 10 rad / s
Im{Z& } =
(c)
( b)
R = 8 Ω, L = 15 mH
C = 0.4 mF , f = 50 Hz
R = 200 Ω, L = 16 mH
ωL
1 − ω 2 LC
= 100 ⇒
L = 2.19 mH .
C = 10 µF , ω = 2.5 ⋅ 10 3 rad / s
ES. 1.5 - A quale di queste impedenze corrisponde la fase ϕ = −π / 4 ?
Risultato:
c)
a) Z& = 10 + 10 j = 10 2 exp( jπ / 4) Ω ; b) Z& = 8 + 11.54 j = 14 exp( j 0.965) Ω ;
Z& = 8 + 20 j = 21.5 exp( j1.19) Ω ;
ES. 1.3 Le seguenti coppie di fasori esprimono tensione e corrente relative ad un dato
bipolo. Dire, nei tre casi, se si tratta di un resistore, un condensatore o un
induttore e valutare il valore dei parametri corrispondenti R, C o L
a) v(t) = 15cos(400t + 1.2) , i(t) = 3sin(400t + 1.2) ;
b) v(t) = 8cos(900t − π / 3) , i(t) = 2 sin(900t + 2π / 3) ;
c) v(t) = 20 cos(250t + π / 3) , i(t) = 5sin(250t + 5π / 6) ;
& si ha che:
a) V = 15e j1.2 , I = 3e j(1.2−π / 2) . Posto V = ZI
π
arg(Z& ) = arg(V ) − arg(I ) =
2
⇒
Z& = jωL
⇒
j
Z& = −
ωC
ω = 100 rad / s
Caso 3:
⇒
Z& = R
3: R-C parallelo
R = 0.5 Ω
C = 0.2 F
ω = 10 rad / s
4: L-C serie
C =1 F
L =1 H
ω = 1 rad / s
1
1
1
π
Z& = =
=
= 0.25(1 − j) ⇒ ϕ = tg −1 (−1) = − .
4
Y& 1/ R + jωC 2 + 2 j
ES. 1.6 - Dati i seguenti fasori V1 = 10 exp( jπ / 6) , V2 = 10 exp(− jπ / 6) , V3 = 5exp(− jπ / 3) :
⇒
L=
Iω
= 12.5 mH .
⇒
C=
b) calcolare i fasori: V1 + V2 , V1 − V2 , V1 + V3 , V1 − V3 ;
c) rappresentare nel piano complesso i fasori valutati al punto b)
d) rappresentare nel tempo le tensioni corrispondenti ai fasori dei punti a) e b),
I
Vω
= 0.28 mF .
definito la trasformazione fasoriale come segue:
v(t) = V M sin(ωt + α) ↔V = V M exp( jα)
c) V = 20e jπ / 3 , I = 5e j(5π / 6−π / 2) = 5e jπ / 3 . Posto V = Z&I si ha che:
arg(Z& ) = arg(V ) − arg(I ) = 0
2: R-C serie
R = 10 Ω
C = 10 mF
ω = 100 rad / s
a) rappresentare nel piano complesso i fasori V1 , V2 , V3 ;
V
b) V = 8e − jπ / 3 , I = 2e j(2π / 3−π / 2) = 2e − jπ / 6 . Posto V = Z&I si ha che:
π
arg(Z& ) = arg(V ) − arg(I ) = −
2
1: R-L serie
R = 10 Ω
L = 10 mH
⇒
R=
V
I
= 4Ω.
scaricato da www.riccardogalletti.com/appunti_gratis
2
A. Maffucci: Circuiti in regime sinusoidale
ver 2 - 2004
ES. 2.1 - Con riferimento al seguente circuito, valutare l'impedenza Z& eq vista ai capi del
generatore e la potenza complessa S& erogata dal generatore.
R
j (t )
R
j (t ) = 10 sin(2t ) A
R=2Ω
L =1H
C = 0.25 F
L
ver 2 - 2004
ES. 2.3 - Applicando il teorema di Thévenin, valutare la potenza complessa e la potenza
istantanea assorbita dall’induttore L2 .
R
a
i L2 (t )
j (t ) = 10 2 sin(100t + 0.35) A
R = 4 Ω, C = 3 mF,
L2
j (t )
L1
L1 = 2 mH, L2 = 5 mH
b
2. Equivalenza, sovrapposizione degli effetti, potenza.
C
A. Maffucci: Circuiti in regime sinusoidale
Trasformiamo preliminarmente la rete in una rete di impedenze:
J = 10e j 0.35 ,
Z C = −3.33 j,
Z& L1 = 0.2 j,
Z& R = 4, Z& L 2 = 0.5 j
L'impedenza equivalente nel circuito di Thévenin si valuta risolvendo la rete seguente:
Passando al dominio dei fasori si avrà la rete di impedenze:
J = 10,
Z& C = − j /( ωC ) = −2 j,
Z& L = jωL = 2 j,
La tensione a vuoto, invece, si può calcolare a partire dalla
corrente che circola in Z& c , a sua volta ottenuta con un partitore
di corrente:
Z& R = R = 2.
L'impedenza di ingresso vista dal generatore è data da:
Z& eq = Z& R //[ Z& C // Z& R + Z& L ] = 0.8 + j 0.4 Ω.
E 0 = Z& C I C = Z& C J
La potenza complessa erogata da j(t) si valuta facilmente una volta nota Z& eq :
( 1
1 ( 1
(0.8 + j0.4)100
A& J ≡ V J J = Z& eq JJ = Z& eq J 2 =
= 40 + j20 .
2
2
2
2
ES. 2.2 - Con riferimento al seguente circuito, valutare l'impedenza Z& eq vista ai capi del
L
C
+
Z& C
I
V
Z& R
J
Z& L1
E0
Z& C
E0
= −0.089 + j0.570 = 0.577e j1.726 A.
Z& L2 + Z& eq
L’andamento della corrente nel tempo è allora dato da:
generatore e le correnti i L (t) e iC (t)
R
iC (t )
Z& L1
Z& L1
= 0.693 + j1.114 Ω.
&
Z L1 + Z& C + Z& R
Risolvendo la rete equivalente ottenuta, si ha che
I L2 =
i L (t )
Z& R
Z& eq = Z& C //(Z& L1 + Z& R ) = 1.721 − j1.985 Ω.
i L2 (t) = 0.577 2 sin(100t + 1.726) A
e(t)
e(t) = 10 cos(1000t) V
R = 10 Ω L = 20 mH
C = 0.1 mF
La potenza complessa assorbita da L2 sarà puramente reattiva:
A& L2 = jX L2 I 2L = 0.167 j VAr.
2
La potenza istantanea si può valutare, in generale, dalla conoscenza di corrente e tensione:
Risultato: Z& eq = 5 − j15 Ω ; i L (t ) = 0.45 cos(1000t −1.11) A, iC (t) = −sin(1000t) A .
p L2 (t) = v L2 (t)i L2 (t),
ma in questo caso particolare (elemento dinamico) basta la sola conoscenza della i L2 (t) :
pL2 (t) = vL2 (t)iL2 (t) = iL2 (t)
scaricato da www.riccardogalletti.com/appunti_gratis
3
diL2 (t)
dt
=
2
L2 diL2 (t)
= 0.167sin(200t −1.260)W .
2 dt 2
4
A. Maffucci: C ircuiti in regime sinusoidale
ver 2 - 2004
ES. 2.6
ES. 2.4 - Con riferimento al seguente circuito valutare la corrente i L (t ) .
j1 (t) = 10 cos(1000t ) A
R
j1( t )
j 2 (t) = 10sin (1000t ) A
R
C
j2 ( t )
L
i L (t )
A. Maffucci: C ircuiti in regime sinusoidale
ver 2 - 2004
riferimento al seguente circuito valutare la reattanza da inserire in
- Con
parallelo al generatore in modo che l'impedenza complessiva vista dal
generatore stesso assorba la stessa potenza media di prima ma abbia una fase
ϕ tale che cos ϕ = 0.9 ( rifasamento) e la corrente assorbita sia in ritardo
rispetto alla tensione.
L
R=2Ω
L = 2 mH
e(t) +
C = 1 mF
e(t) = 100 sin(ωt) V
R
C
ω = 10 4 rad/s, R = 50 Ω
C = 10 µF,
L
Passando al dominio dei fasori si avrà la rete di impedenze:
J1 = j10 A,
J 2 = 10 A, Z& C = − j Ω,
Passando al dominio dei fasori si avrà la rete di impedenze:
Z& RL = R + jωL = 2 + j2 Ω, Z& R = R = 2 Ω,.
E = 100V , Z& C = −10 j Ω, Z& L = 12 j Ω, Z& R = 50 Ω.
Questa rete può essere risolta con la sovrapposizione degli effetti. Il contributo del solo generatore
J 1 si ottiene dalla rete in cui J 2 è stato sostituito con un circuito aperto:
I L′ = J 1
Z& RC
= 3.33 A , av endo posto
&
Z RC + Z& RL
L'impedenza equivalente vista dal generatore è
Z& C Z& R
Z& eq = Z& L +
= 1.92 + j2.38 Ω,
&
Z C + Z& R
Z& R Z&C
Z& RC =
= 0.4-j 0.8 Ω
&
Z R + Z&C
quindi la potenza complessa erogata dallo stesso sarà
(
1 ( 1 EE 1 E 2
A& = P + jQ = EI = ( = ( = 1.02 kW + j1.27 kVAr .
2
2 Z&
2 Z&
eq
eq
Il contributo del solo generatore J 2 si ottiene dalla rete in cui J 1 è stato sostituit o con un circuito
aperto:
I L′′ = J 2
Z& RC
= − j 3.33 A .
&
Z RC + Z& RL
Il fattore di potenza è pari a
Si ha, quindi
cos ϕ = cos[tg −1 (Q / P)] = 0.63
I L = I L′ + I L′′ = 3.33(1 − j ) = 4.71exp(−0.78 j ) A
quindi occorre inserire un'opportuna Z& x tra l'impedenza Z& eq ed il generatore in modo che
l'impedenza complessiva Z& TOT verifichi tale richiesta. Affinché tale inserzione non alteri la
tensione, Z& x deve essere posta in parallelo al generatore. Per lasciare invariata anche la
potenza media l’impedenza deve essere puramente reattiva:
Z& x = jX .Per stabilire il valore di tale reattanza si può
Z& eq
applicare il principio di conservazione delle potenze, che
Z& x
E +
impone, dopo l'inserzione di Z& x :
a cui corrisponde, nel tempo la corrente
i L (t ) = 4.71sin(1000t − 0.78) A
ES. 2.5 - Applicando il teorema di Norton, valutare la potenza complessa e la potenza
istantanea assorbita dal parallelo R-C in figura.
Pdes = P, Q des = Q + Q x
e(t)
+
L
R
R
C
= 1.2 mH
e(t) = 5 2 sin(1000t + π / 3) V
R = 0.21 Ω,
.
La potenza reattiva Q x si può quindi valutare come segue:
L = 1.12 mH
Q des = Pdes tgϕ des = Ptg[cos −1 (0.9)]
C = 1.23 mF.
⇒
Q x = Ptg [cos −1 (0.9)] − Q = −0.77 kVAr
Imponendo la condizione desiderata su ϕ si ottiene una Q x negativa, il che significa che Z& x è
un'impedenza capacitiva. Ricordando l'espressione della potenza reattiva assorbita da un
condensatore ai capi del quale sia nota la tensione si può valutare il valore di capacità
necessario:
Risultato: A& = 29.72 W − j 7.68 VAr; p(t ) = 29.72 − 30.70 cos(2000t + 2.27)] W .
Q x = −ωC
scaricato da www.riccardogalletti.com/appunti_gratis
5
E2
2
⇒ C =−
Qx
2ωCE 2
= 3.87 µF.
6
A. Maffucci: C ircuiti in regime sinusoidale
ver 2 - 2004
ES. 2.7 - Con riferimento al seguente circuito, calcolare la potenza attiva P2 e la potenza
reattiva Q2 assorbita dalla serie R2 − L2 .
R1
j1( t )
C
L1
A. Maffucci: C ircuiti in regime sinusoidale
ver 2 - 2004
ES. 2.9 - Valutare la corrente che circola nel condensatore e la potenza complessa da
o assorbita.
ess
j1 (t) = 4 cos(4t ) A
j 2 (t) = 2 cos(4t − 2π / 3) A
R2
j2 ( t )
L2
R
R1 = R2 = 2 Ω
+
e(t)
i (t )
j(t) = 2 2 sin(2πft + 0.12) A,
L
C
j(t)
R
L1 = L2 = 1 H
e(t) = 10 2 cos(2πft) V , f = 50 Hz
R = 1 Ω, C = 1 mF, L = 3 mH
C=2F
Risultato: i(t) = 3.15sin(2πft + 0.23) A; A& = -j15.80 VAr .
Passando al dominio dei fasori si avrà la rete di impedenze:
J 1 = 4, J 2 = 2e − j 2π / 3 , Z& C = − j / 8 Ω, Z&1 = Z& 2 = 2 + 4 j Ω.
Applicando la sovrapposizione degli effetti, valutiamo il contributi dovuti a J 1 ed a J 2
ES . 2.10 - Valutare la potenza istantanea e complessa assorbita da R.
R
Z&1
I 2′ = J 1
= 2.03 + j0.01 A,
&
Z C + Z& 2 + Z&1
I 2′′ = J 2
Z&1 + Z& C
= −0.50 − j0.85 A.
&
Z C + Z& 2 + Z&1
j1 (t) = 2 sin(2πft) A,
j1 (t ) C
L
j2 (t) = 2 2 sin(2πft + π / 4) A, f = 50 Hz
j 2 (t )
R = 1.3 Ω, C = 2.0 mF, L = 1.1 mH
Pertanto si ha
I 2 = I 2′ + I 2′′ = 1.53 − j0.84 = 1.75exp(− j0.502) A,
Risultato: p(t) = 4.74[1 − sin(4πft + 6.10) W; A& = 4.74 W .
quindi la potenza complessa assorbita da Z& 2 sa rà
1 (
1
2+4j
A& = P2 + jQ2 = V2 I 2 = Z& 2 I 22 =
1.75 2 = 3.06 W + j7.12 VAr .
2
2
2
Nota: si svolga l’esercizio utilizzando l’equivalente di Thévenin ai capi della serie considerata.
ES. 2.11 - Con riferimento alla seguente rete in regime sinusoidale, valutare:
a) il circ uito equivalente di Thévenin ai capi di R2
b) la corrente circolante in R2
ES. 2.8 - Applicando il teorema di Thévenin, valutare la potenza complessa e la potenza
istantanea assorbita dal condensatore C .
c) la potenza istantanea e complessa assorbita da R2 .
L
R1
a
j(t)
R1
e(t)
R1 = 12 Ω R2 = 2 Ω
R2
C
i
j(t) = 2 2 cos(20t + 0.23) A
L = 0.2 H
+
j(t)
C = 0.1 F
L
C
e(t) = 10 2 sin(ωt + π / 3) V ,
R2
j(t) = 2 sin(ωt + π / 4) A, ω = 103 rad / s
b
C = 4.1 mF, L = 3.2 mH
R1 = 1.2 Ω, R2 = 3.3 Ω,
a) Z& eq = 0.05 + j2.97Ω; E0 = 2.09 − i0.76 V
Ris
Risultato: A& = − j0.49 VAr; p(t) = -0.49 cos(2000t − 3.12)] W .
ultato:
b) i(t) = 0.71sin(1000t −1.08) A
c) A& = 0.82 W ; p(t) = 0.82[1 − sin(2000t − 2.15)] W
scaricato da www.riccardogalletti.com/appunti_gratis
7
8
A. Maffucci: C ircuiti in regime sinusoidale
ver 2 - 2004
A. Maffucci: C ircuiti in regime sinusoidale
3. Doppi-bipoli, generatori pilotati, regime periodico.
I ′ = J1
ES. 3.1 - Con riferimento al seguente circuito, valutare:
i1 (t)
e1 (t )
C
R
Z& C′′
= e j 3.12
&
Z C′′ + Z& L′′ + Z& R′′
⇒
i ′′(t ) = sin(200t + 3.12) A.
Nota la corrente si può calcolare la potenza istantanea assorbita da R e quindi la potenza media:
e1 (t) = 10 cos(1000t) V
+
i ′(t ) = cos(100t + 3.13) mA.
i (t ) = i ′(t ) + i ′′(t ) = 10 −3 cos(100t + 3.13) + sin(200t + 3.12) A.
L
R
⇒
Quindi la corrente che circola in R sarà
i2 (t)
+
Z& L′
= 10 −3 e j 3.13
Z& L′ + Z& C′ + Z& R′
I ′′ = − J 2
a) la matrice delle ammettenze Y& del doppio-bipolo visto ai capi dei generatori;
b) la potenza complessa A& erogata dai generatori;
ver 2 - 2004
T
e2 (t) = 20sin(1000t) V
e2 (t)
R = 1 Ω L = 1 mH
P=
C = 1 mF
T
T
T
T
1
1
2R
R
R
p (t )dt = ∫ Ri 2 (t )dt = ∫ i ′ 2 (t )dt + ∫ i ′′ 2 (t )dt +
i ′(t )i ′′(t )dt
T ∫0
T0
T 0
T 0
T ∫0
 2π 2π 

T = max ,
 ω1 ω 2 
I primi due contributi rappresentano le potenze medie dissipate nei circuiti I e II, quindi sono:
a) Y&11 = 0.5 Ω −1 , Y&m = 0.5 j Ω −1 , Y&22 = 0.5 − j Ω −1 ;
b) A&1er = 75W , A& 2er = 50W + j200VAr .
Risultato:
T
ES. 3.2 -Con riferimento al seguente circuito, valutare la potenza media P assorbita dal
resistore R e verificare che è possibile sovrapporre le potenze medie.
R
i
j1 (t) = cos(100t) A
j1 (t )
R
R
i ′′ 2 (t)dt = I ′′ = 0.5 W
T ∫0
2
.
L'ultimo contributo è nullo perché per ω1 ≠ ω 2 si ha:
T
∫ cos(ω1t + α)sin(ω2t + β)dt = 0
0
∀α,β
.
In definitiva se ω1 ≠ ω 2 è possibile sovrapporre le potenze medie: P ≈ 0.5 W .
j 2 (t) = sin(200t) A
j 2 (t)
C
L
T
R 2
R
i′ (t)dt = I ′ = 0.5 ⋅10 −6 W ,
T ∫0
2
R = 1 Ω L = 1 mH
ES. 3.3 -C on riferimento al seguente circuito, valutare la corrente i(t).
C = 0.1 mF
i(t)
E
+
j(t) = J m cosωt
L
R
Poiché i generatori non sono isofrequenziali, cioè ω1 ≠ ω 2 , il circuito non ammette un regime
sinusoidale ma un regime periodico e quindi non è possibile trasformare la rete in una rete di
impedenze. Tuttavia, essendo la rete lineare, si può applicare la sovrapposizione degli effetti e
ricavare la corrente che circola in R come i = i ′ + i ′′ , dove i ′ si ricava dal circuito ausiliario I e
i ′′ dal circuito ausiliario II.
R
R
i′
C
R
j(t)
J m = 1 A, ω = 10 6 rad / s
E = 1V
R = 1Ω, L = 1mH , C = 1mF
La corrente i(t ) si può calcolare con la sovrapposizione degli effetti nel dominio del tempo:
i (t ) = i1 + i 2 (t ) .
L
C
L
j 2 (t )
C
Il contributo i1 è dovuto al solo generatore di tensione e si ottiene tenendo conto che, in regime
stazionario, l'induttore si riduce ad un corto-circuito ed il condensatore ad un circuito aperto:
i1 = E / 2R = 1/ 2 A .
I
Il contributo i 2 (t )
è
sinusoidale:
Ciascuna di queste due reti può essere rappresentata da una rete di impedenze:
rete I:
J 1 = 1,
rete II:
J 2 = 1,
Z& C′ = −100 j,
Z& ′′ = −50 j,
C
Z& L′ = 0.1 j,
Z& L′′ = 0.2 j,
Z& R′ = 1.
Z& R′′ = 1.
dovuto al solo generatore j(t) e si ottiene risolvendo la rete in regime
J = 1 , Z& R = 1 , Z& C = − j10 −3 , Z& L = j10 3 .
Posto Z& a = Z& R // Z& C + Z& L , la corrente I 2 si ottiene con un semplice partitore di corrente:
Applicando i partitori di corrente:
I 2 = −J
Z& R
≈ −10 −6 + j10 −3 ≈ j10 −3 = 10 −3 e jπ / 2
Z& R + Z& a
⇒ i 2 (t) = −10 −3 sin(ωt) A.
scaricato da www.riccardogalletti.com/appunti_gratis
9
10
A. Maffucci: C ircuiti in regime sinusoidale
ver 2 - 2004
ES. 3.4 -Con riferimento al seguente circuito, valutare la potenza media P assorbita dal
resistore R2 e verificare che è possibile sovrapporre le potenze medie.
j (t )
e(t)
R1
L = 0.2 H
L
v S (t)
+
Ro
C
vin
C = 10 mF
v S (t) = 10 cos(ωt) V
L
RU
gvin (t )
Ri
−
Risultato: P = 0.41 kW .
ver 2 - 2004
ES. 3.6 - Il circu ito seguente riproduce lo schema equivalente di un amplificatore a
transistor per alta frequenza. Determinare la tensione ai capi del resistore RU.
RS +
R1 = 12 Ω R2 = 2 Ω
R2
C
C
j(t) = 14 A
e(t) = 110 cos(20t) V
+
A. Maffucci: C ircuiti in regime sinusoidale
+
ω = 10 8 rad / s
vU
R S = Ro = 1Ω, Ri = 5 Ω
−
L = 1 pH C = 1 nF
g = 100 Ω −1
Risultato: vU (t) = 95.9 cos(ωt + 3.06)
.
ES. 3.5 -Valutare l'equivalente di Thévenin ai capi dei morsetti 1-1'.
i(t)
ES. 3.7 - Con riferimento al seguente circuito valutare la corrente i1 (t) nel circuito
1
e(t) = 2sin(ωt + π / 6) V
R =2Ω r =3Ω
C
e(t)
+
+
R
ri(t)
XL = 4Ω
primario.
i1 (t)
XC =1Ω
1′
kV
+
e(t)
e(t) = 10 2sin(1000t) V
R1
L2
L1
R1 = 1 Ω R2 = 200 Ω
R2
L1 = 3 mH
E = 2e jπ / 6 ,
Z& C = − j ,
Z& L = 4 j ,
Z& R = 2.
Per calcolare V0 basta applicare la LKT alla maglia di sinistra della rete
E = Z& L I + rI
⇒
I =
Poiché L1 L2 ≠ M 2 l' accoppiamento non è perfetto.
Posto L1 = L1′ + L1′′ , possiamo scegliere L1′′ in modo che l'aliquota L1′′ verifichi le condizioni di
E
= 0.368 − j 0.157
Z& L + r
.
′ 2 = M 2:
accoppiamento perfetto L1′L
Applicando un partitore di tensione si ha, quindi:
V0 = rI
L2 = 200 mH
M = 20 mH
Passando alla rete di impedenze si avrà:
L1′′L2 = M 2
Z& R
= 1.070 + j0.064 = 1.07e j0.06 V .
Z& R + Z& C
⇒
L1′′ = M 2 / L2 = 2 mH .
A questo punto il circuito equivalente sarà il seguente
Per calcolare Z& eq occorre spegnere tutti (e soli) i generatori indipendenti, cioè E . Applicando
ancora la la LKT alla maglia di sinistra della rete:
0 = Z& L I + rI
⇒
I =0
e(t)
quindi nella rete per il calcolo di Z& eq risulta spento anche il generatore controllato, visto che la
sua variabile di controllo è nulla, per cui in definitiva:
Z& R Z& C
Z& eq =
= 0.4(1 − 2 j) Ω
&
Z R + Z& C
L1′
i1 (t )
+
R1
a
L1′′
R2
a=
L1′′
= 0.1
M
Per la formula del trasporto dell'impedenza in un trasformatore ideale, il circuito è anche
equivalente al seguente:
scaricato da www.riccardogalletti.com/appunti_gratis
11
12
A. Maffucci: C ircuiti in regime sinusoidale
ver 2 - 2004
L1′
i1 (t)
e(t )
+
R1
a 2 R2
Trasformato il circuito in una rete di impedenze, nella quale si è introdotto il fasore E = 10 V ,
l'impedenza equivalente vista dal generatore è:
a 2 R jωL1′′
= 2+2j Ω
Z& eq = R1 + jωL1′ + 2 2
a R2 + jωL ′′
da cui
I1 =
E
5
5 − jπ / 4
= (1 − j) =
e
A
Z& eq 2
2
⇒
i1 (t) = 5sin(1000t − π / 4) A .
ES. 3.8 - Con riferimento al seguente circuito valutare la potenza complessa assorbita dal
condensatore.
R2
j(t)
L1
R1
L2
C
j(t) = 10 2 cos(100t) A
R1 = R2 = 5 Ω
L1 = 1 mH ,
L2 = 4 mH
M = 2 mH , C = 12.5 mF
Risultato: A& = − j5
.
VAr
scaricato da www.riccardogalletti.com/appunti_gratis
13