Misure di campi magnetici:
bobine di Helmholtz e solenoidi
———- S.S., 12 Settembre 2007 ———Per il calcolo del campo magnetico prodotto da una corrente che fluisce in un
circuito di forma nota è utile servirsi di una relazione matematica nota come prima
formula di Laplace:
~ =
dB
µ0 d~l ∧ ~r
i
4π r 3
(1)
~ prodotto da un elemento
Si tratta di una relazione vettoriale che fornisce il campo B
di circuito d~l, percorso da una corrente i, in un generico punto P posto a distanza ~r da
d~l. La prima formula di Laplace non è una legge fisica, in quanto non consiste in una
relazione fra grandezze misurabili (in nessun procedimento di misura è possibile separare il contributo al campo dovuto al tratto infinitesimo di circuito d~l); è tuttavia una
relazione utile per calcolare, mediante operazione di integrazione, il campo prodotto
dalla corrente che scorre in un tratto finito di circuito.
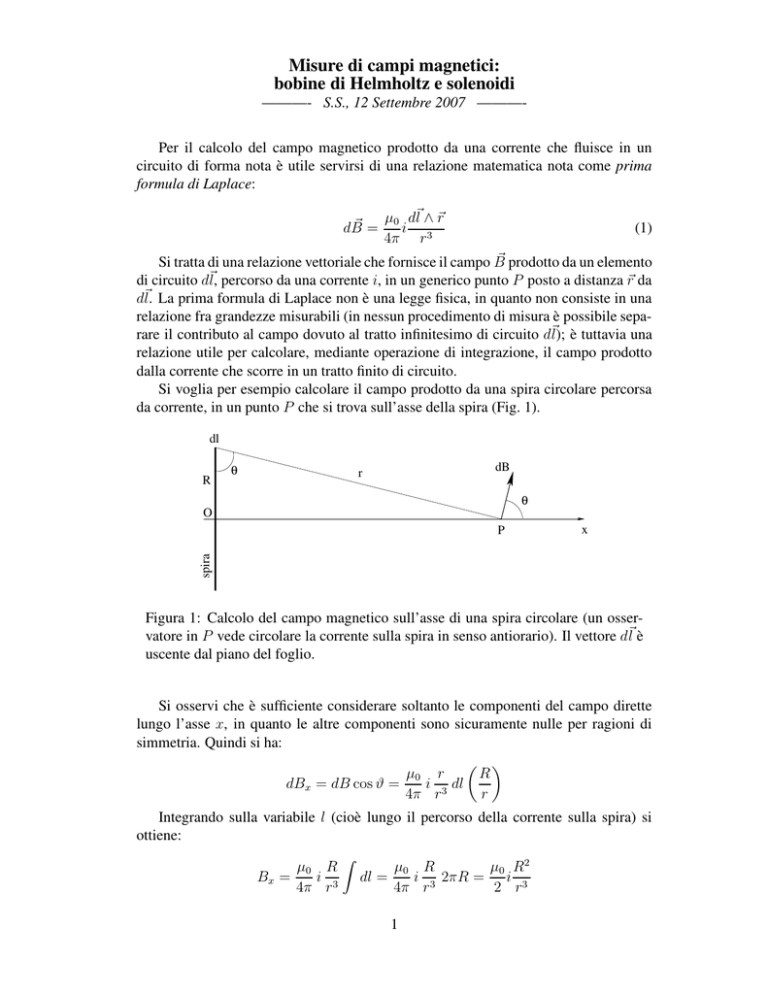
Si voglia per esempio calcolare il campo prodotto da una spira circolare percorsa
da corrente, in un punto P che si trova sull’asse della spira (Fig. 1).
dl
R
θ
dB
r
θ
O
x
spira
P
Figura 1: Calcolo del campo magnetico sull’asse di una spira circolare (un osservatore in P vede circolare la corrente sulla spira in senso antiorario). Il vettore d~l è
uscente dal piano del foglio.
Si osservi che è sufficiente considerare soltanto le componenti del campo dirette
lungo l’asse x, in quanto le altre componenti sono sicuramente nulle per ragioni di
simmetria. Quindi si ha:
µ0 r
R
dBx = dB cos ϑ =
i 3 dl
4π r
r
Integrando sulla variabile l (cioè lungo il percorso della corrente sulla spira) si
ottiene:
Z
µ0 R
µ0 R 2
µ0 R
i 3 dl =
i 3 2πR = i 3
Bx =
4π r
4π r
2 r
1
Poiché r =
√
R2 + x2 , si può scrivere:
Bx =
R2
µ0
i
2 (R2 + x2 ) 32
(2)
L’eq. 2 può essere utilizzata per il calcolo di campi magnetici prodotti da circuiti
di forma più complessa, come le bobine di Helmholtz o il solenoide. Le bobine di
Helmholtz sono una coppia di bobine con alcune caratteristiche particolari (Fig. 2):
• hanno entrambe raggio R;
• hanno una lunghezza L molto più piccola del raggio R;
• sono disposte, a distanza R, in modo che gli assi di simmetria delle due bobine
siano coincidenti;
• hanno lo stesso numero N di avvolgimenti;
• sono elettricamente collegate in serie, in modo che il verso di percorrenza delle
due correnti sia lo stesso.
R
R
C
x
C
L
Vista frontale
Vista laterale
Figura 2: Schema di una coppia di bobine di Helmholtz
Vogliamo calcolare il campo prodotto da tali bobine nel punto C. Iniziamo con il
calcolo del campo prodotto da una sola bobina in un punto generico P sull’asse. Si può
utilizzare l’eq. 2, visto che ciascuna bobina non è altro che la sovrapposizione di N
spire, tutte poste a distanza ~r dal punto P . Il campo risultante sarà dato semplicemente
da:
Bx =
µ0
R2
iN
3
2
(R2 + x2 ) 2
Valutando il campo nel punto C (che ha ascissa x = R/2) e considerando anche il
contributo (identico) della seconda bobina, si ha:
32
µ0 i N
4
Bx = µ 0 i N 3 =
5
R
R2 2
R2 +
4
R2
2
(3)
Il campo magnetico prodotto da una coppia di bobine di Helmholtz è piuttosto
uniforme, in un piano perpendicolare all’asse delle bobine e passante per il punto C
di Fig. 2. Nella Fig. 3 è riportato con linea rossa l’andamento atteso del campo in
funzione del raggio, proprio su tale piano. Il cerchio tratteggiato delimita la zona in
cui la variazione del campo generato è inferiore al 3% rispetto al campo massimo
(quello nel punto C). Le bobine di Helmholtz vengono spesso utilizzate in situazioni
in cui c’è bisogno di un campo uniforme in una zona estesa.
B / BC
1
0.9
0.8
0.7
0.6
0.5
0.4
0.3
0.2
0.1
0
1 r/R
Figura 3: Campo prodotto dalle bobine di Helmholtz in direzione assiale (cioè lungo
l’asse x mostrato in Fig. 2) in funzione della posizione lungo il raggio, nel piano
passante per il punto C e perpendicolare all’asse x.
Con considerazioni analoghe a quelle utilizzate nel calcolo che ha portato al risultato contenuto nell’eq. 3, è possibile determinare il campo magnetico prodotto in un
punto P sull’asse di un solenoide (Fig. 4) di lunghezza L e raggio R ∗ .
Il calcolo che segue è basato sull’assunzione che l’avvolgimento del solenoide sia sufficientemente
“compatto”, cioè che la distanza fra due spire contigue sia molto minore del raggio del solenoide e non
maggiore delle dimensioni della sonda con cui si misura il campo.
∗
3
du
0
θ
u
P
R
u
uP
L
Figura 4: Schema di un solenoide di lunghezza L e raggio R.
Se le spire del solenoide sono avvolte con passo costante, grazie all’eq. 1 si può
calcolare il contributo al campo magnetico dovuto alle dN spire contenute nel tratto
du (dN = N du/L, se N è il numero totale di avvolgimenti). Infatti, osservando che
x = uP − u ( x è la distanza fra la spira che produce il campo e il punto in cui il campo
deve essere calcolato), si può riscrivere il contributo al campo della fettina di larghezza
du utilizzando l’eq. 2:
dBx =
R2
µ0 N
i du
3
2 L
(R2 + (uP − u)2 ) 2
Osservando poi che R/(uP − u) = tan ϑ e dunque uP − u = R/ tan ϑ, si può
scrivere:
R
1
R
du
=
=
2
2
dϑ
tan ϑ cos ϑ
sin2 ϑ
Sostituendo il differenziale du nella relazione precedente per dBx e notando che
R2 + (uP − u)2 = R2 / sin2 ϑ si ottiene:
µ0 N
µ0 N
R2
R
dBx =
dϑ =
i
i
sin ϑ dϑ
3
2
2 L
2 L
sin ϑ
2
R2
sin2 ϑ
Per ottenere il campo prodotto da tutti gli avvolgimenti del solenoide, è ora sufficiente integrare sulla variabile ϑ, nell’intervallo angolare compreso fra ϑ 1 e ϑ2 (Fig. 5).
Il risultato è questo:
µ0 N
i
Bx =
2 L
Z
ϑ2
sin ϑ dϑ =
ϑ1
µ0 N
i
(cos ϑ1 − cos ϑ2 )
2 L
(4)
Nel caso in cui il solenoide sia “indefinito” (cioè se L R) per tutti i punti
P sull’asse del solenoide, purché non troppo vicini ai bordi, i due angoli ϑ 1 e ϑ2
hanno valori non molto diversi da 0 e π rispettivamente, e il loro coseno può essere
ragionevolmente approssimato con ±1. In questo caso la formula si semplifica, come
è noto, e il valore del campo risulta uniforme lungo l’asse con valore:
Bx = µ 0 i
4
N
L
(5)
θ2
θ1
P
R
L
Figura 5: Individuazione degli “angoli–limite” per un punto P sull’asse di un
solenoide di lunghezza finita.
In Fig. 6 è riportato, in funzione della posizione lungo l’asse, il rapporto fra i valori
del campo forniti dalle eq. 4 e 5 per quattro solenoidi, con uguale lunghezza e raggio
sensibilmente diverso. È molto istruttivo osservare quale rilevanza hanno in ciascun
caso gli effetti di bordo, e, di conseguenza, anche il valore del campo nel centro. Infatti,
se la sonda di un teslametro viene posta al centro di un solenoide, il campo misurato
risulterà pari a:
N
N
Bx = µ 0 i
cos ϑ ' µ0 i
se L R
L
L
dato che cos ϑ2 = − cos ϑ1 nel caso in cui P è al centro del solenoide. Si noti che in
questo caso l’angolo ϑ si può ricavare in modo semplice dalla relazione tan ϑ = 2R/L.
Per mezzo del teorema della circuitazione è possibile trovare un’altra proprietà
caratteristica di un solenoide indefinito: il campo all’interno è uniforme, cioè assume
in qualsiasi punto il valore che ha sull’asse.
Misure in laboratorio Le misure di campi magnetici si basano solitamente su teslametri corredati di sonde a effetto Hall. Il funzionamento di tali sonde può essere
illustrato facendo ricorso allo schema della Fig. 7. Una sonda di Hall è sostanzialmente una placchetta di materiale semiconduttore dotata di quattro terminali. Due
terminali, A e B, su lati opposti della placchetta, servono a farvi circolare una corrente
costante i, mediante un generatore di tensione continua con buone caratteristiche di
stabilità. Se la placchetta si trova in una regione in cui è presente un campo magnetico, sui portatori di carica che la attraversano (elettroni che si muovono da B ad A)
agisce la forza di Lorentz, che produce una deriva delle cariche libere in direzione ortogonale sia al campo magnetico che alla direzione individuata dal segmento AB. Se,
come in figura, il campo magnetico è entrante nel piano del foglio, si ha come effetto
un accumulo di carica negativa sulla parte superiore del rettangolo rispetto alla pagina
(e un conseguente accumulo di carica positiva sulla parte inferiore). Si crea pertanto
un campo elettrico fra questi due lati, proporzionale all’intensità del campo magnetico
nella direzione ortogonale al piano della placchetta, che tende a ristabilire la neutralità
delle due zone. Se con un voltmetro opportunamente sensibile si misura la differenza
5
Figura 6: Andamento del campo sull’asse di un solenoide, per alcuni valori del
rapporto L/R.
B
D
−−−−
B
A
++++
i
C
+−
Figura 7: Schema di una sonda di Hall.
6
sonda assiale
B
sonda tangenziale
B
Figura 8: Direzione del campo misurato nelle sonde di Hall assiale e tangenziale.
di potenziale VCD è possibile risalire da questa al valore del campo magnetico che la
produce, dopo aver calibrato la sonda con campi d’intensità nota † .
In genere le sonde hanno un supporto di forma allungata, ad asticella, per consentirne l’inserimento anche in piccole cavità. Le sonde a effetto Hall forniscono l’intensità
del campo in una direzione fissata e, pertanto, esistono sonde assiali e sonde tangenziali a seconda della direzione del campo che si vuole misurare (Fig. 8); infatti, come
abbiamo detto, le possibilità di orientamento della sonda nello spazio sono talvolta
limitate dalla configurazione geometrica del sistema.
Nelle nostre esercitazioni in laboratorio si usa una sonda assiale. Nella prima misura si esegue una mappatura radiale del campo prodotto dalle bobine di Helmholtz ‡ ,
e ci si aspetta di ottenere un andamento simile a quello riportato in Fig. 3. A questo
scopo ci si sposta, tenendo la sonda parallela all’asse di simmetria delle bobine, sul
piano mediano delle bobine e su piani paralleli a questo (per esempio a x = ±3 cm e
a x = ±6 cm). I valori ottenuti vanno riportati in grafico in funzione della coordinata
r. È anche possibile eseguire una mappatura del campo sull’asse delle bobine.
Nella seconda misura si determina il numero di avvolgimenti di un solenoide facendovi passare una corrente d’intensità nota § e misurando il campo magnetico prodotto
all’interno. Per ottenere un risultato accurato è conveniente ripetere la misura per diversi valori della corrente, eseguendo poi una interpolazione lineare dei valori di corrente
e campo magnetico per determinare il numero incognito di spire. Stimare l’incertezza
nella misura e valutare se il solenoide assegnato può essere considerato indefinito o se,
invece, è necessario ricorrere alla formula valida nel caso generale, descritta dall’eq. 4.
Se la corrente nei conduttori fosse trasportata da portatori con carica positiva anziché da elettroni,
si accumulerebbero anch’essi nella parte superiore della placchetta. Per questo motivo, il segno della
differenza di potenziale VCD ci dice in modo univoco qual è la carica dei portatori, ed è stato dimostrato
che si tratta di particelle con carica negativa.
‡
Le bobine di Helmholtz del laboratorio hanno N = 130 spire e raggio R = 15 cm.
§
Quando si fa passare una corrente piuttosto elevata (i ? 2 A) nelle bobine di Helmholtz e nel
solenoide è opportuno controllare che non ci sia un surriscaldamento del filo dovuto all’effetto Joule!
†
7












