I.T.C.G.CARLOCATTANEO–viaG.Impastaton.3,Castelnovone’Monti(ReggioEmilia)
Appunti
L’ACCELERAZIONEDIGRAVITA’ELACADUTADEIGRAVI
CorsodiFisicaeLaboratorio–prof.MassimoManvilli
SEZIONEITI–ITCGCattaneo-Castelnovone’Monti(RE)
---------------------------------------------------------------------------------------------------------------------------------
NEWTON E LA GRAVITA’
Come sappiamo Isaac Newton , basandosi sulle note leggi di Keplero, determinò la famosa formula che
descrive il funzionamento delle forze gravitazionali :
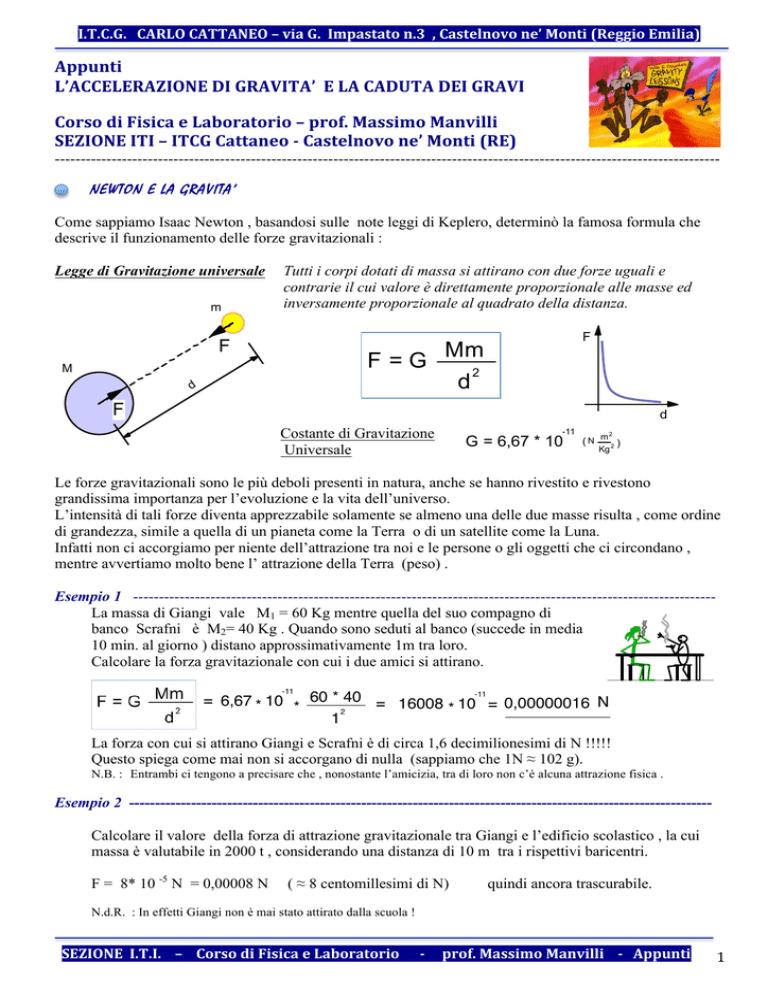
Legge di Gravitazione universale
m
Tutti i corpi dotati di massa si attirano con due forze uguali e
contrarie il cui valore è direttamente proporzionale alle masse ed
inversamente proporzionale al quadrato della distanza.
F
F
F = G Mm
2
d
M
d
F
d
Costante di Gravitazione
Universale
-11
G = 6,67 * 10
2
(N m 2 )
Kg
Le forze gravitazionali sono le più deboli presenti in natura, anche se hanno rivestito e rivestono
grandissima importanza per l’evoluzione e la vita dell’universo.
L’intensità di tali forze diventa apprezzabile solamente se almeno una delle due masse risulta , come ordine
di grandezza, simile a quella di un pianeta come la Terra o di un satellite come la Luna.
Infatti non ci accorgiamo per niente dell’attrazione tra noi e le persone o gli oggetti che ci circondano ,
mentre avvertiamo molto bene l’ attrazione della Terra (peso) .
Esempio 1 ----------------------------------------------------------------------------------------------------------------La massa di Giangi vale M1 = 60 Kg mentre quella del suo compagno di
banco Scrafni è M2= 40 Kg . Quando sono seduti al banco (succede in media
10 min. al giorno ) distano approssimativamente 1m tra loro.
Calcolare la forza gravitazionale con cui i due amici si attirano.
-11
-11
= 6,67 * 10 * 60 * 40 = 16008 10 = 0,00000016 N
*
2
1
La forza con cui si attirano Giangi e Scrafni è di circa 1,6 decimilionesimi di N !!!!!
Questo spiega come mai non si accorgano di nulla (sappiamo che 1N ≈ 102 g).
N.B. : Entrambi ci tengono a precisare che , nonostante l’amicizia, tra di loro non c’è alcuna attrazione fisica .
Esempio 2 ----------------------------------------------------------------------------------------------------------------Calcolare il valore della forza di attrazione gravitazionale tra Giangi e l’edificio scolastico , la cui
massa è valutabile in 2000 t , considerando una distanza di 10 m tra i rispettivi baricentri.
F = 8* 10 -5 N = 0,00008 N
( ≈ 8 centomillesimi di N)
quindi ancora trascurabile.
N.d.R. : In effetti Giangi non è mai stato attirato dalla scuola !
SEZIONEI.T.I.–CorsodiFisicaeLaboratorio-prof.MassimoManvilli-Appunti
1
I.T.C.G.CARLOCATTANEO–viaG.Impastaton.3,Castelnovone’Monti(ReggioEmilia)
Il valore della costante G fu ricavato nel 1798, con notevole precisione, dal fisico scozzese
Henry Cavendish, che riuscì a realizzare un esperimento passato alla storia come “La pesata
della Terra” in quanto riuscì a determinare la densità media del nostro pianeta.
H.Cavendish
Isaac Newton fu il primo a capire che le leggi della meccanica terrestre e
quelle della meccanica celeste dovevano essere le medesime.
La legge Fondamentale della Dinamica quindi doveva valere per tutti i tipi di forze ,
compresa la forza di gravità.
In questo caso è possibile esprimere il peso come il prodotto della massa del corpo per
l’accelerazione prodotta dalla gravità stessa :
Fp = ma
I. Newton
Confrontando le due espressioni della stessa grandezza, tenendo conto che devono essere equivalenti ,
possiamo osservare che :
Fp = G M m
2
d
l’accelerazione prodotta dalla forza
di gravità corrisponde a :
Fp = m a
A
B
R
R'
a = g = G M2
d
Per noi che viviamo sulla superficie terrestre la distanza dal centro della terra
corrisponde al raggio del pianeta (approssimativamente considerato sferico) e non
può variare di molto .
R = distanza dal centro della terra di un corpo che si trova a livello del mare
= 6378 Km = 6,378 *106 m (raggio medio terrestre)
R’ = distanza dal centro della terra di un corpo che si trova sulla cima
dell’Everest = 6378 + 8,8 Km = 6,3868 *106 m
Massa della terra M = 5,98*1024 Kg
Se calcoliamo il valore dell’accelerazione di gravità relativa alle due posizioni precedenti troviamo :
g(A) = 9,805 m/s2
g(B) = 9,778 m/s2
Come risulta evidente la differenza è molto piccola anche se misurabile.
I due valori calcolati inoltre non tengono conto di alcuni elementi che influiscono sul valore effettivo di
questa grandezza.
Bisogna infatti considerare che il valore dell’accelerazione di gravità varia al variare della latitudine
principalmente per due motivi :
1 – La terra non è perfettamente sferica ma “schiacciata” ai
poli , per cui la distanza dal centro è massima
all’equatore .
A g(A)
B
g(B)<g(A)
Ra
2 – La rotazione terrestre produce una “forza centrifuga”
diretta verso l’esterno, cioè opposta alla attrazione della
terra, che presenta il suo valore massimo all’equatore e
si annulla ai poli. Questa “forza apparente” effetto
dell’inerzia determina una diminuzione del peso dei corpi
quindi della accelerazione di gravità .
Rb
Rc
C
g(C)<g(B)<g(A)
SEZIONEI.T.I.–CorsodiFisicaeLaboratorio-prof.MassimoManvilli-Appunti
2
I.T.C.G.CARLOCATTANEO–viaG.Impastaton.3,Castelnovone’Monti(ReggioEmilia)
Entrambi questi effetti determinano una diminuzione del valore della accelerazione di gravità all’equatore
rispetto a quello relativo ai poli.
Il valore di g , a livello del mare , varia da 9,7799 m/s2 all’equatore a 9,83217 m/s2 ai poli .
Per questo motivo si considera normalmente un valore medio dell’accelerazione di gravità che approssima
il valore di g a livello del mare ad una latitudine di 45,5° , pari a :
g=
9,8066 m2
s
≈
9,8
m
2
s
Il calcolo eseguito per la Terra può essere esteso agli altri corpi celesti, come la Luna ed i pianeti; ogni
pianeta in base alle proprie dimensioni ed alla propria massa è caratterizzato da un valore particolare della
accelerazione di gravità.
3,701 m/s2
8,87 m/s2
3,72 m/s2
22,88 m/s2
1,622 m/s2
Mercurio
Venere
Marte
Giove
Luna
Mercurio – Venere – Terra – Marte
L’espressione dell’accelerazione ricavata dalla Legge di Gravitazione Universale non
contiene alcun elemento relativo al corpo sottoposto all’azione della gravità, ma dipende
solamente dalla massa e dalle dimensioni del pianeta.
g= G
M
2
d
Questo indica che l’accelerazione di gravità sulla superficie terrestre è la stessa per tutti i corpi,
indipendentemente dalla loro massa e quindi dal loro peso.
Quest’ultima affermazione può apparire falsa alla luce di ciò che vediamo accadere intorno a noi, in
quanto sembra che gli oggetti pesanti cadano “più velocemente” di quelli leggeri.
Si può dimostrare che la differenza di comportamento è dovuta solamente all’azione resistente dell’aria.
Newton , per verificare che tutti i corpi per effetto della sola gravità, cadono nello stesso modo, ideò un
famoso esperimento.
Il Tubo di Newton
:
IL TUBO DI NEWTON
Si tratta di un tubo di vetro contenente un chiodino ed una piuma.
Capovolgendo il tubo si può osservare che il chiodino raggiunge il fondo
molto prima della piuma.
Dopo aver estratto, l’aria tramite una pompa apposita, si può ripetere
l’esperienza verificando che chiodino e piuma cadono assieme, raggiungendo
il fondo nello stesso tempo.
Apollo 15
:
Con l'aria
Senza aria
In epoca moderna una verifica qualitativa di questo fenomeno è stata condotta
dagli astronauti della navicella Apollo 15, dopo l’atterraggio sulla Luna. E’
disponibile un filmato in cui un astronauta lascia cadere dalla stessa altezza un
attrezzo metallico ed una piuma.
In assenza di atmosfera i due corpi cadono esattamente nello stesso modo,
toccando il terreno assieme. Interessante il commento finale dell’astronauta
che , con il tipico accento americano , dice : “ Mister Galileo was correct ! “
Filmato Apollo 15
SEZIONEI.T.I.–CorsodiFisicaeLaboratorio-prof.MassimoManvilli-Appunti
3
I.T.C.G.CARLOCATTANEO–viaG.Impastaton.3,Castelnovone’Monti(ReggioEmilia)
Infatti Galileo, prima di Newton, aveva già intuito che le differenze nella velocità di caduta libera di
oggetti di peso diverso erano dovute alla resistenza del mezzo in cui il corpo si muoveva (nel caso più
comune l’aria), basandosi su ragionamenti e deduzioni veramente acute.
GALILEO E LA CADUTA DEI GRAVI
Con il termine “grave” si intende un corpo dotato di peso ; la parola “grave” infatti è di
origine greca e significa “corpo pesante”.
Aristotele riteneva che un oggetto pesante in caduta libera arrivasse al suolo, per effetto
del proprio peso, più rapidamente di uno leggero lasciato cadere dalla stessa altezza .Al
contrario, Galileo Galilei (osservatore più attento di Aristotele!!) era dell'opinione che tutti i corpi, pesanti o
leggeri, dovessero impiegare lo stesso tempo per arrivare al suolo a causa del proprio peso, spiegando le
piccole differenze riscontrate sui tempi di caduta con l'azione di disturbo esercitata sul moto dell'oggetto da
altri fattori esterni. Egli cercò quindi, attraverso prove sperimentali e ragionamenti speculativi, di
dimostrare la fondatezza della sua teoria sulla caduta dei gravi .
Un esperimento si trova descritto nell'opera “Discorsi e Dimostrazioni
matematiche attorno a due nuove scienze attinenti alla Meccanica e i
Movimenti Locali": ".. Ma io, signor Simplicio, che n'ho fatto prova, vi assicuro
che una palla di artiglieria, che pesi cento, dugento e anco più libbre, non
anticiperà d'un palmo solamente l'arrivo in terra della palla d'un moschetto,
che ne pesi una mezza, venendo anco dall'altezza di dugento braccia... Ia
maggiore anticipa due dita la minore, cioè che quando la grande percuote la
terra, I'altra ne è lontana due dita."
La leggenda vuole che Galileo abbia fatto cadere dalla torre pendente di Pisa
due palle, una di ferro e l'altra di legno, delle stesse dimensioni ed abbia così convinto gli increduli che le
due palle toccavano il suolo quasi contemporaneamente. Vera o no che sia questa leggenda, è un fatto
accertato che Galileo compì numerose osservazioni per dimostrare che :
"la velocità dei mobili della stessa materia, disegualmente gravi, movendosi per un istesso mezzo, non
conservano altrimenti la proporzione della gravità loro, assegnatali da Aristotele..." .
Egli utilizzò anche un tipico ragionamento deduttivo per dimostrare che la
velocità di caduta di un corpo non può essere proporzionale al suo peso :
"Ma se questo è, ed è insieme vero che una pietra grande si muove, per esempio,
con otto gradi di velocità, ed una minore con quattro, adunque congiungendole
ambedue insieme, il composto di loro si muoverà con velocità minore di otto
gradi: ma le due pietre, congiunte insieme, fanno una pietra maggiore che quella
prima, che si muoveva con otto gradi di velocità; adunque questa maggiore si
muove meno velocemente che la minore; che è contro vostra supposizione."
Ma perché, allora, nella maggior parte dei casi osservati i corpi pesanti cadono più
in fretta, anche se solo di poco, di quelli più leggeri? Galileo non ha dubbi in
proposito, la ragione va cercata nella resistenza dell'aria:
"... e perché solo uno spazio del tutto voto d'aria e di ogni altro corpo, ancorché tenue e cedente, sarebbe
atto a sensatamente mostrarci quello che cerchiamo, già che manchiamo di cotale spazio, andremo
osservando ciò che accaggia ne i mezzi più sottili e meno resistenti, in comparazione di quello che si vede
accadere negli altri meno sottili e più resistenti. Se noi troviamo, in fatto, i mobili differenti di gravità
meno e meno differir di velocità secondo che i mezzi più e più cedenti si troveranno, ..., parmi che potremo
con molto probabil conietture credere che nel vacuo sarebbero le velocità loro del tutto eguali."
SEZIONEI.T.I.–CorsodiFisicaeLaboratorio-prof.MassimoManvilli-Appunti
4
I.T.C.G.CARLOCATTANEO–viaG.Impastaton.3,Castelnovone’Monti(ReggioEmilia)
IL PESO
Nota la massa di un corpo è facile risalire al valore del suo peso, ovvero della forza con cui la
terra lo attrae verso il suo centro .
E’ sufficiente applicare la Legge fondamentale della Dinamica inserendo il valore medio ,
ormai noto, della accelerazione di gravità.
Fp = m g
Esempio 3 ------------------------------------------------------------------------------------------------La massa di Giangi vale M = 60 Kg , quanto vale il suo peso sulla Terra ?
Fp = mg = 60* 9,8 = 588 N
Sapendo che il valore dell’ accelerazione di gravità lunare è g(L) = 1,622 m/s2 calcolare il
peso di Giangi sulla Luna.
Fp(L) = m*g(L) = 60 * 1,622 = 97,32 N
La massa di Giangi è sempre la stessa mentre l’accelerazione di gravità vale circa un sesto di
quella terrestre, per cui sulla luna il peso di Giangi si riduce a circa 1/6 ( … senza dieta!!).
Esempio 4 ----------------------------------------------------------------------------------------------------------------Qual è la differenza tra il peso di Giangi all’equatore ed al polo nord, calcolato a livello del
mare?
Equatore
Fp = mg = 60* 9,7799 = 586,8 N
Polo Nord
Fp = mg = 60* 9,8322 = 589,9 N
La differenza è di 3,1 N ovvero poco più di 3 “etti “ ( circa lo 0,5%).
-----------------------------------------------------------------------------------------------------------------------
IL MOTO DI CADUTA DEI GRAVI
v0
v = v0 + g t
S = v0 t +
S
1
2
g = 9,8 m/s2
v
gt
2
Con il termine “caduta dei gravi” si intende il
moto di caduta libera di un corpo dotato di peso .
Il peso di un corpo in caduta vicino alla
superficie terrestre può essere considerato
costante , così come l’accelerazione di gravità.
Quindi un corpo sottoposto solamente all’azione della gravità,
nell’ipotesi che siano trascurabili le forze resistenti , in particolare
quella dell’aria, si muoverà di moto uniformemente accelerato con
accelerazione costante pari a g.
Per descriverne il movimento si possono quindi utilizzare le leggi del
moto uniformemente accelerato introducendo come valore della
accelerazione g.
Le leggi orarie del moto di caduta libera di un grave diventano quelle
riportate nella figura qui a fianco.
Il movimento di caduta libera di un corpo viene chiamato “Moto
naturalmente accelerato”
Naturalmente la presenza dell’aria determina un rallentamento della caduta con diminuzione della
accelerazione spesso non trascurabile.
SEZIONEI.T.I.–CorsodiFisicaeLaboratorio-prof.MassimoManvilli-Appunti
5
I.T.C.G.CARLOCATTANEO–viaG.Impastaton.3,Castelnovone’Monti(ReggioEmilia)
In presenza dell’aria possiamo esaminare qualitativamente il movimento
di un corpo in caduta libera .
Fp
Il corpo risulta soggetto a due forze : il peso, diretto verso il basso, e la
resistenza dell’aria (aerodinamica) di verso opposto.
Moto accelerato
Fp
>
R aria
R0
Mentre il peso può essere ritenuto costante, la resistenza dell’aria varia
oltre che in base alle dimensioni ed alla forma dell’oggetto, anche in
funzione della velocità.
V aumenta
Moto uniforme
Fp
=
R aria
Fp
R = - Fp
V=cost
Nella fase iniziale prevale il valore della forza peso, la risultante è diretta
verso il basso ed il corpo accelera.
Durante la caduta aumenta la velocità ed aumenta di conseguenza la
resistenza dell’aria.
Quando la resistenza dell’aria diventa uguale
ed opposta alla forza peso la risultante si
annulla e , da questo momento in poi, come
previsto dal 1° Principio della Dinamica, il
corpo prosegue a velocità costante.
Ogni corpo in caduta libera raggiunge una
propria velocità massima (detta anche
velocità limite) che dipende dalle sue
dimensioni e dalla sua forma, che influiscono
evidentemente sul valore della resistenza
aerodinamica.
v
velocità di
regime
t
IL TEOREMA DI TORRICELLI
Il teorema dovuto ad Evangelista Torricelli, che fu assistente di
Galileo Galilei, permette di calcolare in modo molto semplice ed
immediato la velocità raggiunta da un corpo in caduta libera, partito
da fermo, in base all’altezza di caduta, trascurando la resistenza
dell’aria.
v= gt
Poiché la velocità iniziale è nulla le leggi orarie del
2
1
moto naturalmente accelerato si semplificano :
h=
Dalla seconda legge si ricava :
2
t = 2h
g
t =
2h
g
h
2h
g
Sostituendo t nella prima legge oraria si ottiene :
v= g t= g
2
gt
v0 = 0
v
=
2
g 2h
g
=
2gh
SEZIONEI.T.I.–CorsodiFisicaeLaboratorio-prof.MassimoManvilli-Appunti
6
I.T.C.G.CARLOCATTANEO–viaG.Impastaton.3,Castelnovone’Monti(ReggioEmilia)
Esempio 5 ----------------------------------------------------------------------------------------------------------------Giangi , dopo aver fatto molte prove su Scrafni, ricoverato per
commozione cerebrale dopo la riuscita del lancio, lascia cadere
dal tetto della scuola un vaso di fiori in testa al suo prof.
preferito, che sta entrando dall’ingresso.
Sapendo che il vaso parte da un’altezza di 6,3 m rispetto alla
testa del prof. , calcolare la velocità con cui avverrà l’impatto.
v=
2gh
=
2 * 9,8 * 6,3
v0 = 0
= 11,11 m/s ≈ 40 Km/h
v
Calcolare il tempo di caduta del vaso .
t=
2h
g
=
(2* 6,3/9,8) = 1,13 s
Esempio 6 ----------------------------------------------------------------------------------------------------------------Scrafni vuole provare la sua nuova fionda.
Si posiziona con precisione e lancia il proiettile in perfetta verticale per vedere a che
altezza arriverà.
Il proiettile esce dalla fionda alla velocità di 39,2 m/s.
Calcolare l’altezza massima raggiunta dal proiettile rispetto all’ estremità superiore
della fionda, trascurando la resistenza dell’aria.
Hmax
y
Si tratta di un moto uniformemente decelerato; infatti sul proiettile , una volta che ha
lasciato la fionda, agisce la sola forza di gravità, diretta verso il basso, ovvero opposta
al movimento , che, come sappiamo, produce una accelerazione, in questo caso
V0
negativa, di -9,8 m/s2.
Mentre il proiettile si muove verso l’alto la sua velocità diminuisce di 9,8 m/s in ogni
secondo.
Conosciamo anche un altro dato del problema, non citato nel testo (un cosiddetto
“dato nascosto”) cioè il valore della velocità finale nel punto di massima
altezza raggiunta, che evidentemente vale V = 0 .
v = v0 - g t
Applichiamo quindi le leggi orarie del moto naturalmente accelerato.
In particolare dalla prima legge oraria è facile ricavare il tempo impiegato a
raggiungere la massima altezza :
v = v0 - g t
0 = 39,2 - 9,8 t
9,8 t = 39,2
t =
39,2
= 4,0 s
9,8
v
t = 0
g
Orasostituendoilvaloreditnella
secondaleggeorariaèpossibilecalcolare
ladistanzapercorsa,checoincideconil
valoredellamassimaaltezzaraggiunta.
x
2
S = v0 t - 1 g t
2
S = v0 t - 1 g t
2
2
Hmax = 39,2 * 4 -
2
1
9,8 * 4
*
2
Hmax = 156,8 - 78,4 = 78,4 m
Scrafnièabbastanzasoddisfatto.
NelfrattempoGiangitrascinaviaScrafniche,unpo’allucinatocomeal
solito,stavatranquillamenteosservandoilmovimentodelproiettile,
aspettandocheritornasseindietroperrecuperarlo,arischiodella
propriaincolumità.
SEZIONEI.T.I.–CorsodiFisicaeLaboratorio-prof.MassimoManvilli-Appunti
7
I.T.C.G.CARLOCATTANEO–viaG.Impastaton.3,Castelnovone’Monti(ReggioEmilia)
2° Metodo
N.B. :
questo esercizio può essere risolto agevolmente utilizzando il teorema di Torricelli.
Possiamo infatti considerare che , avendo trascurato la resistenza dell’aria , il percorso di ritorno del
proiettile risulta caratterizzato da velocità V0=0 m/s nel punto di massima altezza, accelerazione di 9,8 m/s2
provocata dalla gravità e velocità finale a terra di 39,2 m/s .
Si tratta evidentemente della situazione cui si riferisce il teorema di Torricelli.
E’ possibile allora utilizzare la formula di Torricelli, invertendola per calcolare
l’altezza massima raggiunta.
Elevando ambo i membri al quadrato :
Dividendo ambo i membri per 2g :
v=
2gH
2
v = 2gH
2
v = 2gH
2g
2g
2
si ottiene :
v
H =
2g
Nel nostro caso utilizzando i dati dell’esercizio si ottiene immediatamente :
2
39,2
= 78,4 m
H =
2•9,8
--------------------------------------------------------------------------------------------------------------------
SEZIONEI.T.I.–CorsodiFisicaeLaboratorio-prof.MassimoManvilli-Appunti
8












