esercizi - Edutecnica

Edutecnica.it – Circuiti risonanti – esercizi risolti
1
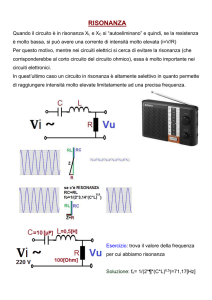
Circuiti Risonanti serie:Riepilogo delle regole
Sono circuiti costituiti da una bobina L, una resistenza R che
può anche solamente coincidere con la resistenza serie
derivante dalle perdite della bobina Rb ed una capacità C
posti in serie, alimentati da un generatore E che in genere
ha una resistenza interna Ri. Se consideriamo RT=R+Rb+Ri.
Si può fare riferimento al circuito illustrato.
Si usa la seguente nomenclatura:
ω0 , f0 = pulsazione e frequenza di risonanza
B=banda passante del circuito risonante
f1,f2=frequenze di taglio a cui la corrente si riduce a
I0
con I0 la corrente in condizioni di
2
risonanza.
Qb= coefficiente di qualità della bobina Qb =
Q= coefficiente di risonanza del circuito Q =
ω0 L
Rb
ω0 L
RT
dove RT è la resistenza totale vista ai morsetti
dell’induttanza L col generatore E cortocircuitato.
Valgono le relazioni:
ω0 =
Q=
1
LC
ω0 L
RT
=
per ω = ω0
bobina.
da cui
f0 =
1
2π LC
1
ω0CRT
B = f 2 − f1 =
I0 =
f0
Q
E
RT
si ha VC = VL = QE essendo VC e VL le tensioni ai capi del condensatore e della
Per ω=ω0 il comportamento del circuito è resistivo
Per ω<ω0 il comportamento del circuito è capacitivo
Per ω>ω0 il comportamento del circuito è induttivo
1
Edutecnica.it – Circuiti risonanti – esercizi risolti
2
Circuiti risonanti parallelo: Riepilogo delle regole
Sono costituiti dal parallelo fra un’induttanza L (che ha in serie una resistenza Rb) ed una capacità
C. Vengono alimentati da un generatore di corrente I0 che ha in parallelo una sua resistenza interna
R0 secondo lo schema illustrato.
Valgono le stesse notazioni viste per i circuiti risonanti serie, per
f1,f2= frequenze a cui la tensione si riduce a
0, f0
B e Qb, inoltre:
V0
con V0, tensione ai capi del parallelo in condizioni
2
di risonanza.
Rp0= Resistenza parallela della bobina R p0 =
ω02 L2
Rb
= Qbω0 L = Qb2 Rb (la resistenza che può essere
messa in parallelo al remo induttivo eliminando la Rb)
RT=Resistenza complessiva del circuito risonante, uguale alla resistenza vista ai morsetti del
condensatore C con Ii aperto. Quando al posto di Rb venga posta Rp0.
Q= coefficiente di risonanza del circuito Q =
RT
ω0 L
Si hanno inoltre, le relazioni:
V 0 = I 0 RT
Q=
RT
= ω0 CRT
ω0 L
Per ω= ω 0: IC=IL=QIi ; Si può constatare che
Per ω = ω 0 il comportamento del circuito è resistivo
Per ω < ω 0 il comportamento del circuito è induttivo (contr.al caso serie)
Per ω > ω 0 il comportamento del circuito è capacitivo (contr.al caso serie)
2
Edutecnica.it – Circuiti risonanti – esercizi risolti
Esercizio no.1
▄
3
soluzione a pag.5
Un generatore con resistenza interna Ri=50kΩ, alimenta alla frequenza di risonanza f0=12kHz, un
circuito RCL parallelo formato da una bobina di induttanza L=40mH e Qb=14.
Calcola:
- La capacita C del condensatore
- Il coefficiente di risonanza Q
- La banda passante B
Esercizio no.2
▄
soluzione a pag.6
Il circuito risonante parallelo illustrato:
risuona alla frequenza di 500kHz e alla risonanza presenta una resistenza Rp0=20kΩ con un
coefficiente di qualità della bobina Qb=25.
Determina l’induttanza della bobina, la sua resistenza serie, la capacità e la banda passante del
circuito .
Esercizio no.3
▄
soluzione a pag.7
Un circuito risonante serie, risuona alla frequenza di 1MHz e quando la frequenza differisce da
quella di risonanza di 10kHz la corrente si riduce al 70% della corrente massima (di risonanza).
Calcola il coefficiente di risonanza Q, l’induttanza e la resistenza serie complessiva del circuito,
sapendo che C=100pF.
3
Edutecnica.it – Circuiti risonanti – esercizi risolti
Esercizio no.4
4
▄
soluzione a pag.8
Nel circuito illustrato si trovi alla risonanza l’induttanza e il fattore di qualità Qb della bobina
sapendo che il coefficiente di risonanza Q=20.
E = 25V
Ri = 15Ω
Rx = 100 kΩ
C = 1000 pF
f0 = 159 Hz
Esercizio no.5
▄
soluzione a pag.9
Un circuito risonante serie risulta avere una banda passante B=10kHz ed un coefficiente di
risonanza Q=100.
Sapendo che la resistenza serie del circuito è di 10Ω, calcolare il valore dell’induttanza L e della
capacità C.
4
Edutecnica.it – Circuiti risonanti – esercizi risolti
5
Esercizio no.1
Un generatore con resistenza interna Ri=50kΩ, alimenta alla frequenza di risonanza f0=12kHz, un
circuito RCL parallelo formato da una bobina di induttanza L=40mH e Qb=14.
Calcola:
- La capacita C del condensatore
- Il coefficiente di risonanza Q
- La banda passante B
Esercizio no.1:soluzione
Alla risonanza ω0 C =
R p0 =
ω02 L2
Rb
1
ω0 L
→ C=
1
ω02 L
=
1
= 4 ,4 nF
( 2π ⋅ 12 ⋅ 10 3 )2 ⋅ 40 ⋅ 10 − 3
= Qbω0 L = 14( 2π ⋅ 12000 ) ⋅ 40 ⋅ 10 − 3 = 42223Ω = 42kΩ
Dal disegno si ha che la resistenza totale del circuito è
RT = Ri // R p0 = 23kΩ
Q=
RT
23000
=
= 7 ,5
ω0 L 2π ⋅ 12000 ⋅ 40 ⋅ 10 − 3
B=
f0 12000
=
= 1573Hz
Q
7 ,5
5
Edutecnica.it – Circuiti risonanti – esercizi risolti
6
Esercizio no.2
Il circuito risonante parallelo illustrato:
risuona alla frequenza di 500kHz e alla risonanza presenta una resistenza Rp0=20kΩ con un
coefficiente di qualità della bobina Qb=25.
Determina l’induttanza della bobina, la sua resistenza serie, la capacità e la banda passante del
circuito .
Esercizio no.2:soluzione
R p0 =
ω02 L2
Rb
= Qbω0 L = Qb2 Rb
20 ⋅ 10 3 = 25 ⋅ 2π ⋅ 500 ⋅ 10 3 L → L =
20
= 2 ,546 ⋅ 10 − 4 H = 254 ,6 ⋅ 10 − 6 = 254 ,6 µH
25 ⋅ 2π ⋅ 500
dalla stessa relazione si ottiene: R p0 = Qb2 Rb → Rb =
R p0
Qb2
=
20.000
= 32Ω
25 2
alla risonanza si ha :
1
= ω0 C →
ω0 L
C=
1
Lω02
=
1
= 3 ,97 ⋅ 10 −10 ≅ 400 pF
3 2
−6
254 ,6 ⋅ 10 ( 2π ⋅ 500 ⋅ 10 )
Q=
RT
= ω0 CRT = ω0 CR p0 = 2π ⋅ 500 ⋅ 10 3 ⋅ 400 ⋅ 10 − 12 ⋅ 20 ⋅ 10 3 = 25 ≡ Qb
ω0 L
B=
f0 500
=
= 20 kHz
Q
25
6
Edutecnica.it – Circuiti risonanti – esercizi risolti
7
Esercizio no.3
Un circuito risonante serie, risuona alla frequenza di 1MHz e quando la frequenza differisce da
quella di risonanza di 10kHz la corrente si riduce al 70% della corrente massima (di risonanza).
Calcola il coefficiente di risonanza Q, l’induttanza e la resistenza serie complessiva del circuito,
sapendo che C=100pF.
Esercizio no.3:soluzione
Ovviamente per le considerazioni che valgono sulla larghezza di banda,sarà:
f1 = 1000 − 10 = 990 kHz
f1 = 1000 + 10 = 1010 kHz
B = f 2 − f1 = 1010 − 990 = 20 kHz
poi dalla
B=
f0
Q
si ha:
f0
106
Q=
=
= 50
B 20 ⋅ 10 3
per cui se f0 =
L=
Q=
1
2π LC
1
2
12
4π 10 ⋅ 10
ω0 L
RT
→
−10
→
LC =
1
1
→ L= 2 2
2π ⋅ f0
4π f0 C
= 253 ⋅ 10 −6 H = 253 µH
dato che
2π ⋅ f0 L 2π ⋅ 106 253 ⋅ 10 −6
RT =
=
=
= 32 Ω
Q
Q
50
ω0 L
7
Edutecnica.it – Circuiti risonanti – esercizi risolti
8
Esercizio no.4
Nel circuito illustrato si trovi alla risonanza l’induttanza e il fattore di qualità Qb della bobina
sapendo che il coefficiente di risonanza Q=20.
E = 25V
Ri = 15Ω
Rx = 100 kΩ
C = 1000 pF
f0 = 159 Hz
Esercizio no.4:soluzione
Purtroppo ci tocca calcolare l’impedenza equivalente fra il condensatore e la resistenza Rx.
1
j( 100 + j )10 5
jωC 10 5 ( − j10 3 ) − j10 5
=
=
=
≅−
= 10 − j1000
5
3
4
1
100
−
j
10
−
j
10
10
R+
j ωC
R⋅
Z eq
Si può notare come la capacità equivalente abbia lo stesso valore di C. Il circuito si trasforma nel
modo seguente:
Ovviamente, alla risonanza,
1
ω0 L =
ω0 Ceq
Q=
ω0 L
RT
=
ω0 L
Rb + Ri + Req
segue per Qb: Qb =
ω0 L
Rb
→
Rb =
→
ω0 L − Q( Ri + Req )
Q
1
10 3
L= 2
=
= 1mH
ω0 Ceq 10 6
=
10 3 − 20( 15 + 10 )
= 25Ω
20
10 3
=
= 40
25
8
Edutecnica.it – Circuiti risonanti – esercizi risolti
9
Esercizio no.5
Un circuito risonante serie risulta avere una banda passante B=10kHz ed un coefficiente di
risonanza Q=100.
Sapendo che la resistenza serie del circuito è di 10Ω, calcolare il valore dell’induttanza L e della
capacità C.
Esercizio no.5:soluzione
Basandosi sulle relazione:
B=
f0
Q
→
f 0 = BQ = 10 4 ⋅ 10 2 = 10 6 Hz
ω0 = 2π f0 = 2π ⋅ 10 6 = 6 ,28 ⋅ 10 6 rad / s
Q=
ω0 L
RT
→ L=
ma è anche Q =
RT Q
ω0
1
ω0 CRT
=
10 ⋅ 100
= 0,159 ⋅ 10 - 3 = 0 ,159 mH = 159 µH
6
6 ,28 ⋅ 10
→
C=
1
1
=
= 0 ,159 ⋅ 10 − 9 F
6
2
ω0 QRT 6 ,28 ⋅ 10 ⋅ 10 ⋅ 10
Quindi è C = 0 ,159 nF = 159 pF
9