Cap. 12 - Superconduttività.
Introduzione.
La scoperta della Superconduttività risale al 1911. Da allora ha vissuto un lungo
periodo in cui è rimasta confinata all’interno degli ambienti accademici pur
continuando a dare un grande impulso alla fisica dello stato solido del Novecento. La
necessità di raggiungere temperature prossime allo zero assoluto per ottenere la
transizione da conduttore a superconduttore ne aveva precluso le enormi potenzialità
e limitato l’uso a pochi campi. A partire dal 1986, la scoperta dei superconduttori ad
alta temperatura di transizione (maggiore di 77 K, temperatura di liquefazione
dell’azoto) ha permesso l’uso dei superconduttori in moltissime applicazioni
tecnologiche. La strada verso la superconduttività fu aperta dallo studio sulla
refrigerazione a basse temperature. I maggiori progressi in questo campo furono
fatti alla fine del XIX secolo. Lo scopo principale della lunga carriera del fisico
olandese Heike Kammerlingh Onnes fu quello di esplorare le bassissime temperature.
Il 10 luglio 1908 egli riuscì nel formidabile compito di liquefare l’elio, ultimo tra i gas
inerti a essere condensato, portandolo a 4 K. Quel giorno solo pochi millilitri di elio
furono liquefatti da Onnes ma ciò aprì la strada all’esplorazione di regioni di
temperatura precedentemente irraggiungibili. Il fisico olandese cominciò ad
investigare le proprietà elettriche dei metalli a temperature molto basse e nel 1911 la
superconduttività fu scoperta per la prima volta. A quel tempo vi erano due ipotesi a
riguardo: la prima voleva che gli elettroni fossero ‘congelati’ dall’abbassarsi della
temperatura (tesi che vedeva tra i capifila Lord Kelvin), la seconda sosteneva il
raggiungimento di un non ben definito valore minimo della resistenza (Onnes). La
seconda ipotesi suggeriva una diminuzione della resistenza all’abbassarsi della
temperatura permettendo alla corrente un flusso imperturbato o quasi. Onnes fece
passare una corrente attraverso un filo di mercurio purissimo misurando la resistenza
al diminuire della temperatura. Non si osservò né il livellamento in basso della
resistenza né tanto meno il congelamento degli elettroni. A 4.2 K la resistenza
scomparve totalmente. Onnes affermò che “il mercurio era passato in un nuovo stato
che in base alle straordinarie proprietà elettriche può essere indicato come stato
superconduttivo”. L’esperimento non lasciava dubbi circa la scomparsa della resistenza
nel filo di mercurio.
V. Augelli, Fisica degli Stati Condensati, Cap.12 – Superconduttività
1
Lo scienziato intuì subito l’importanza della scoperta anche da un punto di vista
commerciale: un conduttore privo di resistenza può trasportare corrente a qualsiasi
distanza senza perdite! In uno dei suoi esperimenti Onnes fece passare una corrente
in un filo chiuso raffreddato a 4 K. Un anno dopo la corrente ancora fluiva nel filo
senza perdite misurabili. Onnes trovò che i superconduttori permettono l’esistenza di
quelle che lui chiamò correnti persistenti, cioè correnti elettriche che continuano a
fluire senza una differenza di potenziale che le sostenga. Il fisico olandese vinse il
premio Nobel per la Fisica nel 1913. La resistenza nulla al flusso di corrente elettrica
non rimase l’unico motivo di meraviglia; il comportamento dei metalli superconduttori
in un campo magnetico esterno si rivelò altrettanto sbalorditivo. Nel 1933 due fisici
tedeschi, Karl Walther Meissner e Robert Ochsenfeld, scoprirono che i
superconduttori, oltre ad essere perfetti conduttori di elettricità, sono anche dei
perfetti materiali diamagnetici, capaci cioè di espellere il flusso magnetico che
contengono quando vengono raffreddati al di sotto della propria temperatura di
transizione. La completa espulsione del flusso magnetico è nota oggi sotto il nome di
Effetto Meissner. L’Effetto Meissner avviene solo se il campo magnetico è
relativamente piccolo: se questo è troppo grande penetra nel superconduttore e il
metallo perde il suo stato superconduttivo. Assieme all’assenza di resistenza, è stata
proprio questa capacità di espellere il flusso magnetico a suscitare gli enormi interessi
di ricerca nel campo della superconduttività.
Fino agli anni ‘50 le evidenze
sperimentali sulla superconduttività correvano più velocemente dei modelli teorici che
potessero spiegare cosa accadeva a livello microscopico. I modelli quantistici
sviluppati negli anni trenta potevano spiegare la conduttività nei metalli normali, ma
non lo stato superconduttivo. Fu allora che due studiosi russi, Vitalj L. Ginzburg e Ley
D. Landau, svilupparono una teoria fenomenologica della superconduttività. Osservando
ciò che avveniva durante la transizione dallo stato normale a quello di
superconduzione, i due scienziati riuscirono a formulare una serie di equazioni che
descrivevano il fenomeno; non si riusciva però a spiegare a livello microscopico perché
questo si verificasse. Nel 1957 gli scienziati cominciarono a scardinare il mistero che
attanagliava il fenomeno superconduttivo. Tre fisici americani dell’Università
V. Augelli, Fisica degli Stati Condensati, Cap.12 – Superconduttività
2
dell’Illinois, John Bardeen, Leon Cooper e Robert Schrieffer svilupparono un modello
per la comprensione dei fenomeni fisici microscopici che accadono nello stato
superconduttivo. Il modello è basato su considerazioni di meccanica quantistica e
l’idea di base prevede che in un superconduttore gli elettroni condensino in uno stato
quantistico di energia minima e viaggino collettivamente e coerentemente. Secondo
questo modello gli elettroni di conduzione si propagano senza incontrare resistenza
perché si muovono in coppie, le cosiddette coppie di Cooper. Lo stato superconduttivo
è caratterizzato dalla temperatura critica (o temperatura di transizione), insieme al
campo magnetico critico e alla densità di corrente critica. Per valori della temperatura
o del campo magnetico al di sopra dei valori critici, le fluttuazioni termiche o
quantistiche distruggono le coppie di Cooper e di conseguenza lo stato di
superconduzione del metallo. Nel 1972 i tre scienziati vinsero il premio Nobel per la
Fisica e da allora la loro teoria microscopica della superconduttività è indicata come
teoria BCS. L’evoluzione nel tempo delle conoscenze sulla superconduttività aveva
portato ad una classificazione dei materiali superconduttori in due tipi, indicati
semplicemente con I e II. I superconduttori di tipo I tendono ad essere
superconduttori in condizioni di bassa temperatura e debole campo magnetico; se il
campo raggiunge l’intensità critica (la quale dipende dal materiale), entra nel materiale
distruggendo lo stato di superconduzione. I superconduttori di tipo II sono molto più
utili: essi rimangono nello stato di superconduzione anche dopo la penetrazione del
campo magnetico. I superconduttori di tipo II possono sopportare campi molto forti fino a quello che è chiamato campo critico superiore - e quindi trasportare correnti
più intense. Negli anni cinquanta il fisico russo Aleksej A. Abrikosov pubblicò la
teoria di base sul comportamento di un superconduttore convenzionale di II tipo in
presenza di un campo magnetico.
Prendendo spunto dal lavoro di Ginzburg e Landau, Abrikosov riuscì a dimostrare che
il comportamento magnetico di un superconduttore di tipo II sotto la temperatura
critica dipende dall’intensità del campo applicato e dalla temperatura. Tale relazione
può essere rappresentata da un diagramma di fase magnetico, il quale mostra che un
superconduttore convenzionale ha tre stati magnetici distinti. Abrikosov, attualmente
presso gli Argonne National Laboratories di Chicago, ha ottenuto un altro importante
V. Augelli, Fisica degli Stati Condensati, Cap.12 – Superconduttività
3
risultato: ha previsto teoricamente l’ordinamento dei vortici di supercorrenti
(presenti nei superconduttori di tipo II) in un reticolo periodico. Questi vortici
racchiudono quantità discrete di campo magnetico che penetra nel superconduttore.
La configurazione di minima energia per una tale schiera di linee di flusso (vista
stando sopra la superficie) è quella di un reticolo triangolare. Il reticolo di Abrikosov
è stato osservato sperimentalmente con una struttura a base triangolare e la sua
esistenza e stabilità hanno importanti conseguenze per le applicazioni tecnologiche.
Nel 1962, Brian D. Josephson, ricercatore all’Università di Cambridge, studiò due
superconduttori separati da uno strato di materiale isolante che agisce da barriera al
flusso di corrente. Ebbene, nel caso lo spessore della barriera non sia troppa grande
le coppie di Cooper possono passare per effetto tunnel attraverso la barriera senza
dividersi, e quindi la giunzione funziona come un debole superconduttore. La corrente
critica vale a dire la supercorrente massima che può attraversare la giunzione dipende
dalla dimensione della giunzione, dal tipo di materiale superconduttore e dalla
temperatura. Questo fenomeno, che prende il nome di Effetto Josephson, fu
verificato alcuni mesi più tardi da Philip W. Anderson e John M. Rowell dei Bell
Telephone Laboratories. Nel 1973 Josephson ricevette il premio Nobel per la Fisica in
onore dell’effetto che era ormai universalmente riconosciuto come effetto
Josephson. Nel 1986 J. Georg Bednorz e K. Alex Muller nei laboratori IBM di Zurigo
conducevano esperimenti su una particolare classe di ceramiche a base di ossido di
rame, chiamate perovskiti. I due avevano sperimentato centinaia di differenti
composti ossidi. Lavorando con ceramiche di lantanio, bario, rame e ossigeno (formula
chimica La2-xBaxCuO4) essi trovarono evidenze di superconduttività a 35 K. Subito la
comunità scientifica cominciò a lavorare con i nuovi materiali che si candidavano ad
essere una nuova classe di superconduttori di II tipo. Nel febbraio del 1987 fu
individuata una ceramica perovskite in grado di supercondurre a 90 K (formula chimica
YBa2Cu3O7). Questa scoperta fu molto importante in quanto da quel momento divenne
possibile usare come mezzo refrigerante l’azoto liquido (punto di ebollizione a 77 K),
sostanza comunissima e facile da produrre. Viste le temperature in gioco si cominciò
ad indicare questi materiali come Superconduttori ad alta temperatura critica (HTcS
- High Critical Temperature Superconductors). Al momento sono in corso numerosi
sforzi economici e scientifici nel campo degli HTcS. La facilità di raffreddare i nuovi
superconduttori ha notevolmente influenzato gli sforzi nello sviluppo di nuovi
materiali, nelle tecniche di fabbricazione e nelle ricerche teoriche per tener conto
delle molteplici proprietà dei nuovi superconduttori ceramici. Inoltre le applicazioni
elettriche e magnetiche di potenza come le applicazioni elettroniche sono ora
accessibili economicamente e in pratica. I fullereni, come le ceramiche
superconduttrici, sono una scoperta recente. Nel 1985 R.F. Curl e R.E. Smalley della
Rice University in Houston e H.W. Kroto dell’Università of Sussex di Brighton, in
Inghilterra, sintetizzarono accidentalmente tale composto organico. Il fullerene,
chiamato anche ‘buckyball’ è stabile a livello molecolare quando 60 atomi di carbonio si
uniscono in pentagoni ed esagoni a formare una sfera chiusa.
V. Augelli, Fisica degli Stati Condensati, Cap.12 – Superconduttività
4
La scoperta della superconduttività nei fullereni intercalati con metalli alcalini
avvenne nel 1991: R. Huddon e i Bell Labs annunciarono che il composto K3C60
superconduceva alla temperatura di 18 K. Una Tc di 52 K è stata riportata negli ultimi
mesi del 2000 da H. Schon, C. Kloc e B. Batlogg, per un composto di C60 . La
superconduttività ci riserva continue sorprese: lo scorso 10 gennaio 2001, J. Akimitsu
della Aoyama-Gakuin University (Tokyo) e collaboratori annunciano al simposio sugli
ossidi dei metalli di transizione la scoperta di una transizione superconduttiva a Tc =
39 K nel diboruro di magnesio ( formula chimica MgB2).
Si tratta di un caso particolare o una nuova classe di superconduttori sta per essere
scoperta? Andrea Perali e Jeffrey Neaton della Rutgers University prevedono che il
drogaggio di MgB2 con sodio e calcio possa innalzare la temperatura critica intorno ai
50 K.
V. Augelli, Fisica degli Stati Condensati, Cap.12 – Superconduttività
5
Premi Nobel per la Superconduttività
Onnes (1913)
"For his investigations on the properties of matter at low temperatures which led,
inter alia, to the production of liquid helium"
Bardeen, Cooper, Schrieffer (1972)
"For their jointly developed theory of superconductivity, usually called the BCStheory"
V. Augelli, Fisica degli Stati Condensati, Cap.12 – Superconduttività
6
Josephson (1973)
"For his theoretical predictions of the properties of a supercurrent through a tunnel
barrier, in particular those phenomena which are generally known as the Josephson
effects"
Bednorz and Muller (1987)
"For their important break-through in the discovery of superconductivity in ceramic
materials"
V. Augelli, Fisica degli Stati Condensati, Cap.12 – Superconduttività
7
Abrikosov, Ginzburg, Leggett (2003)
For "decisive contributions concerning
superconductivity and superfluidity."
two
phenomena
V. Augelli, Fisica degli Stati Condensati, Cap.12 – Superconduttività
in
quantum
physics:
8
Campo Magnetico
Il campo magnetico è uno dei parametri critici di un superconduttore. Esso è generato
da correnti elettriche macroscopiche, come quelle che possono circolare nei fili
conduttori, o microscopiche, come quelle associate agli elettroni sulle orbite atomiche;
può anche essere la naturale manifestazione di una particolare classe di materiali
chiamati ferromagnetici.
Vediamo qui di seguito la relazione tra le linee di forza del campo magnetico e quelle
delle correnti che possono generarlo, oltre a esempi di magneti naturali.
Nel caso di un filo percorso da corrente la 'regola della mano destra' fa al caso
nostro.
V. Augelli, Fisica degli Stati Condensati, Cap.12 – Superconduttività
9
La legge di Ampere ci permette di calcolare il campo magnetico generato da un filo
infinitamente lungo percorso da una corrente I, ad una distanza r dal filo.
µ0 I
2πr
B=
Una spira di filo conduttore crea un campo magnetico molto più concentrato al centro
che al di fuori della spira. Più spire insieme creano un solenoide.
La legge di Biot-Savart applicata al nostro sistema ci permette di conoscere il modulo
del campo magnetico in un qualsiasi punto dell'asse della spira (che ha raggio R ed è
percorsa dalla corrente I):
B=
µ0 R 2 I
(z
2
+ R2
)
3
La direzione e il verso ci sono dati dalla regola della mano destra.
Vediamo cosa accade in un superconduttore.
Le correnti che circolano all'interno del superconduttore generano un campo
magnetico molto forte tutt'intorno allo stesso. Quando un superconduttore è
raffreddato al di sotto della temperatura critica Tc , il campo magnetico è limitato
all'esterno del superconduttore. Se il campo magnetico esterno è portato al di sopra
di un valore critico Hc , il superconduttore passa allo stato normale. Questo valore del
campo magnetico ad una data temperatura è detto campo magnetico critico (Hc). Per
tutti i superconduttori esiste una regione di temperature critiche e campi magnetici
critici all'interno della quale superconducono.
Elemento
Tc [K] Bc [mT] Elemento
Tc [K] Bc [mT]
Hg (mercurio) 4.15
41.2
Zr (zirconio)
0.55
4.7
In (indio)
3.40
29.3
Ti (titanio)
0.39
10
La (lantanio)
6.00
110.0
Zn (zinco)
0.88
5.3
Nb (niobio)
9.50
198
Al (alluminio)
1.14
10.5
Pb (piombo)
7.19
80.3
Mo (molibdeno) 0.92
9.5
Re (renio)
1.40
19.8
Hf (afnio)
-
1.12
V. Augelli, Fisica degli Stati Condensati, Cap.12 – Superconduttività
10
Sn (stagno)
3.72
30.9
Ru (rutenio)
0.51
7
Ta (tantalio)
4.48
83.0
Cd (cadmio)
0.56
3
Tc (tecnezio)
7.77
141.0
Ga (gallio)
1.09
5.1
Th (torio)
1.37
16.2
W (tungsteno)
0.01
1.1
Tl (tallio)
2.39
17.2
Ir (iridio)
0.14
1.9
V (vanadio)
5.38
142.0
Os (osmio)
0.66
6.5
Effetto Meissner
Vediamo quali sono i concetti importanti per comprendere al meglio questa proprietà
della superconduttività. Un conduttore immerso in un campo magnetico esterno che
non induce cambiamenti nel campo magnetico stesso e che si oppone alla crescita del
campo al suo interno è detto diamagnetico.
Un superconduttore ha un comportamento perfettamente diamagnetico dopo essere
stato portato al di sotto della temperatura critica di transizione.
V. Augelli, Fisica degli Stati Condensati, Cap.12 – Superconduttività
11
L'effetto Meissner prevede l'espulsione del campo magnetico esterno dal volume
occupato dal superconduttore. Quando la temperatura si abbassa al di sotto della
temperatura critica Tc il superconduttore espelle il campo magnetico all'esterno. Ciò è
dovuto all’esistenza di supercorrenti di superficie che producono un campo magnetico
esattamente opposto a quello esterno e che ne impedisce la penetrazione. Il
superconduttore diventa perfettamente diamagnetico annullando completamente il
flusso magnetico al suo interno.
Parametri critici
Lo stato superconduttore è individuato da tre parametri fondamentali: la temperatura
critica Tc, il campo magnetico critico Hc, e la densità di corrente critica Jc. Ciascuno
di questi parametri è strettamente dipendente dagli altri due. Mantenere un
materiale nello stato di superconduzione significa fare in modo che le tre grandezze
siano tutte al di sotto del proprio valore critico, che dipende dal materiale.
V. Augelli, Fisica degli Stati Condensati, Cap.12 – Superconduttività
12
Densità di corrente
Jc
Regione di superconduzione
Tc
Temperatura
Hc
Campo magnetico
Considerando contemporaneamente i tre parametri, si definisce una superficie che
raggruppa i valori degli stati superconduttori al suo interno.
Temperatura critica, Tc
La coppia di Cooper (si veda teoria BCS) rimane stabile tutto il tempo in cui il
superconduttore è raffreddato a temperature molto basse. Non appena il
superconduttore riceve energia termica le vibrazioni del reticolo diventano maggiori e
tanto grandi da rompere le coppie. Il superconduttore passa così allo stato di
conduttore normale. I composti e i metalli superconduttori hanno temperature
caratteristiche proprie di transizione tra i due stati (normale e superconduttore):
tale temperatura è indicata come temperatura critica o temperatura di transizione. Al
di sotto di questa, la resistività è nulla, al di sopra segue le normali leggi.
Vediamo nelle tabelle seguenti le temperature critiche di alcuni composti e di alcuni
metalli superconduttori.
Composto Tc [K] Composto
Tc [K]
NbTi
9.2
BaPb0.75Bi0.25O3
11
Nb3Al
18.8
UBe13
0.75
V3Ga
15
Pb0.7Bi0.3
8.45
PbMo6S8 14
V3Si
1.71
Nb3Sn
(SN)x
0.26
18.05
V. Augelli, Fisica degli Stati Condensati, Cap.12 – Superconduttività
13
Nb3Ge
22.3
(BEDT)2Cu(NCS)2 10
NbN
16
La1.8Sr0.2CuO4
38
NbO
1.2
Bi2CaSr2Cu2O8+X
90
Elemento
Tc[K]
Hg (mercurio)
4.15
La (lantanio)
4.9
Pa (protoattinio) 1.4
Re (renio)
1.698
Ru (rutenio)
0.49
Tl (tallio)
2.39
U (uranio)
0.68
Tl (tallio)
2.39
V (vanadio)
5.30
Densità di corrente critica, Jc
Questo valore indica la massima quantità di corrente trasportabile da un
superconduttore. Quando un superconduttore trasporta corrente non ci sono perdite
di energia elettrica e si può pensare quindi di poter trasportare quantità enormi di
corrente. In realtà un valore di corrente al di sopra di quello critico fa passare il
superconduttore ad uno stato normale anche se al di sotto della temperatura critica.
La densità di corrente critica Jc è una funzione della temperatura.
Campo magnetico critico, Hc
Questo parametro indica il valore massimo del campo magnetico sostenibile da un
superconduttore. I superconduttori di II tipo hanno due valori critici del campo
magnetico; questi valori individuano in un diagramma di fase magnetica tre zone con
diverso comportamento.
V. Augelli, Fisica degli Stati Condensati, Cap.12 – Superconduttività
14
Superconduttori di I e II tipo
Le classi di superconduttori di tipo I e tipo II si possono distinguere facendo
riferimento a due importanti scale microscopiche di lunghezza: la lunghezza di
coerenza e la lunghezza di penetrazione.
La lunghezza di coerenza è la separazione spaziale degli elettroni all'interno di una
coppia di Cooper, cioè le dimensioni medie della coppia. Nei superconduttori
convenzionali, la lunghezza di coerenza può andare da alcune decine ad alcune
centinaia di nanometri. La lunghezza di penetrazione è relativa all'effetto Meissner.
Le correnti indotte che creano il campo magnetico che si oppone a quello esterno
applicato, cancellandolo dall'intero materiale, decadono esponenzialmente in intensità
all'aumentare della distanza dalla superficie del superconduttore. La distanza lungo la
quale avviene questo decadimento è proprio la lunghezza di penetrazione: questa è la
distanza più breve lungo la quale un campo magnetico può variare in un
superconduttore. Nei superconduttori convenzionali essa può andare da qualche decina
fino a qualche migliaio di nanometri. Queste lunghezze microscopiche definiscono due
classi molto diverse di superconduttori. Nei superconduttori di I tipo la lunghezza di
coerenza è maggiore della lunghezza di penetrazione. Questi materiali tendono ad
essere superconduttori in condizioni di bassa temperatura e debole campo magnetico;
se il campo raggiunge l'intensità critica (la quale varia da materiale a materiale), il
campo stesso entra nel volume del materiale distruggendo lo stato superconduttivo.
Poiché nei superconduttori di tipo I, la superconduzione scompare in presenza di campi
magnetici di intensità relativamente bassa, questi materiali presentano uno scarso
interesse dal punto di vista tecnologico. Questa classe di superconduttori è ben
descritta dalla teoria BCS (Bardeen, Cooper, Schrieffer). Ci sono 30 metalli puri che
appartengono a questa classe: ne sono un esempio il piombo, il mercurio, lo stagno. Il
superconduttore più 'forte' del I tipo ha un campo critico di 800 G (gauss).
V. Augelli, Fisica degli Stati Condensati, Cap.12 – Superconduttività
15
Ricordiamo che il campo magnetico terrestre è di 0.5 G. Il mercurio è stato il primo
metallo a 'mostrarsi' superconduttore. Il valore del suo campo critico è pari a 0.019 T
(190 G) così che la quantità di corrente elettrica trasportabile risulta limitata. La sua
temperatura critica ha lo storico valore di 4.2 K
I superconduttori di II tipo sono molto più utili per le applicazioni. La profondità di
penetrazione in questi materiali è maggiore della lunghezza di coerenza e rimangono
nello stato di superconduzione anche dopo la penetrazione del campo magnetico. I
superconduttori di II tipo possono sopportare campi molto forti - fino a quello che è
chiamato campo critico superiore - e quindi trasportare correnti più intense. Questa
classe di superconduttori è stata identificata a partire dal 1930 con i composti di
piombo-bismuto. Tutti i superconduttori di interesse tecnologico, inclusi quelli ad alta
temperatura critica finora noti, sono di questo tipo. L'YBaCuO e lo BiSrCaCuO sono
esempi di superconduttori del II tipo. Un valore indicativo del campo magnetico alla
superficie di questi superconduttori è approssimativamente di 16000 G (corrisponde a
quello del neodimio-ferro-boro). Questo materiale ceramico è stato il primo dei
superconduttori ad alta temperatura ad essere stato studiato. La sua temperatura
critica è pari al valore (anch'esso storico) di 35 K. E' costituito da un reticolo di
ossido di rame-lantanio in cui sono presenti in modo random atomi di bario. Questo
materiale ceramico è stato il primo ad essere sintetizzato con una temperatura
critica superiore a quella di liquefazione dell'azoto (77 K).
V. Augelli, Fisica degli Stati Condensati, Cap.12 – Superconduttività
16
Berdnorz e Mueller hanno studiato
struttura senza Sr)
il La2-xSrxCuO2 (in figura è rappresentata la
Primo materiale a superare i 77 K (YBCO).
V. Augelli, Fisica degli Stati Condensati, Cap.12 – Superconduttività
17
Teoria microscopica BCS
Nel 1957 John Bardeen, Leon N. Cooper e J. Robert Schrieffer misero a punto una
teoria capace di spiegare il fenomeno della superconduzione nei metalli che la
mostrano a bassa temperature. In tali materiali, gli elettroni di conduzione si
propagano senza incontrare resistenza perché si muovono in coppie (coppie di Cooper).
Gli elettroni formano coppie di Cooper in quanto interagiscono in modo dinamico con i
fononi.
I fononi tendono a neutralizzare la repulsione coulombiana, che normalmente si
esercita tra gli elettroni, producendo una debole forza attrattiva che lega gli
elettroni in coppie.
Un elettrone che passa, attrae il reticolo causandone una deformazione; un secondo
elettrone viene a sua volta attratto dalla regione deformata per cui si crea la coppia.
Gli ioni (cariche positive) sono attirati a causa dell'interazione coulombiana verso un
elettrone di conduzione (carica negativa) che si muove attraverso il reticolo del solido,
creando così una regione arricchita di carica positiva. Questa regione del reticolo
attira a sua volta un altro elettrone che si trova nelle vicinanze.
Il legame risultante tra i due elettroni è debole, con un'energia tipica di pochi meV,
che è però sufficiente ad impedire che la coppia venga divisa a causa degli ostacoli
della normale conduzione. Di conseguenza, le coppie di Cooper si propagano nel
materiale senza incontrare resistenza. L'intensità di questa interazione dipende
V. Augelli, Fisica degli Stati Condensati, Cap.12 – Superconduttività
18
fortemente dalla temperatura essendo il raffreddamento essenziale per bloccare le
vibrazioni reticolari (i fononi). A temperature al di sopra del valore critico, le
fluttuazioni termiche distruggono le coppie di Cooper e di conseguenza lo stato di
superconduzione del metallo.
Un'utile analogia interpretativa è rappresentata da un sistema di due palline (gli
elettroni) che si trovino su un tappeto morbido di gomma (il reticolo).
Se queste palline sono lontane l'una dall'altra ognuna indipendentemente deforma il
tappetino creando una concavità attorno a sé. Se le mettiamo non troppo lontane l'una
dall'altra si può osservare che le concavità così createsi si uniscono in una sola e le
palline si portano sul fondo della comune concavità.
Le dimensioni di queste coppie
possono raggiungere centinaia ed anche migliaia di distanze interatomiche. Per questo
sarebbe meglio pensarle non come coppie di elettroni legati l'un l'altro, come una
stella binaria, ma piuttosto come propose P. Schrieffer, alla stregua di un ragazzo ed
una ragazza che vanno insieme in discoteca ma ballano in diverse parti della sala,
separati da centinaia di altri danzatori. È bene rilevare che la coppia di Cooper è una
struttura dinamica cioè esiste solo in moto. Consideriamo un elettrone in moto lungo
un canale del reticolo cristallino alla velocità di Fermi, vF ~ 108 cm/sec. Ad un certo
istante, quando l'elettrone si trova tra due ioni vicini, questi subiscono un breve
impulso dovuto all'attrazione coulombiana con l'elettrone stesso. La durata di questo
impulso è all'incirca il tempo di transito dell'elettrone tra due ioni vicini e quindi pari a
τ =
a
= 10−16 s
vF
V. Augelli, Fisica degli Stati Condensati, Cap.12 – Superconduttività
19
con a distanza interatomica (10-8 cm). Durante questo intervallo di tempo gli ioni, che
hanno una frequenza di vibrazione propria ω tipicamente dell'ordine di 1013 Hz, non
cambiano praticamente posizione. Dopo mezzo periodo di vibrazione gli ioni si portano
ad una distanza minima e in questa configurazione si crea nel reticolo cristallino un
aumento locale di densità di carica positiva. A questo istante, l'elettrone che ha
creato tale aumento di carica, si trova già lontano, avendo percorso una distanza pari a
d≅
vF
ω
= 10− 4 cm
molto più grande del parametro reticolare a. La nuvola di carica positiva in eccesso
segue quindi come una scia l'elettrone, che passa tra gli ioni con velocità vF . Questa
'nuvola' positiva può attrarre un secondo elettrone, che peraltro si trova più vicino
alla nuvola stessa che non al primo elettrone. Gli elettroni, dinamicamente collegati
attraverso la nuvola di carica positiva, costituiscono le coppie di Cooper la cui
dimensione è pari appunto a 10-4-10-5 cm. Ecco perchè le coppie di Cooper appaiono
molto più 'lunghe' del passo reticolare.
TEORIA MATEMATICA
TEMPERATURA DI TRANSIZIONE
Un metallo o comunque un materiale che normalmente è un conduttore,
quando viene portato a temperature via via inferiori, offre una resistenza
sempre minore al passaggio di corrente. Si è osservato che alcuni materiali,
al di sotto di una certa temperatura, mantengono una resistenza quasi
costante. In altri invece, in corrispondenza di un determinato calo di
temperatura, si è osservata una improvvisa caduta della resistenza
(temperatura di transizione).
V. Augelli, Fisica degli Stati Condensati, Cap.12 – Superconduttività
20
Resistenza in funzione della temperatura
per un conduttore e per un superconduttore
I primi tentativi per spiegare questo fenomeno furono formulati da Fröhlich
nel 1950. Egli per primo considerò le possibili interazioni tra gli elettroni e il
reticolo cristallino. Infatti l’interazione tra gli elettroni è mediata dai fononi
ed è questo tipo d’interazione che dà luogo alla superconduttività. Nei
metalli nobili (oro, argento, rame) gli elettroni interagiscono poco con il
reticolo e questo è il motivo per cui non diventano superconduttori. Fröhlich
trovò una relazione tra la temperatura di transizione e i vari isotopi di uno
stesso elemento (effetto isotopico):
con α variabile tra - 0,5 e + 2 e M, la massa dell’isotopo.
La Tc dipende fortemente anche dalla pressione (in maniera inversamente
proporzionale), dallo spessore e dalla carica elettrica del campione in esame.
RESISTENZA ELETTRICA
La resistenza elettrica in un normale conduttore è causata principalmente
dallo scattering degli elettroni, che vengono rallentati nel loro cammino. I
meccanismi predominanti sono: fonone - elettrone e elettrone - elettrone.
Questi danno un contributo alla resistività totale che chiameremo ρ(T)
(resistività intrinseca). Tuttavia esistono anche altri ostacoli al moto degli
elettroni. Un reticolo cristallino non è mai perfetto,ci sono difetti di vario
genere che rallentano il moto degli elettroni. Conseguentemente anche
V. Augelli, Fisica degli Stati Condensati, Cap.12 – Superconduttività
21
questo darà un contributo alla resistività totale. Allora la resistività totale
del materiale si può scrivere come:
nota come legge di Mattheissen.
Il termine ρi generalmente non dipende dalla temperatura, mentre la ρ(T)
può dipendere anche fortemente dalla temperatura. Se consideriamo un gas
di elettroni, la sua resistività sarà data da (legge di Drude):
Ora in un cristallo dove la T →0 si avrà una progressiva diminuzione dell'agitazione
termica, quindi una diminuzione di fononi. Allora il tempo medio tra due urti tenderà a
infinito, quindi si può supporre che:
CORRENTE PERSISTENTE
In un esperimento, Onnes indusse una corrente in un anello di materiale
superconduttore utilizzando un campo magnetico.
Schema dell'esperimento di Onnes
V. Augelli, Fisica degli Stati Condensati, Cap.12 – Superconduttività
22
Usando la legge di Lenz
dove: B = densità di flusso magnetico, R = resistenza dell'anello, L =
induttanza dell'anello, A = area racchiusa nell'anello. Se togliamo il campo
magnetico
e quindi
Se considero un materiale superconduttore avente R = 0, ottengo:
I (t) = I (t = 0)
cioè, in un materiale superconduttore, una volta indotta una corrente, anche
se si toglie il campo, la corrente continua a fluire per un tempo teoricamante
infinito. In realtà, c'è comunque una resistività residua. Nel caso in cui si
abbia una ρ= 10-23 Ω·cm si può calcolare il tempo necessario perchè la
corrente smetta di fluire nell'anello, che risulta superiore a 1010 anni.
EFFETTO MEISSNER
Se in un superconduttore il campo elettrico fosse diverso da zero, avremmo
una corrente infinita essendo la sua resistenza nulla. Perciò, essendo
r
r
r
1 ∂B
∂B
rotE = −
= 0 . Ciò significa che se raffreddiamo in
, dev’essere
c ∂t
∂t
assenza di campo magnetico fino a sotto la temperatura critica il campo
magnetico resterà nullo, ma se raffreddiamo in presenza di campo
magnetico, questo sarà diverso da zero anche al di sotto della temperatura
critica e ciò è contro l’evidenza sperimentale (effetto Meissner) che vuole
B=0 e E=0. Affinché si annulli il campo magnetico quando scendiamo al di
sotto della temperatura critica, è necessario che esista un campo elettrico
transitorio che generi una corrente non dissipativi che crei una
magnetizzazione M tale che B = H + 4πM = 0. La corrente dovrà quindi
V. Augelli, Fisica degli Stati Condensati, Cap.12 – Superconduttività
23
generare una polarizzazione diamagnetica M = - H/4π = χH, essendo χ la
suscettività diamagnetica.
Se supponiamo che una certa frazione, ns/n, di elettroni contribuisce alla
supercorrente, la densità di corrente sarà data da:
Se supponiamo che esista un campo elettrico transitorio, si avrà
e quindi
Prendendo il rotore di entrambi i membri e usando la legge di Maxwell
si ottiene
V. Augelli, Fisica degli Stati Condensati, Cap.12 – Superconduttività
24
Posso poi ancora legare B e J dalla relazione
Usando quindi l'identità vettoriale
otteniamo
Risulta chiaro che ogni campo B indipendentemente dal tempo soddisferà
questa equazione. Quindi se inizialmente il campo applicato è nullo, allora
anche in un secondo momento il campo interno sarà nullo. Ma la relazione
precedente è soddisfatta per qualunque coppia di soluzioni statiche di J e B
e quindi l’effetto Meissner non si spiega.
TEORIA DI LONDON
I fratelli London trovarono una spiegazione all'effetto Meissner. Essi
supposero che non solo la derivata
è nulla, ma è nullo anche la funzione, ovvero
la lunghezza di penetrazione. Una relazione
essendo
simile può essere scritta anche per J:
r 1 r
∇ j= 2 j
2
λ
V. Augelli, Fisica degli Stati Condensati, Cap.12 – Superconduttività
25
Una soluzione per questa equazione dipende dalle caratteristiche
geometriche del provino e dalle condizioni al contorno. Generalmente, per la
maggior parte dei superconduttore, si ottiene λL = 500 Å.
Il campo esterno penetra all'interno del superconduttore per un breve
tratto ma decade esponenzialmente, infatti:
A causa di questo piccolo campo si forma una corrente nel bordo
superconduttore che viene chiamata screening current. La lunghezza di
penetrazione dipende dalla temperatura, infatti quando T diventa maggiore
di Tc allora ns si annulla e λ diventa infinito cioè il campo magnetico
penetrerà uniformemente nel materiale.
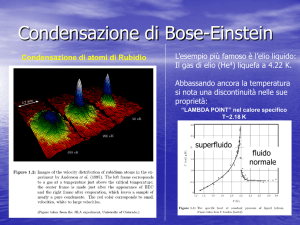
Calore specifico.
In un superconduttore esiste un gap di energia nello spettro di eccitazione
degli elettroni. Questo gap di energia fu scoperto facendo misure di calore
specifico. In un normale metallo il calore specifico a bassa temperatura è
dato da
C = T + BT3
dove il termine lineare è dovuto alla eccitazione degli elettroni, mentre
quello cubico deriva dalla eccitazione dei fononi. Come si può osservare in
figura, alla temperatura critica la capacità termica ha un brusco aumento e
successivamente decresce con la temperatura. Se usiamo un campo
magnetico che distrugge lo stato superconduttore e siamo sotto la
temperatura critica, il calore specifico riprende l’andamento lineare che
aveva nello stato normale.
V. Augelli, Fisica degli Stati Condensati, Cap.12 – Superconduttività
26
Lavorando a temperature maggiori della temperatura critica Tc il contributo
degli elettroni ha la forma
che è caratteristico di un sistema con un gap di energia nello spettro di
eccitazione.
Predizioni della teoria BCS.
BCS considerarono un gas di Fermi nello stato fondamentale e studiarono
l’equazione di Schroedinger per una coppia di elettroni di spin opposti. Le
predizioni più importanti della teoria furono:
a 0 K:
V. Augelli, Fisica degli Stati Condensati, Cap.12 – Superconduttività
27
essendo NF la densità degli stati al livello di Fermi, F il potenziale di
interazione effettivo, hω D ≈ kθ D (energia di Debye per i fononi).
Aumentando la temperatura il gap di energia diminuisce, e tende a zero
quando T tende a Tc. In prossimità della temperatura critica vale la formula
Contemporaneamente il campo magnetico critico ha un andamento del tipo
dove a è una costante che è poco sensibile alle variazioni di temperatura.
Anche la capacità termica dipende dal gap di energia, secondo la relazione
La differenza rispetto ad uno stato normale è data da:
La teoria BCS permette di calcolare in anticipo la Tc usando i parametri
usati fin qui:
Anche il gap a 0 K si può usare per il calcolo di Tc:
V. Augelli, Fisica degli Stati Condensati, Cap.12 – Superconduttività
28